Type Systems
This section deals with more theoretical aspects of types.
A type system is a set of rules used by a language to structure and organize its collection of types.
We use the term object (or data object) to denote both the storage and the stored value.
The operations defined for a type are the only way to manipulate its instantiated objects.
A type error is any attempt to manipulate objects with illegal operations.
A program is type safe (or type secure) if it is guaranteed to have no type errors.
Static Versus Dynamic Program Checking ( for type errors )
Let's consider errors in general before looking at type errors specifically.
- What kinds of errors may occur in programs?
- When may errors be checked for?
- How does error-checking time affect the quality of the resulting programs?
There are two categories of errors
- Language errors - syntactic and semantic errors in the use of the PL
- Application errors - deviations in program behavior relative to the program's specifications
- has to do with software design issues, which are outside the scope of this book
There are two broad categories of error checking based on when the errors are checked for
- dynamic error checking - requires the program to be executed on sample input data
- static error checking - does not require program execution
- Preferable to dynamic checking
- potential errors are only detected at runtime if the input data we provide causes the error
- dynamic checking slows down program execution
- Often called compile-time checking or translation-time checking
- a misnomer since with separate compilation some checks must be made at link time
- a misnomer since with separate compilation some checks must be made at link time
- Does not uncover all errors. Some are only manifest at run time
- Preferable to dynamic checking
Strong Typing and Type Checking
The goal of a type system is to prevent the writing of type-unsafe programs as much as possible.
- A type system is said to be strong, if it guarantees type safety.
- A type system is said to be weak if it is not strong.
- A strongly typed language is one with a strong type system.
- A weakly typed language is one with a weak type system.
In general, there different ways for a PL to achieve a strong type system.
- A statically typed language is a strongly typed language
- Example: A static type system can be achieved by requiring:
- Only built-in types can be used
- All variables are declared with an associated type
- All operations are specified by stating the types of the required operands and the type of the result
- In some languages the binding between a variable and its type cannot be determined
at compile-time, yet their type systems guarantee type safety
How should a designer choose a type system when designing a new PL?
- Two conflicting design specifications
- The size of the set of legal programs
- The efficiency of the type checking procedure in the compiler
- The type system restricts the set of programs that can be written
- A smaller set of programs � simpler type checking
Type Compatibility
Consider a PL with an operation, OP, which expects an operand of type T
A strict type system might require that OP may only be legally invoked with a parameter of type T
On the other hand, the PL might define conditions under which an operand of type Q is also acceptable
without violating type safety.
In this case we say that "in the context of operation OP, type Q is compatible with type T".
Type compatibility is sometimes called type conformance or type equivalence.
When this compatibility is precisely defined, the PL can still have a strong type system.
Example: The program fragment in figure 3.8 is written in a hypothetical PL.
What are the effects of different sorts of type compatibility rules?

Name Compatibility - A strict conformance rule in which a type name is compatible only with itself
Under this rule:
- (2) is type correct
- (1), (3) and (4) contain type errors
Structural Compatibility - Two types are compatible if they have the same structure
Under this rule:
- (1),(2) and (3) are type correct
- (4) contains a type error
A few issues with structural compatibility as defined here.
- What happens with the field names of Cartesian Products?
- Ignored? Required to coincide? Required to occur in same order?
Name Compatibility is:
- easier to implement than structural compatibility
- much stronger than structural compatibility
Name compatibility is often preferable because it prevents two types from being considered
compatible just because their representations happen to be identical.
Practical Issue:
Some PLs adopt the idea of type compatibility, but either poorly define the rules
or leave it entirely up to the implementer.
This results in programs accepted by one compiler and rejected by another compiler
Type Conversions
- Automatic conversions , called coercions
- Explicit conversions, called casts

Example of coercion
x = x + z; (in C )
Any coercions which may occur depend on context.
If z is float and x is int:
- x is coerced to float to evaluate the addition, which is a real addition
- the result is coerced to an int for the asignment
Explicit Type Conversion
An explicit conversion can be used in some PLs to avoid an undesirable coercion.
For example, C has a cast construct which can force a type conversion that otherwise
might not occcur.
Assuming the same variable types as above, a programmer could write:
x = x + (int) z;
- z is coerced to type int
semantically, z is assigned to an unamed variable of
type int using the normal coercion rules
- the un-named variable is used to evaluate the addition, which is integer
Ada provides only explicit conversions, subject to rules defining allowed conversions.
- If X is declared as FLOAT and I as INTEGER
I := INTEGER(X);
The conversion function, INTEGER(), provided by Ada, is
applied to X to give the nearest INTEGER.
Advantages of allowing coercions
- Desirable conversions are automatically done
Disadvantages of allowing coercions
- These implicit conversions are 'behind the scenes'
� PL gets complicated
� Programs may become obscure
- Coercions weaken the usefulness of type checking by overriding the declared types of objects
The interaction between coercions and overloading of operators and routines makes programs
difficult to understand.
Types and Subtypes
Assume a type T is defined as a set of values with an associated set of operations.
A subtype STof T can be defined to be a subset of those values ( and, for simplicitiy, the same operations )
*note - the discussion here is in the context of conventional PLs. We ignore the ability to
specify user-defined operations for subtypes
If ST is a subtype of T, T is also called ST's supertype (or parent type)
If a PL supports subtypes, it must define:
- A way to define subsets of a given type
- Compatibility rules between a subtype and it's supertype
Example - Pascal
- introduced concept of subtype as a subrange of any discrete ordinal type
type natural = 0..maxint;
digit = 0..9;
small = -9..9;
- A Pascal program may only define a subset of contiguous values
- e.g. a subtype of all even integers would not be allowwed
- Different subtypes of a given type are compatible among themselves and the supertype,
but type-safe operations may cause run-rime errors.
- e.g. small is provided to an expression requiring a digit may cause error
Generic Types
Consider a generic abstract data type for a stack of elements of parameter type T,
with operations having the following signatures:
push: stack(T) � T � stack(T)
pop: stack(T) � stack(T) � T
length: stack(T) �int
The operations defined for type stack(T) should work uniformly for any possible type T.
Since the type is not known, how can the routines be type-checked?
PLs like Ada, C++ and Eiffel support this by instantiating generic types and/or routines at compile-time.
The generic type parameters are bound to concrete types, enabling type-checking.
- C++ only requires explicit instantiation of generic classes, not routines
Monomorphic versus Polymorphic Type Systems
A statically typed language can provide a strong, simple type system in which every program entity
has a specific type (defined by a declaration), and every operation requires operands of exactly
the sort appearing in the operation definition.
A monomorphic type system is a type system in which every object belongs to one and only one type,
as described above.
A polymorphic type system is a type system in which objects can belong to more than one type.
C, Pascal and Ada all deviate from strict monomorphism to some degree.
- compatibility
- coercion
- subtyping
- operator overloading
All practical PLs have some degree of polymorphism, so to differentiate between them
we need to differentiate among the various levels and kinds of polymorphism.
The different facets of polymorphism can be classifies as shown in figure 3.10.
Let's show how the classification scheme applies in the case of polymorphic functions.
Polymorphic functions are those whose arguments and return values (domain and range)
can belong to more than one type.
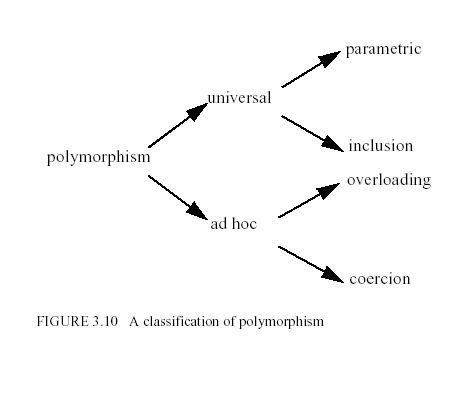
Level 1 - universal vs, ad hoc polymorphism
- functions that are universally polymorphic work uniformly for an infinite set of types
all of which have some common structure
- execute the same code for all admissible types
- execute the same code for all admissible types
- An ad hoc polymorphic function is just a syntactic abbreviation for small set of
different monomorphic functions.
Level 2 - universal :: parametric vs inclusion
- parametric polymorphism is the most genuine form of universal polymorphism.
- in this case the polymorphic function works uniformly on a range of types
- an implicit or explicit type parameter determines the type of arguments for each use
- generic routines as implemented by ML functions are an example of this
- generic routines as implemented in Ada and C++ are only an apparent kind of polymorphism
- they can be viewed as ad hoc polymorphism since the routines are instantiated at compile time
with full binding of parameters to specific types.
- they can be viewed as ad hoc polymorphism since the routines are instantiated at compile time
- an example of inclusion polymorphism is subtyping
- the function is applicable to a given type and any of its subtypes
- also applicable in the context of object oriented languages
- dynamic polymorphism is frequently used to classify the case where the binding between
language entities and their form varies dynamically.
PLs which support this cannot have strong type systems
Level 2 - ad hoc :: overloading vs. coercion
- In overloading, the same function name can be used in different contexts to denote different functions
- Example in C : arithmetic expression a + b
+ is an ad hoc polymorphic function whose behavior depends on its operand types
- float operands machine instruction float+
- int operands machine instruction int+
The fact that + is overloaded is purely a syntactic phenomenon
- Example in C : arithmetic expression a + b
- In coercion, the argument is converted to a type expected by the function
- the polymorphism is only apparent
- provided statically by code inserted by the compiler
- provided dynamically by runtime tests on type descriptors
- Example in C : arithmetic expression a + b
+ is an ad hoc polymorphic function whose behavior depends on its operand types as above
If the two operands are different types, the float+ operator is invoked after coercing the int
operand to a real.
- the polymorphism is only apparent
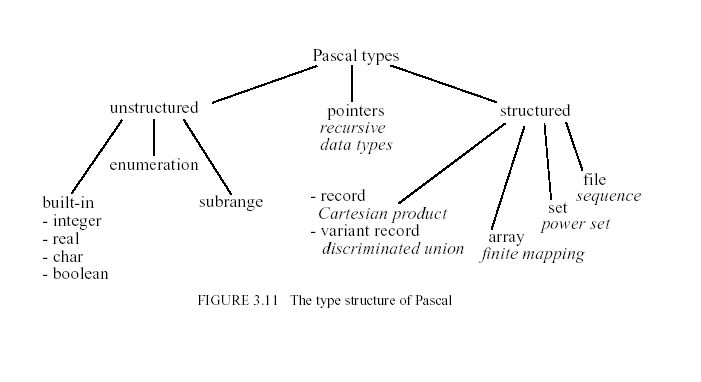
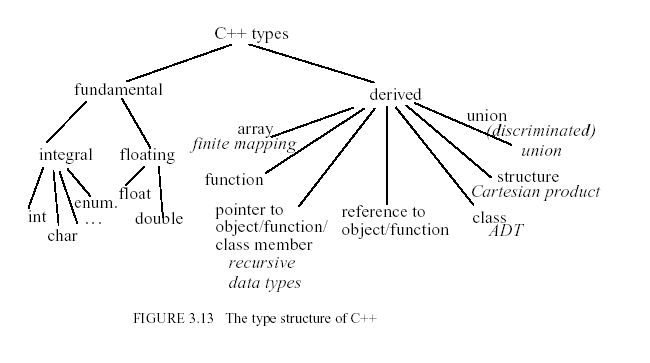
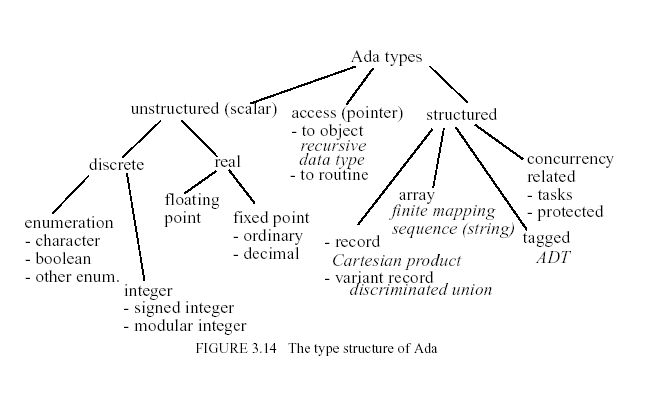
The Type Structure of Representative Languages
The type structure of a PL is an overall hierarchical classification of the features provided for structuring data.
In order to completely understand the semantics of a PL, this description must be complemented by a precise
understanding of the rules of the type system
http://www.cs.kent.edu/~durand/CS43101Fall2004/DT-TypeSystems.html



