第3章：LeetCode--算法：strStr KMP算法

https://leetcode.com/problems/implement-strstr/  28. Implement strStr()

暴力算法：

int ViolentMatch(char* s, char* p)  
{  
    int sLen = strlen(s);  
    int pLen = strlen(p);  
  
    int i = 0;  
    int j = 0;  
    while (i < sLen && j < pLen)  
    {  
        if (s[i] == p[j])  
        {  
            //①如果当前字符匹配成功（即S[i] == P[j]），则i++，j++      
            i++;  
            j++;  
        }  
        else  
        {  
            //②如果失配（即S[i]! = P[j]），令i = i - (j - 1)，j = 0      
            i = i - j + 1;  
            j = 0;  
        }  
    }  
    //匹配成功，返回模式串p在文本串s中的位置，否则返回-1  
    if (j == pLen)  
        return i - j;  
    else  
        return -1;  
}  

 

KMP(Knuth-Morris-Pratt)算法：

当T[i] != P[j]时

有T[i-j ~ i-1] == P[0 ~ j-1]

由P[0 ~ k-1] == P[j-k ~ j-1]

必然：T[i-k ~ i-1] == P[0 ~ k-1] -->because k<j

 如果给定的模式串是：“ABCDABD”，从左至右遍历整个模式串，其各个子串的前缀后缀分别如下表格所示：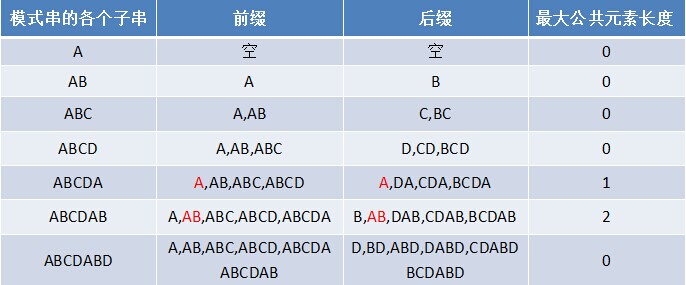

    也就是说，原模式串子串对应的各个前缀后缀的公共元素的最大长度表为（下简称《最大长度表》）：

 

KMP 算法：=NEXT数组下标从0开始更容易理解=

class Solution {
public:
     
    void GenNext(string p, int next[]){
        int plen = p.size();
        next[0] = 0;
        int j = 0;
        for(int i=1; i<plen; ){
            if(p[j] == p[i]){
                next[i] = j+1;
                j++;
                i++;
            }
            else{
                if(j!=0)
                    j = next[j-1];
                else{
                    next[i] = 0;
                    i++;
                }
            }
        }
    }
    int strStr(string haystack, string needle) {
        int slen = haystack.size();
        int plen = needle.size();
        if(slen < plen) return -1;
        if(needle == "" ||haystack == "") return 0;
        int i=0, j=0;
        int next[plen];
        GenNext(needle, next);
        while(i<slen && j<plen){
            if(haystack[i]==needle[j]){
                i++;
                j++;
            }else{
                if(j!=0)
                    j = next[j-1];
                else
                    i++;
            }
        }
        if(j==plen) return i-j;
        return -1;
    }
};

 KMP算法参考：https://www.cnblogs.com/ZuoAndFutureGirl/p/9028287.html

 

更高级搜索算法：

BM算法  Sunday算法https://www.cnblogs.com/ZuoAndFutureGirl/p/9028287.html