哈希函数与哈希冲突
什么是 Hash
Hash(哈希),又称“散列”。在某种程度上,散列是与排序相反的一种操作,排序是将集合中的元素按照某种方式比如字典顺序排列在一起。而散列通过计算哈希值,打破元素之间原有的关系,使集合中的元素按照散列函数的分类进行排列。
在介绍一些集合时,我们总强调需要重写某个类的 equlas() 方法和 hashCode() 方法,确保唯一性。这里的 hashCode() 表示的是对当前对象的唯一标示。计算 hashCode 的过程就称作 哈希。
为什么要有 Hash
我们通常使用数组或者链表来存储元素,一旦存储的内容数量特别多,需要占用很大的空间,而且在查找某个元素是否存在的过程中,数组和链表都需要挨个循环比较,而通过 哈希 计算,可以大大减少比较次数。
举个栗子: 现在有 4 个数 {2,5,9,13},需要查找 13 是否存在。
1.使用数组存储,需要新建个数组 new int[]{2,5,9,13},然后需要写个循环遍历查找:
int[] numbers = new int[]{2,5,9,13}; for (int i = 0; i < numbers.length; i++) { if (numbers[i] == 13){ System.out.println("find it!"); return; } }
这样需要遍历 4 次才能找到,时间复杂度为 O(n)。
2.而假如存储时先使用哈希函数进行计算,这里我随便用个函数:
H[key] = key % 3;
四个数 {2,5,9,13} 对应的哈希值为:
H[2] = 2 % 3 = 2; H[5] = 5 % 3 = 2; H[9] = 9 % 3 = 0; H[13] = 13 % 3 = 1;
然后把它们存储到对应的位置。
当要查找 13 时,只要先使用哈希函数计算它的位置,然后去那个位置查看是否存在就好了,本例中只需查找一次,时间复杂度为 O(1)。
因此可以发现,哈希 其实是随机存储的一种优化,先进行分类,然后查找时按照这个对象的分类去找。
哈希通过一次计算大幅度缩小查找范围,自然比从全部数据里查找速度要快。
哈希函数
哈希的过程中需要使用哈希函数进行计算。
哈希函数是一种映射关系,根据数据的关键词 key ,通过一定的函数关系,计算出该元素存储位置的函数。
表示为:
address = H [key]
几种常见的哈希函数(散列函数)构造方法
- 直接定址法
- 取关键字或关键字的某个线性函数值为散列地址。
- 即 H(key) = key 或 H(key) = a*key + b,其中a和b为常数。
- 除留余数法
- 取关键字被某个不大于散列表长度 m 的数 p 求余,得到的作为散列地址。
- 即 H(key) = key % p, p < m。
- 数字分析法
- 当关键字的位数大于地址的位数,对关键字的各位分布进行分析,选出分布均匀的任意几位作为散列地址。
- 仅适用于所有关键字都已知的情况下,根据实际应用确定要选取的部分,尽量避免发生冲突。
- 平方取中法
- 先计算出关键字值的平方,然后取平方值中间几位作为散列地址。
- 随机分布的关键字,得到的散列地址也是随机分布的。
- 折叠法(叠加法)
- 将关键字分为位数相同的几部分,然后取这几部分的叠加和(舍去进位)作为散列地址。
- 用于关键字位数较多,并且关键字中每一位上数字分布大致均匀。
- 随机数法
- 选择一个随机函数,把关键字的随机函数值作为它的哈希值。
- 通常当关键字的长度不等时用这种方法。
构造哈希函数的方法很多,实际工作中要根据不同的情况选择合适的方法,总的原则是尽可能少的产生冲突。
通常考虑的因素有关键字的长度和分布情况、哈希值的范围等。
如:当关键字是整数类型时就可以用除留余数法;如果关键字是小数类型,选择随机数法会比较好。
哈希冲突的解决
选用哈希函数计算哈希值时,可能不同的 key 会得到相同的结果,一个地址怎么存放多个数据呢?这就是冲突。
常用的主要有两种方法解决冲突:
1.链接法(拉链法)
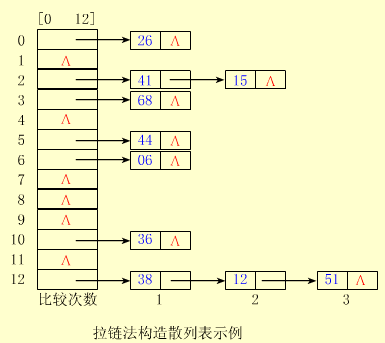
拉链法解决冲突的做法是:
将所有关键字为同义词的结点链接在同一个单链表中。
若选定的散列表长度为 m,则可将散列表定义为一个由 m 个头指针组成的指针数组 T[0..m-1] 。
凡是散列地址为 i 的结点,均插入到以 T[i] 为头指针的单链表中。
T 中各分量的初值均应为空指针。
在拉链法中,装填因子 α 可以大于 1,但一般均取 α ≤ 1。
2.开放定址法
用开放定址法解决冲突的做法是:
用开放定址法解决冲突的做法是:当冲突发生时,使用某种探测技术在散列表中形成一个探测序列。沿此序列逐个单元地查找,直到找到给定的关键字,或者碰到一个开放的地址(即该地址单元为空)为止(若要插入,在探查到开放的地址,则可将待插入的新结点存人该地址单元)。查找时探测到开放的地址则表明表中无待查的关键字,即查找失败。
简单的说:当冲突发生时,使用某种探查(亦称探测)技术在散列表中寻找下一个空的散列地址,只要散列表足够大,空的散列地址总能找到。
按照形成探查序列的方法不同,可将开放定址法区分为线性探查法、二次探查法、双重散列法等。
a.线性探查法
hi=(h(key)+i) % m ,0 ≤ i ≤ m-1
基本思想是:
探查时从地址 d 开始,首先探查 T[d],然后依次探查 T[d+1],…,直到 T[m-1],此后又循环到 T[0],T[1],…,直到探查到 有空余地址 或者到 T[d-1]为止。
b.二次探查法
hi=(h(key)+i*i) % m,0 ≤ i ≤ m-1
基本思想是:
探查时从地址 d 开始,首先探查 T[d],然后依次探查 T[d+1^2],T[d+2^2],T[d+3^2],…,等,直到探查到 有空余地址 或者到 T[d-1]为止。
缺点是无法探查到整个散列空间。
c.双重散列法
hi=(h(key)+i*h1(key)) % m,0 ≤ i ≤ m-1
基本思想是:
探查时从地址 d 开始,首先探查 T[d],然后依次探查 T[d+h1(d)], T[d + 2*h1(d)],…,等。
该方法使用了两个散列函数 h(key) 和 h1(key),故也称为双散列函数探查法。
定义 h1(key) 的方法较多,但无论采用什么方法定义,都必须使 h1(key) 的值和 m 互素,才能使发生冲突的同义词地址均匀地分布在整个表中,否则可能造成同义词地址的循环计算。
该方法是开放定址法中最好的方法之一。
哈希的应用
哈希表(散列表)
哈希表(hash table)是哈希函数最主要的应用。
哈希表是实现关联数组(associative array)的一种数据结构,广泛应用于实现数据的快速查找。
用哈希函数计算关键字的哈希值(hash value),通过哈希值这个索引就可以找到关键字的存储位置,即桶(bucket)。
哈希表不同于二叉树、栈、序列的数据结构一般情况下,在哈希表上的插入、查找、删除等操作的时间复杂度是 O(1)。
查找过程中,关键字的比较次数,取决于产生冲突的多少,产生的冲突少,查找效率就高,产生的冲突多,查找效率就低。
因此,影响产生冲突多少的因素,也就是影响查找效率的因素。
影响产生冲突多少有以下三个因素:
- 哈希函数是否均匀;
- 处理冲突的方法;
- 哈希表的加载因子。
哈希表的加载因子和容量决定了在什么时候桶数(存储位置)不够,需要重新哈希。
加载因子太大的话桶太多,遍历时效率变低;太大的话频繁 rehash,导致性能降低。
所以加载因子的大小需要结合时间和空间效率考虑。
在 HashMap 中的加载因子为 0.75,即四分之三。
分布式缓存
网络环境下的分布式缓存系统一般基于一致性哈希(Consistent hashing)。
简单的说,一致性哈希将哈希值取值空间组织成一个虚拟的环,各个服务器与数据关键字K使用相同的哈希函数映射到这个环上,数据会存储在它顺时针“游走”遇到的第一个服务器。可以使每个服务器节点的负载相对均衡,很大程度上避免资源的浪费。
在动态分布式缓存系统中,哈希算法的设计是关键点。
使用分布更合理的算法可以使得多个服务节点间的负载相对均衡,可以很大程度上避免资源的浪费以及部分服务器过载。
使用带虚拟节点的一致性哈希算法,可以有效地降低服务硬件环境变化带来的数据迁移代价和风险,从而使分布式缓存系统更加高效稳定。




