算法效率评估
算法algorithm是在有限时间内解决特定问题的一组指令或操作步骤
数据结构 data structure是计算机中组织和存储数据的方式
数据结构与算法高度相关、紧密结合,具体表现以下三个方面:
-
数据结构是算法的基石
数据结构为算法提供了结构化存储的数据,以及用于操作数据的方法 -
算法是数据结构发挥作用的舞台
数据结构本身仅存储数据信息,结合算法才能解决特定问题 -
算法通常可以基于不同的数据结构进行实现
但执行效率可能相差很大,选择合适的数据结构是关键
在算法设计中,先后追求以下两个层面的目标
- 找到问题解法:算法需要在规定的输入范围内,可靠地求得问题的正确解
- 寻求最优解法:同一个问题可能存在多种解法,找到尽可能高效的算法
也就是说,在能够解决问题的前提下,算法效率已成为衡量算法优劣的主要评价指标,它包括以下两个维度
- 时间效率:算法运行速度的快慢
- 空间效率:算法占用内存空间的大小
渐近复杂度分析(asymptotic complexity analysis),简称「复杂度分析」
复杂度分析体现算法运行所需的时间(空间)资源与输入数据大小之间的关系。它描述了随着输入数据大小的增加,算法执行所需时间和空间的增长趋势
- 时间和空间资源分别对应时间复杂
time complexity和空间复杂度space complexity - 随着输入数据大小的增加意味着复杂度反映了算法运行效率与输入数据体量之间的关系
- 时间和空间的增长趋势表示复杂度分析关注的不是运行时间或占用空间的具体值,而是时间或空间增长的快慢
如果函数在返回前的最后一步才进行递归调用,则该函数可以被编译器或解释器优化,使其在空间效率上与迭代相当。这种情况被称为尾递归tail recursion
/* 尾递归 */
int TailRecur(int n, int res) {
// 终止条件
if (n == 0)
return res;
// 尾递归调用
return TailRecur(n - 1, res + n);
}
但许多编译器或解释器不支持尾递归优化
当处理与分治相关的算法问题时,递归往往比迭代的思路更加直观、代码更加易读。以“斐波那契数列”为例:
/* 斐波那契数列:递归 */
int Fib(int n) {
// 终止条件 f(1) = 0, f(2) = 1
if (n == 1 || n == 2)
return n - 1;
// 递归调用 f(n) = f(n-1) + f(n-2)
int res = Fib(n - 1) + Fib(n - 2);
// 返回结果 f(n)
return res;
}
| 迭代 | 递归 | |
|---|---|---|
| 实现方式 | 循环结构 | 函数调用自身 |
| 时间效率 | 效率通常较高。无函数调用开销 | 每次函数调用都会产生开销 |
| 内存使用 | 通常使用固定大小的内存空间 | 累积函数调用可能使用大量的栈帧空间 |
| 适用问题 | 适用于简单循环任务,代码直观、可读性好 | 可适用于子问题分解。如树、图、分治、回溯等,代码结构读性好、简洁、清晰 |
时间复杂度
***时间复杂度指算法运行时间随着数据量变大时的增长趋势
title:计算时间复杂度
操作数量𝑇(𝑛)中的各种系数、常数项都可以被忽略
1. 忽略常数项
2. 省略所有系数
3. 循环嵌套时使用乘法
**时间复杂度由 T(n) 中最高阶的项来决定**
void algorithm(int n) {
int a = 1; // +0(技巧 1)
a = a + n; // +0(技巧 1)
// +n(技巧 2)
for (int i = 0; i < 5 * n + 1; i++) {
cout << 0 << endl;
}
// +n*n(技巧 3)
for (int i = 0; i < 2 * n; i++) {
for (int j = 0; j < n + 1; j++) {
cout << 0 << endl;
}
}
}//因此算法时间复杂度为n的2次方+n
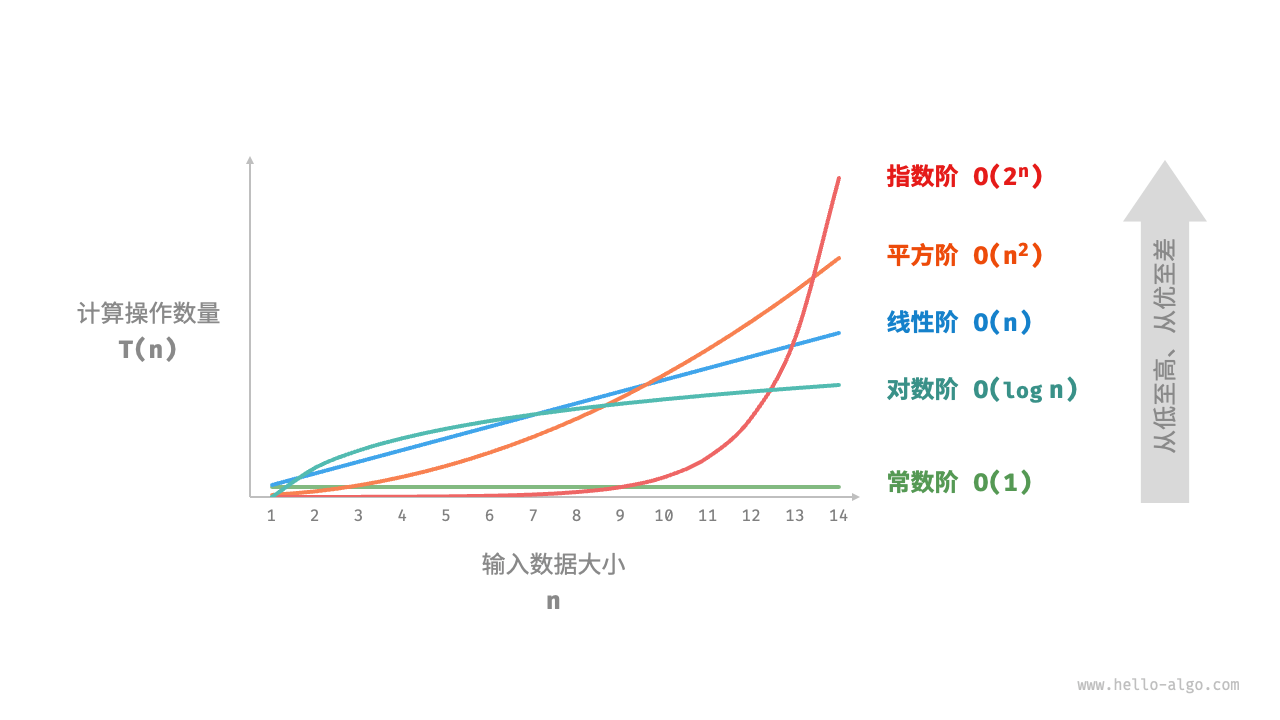
常数阶
/* 常数阶
常数阶的操作数量与输入数据大小 n 无关,即不随着 n 的变化而变化*/
int Constant(int n) {
int count = 0;
int size = 100000;
for (int i = 0; i < size; i++)
count++;
return count;
}
线性阶
/* 线性阶
线性阶的操作数量相对于输入数据大小 n 以线性级别增长。线性阶通常出现在单层循环中*/
int Linear(int n) {
int count = 0;
for (int i = 0; i < n; i++)
count++;
return count;
}
/* 线性阶(遍历数组)
遍历数组和遍历链表等操作的时间复杂度均为 O(n) ,其中 n 为数组或链表的长度*/
int ArrayTraversal(int[] nums) {
int count = 0;
// 循环次数与数组长度成正比
foreach (int num in nums) {
count++;
}
return count;
}
平方阶
/* 平方阶 */
int Quadratic(int n) {
int count = 0;
// 循环次数与数据大小 n 成平方关系
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
count++;
}
}
return count;
}
/* 平方阶(冒泡排序) */
int BubbleSort(int[] nums) {
int count = 0; // 计数器
// 外循环:未排序区间为 [0, i]
for (int i = nums.Length - 1; i > 0; i--) {
// 内循环:将未排序区间 [0, i] 中的最大元素交换至该区间的最右端
for (int j = 0; j < i; j++) {
if (nums[j] > nums[j + 1]) {
// 交换 nums[j] 与 nums[j + 1]
(nums[j + 1], nums[j]) = (nums[j], nums[j + 1]);
count += 3; // 元素交换包含 3 个单元操作
}
}
}
return count;
}
指数阶
/* 指数阶(循环实现) */
int Exponential(int n) {
int count = 0, bas = 1;
// 细胞每轮一分为二,形成数列 1, 2, 4, 8, ..., 2^(n-1)
for (int i = 0; i < n; i++) {
for (int j = 0; j < bas; j++) {
count++;
}
bas *= 2;
}
// count = 1 + 2 + 4 + 8 + .. + 2^(n-1) = 2^n - 1
return count;
}//时间复杂度为 O(2n) 输入 n 表示分裂轮数,返回值 count 表示总分裂次数
/* 指数阶(递归实现) */
int ExpRecur(int n) {
if (n == 1) return 1;
return ExpRecur(n - 1) + ExpRecur(n - 1) + 1;
}
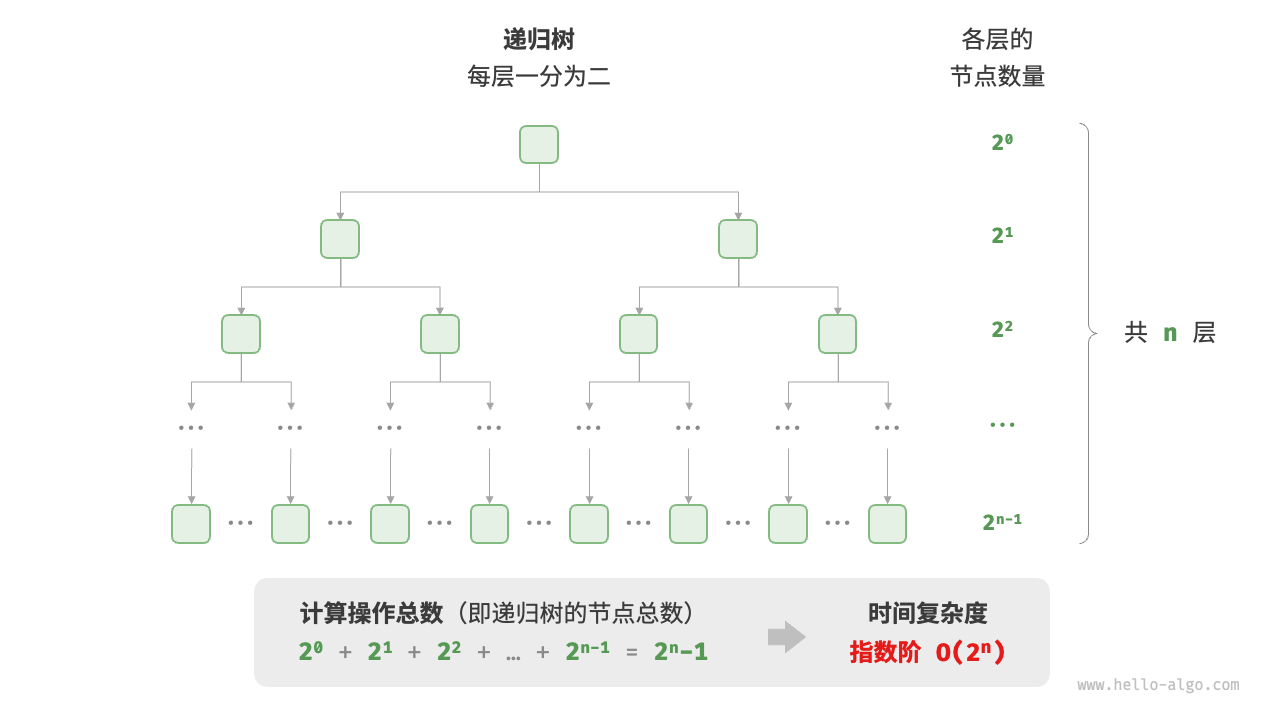
对数阶
/* 对数阶(循环实现)
与指数阶相反,对数阶反映了“每轮缩减到一半”的情况。设输入数据大小为 n ,由于每轮缩减到一半,因此循环次数是 log2n ,即 2n 的反函数*/
int logarithmic(float n) {
int count = 0;
while (n > 1) {
n = n / 2;
count++;
}
return count;
}
/* 对数阶(递归实现) */
int logRecur(float n) {
if (n <= 1)
return 0;
return logRecur(n / 2) + 1;
}
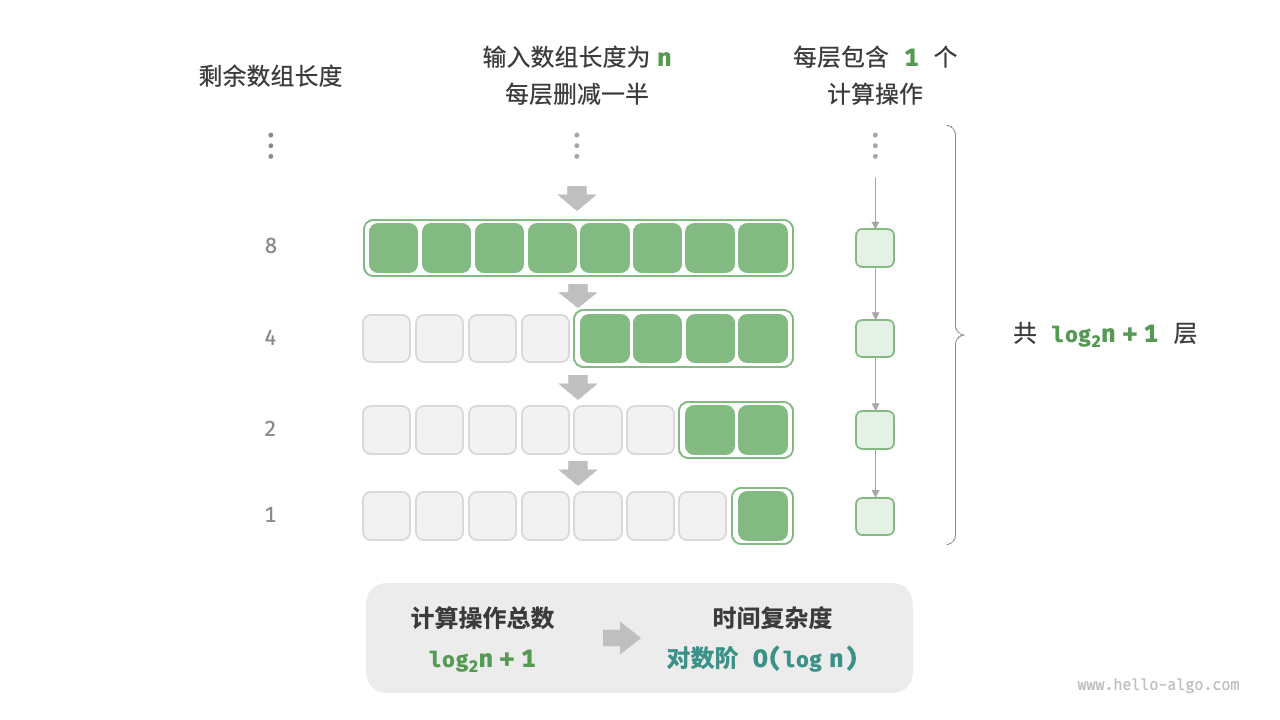
线性对数阶
/* 线性对数阶
线性对数阶常出现于嵌套循环中,两层循环的时间复杂度分别为 O(logn) 和 O(n)*/
int LinearLogRecur(int n) {
if (n <= 1) return 1;
int count = LinearLogRecur(n / 2) + LinearLogRecur(n / 2);
for (int i = 0; i < n; i++) {
count++;
}
return count;
}
//主流排序算法的时间复杂度通常为线性对数阶,例如快速排序、归并排序、堆排序等
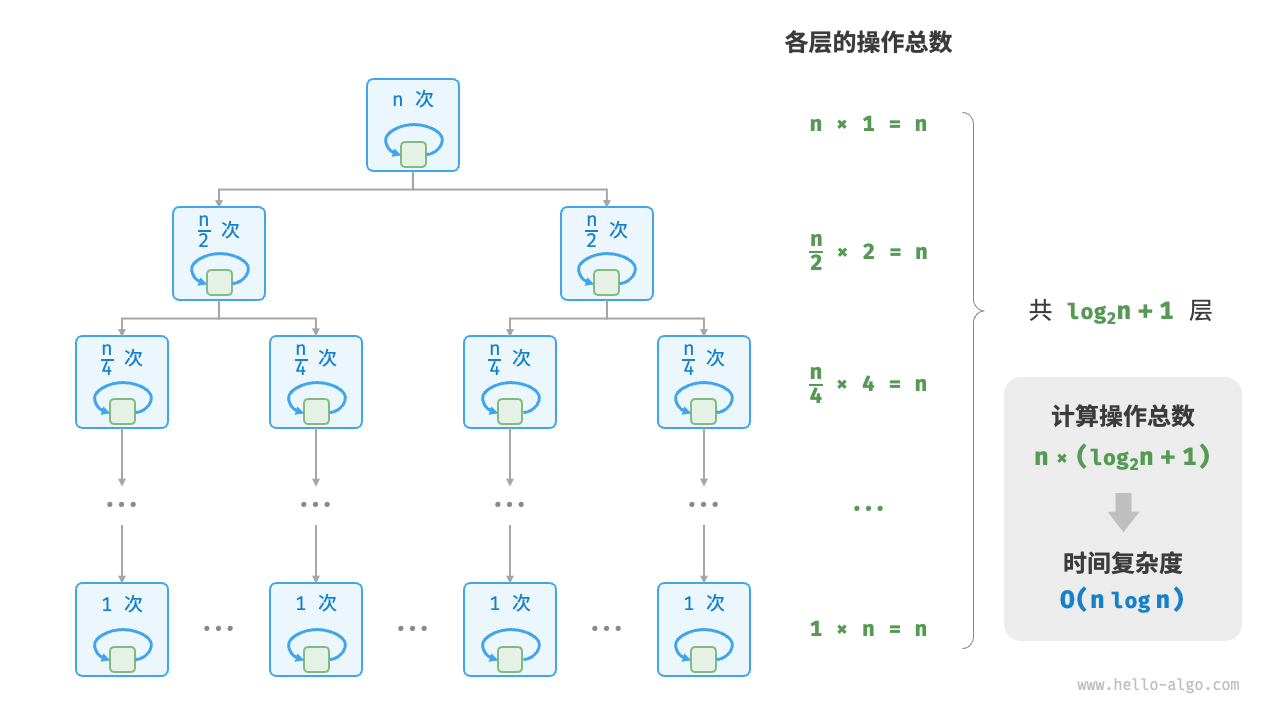
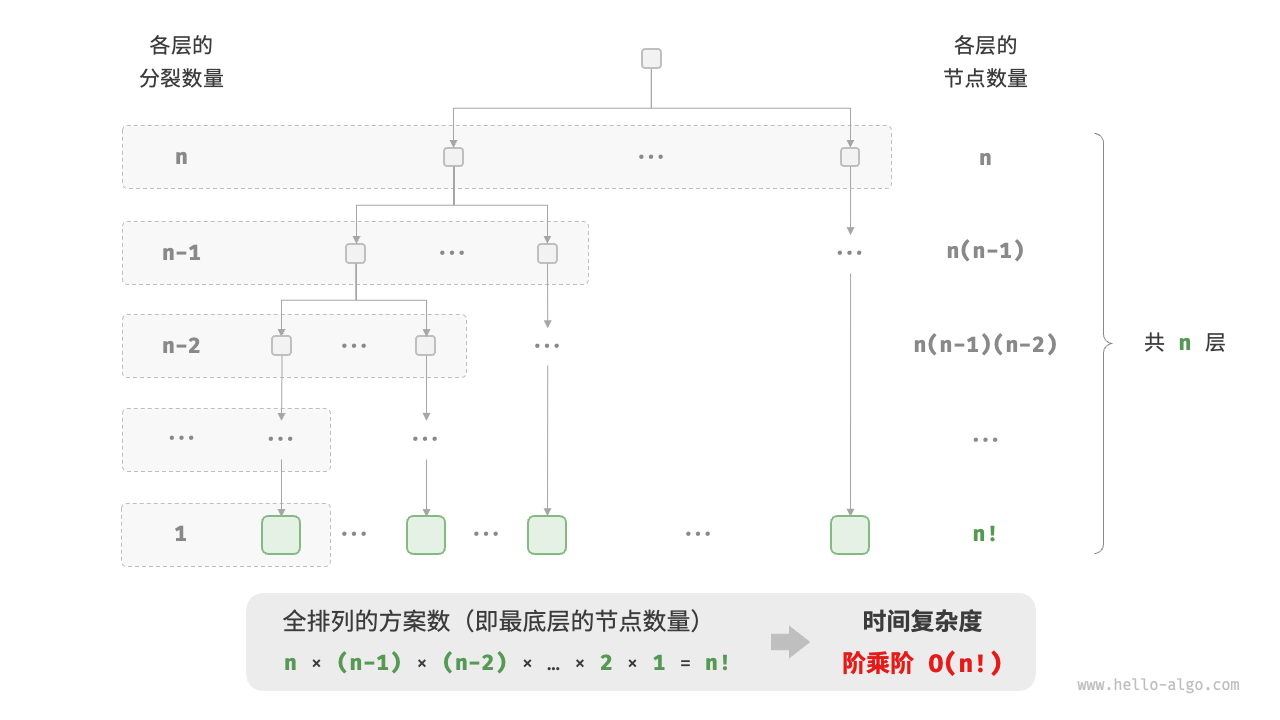
阶乘阶
/* 阶乘阶(迭代实现) */
int FactorialIterative(int n) {
if (n == 0) return 1;
int result = 1;
for (int i = 1; i <= n; i++)
{
result *= i;
}
return result;
}
/* 阶乘阶(递归实现) */
int FactorialRecur(int n) {
if (n == 0) return 1;
return n * FactorialRecursive(n - 1);
}
空间复杂度
***空间复杂度指占用内存空间随着数据量变大时的增长趋势
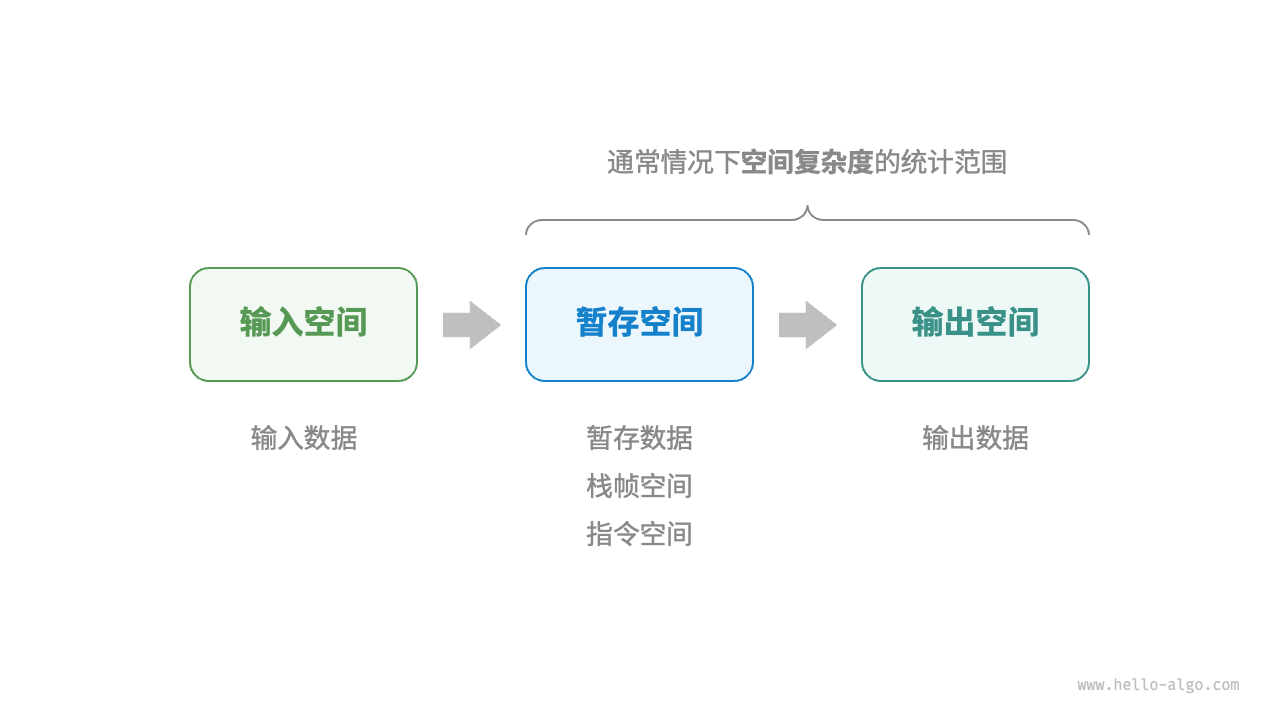
算法在运行过程中使用的内存空间主要包括以下几种
- 输入空间:用于存储算法的输入数据。
- 暂存空间:用于存储算法在运行过程中的变量、对象、函数上下文等数据。
- 输出空间:用于存储算法的输出数据。
一般情况下,空间复杂度的统计范围是“暂存空间”加上“输出空间”。
暂存空间可以进一步划分为三个部分。
- 暂存数据:用于保存算法运行过程中的各种常量、变量、对象等。
- 栈帧空间:用于保存调用函数的上下文数据。系统在每次调用函数时都会在栈顶部创建一个栈帧,函数返回后,栈帧空间会被释放。
- 指令空间:用于保存编译后的程序指令,在实际统计中通常忽略不计
在分析一段程序的空间复杂度时,通常统计暂存数据、栈帧空间和输出数据三部分
/* 循环的空间复杂度为 O(1) */
void Loop(int n) {
for (int i = 0; i < n; i++) {
//执行常数操作
}
}
/* 递归的空间复杂度为 O(n) */
int Recur(int n) {
if (n == 1) return 1;
return Recur(n - 1);
}
collapse:closed
函数 `loop()` 和 `recur()` 的时间复杂度都为 O(n) ,但空间复杂度不同。
- 函数 `loop()` 在循环中调用了 n 次 `function()` ,每轮中的 `function()` 都返回并释放了栈帧空间,因此空间复杂度仍为 O(1) 。
- 递归函数 `recur()` 在运行过程中会同时存在 n 个未返回的 `recur()` ,从而占用 O(n) 的栈帧空间。
常数阶
int Function() {
// 执行常数操作
return 0;
}
/* 常数阶
在循环中初始化变量或调用函数而占用的内存,在进入下一循环后就会被释放,因此不会累积占用空间,空间复杂度仍为 O(1)*/
void Constant(int n) {
// 常量、变量、对象占用 O(1) 空间
int a = 0;
int b = 0;
int[] nums = new int[10000];
ListNode node = new(0);
// 循环中的变量占用 O(1) 空间
for (int i = 0; i < n; i++) {
int c = 0;
}
// 循环中的函数占用 O(1) 空间
for (int i = 0; i < n; i++) {
Function();
}
}
线性阶
/* 线性阶
线性阶常见于元素数量与 n 成正比的数组、链表、栈、队列等*/
void Linear(int n) {
// 长度为 n 的数组占用 O(n) 空间
int[] nums = new int[n];
// 长度为 n 的列表占用 O(n) 空间
List<ListNode> nodes = [];
for (int i = 0; i < n; i++) {
nodes.Add(new ListNode(i));
}
// 长度为 n 的哈希表占用 O(n) 空间
Dictionary<int, string> map = [];
for (int i = 0; i < n; i++) {
map.Add(i, i.ToString());
}
}
平方阶
/* 平方阶
平方阶常见于矩阵和图,元素数量与 n 成平方关系*/
void quadratic(int n) {
// 矩阵占用 O(n^2) 空间
int[][] numMatrix = new int[n][n];
// 二维列表占用 O(n^2) 空间
List<List<Integer>> numList = new ArrayList<>();
for (int i = 0; i < n; i++) {
List<Integer> tmp = new ArrayList<>();
for (int j = 0; j < n; j++) {
tmp.add(0);
}
numList.add(tmp);
}
}
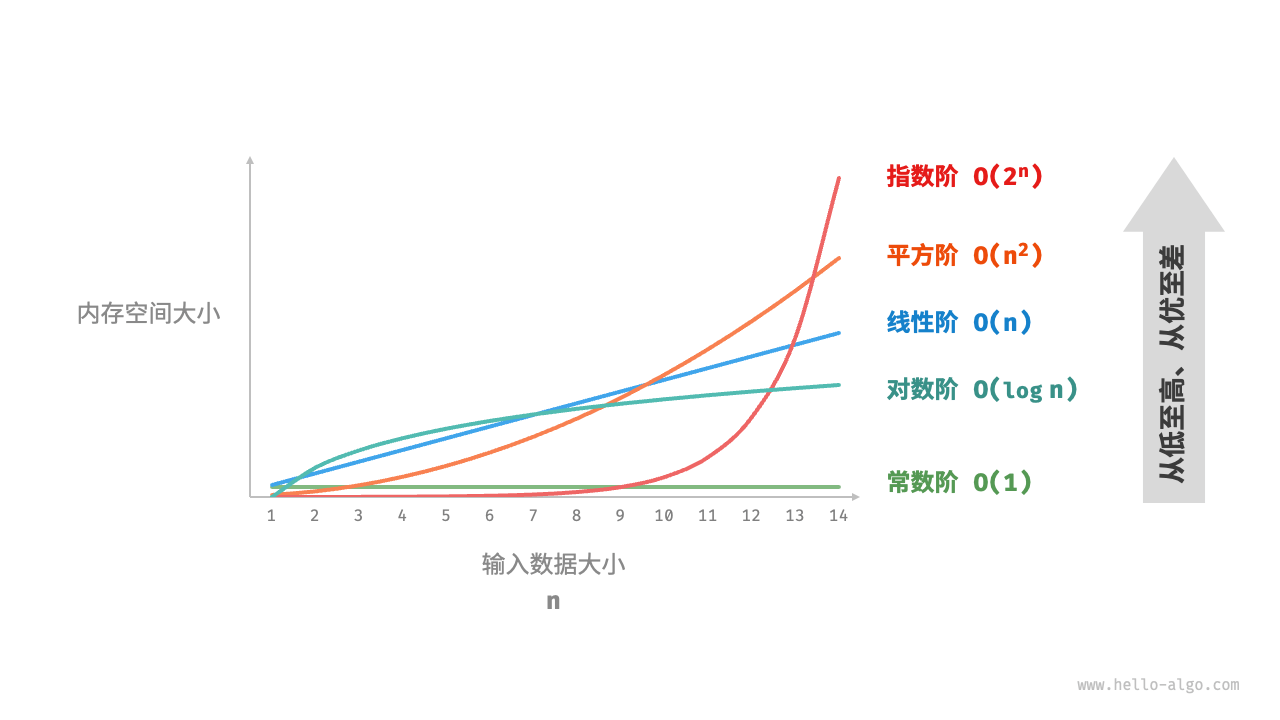
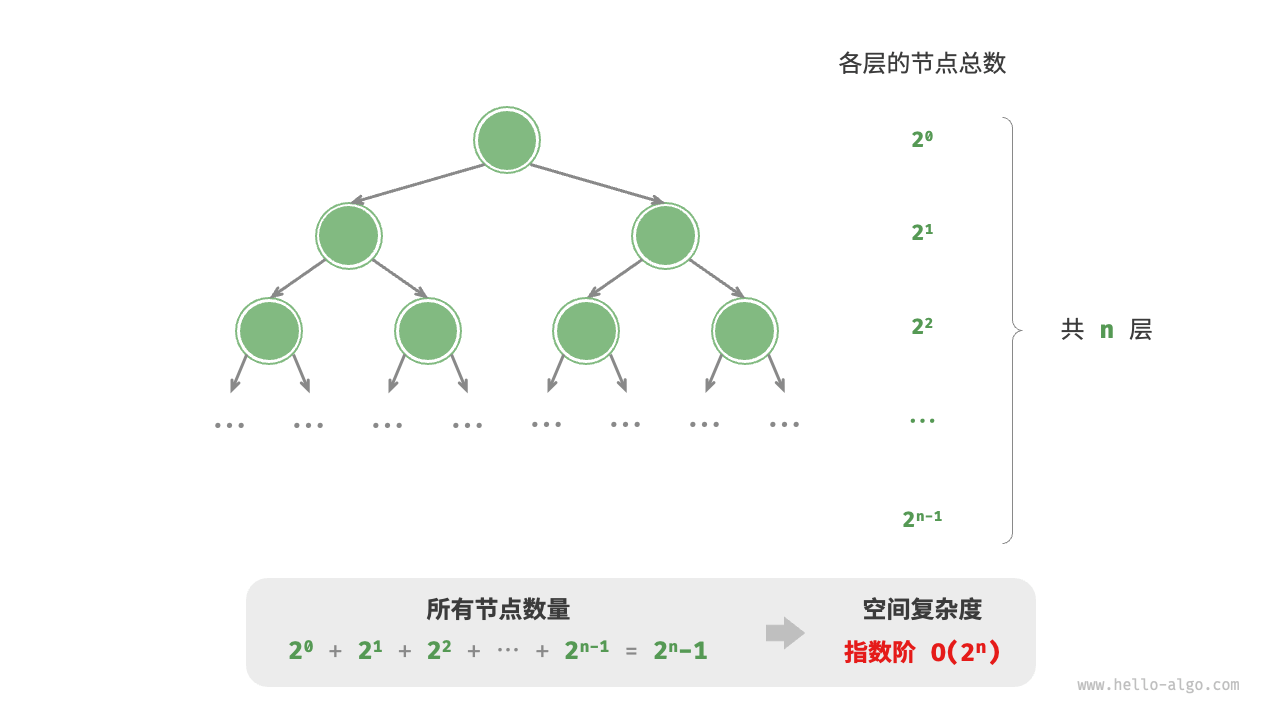
指数阶
/* 指数阶(建立满二叉树)
指数阶常见于二叉树。层数为 n 的“满二叉树”的节点数量为 2n−1 ,占用 O(2n) 空间*/
TreeNode? BuildTree(int n) {
if (n == 0) return null;
TreeNode root = new(0) {
left = BuildTree(n - 1),
right = BuildTree(n - 1)
};
return root;
}
对数阶
对数阶常见于分治算法。例如归并排序,输入长度为 n 的数组,每轮递归将数组从中点处划分为两半,形成高度为 logn 的递归树,使用 O(logn) 栈帧空间。
再例如将数字转化为字符串,输入一个正整数 n ,它的位数为 $⌊\log_{10}n⌋+1$ ,即对应字符串长度为 $⌊\log_{10}n⌋+1$ ,因此空间复杂度为$O(\log_{10}n+1)=O(\logn)$
数据结构分类
- **逻辑结构:线性与非线性
非线性数据结构可以进一步划分为树形结构和网状结构:
- *树形结构:树、堆、哈希表,元素之间是一对多的关系
- *网状结构:图,元素之间是多对多的关系
![]()
- **物理结构:连续与分散
![]()
数字都是以补码的形式存储在计算机中
Hello算法-数字编码
计算机内部的硬件电路主要是基于加法运算设计的,通过将加法与一些基本逻辑运算结合,计算机能够实现各种其他的数学运算
-
UTF‑8是国际上使用最广泛的 Unicode 编码方法。它是一种可变长的编码,使用1到4个字节来表示一个字符,根据字符的复杂性而变。ASCII 字符只需要 1 个字节,拉丁字母和希腊字母需要 2 个字节,常用的中文字符需要 3 个字节,其他的一些生僻字符需要 4 个字节。
-
UTF‑8 的编码规则并不复杂,分为以下两种情况:
-
对于长度为 1 字节的字符,将最高位设置为0、其余 7 位设置为 Unicode 码点。值得注意的是,ASCII字符在 Unicode 字符集中占据了前 128 个码点。也就是说,UTF‑8 编码可以向下兼容 ASCII 码。这意味着我们可以使用 UTF‑8 来解析年代久远的 ASCII 码文本
-
对于长度为𝑛字节的字符(其中𝑛 > 1),将首个字节的高𝑛位都设置为1、第𝑛 + 1位设置为0;从第二个字节开始,将每个字节的高 2 位都设置为10;其余所有位用于填充字符的 Unicode 码点
-
UTF‑16 和 UTF‑32 是等长的编码方法。在编码中文时,UTF‑16比 UTF‑8 的占用空间更小。Java 和 C# 等编程语言默认使用 UTF‑16 编码
数组与链表
数组
*数组定义与存储方式
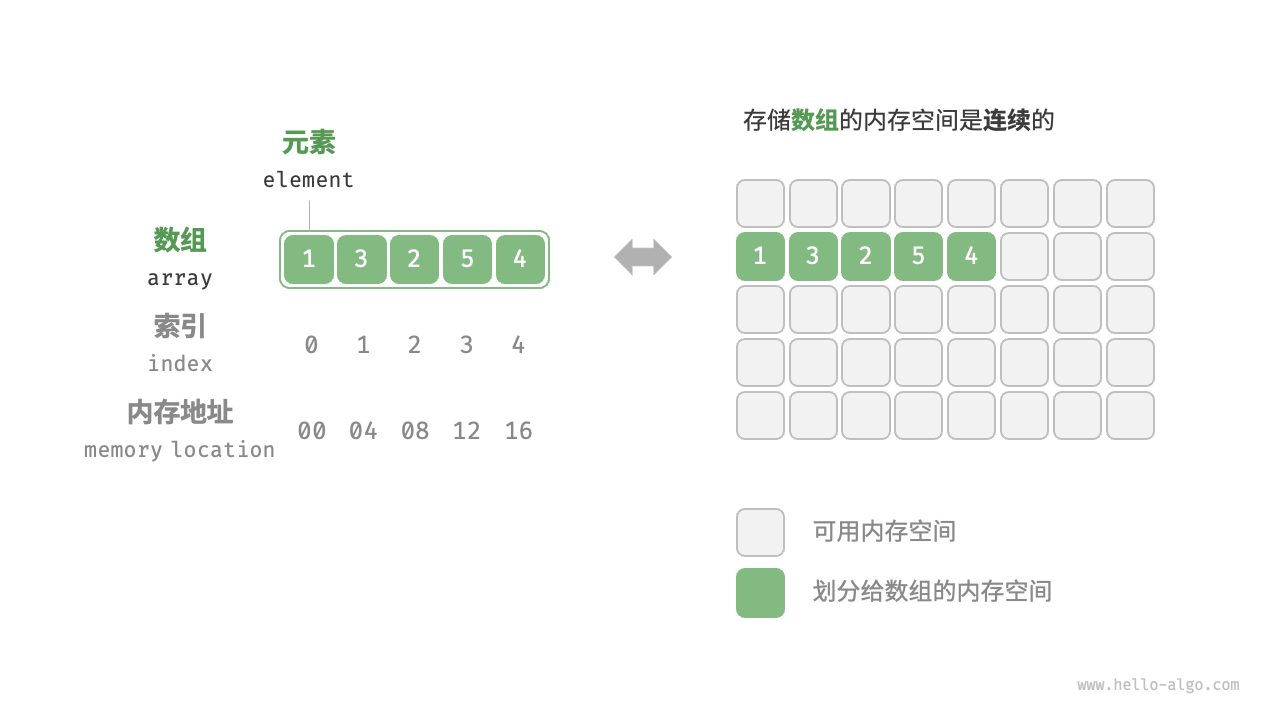
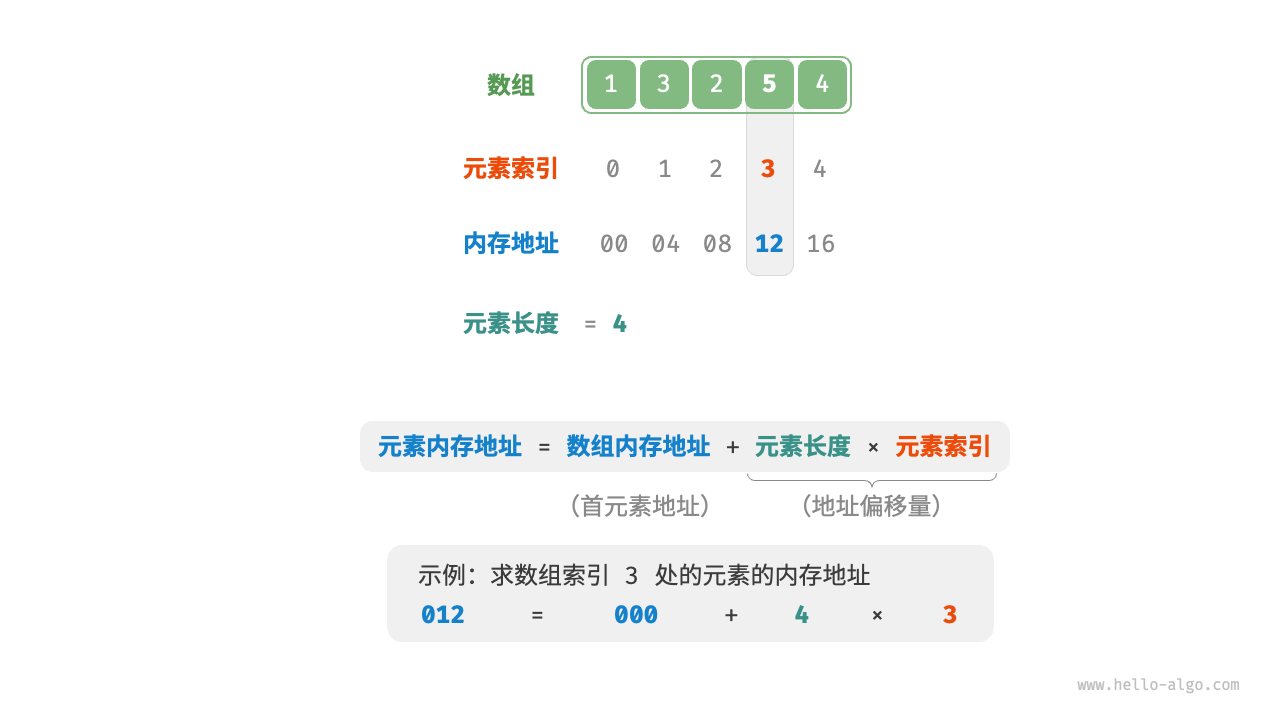
*数组元素的内存地址计算
**索引本质上是内存地址的偏移量
/* 随机访问元素
数组中访问元素非常高效,可以在 O(1) 时间内随机访问数组中的任意一个元素*/
int RandomAccess(int[] nums) {
Random random = new();
// 在区间 [0, nums.Length) 中随机抽取一个数字
int randomIndex = random.Next(nums.Length);
// 获取并返回随机元素
int randomNum = nums[randomIndex];
return randomNum;
}
*数组插入元素
如果想在数组中间插入一个元素,则需要将该元素之后的所有元素都向后移动一位,之后再把元素赋值给该索引
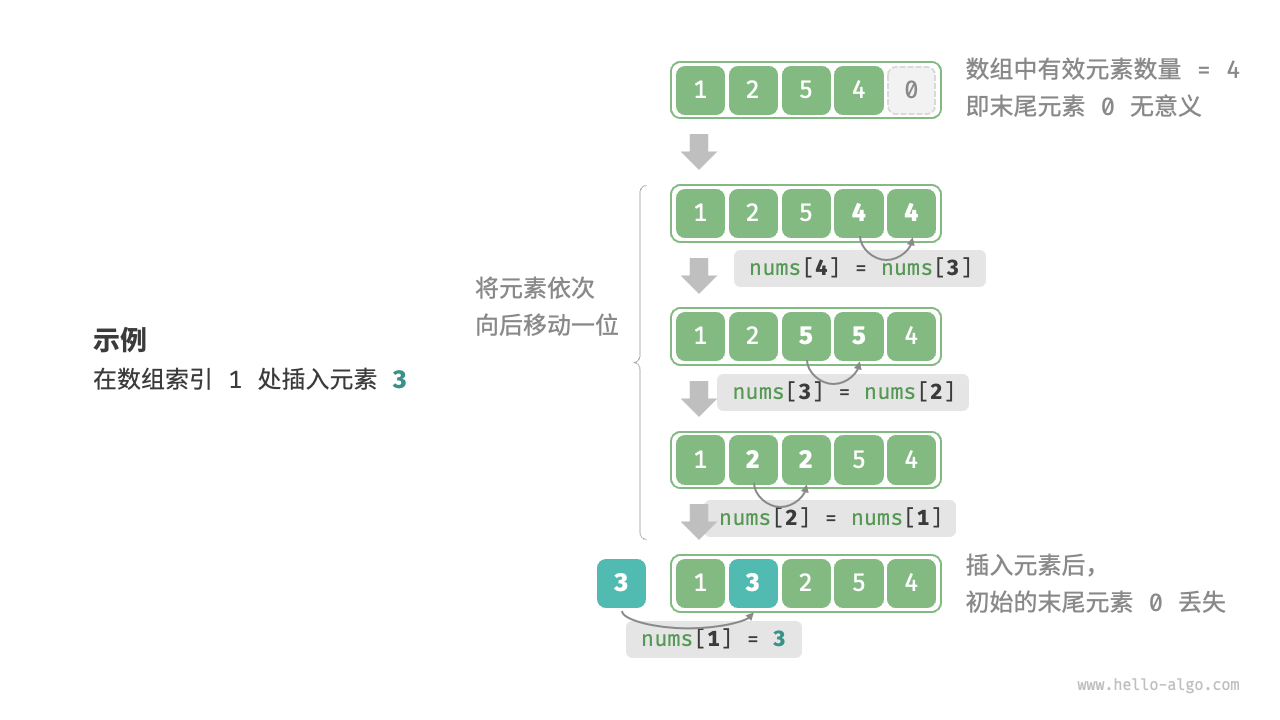
/* 在数组的索引 index 处插入元素 num */
void Insert(int[] nums, int num, int index) {
// 把索引 index 以及之后的所有元素向后移动一位
for (int i = nums.Length - 1; i > index; i--) {
nums[i] = nums[i - 1];
}
// 将 num 赋给 index 处的元素
nums[index] = num;
}
*删除元素
若想删除索引 i 处的元素,则需要把索引 i 之后的元素都向前移动一位
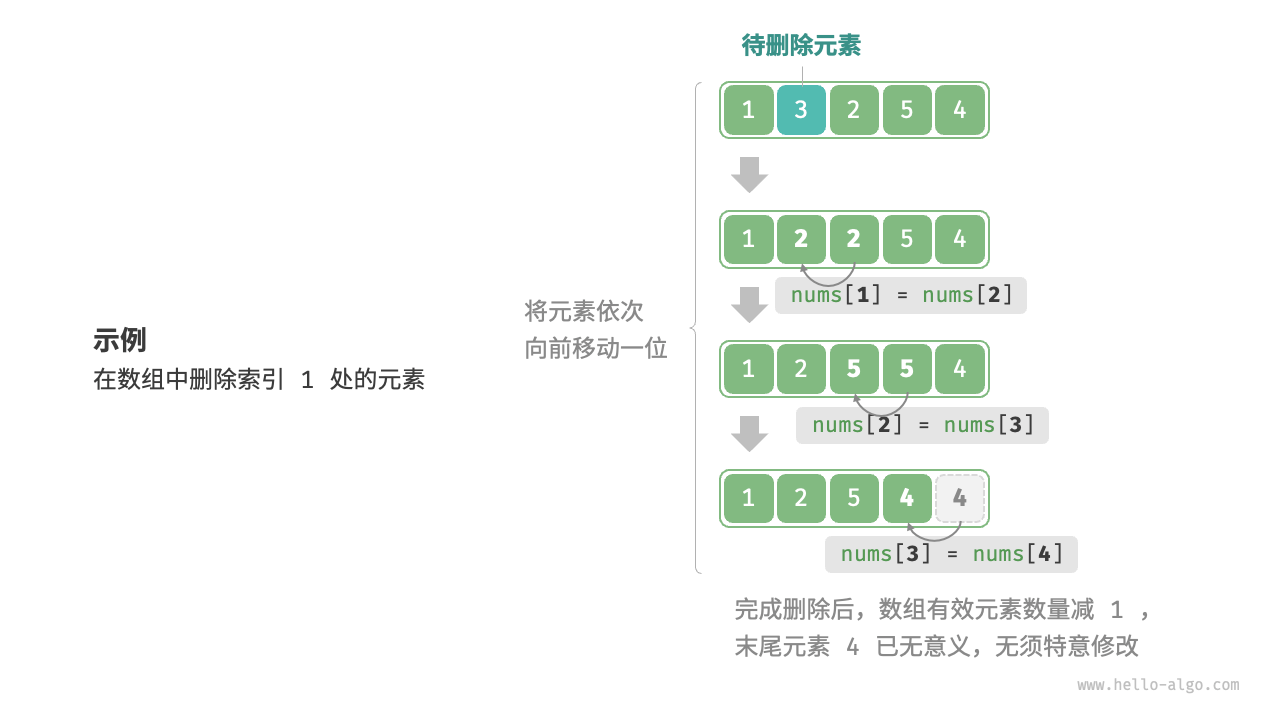
/* 删除索引 index 处的元素 */
void Remove(int[] nums, int index) {
// 把索引 index 之后的所有元素向前移动一位
for (int i = index; i < nums.Length - 1; i++) {
nums[i] = nums[i + 1];
}
}
*遍历数组
/* 遍历数组 */
void Traverse(int[] nums) {
int count = 0;
// 通过索引遍历数组
for (int i = 0; i < nums.Length; i++) {
count += nums[i];
}
// 直接遍历数组元素
foreach (int num in nums) {
count += num;
}
}
*查找元素
/* 在数组中查找指定元素
在数组中查找指定元素需要遍历数组,每轮判断元素值是否匹配,若匹配则输出对应索引*/
int Find(int[] nums, int target) {
for (int i = 0; i < nums.Length; i++) {
if (nums[i] == target)
return i;
}
return -1;
}
*扩容数组
/* 扩展数组长度 */
int[] Extend(int[] nums, int enlarge) {
// 初始化一个扩展长度后的数组
int[] res = new int[nums.Length + enlarge];
// 将原数组中的所有元素复制到新数组
for (int i = 0; i < nums.Length; i++) {
res[i] = nums[i];
}
// 返回扩展后的新数组
return res;
}
***数组典型应用
数组是一种基础且常见的数据结构,既频繁应用在各类算法之中,也可用于实现各种复杂数据结构。
- 随机访问:如果我们想随机抽取一些样本,那么可以用数组存储,并生成一个随机序列,根据索引实现随机抽样。
- 排序和搜索:数组是排序和搜索算法最常用的数据结构。快速排序、归并排序、二分查找等都主要在数组上进行。
- 查找表:当需要快速查找一个元素或其对应关系时,可以使用数组作为查找表。假如我们想实现字符到 ASCII 码的映射,则可以将字符的 ASCII 码值作为索引,对应的元素存放在数组中的对应位置。
- 机器学习:神经网络中大量使用了向量、矩阵、张量之间的线性代数运算,这些数据都是以数组的形式构建的。数组是神经网络编程中最常使用的数据结构。
- 数据结构实现:数组可以用于实现栈、队列、哈希表、堆、图等数据结构。例如,图的邻接矩阵表示实际上是一个二维数组。
链表
*链表定义与存储方式
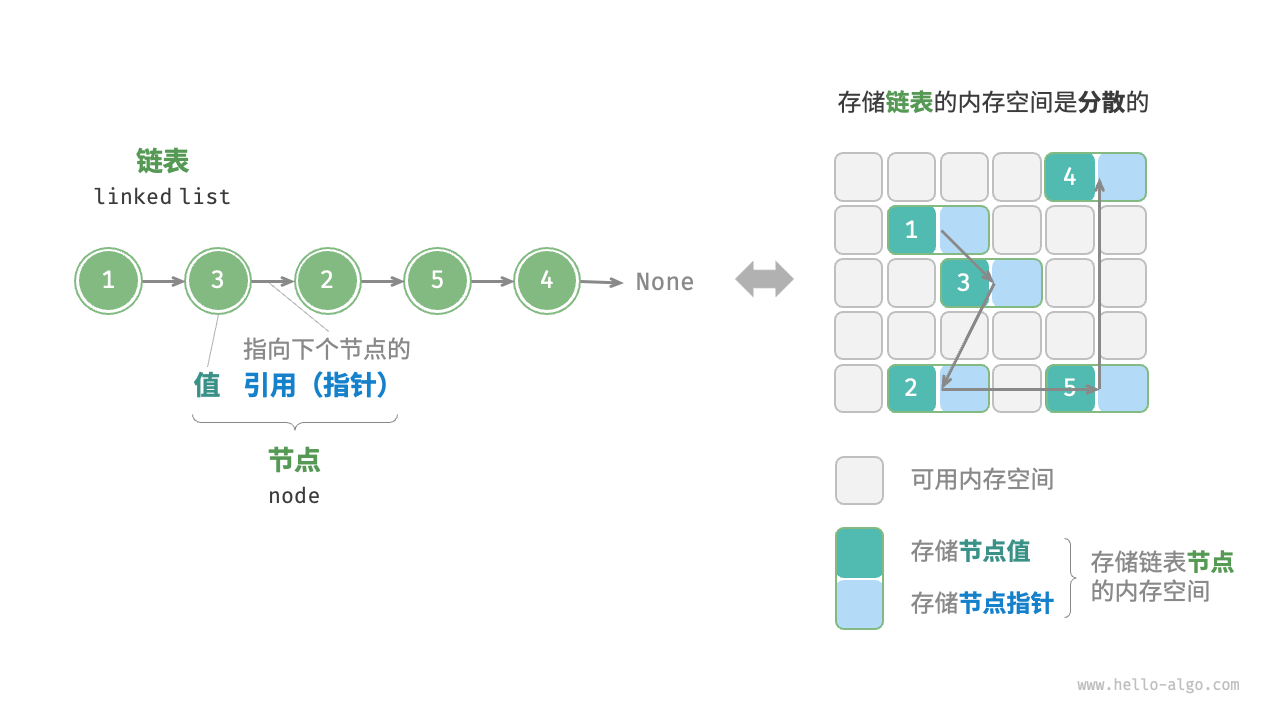
链表的组成单位是节点(node)对象。每个节点都包含两项数据:节点的“值”和指向下一节点的“引用”。
- 链表的首个节点被称为“头节点”,最后一个节点被称为“尾节点”。
- 尾节点指向的是“空”,它在 Java、C++ 和 Python 中分别被记为
null、nullptr和None。 - 在 C、C++、Go 和 Rust 等支持指针的语言中,上述“引用”应被替换为“指针”
/* 链表节点类 */
class ListNode(int x) { //构造函数
int val = x; // 节点值
ListNode? next; // 指向下一节点的引用
}
*初始化链表
建立链表分为两步,第一步是初始化各个节点对象,第二步是构建节点之间的引用关系。初始化完成后,我们就可以从链表的头节点出发,通过引用指向 next 依次访问所有节点
/* 初始化链表 1 -> 3 -> 2 -> 5 -> 4 */
// 初始化各个节点
ListNode n0 = new(1);
ListNode n1 = new(3);
ListNode n2 = new(2);
ListNode n3 = new(5);
ListNode n4 = new(4);
// 构建节点之间的引用
n0.next = n1;
n1.next = n2;
n2.next = n3;
n3.next = n4;
*插入节点
在相邻的两个节点 n0 和 n1 之间插入一个新节点 P ,则只需改变两个节点引用(指针)即可,时间复杂度为 O(1)
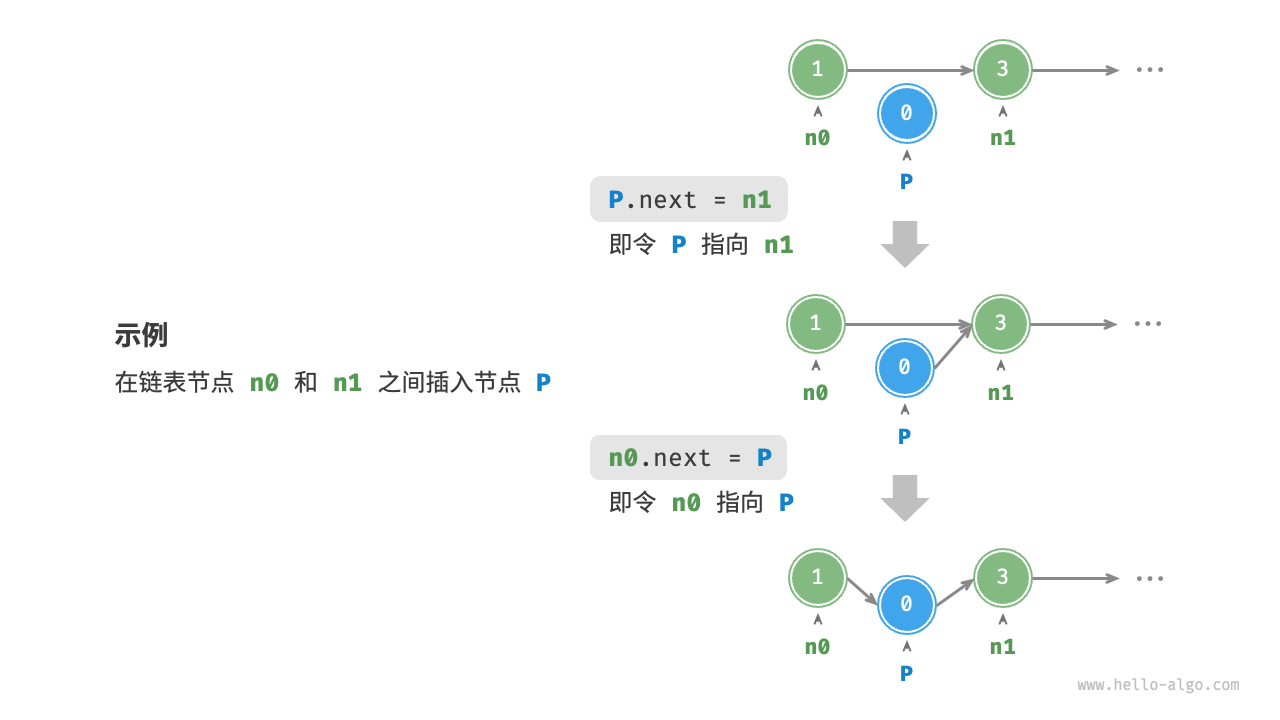
/* 在链表的节点 n0 之后插入节点 P */
void Insert(ListNode n0, ListNode P) {
ListNode? n1 = n0.next;
P.next = n1;
n0.next = P;
}
*删除节点
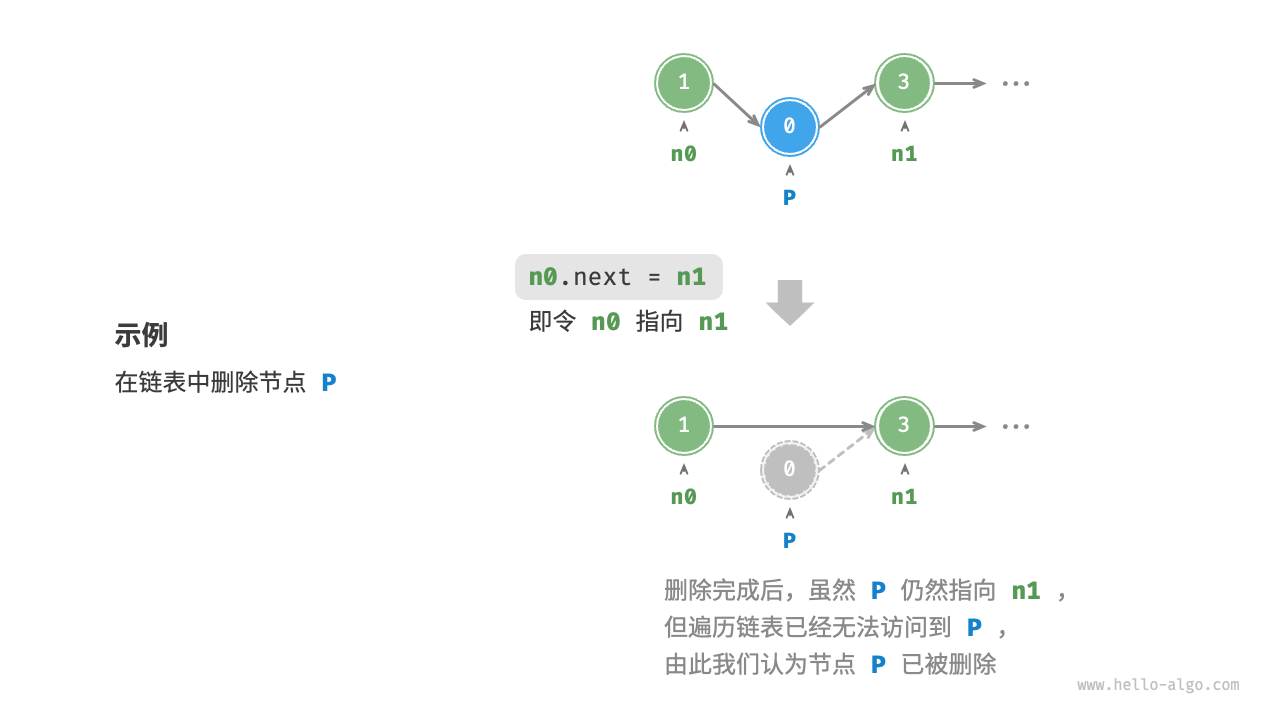
/* 删除链表的节点 n0 之后的首个节点 */
void Remove(ListNode n0) {
if (n0.next == null)
return;
// n0 -> P -> n1
ListNode P = n0.next;
ListNode? n1 = P.next;
n0.next = n1;
}
*访问节点
需要从头节点出发,逐个向后遍历,直至找到目标节点。也就是说,访问链表的第 i 个节点需要循环 i−1 轮,时间复杂度为 O(n)
/* 访问链表中索引为 index 的节点 */
ListNode? Access(ListNode? head, int index) {
for (int i = 0; i < index; i++) {
if (head == null)
return null;
head = head.next;
}
return head;
}
*查找节点
遍历链表,查找其中值为 target 的节点,输出该节点在链表中的索引。此过程也属于线性查找
/* 在链表中查找值为 target 的首个节点 */
int Find(ListNode? head, int target) {
int index = 0;
while (head != null) {
if (head.val == target)
return index;
head = head.next;
index++;
}
return -1;
}
*数组与链表的效率对比
| 数组 | 链表 | |
|---|---|---|
| 存储方式 | 连续内存空间 | 分散内存空间 |
| 容量扩展 | 长度不可变 | 可灵活扩展 |
| 内存效率 | 元素占用内存少、但可能浪费空间 | 元素占用内存多 |
| 访问元素 | ||
| 添加元素 | ||
| 删除元素 |
*常见的链表类型
- 单向链表:即前面介绍的普通链表。单向链表的节点包含值和指向下一节点的引用两项数据。我们将首个节点称为头节点,将最后一个节点称为尾节点,尾节点指向空
None - 环形链表:如果令单向链表的尾节点指向头节点(首尾相接),则得到一个环形链表。在环形链表中,任意节点都可以视作头节点
- 双向链表:与单向链表相比,双向链表记录了两个方向的引用。双向链表的节点定义同时包含指向后继节点(下一个节点)和前驱节点(上一个节点)的引用(指针)。相较于单向链表,双向链表更具灵活性,可以朝两个方向遍历链表,但相应地也需要占用更多的内存空间
![]()
*链表典型应用
单向链表通常用于实现栈、队列、哈希表和图等数据结构:
- 栈与队列:当插入和删除操作都在链表的一端进行时,它表现的特性为先进后出,对应栈;当插入操作在链表的一端进行,删除操作在链表的另一端进行,它表现的特性为先进先出,对应队列。
- 哈希表:链式地址是解决哈希冲突的主流方案之一,在该方案中,所有冲突的元素都会被放到一个链表中。
- 图:邻接表是表示图的一种常用方式,其中图的每个顶点都与一个链表相关联,链表中的每个元素都代表与该顶点相连的其他顶点。
*双向链表常用于需要快速查找前一个和后一个元素的场景:
- 高级数据结构:比如在红黑树、B 树中,我们需要访问节点的父节点,这可以通过在节点中保存一个指向父节点的引用来实现,类似于双向链表。
- 浏览器历史:在网页浏览器中,当用户点击前进或后退按钮时,浏览器需要知道用户访问过的前一个和后一个网页。双向链表的特性使得这种操作变得简单。
- LRU 算法:在缓存淘汰(LRU)算法中,我们需要快速找到最近最少使用的数据,以及支持快速添加和删除节点。这时候使用双向链表就非常合适。
*环形链表常用于需要周期性操作的场景,比如操作系统的资源调度:
- 时间片轮转调度算法:在操作系统中,时间片轮转调度算法是一种常见的 CPU 调度算法,它需要对一组进程进行循环。每个进程被赋予一个时间片,当时间片用完时,CPU 将切换到下一个进程。这种循环操作可以通过环形链表来实现。
- 数据缓冲区:在某些数据缓冲区的实现中,也可能会使用环形链表。比如在音频、视频播放器中,数据流可能会被分成多个缓冲块并放入一个环形链表,以便实现无缝播放
列表
*列表可以基于链表或数组实现,许多编程语言中的标准库提供的列表是基于动态数组实现的
- 链表天然可以看作一个列表,其支持元素增删查改操作,并且可以灵活动态扩容
- 数组也支持元素增删查改,但由于其长度不可变,因此只能看作一个具有长度限制的列表
*初始化列表
/* 初始化列表 */
// 无初始值
List<int> nums1 = [];
// 有初始值
int[] numbers = [1, 3, 2, 5, 4];
List<int> nums = [.. numbers];//使用扩展操作符 .. 来将数组 numbers 中的所有元素展开并初始化一个新的整数列表
*访问元素
列表本质上是数组,因此可以在 O(1) 时间内访问和更新元素
/* 访问元素 */
int num = nums[1]; // 访问索引 1 处的元素
/* 更新元素 */
nums[1] = 0; // 将索引 1 处的元素更新为 0
*插入与删除元素
列表可以自由地添加与删除元素。在列表尾部添加元素的时间复杂度为 O(1) ,但插入和删除元素的效率仍与数组相同,时间复杂度为 O(n)
/* 清空列表 */
nums.Clear();
/* 在尾部添加元素 */
nums.Add(1);
nums.Add(3);
nums.Add(2);
nums.Add(5);
nums.Add(4);
/* 在中间插入元素 */
nums.Insert(3, 6); //在索引3处插入数字6
/* 删除元素 */
nums.RemoveAt(3); //删除索引3处的元素
*遍历列表
与数组一样,列表可以根据索引遍历,也可以直接遍历各元素
/* 通过索引遍历列表 */
int count = 0;
for (int i = 0; i < nums.Count; i++) {
count += nums[i];
}
/* 直接遍历列表元素 */
count = 0;
foreach (int num in nums) {
count += num;
}
*拼接列表
/* 拼接两个列表 */
List<int> nums1 = [6, 8, 7, 10, 9];
nums.AddRange(nums1); // 将列表 nums1 拼接到 nums 之后
*排序列表
/* 排序列表 */
nums.Sort(); // 排序后,列表元素从小到大排列
*尝试实现一个简易版列表,包括以下三个重点设计:
- 初始容量:选取一个合理的数组初始容量。在本示例中,我们选择 10 作为初始容量。
- 数量记录:声明一个变量
size,用于记录列表当前元素数量,并随着元素插入和删除实时更新。根据此变量,我们可以定位列表尾部,以及判断是否需要扩容。 - 扩容机制:若插入元素时列表容量已满,则需要进行扩容。先根据扩容倍数创建一个更大的数组,再将当前数组的所有元素依次移动至新数组。在本示例中,我们规定每次将数组扩容至之前的 2 倍。
/* 列表类 */
class MyList {
private int[] arr; // 数组(存储列表元素)
private int arrCapacity = 10; // 列表容量
private int arrSize = 0; // 列表长度(当前元素数量)
private readonly int extendRatio = 2; // 每次列表扩容的倍数
/* 构造方法 */
public MyList() {
arr = new int[arrCapacity];
}
/* 获取列表长度(当前元素数量)*/
public int Size() {
return arrSize;
}
/* 获取列表容量 */
public int Capacity() {
return arrCapacity;
}
/* 访问元素 */
public int Get(int index) {
// 索引如果越界,则抛出异常,下同
if (index < 0 || index >= arrSize)
throw new IndexOutOfRangeException("索引越界");
return arr[index];
}
/* 更新元素 */
public void Set(int index, int num) {
if (index < 0 || index >= arrSize)
throw new IndexOutOfRangeException("索引越界");
arr[index] = num;
}
/* 在尾部添加元素 */
public void Add(int num) {
// 元素数量超出容量时,触发扩容机制
if (arrSize == arrCapacity)
ExtendCapacity();
arr[arrSize] = num;
// 更新元素数量
arrSize++;
}
/* 在中间插入元素 */
public void Insert(int index, int num) {
if (index < 0 || index >= arrSize)
throw new IndexOutOfRangeException("索引越界");
// 元素数量超出容量时,触发扩容机制
if (arrSize == arrCapacity)
ExtendCapacity();
// 将索引 index 以及之后的元素都向后移动一位
for (int j = arrSize - 1; j >= index; j--) {
arr[j + 1] = arr[j];
}
arr[index] = num;
// 更新元素数量
arrSize++;
}
/* 删除元素 */
public int Remove(int index) {
if (index < 0 || index >= arrSize)
throw new IndexOutOfRangeException("索引越界");
int num = arr[index];
// 将索引 index 之后的元素都向前移动一位
for (int j = index; j < arrSize - 1; j++) {
arr[j] = arr[j + 1];
}
// 更新元素数量
arrSize--;
// 返回被删除的元素
return num;
}
/* 列表扩容 */
public void ExtendCapacity() {
// 新建一个长度为 arrCapacity * extendRatio 的数组,并将原数组复制到新数组
Array.Resize(ref arr, arrCapacity * extendRatio);
// 更新列表容量
arrCapacity = arr.Length;
}
/* 将列表转换为数组 */
public int[] ToArray() {
// 仅转换有效长度范围内的列表元素
int[] arr = new int[arrSize];
for (int i = 0; i < arrSize; i++) {
arr[i] = Get(i);
}
return arr;
}
}
内存与缓存
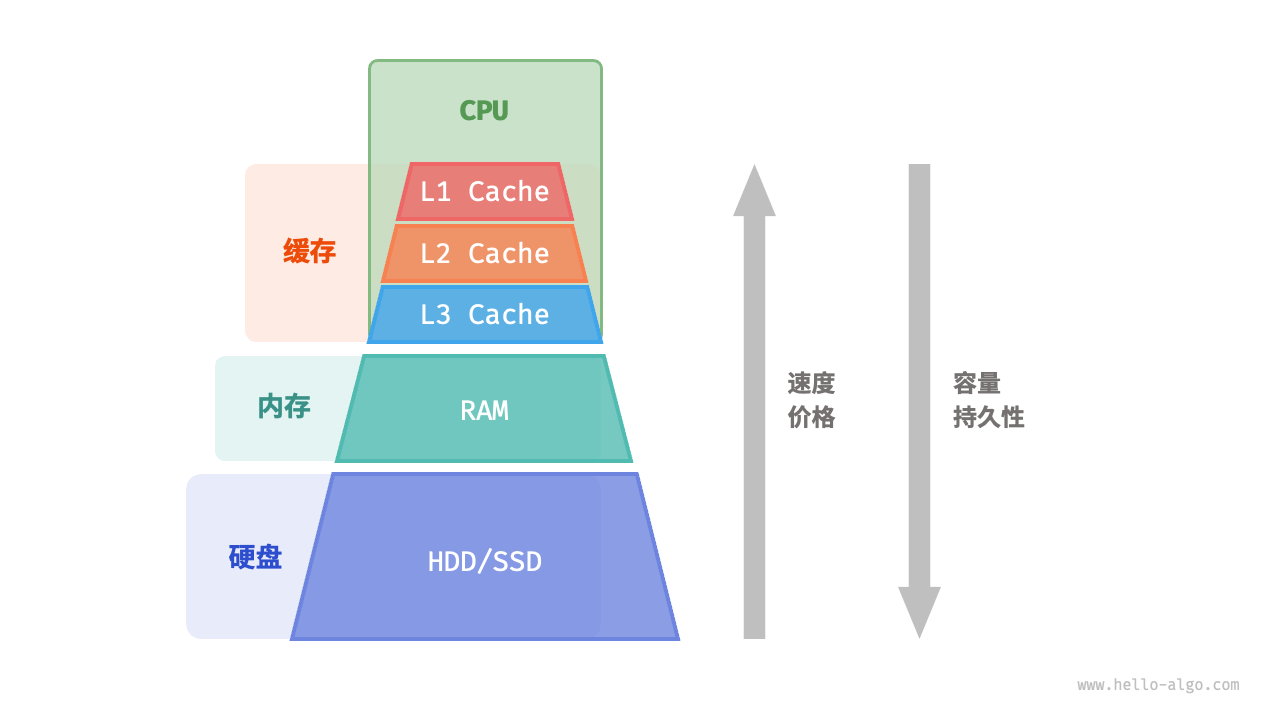
硬盘用于长期存储大量数据,内存用于临时存储程序运行中正在处理的数据,而缓存则用于存储经常访问的数据和指令
程序运行时,数据会从硬盘中被读取到内存中,供 CPU 计算使用。缓存可以看作 CPU 的一部分,它通过智能地从内存加载数据,给 CPU 提供高速的数据读取,从而显著提升程序的执行效率,减少对较慢的内存的依赖
在内存空间利用方面,数组和链表各自具有优势和局限性
-
内存是有限的,且同一块内存不能被多个程序共享
- 数组的元素紧密排列,不需要额外的空间来存储链表节点间的引用(指针),因此空间效率更高。
- 数组需要一次性分配足够的连续内存空间,这可能导致内存浪费
- 数组扩容也需要额外的时间和空间成本
- 链表以“节点”为单位进行动态内存分配和回收,提供了更大的灵活性。
-
在程序运行时,随着反复申请与释放内存,空闲内存的碎片化程度会越来越高,从而导致内存的利用效率降低
- 数组由于其连续的存储方式,相对不容易导致内存碎片化
- 链表的元素是分散存储的,在频繁的插入与删除操作中,更容易导致内存碎片化
数据结构的缓存效率
当 CPU 尝试访问的数据不在缓存中时,就会发生缓存未命中 cache miss,此时CPU不得不从速度较慢的内存中加载所需数据。
“缓存未命中”越少,CPU 读写数据的效率就越高,程序性能也就越好。我们将CPU从缓存中成功获取数据的比例称为缓存命中率 cache hit rate,这个指标通常用来衡量缓存效率
为了尽可能达到更高的效率,缓存会采取以下数据加载机制:
- 缓存行:缓存不是单个字节地存储与加载数据,而是以缓存行为单位。相比于单个字节的传输,缓存行的传输形式更加高效。
- 预取机制:处理器会尝试预测数据访问模式(例如顺序访问、固定步长跳跃访问等),并根据特定模式将数据加载至缓存之中,从而提升命中率。
- 空间局部性:如果一个数据被访问,那么它附近的数据可能近期也会被访问。因此,缓存在加载某一数据时,也会加载其附近的数据,以提高命中率。
- 时间局部性:如果一个数据被访问,那么它在不久的将来很可能再次被访问。缓存利用这一原理,通过保留最近访问过的数据来提高命中率。
**数组和链表对缓存的利用效率是不同的,主要体现在以下几个方面:
- 占用空间:链表元素比数组元素占用空间更多,导致缓存中容纳的有效数据量更少。
- 缓存行:链表数据分散在内存各处,而缓存是“按行加载”的,因此加载到无效数据的比例更高。
- 预取机制:数组比链表的数据访问模式更具“可预测性”,即系统更容易猜出即将被加载的数据。
- 空间局部性:数组被存储在集中的内存空间中,因此被加载数据附近的数据更有可能即将被访问。
总体而言,数组具有更高的缓存命中率,因此它在操作效率上通常优于链表。这使得在解决算法问题时,基于数组实现的数据结构往往更受欢迎。
需要注意的是,高缓存效率并不意味着数组在所有情况下都优于链表。实际应用中选择哪种数据结构,应根据具体需求来决定
- 在做算法题时,我们会倾向于选择基于数组实现的栈,因为它提供了更高的操作效率和随机访问的能力,代价仅是需要预先为数组分配一定的内存空间。
- 如果数据量非常大、动态性很高、栈的预期大小难以估计,那么基于链表实现的栈更加合适。链表能够将大量数据分散存储于内存的不同部分,并且避免了数组扩容产生的额外开销。
栈和队列
栈
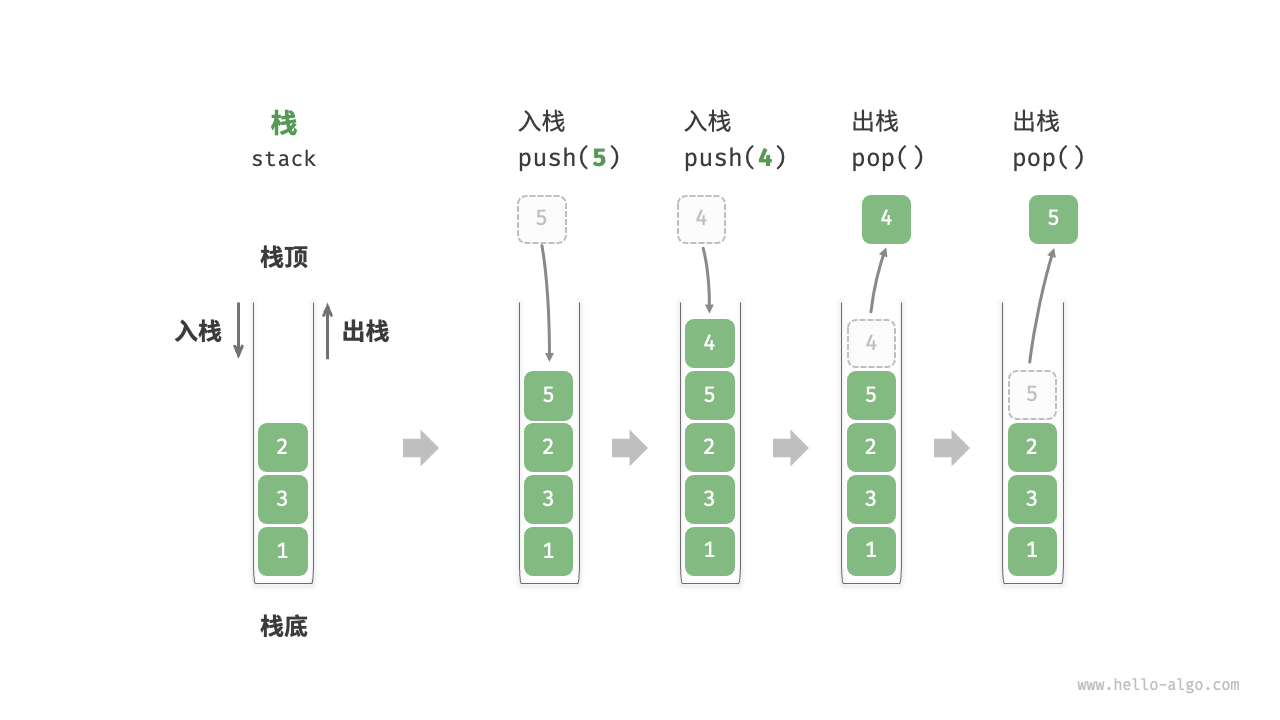
栈stack是一种遵循先入后出的逻辑的线性数据结构
- 堆叠元素的顶部称为栈顶,底部称为栈底
- 把元素添加到栈顶的操作叫作入栈,删除栈顶元素的操作叫作出栈
/* 初始化栈 */
Stack<int> stack = new();
/* 元素入栈 */
stack.Push(1);
stack.Push(2);
stack.Push(3);
stack.Push(4);
stack.Push(5);
/* 访问栈顶元素 */
int peek = stack.Peek();
/* 元素出栈 */
int pop = stack.Pop();
基于链表的实现
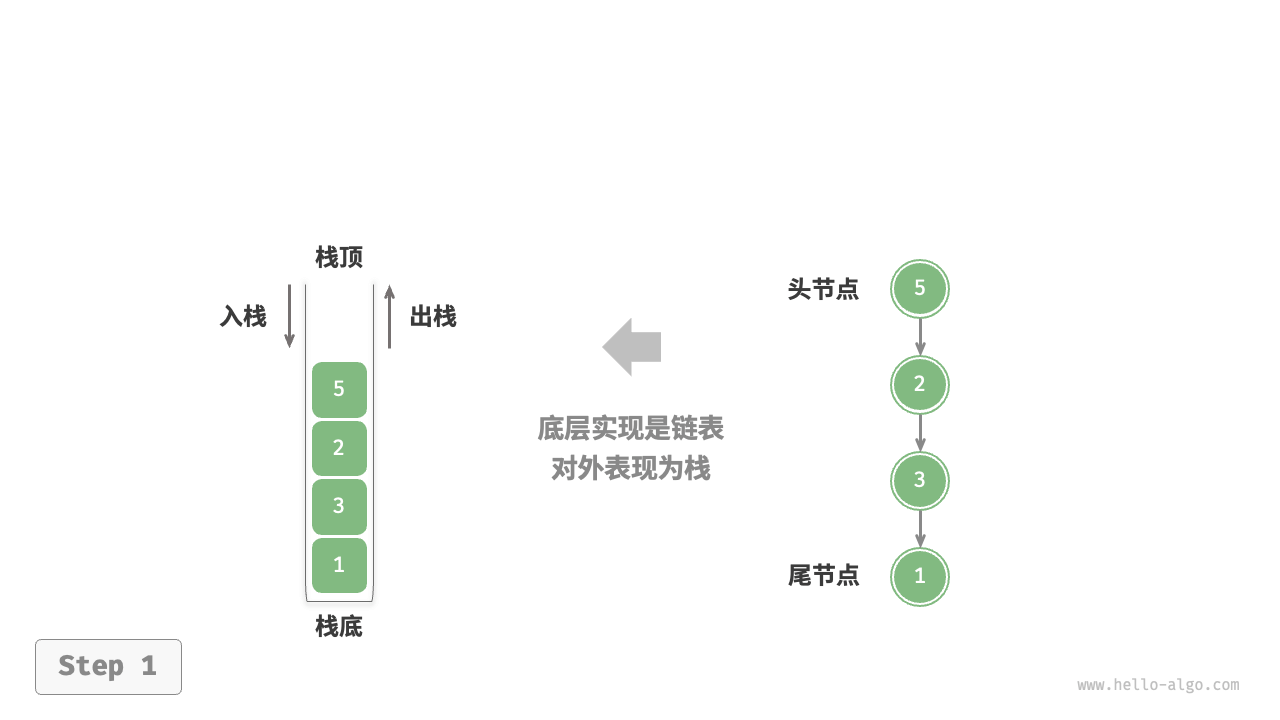
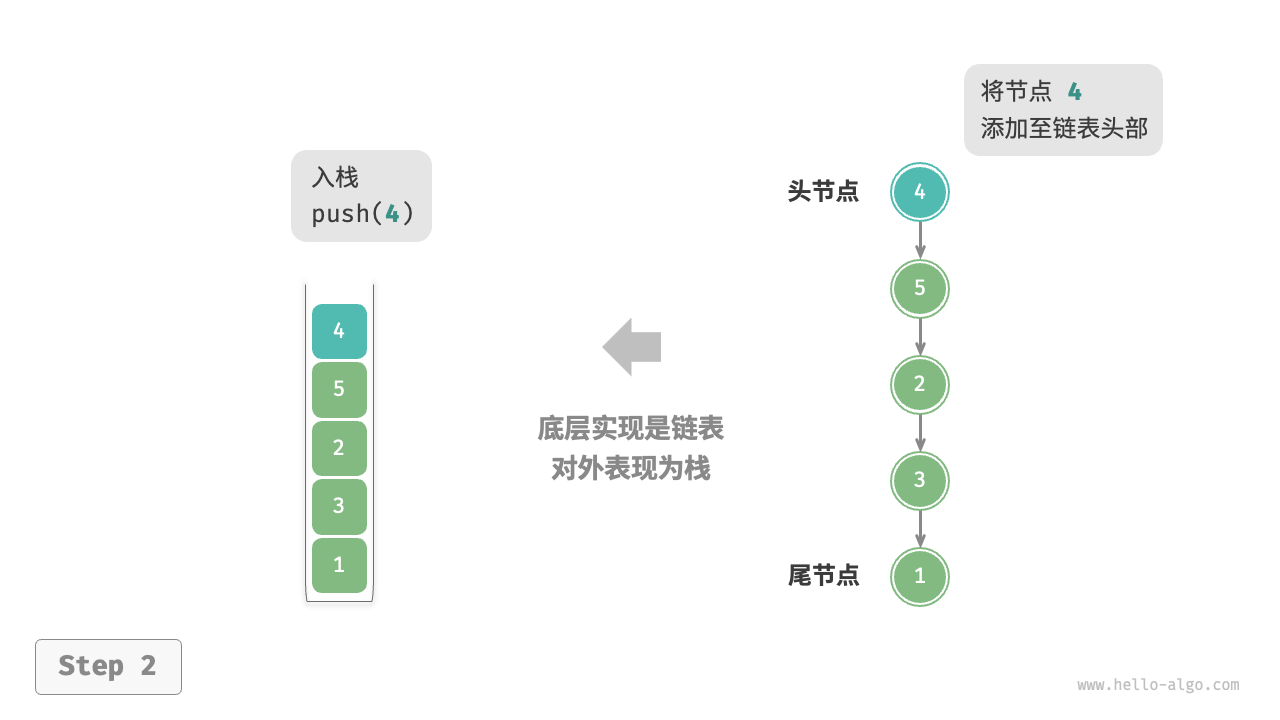
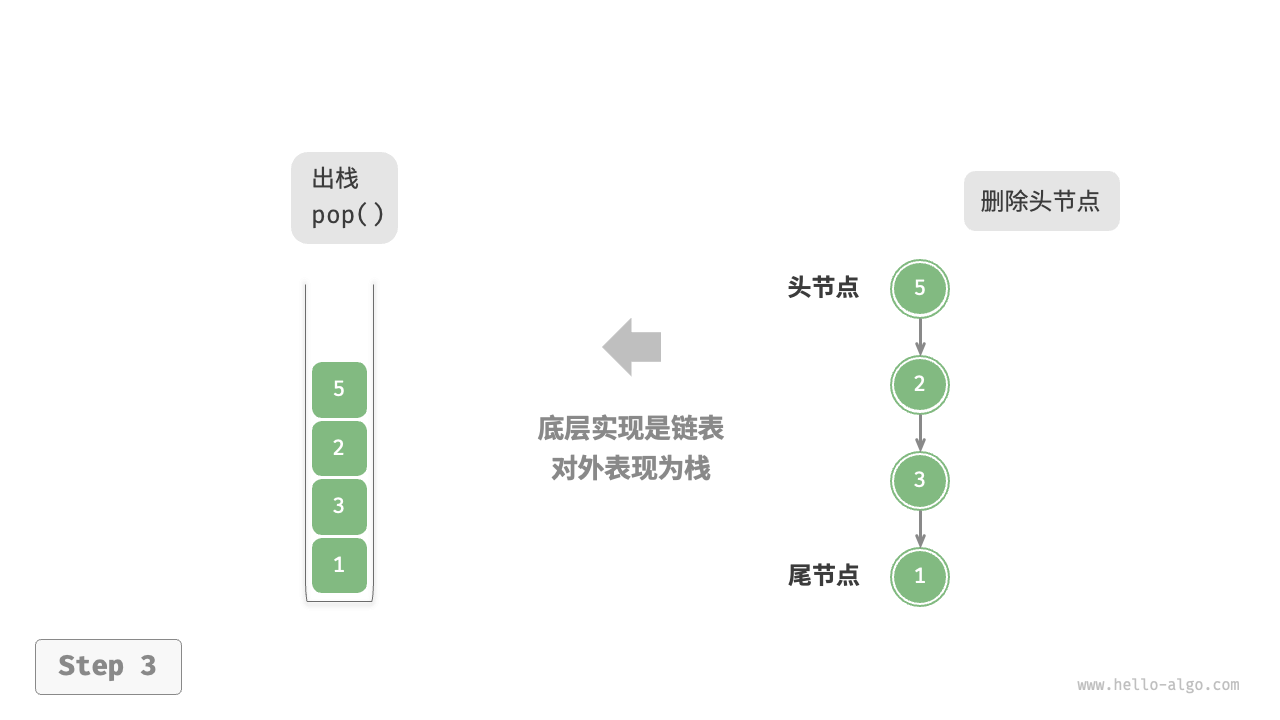
*使用链表实现栈时,我们可以将链表的头节点视为栈顶,尾节点视为栈底
/* 基于链表实现的栈 */
class LinkedListStack {
ListNode? stackPeek; // 将头节点作为栈顶,可空引用类型
int stkSize = 0; // 栈的长度
public LinkedListStack() {
stackPeek = null;
}
/* 获取栈的长度 */
public int Size() {
return stkSize;
}
/* 判断栈是否为空 */
public bool IsEmpty() {
return Size() == 0;
}
/* 入栈 */
public void Push(int num) {
ListNode node = new(num) {
next = stackPeek
};
stackPeek = node;
stkSize++;
}
/* 出栈 */
public int Pop() {
int num = Peek();
stackPeek = stackPeek!.next;//空引用取消检查操作符,告诉编译器你确定stackPeek不会是null,即使它的类型是可空的。这样可以避免空引用异常的编译器警告
stkSize--;
return num;
}
/* 访问栈顶元素 */
public int Peek() {
if (IsEmpty())
throw new Exception();
return stackPeek!.val;
}
/* 将 List 转化为 Array 并返回 */
public int[] ToArray() {
if (stackPeek == null)
return [];
ListNode? node = stackPeek;
int[] res = new int[Size()];
for (int i = res.Length - 1; i >= 0; i--) {
res[i] = node!.val;
node = node.next;
}
return res;
}
}
基于动态数组的实现
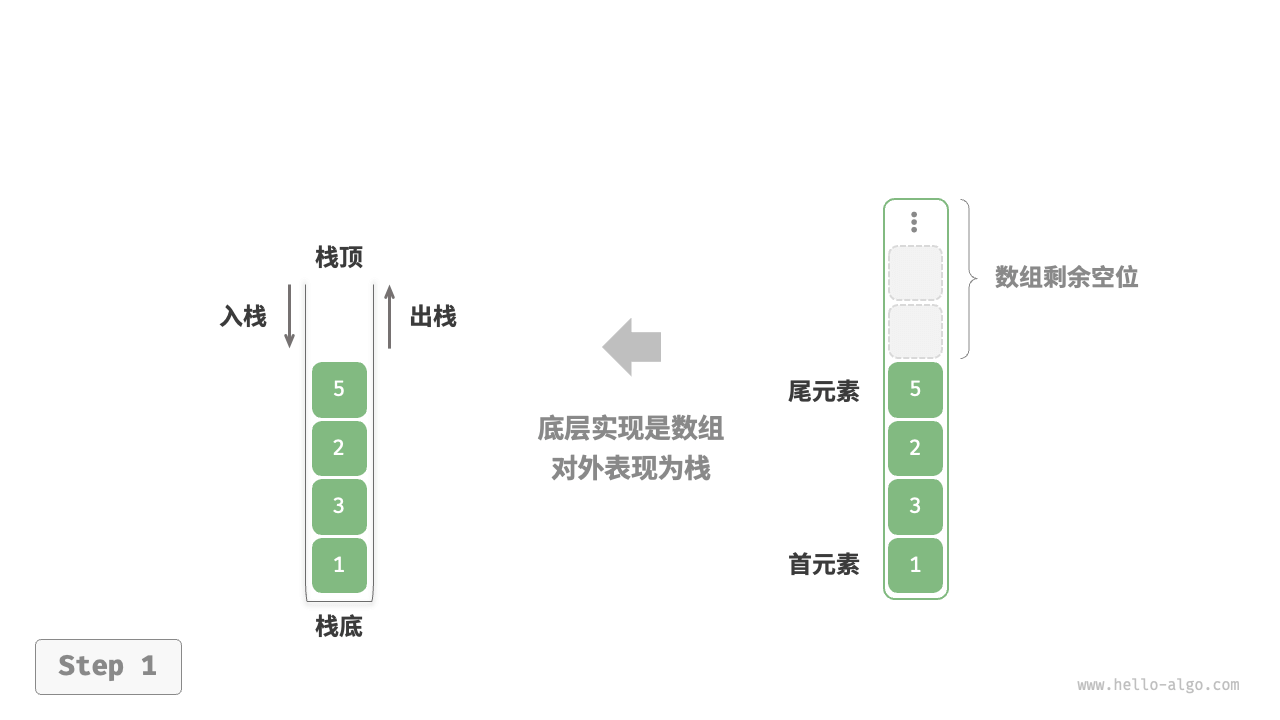
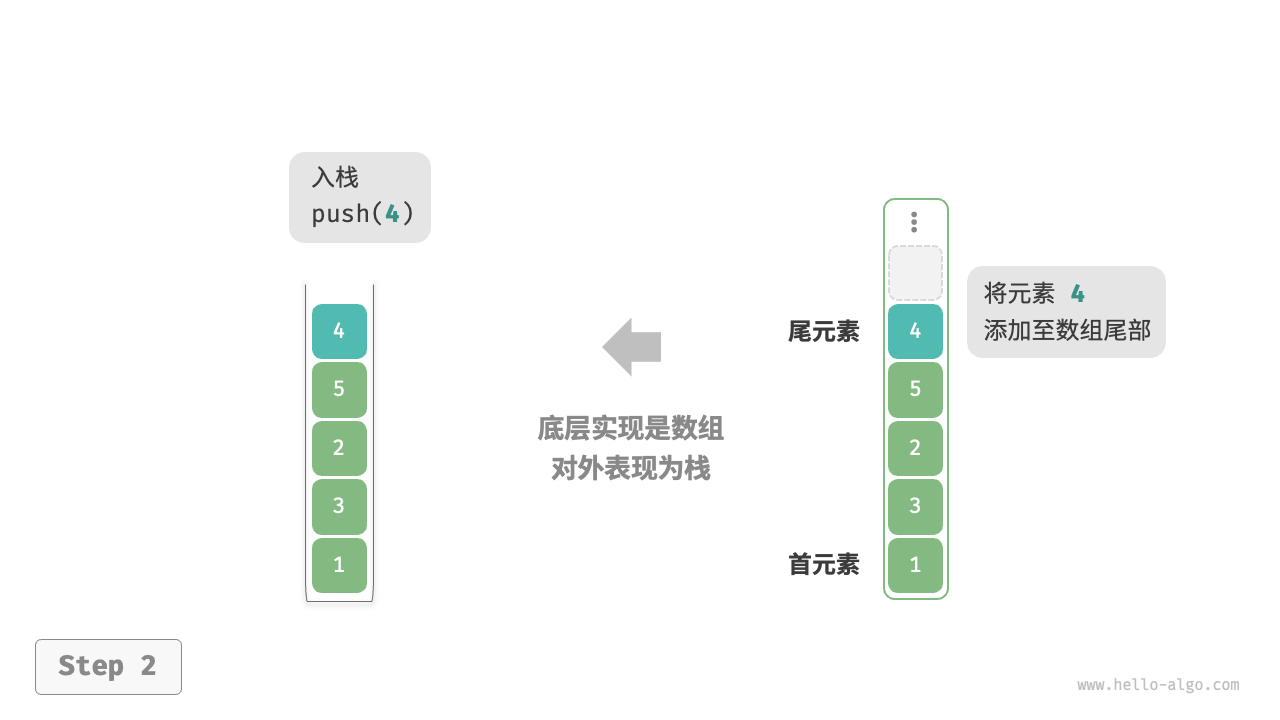
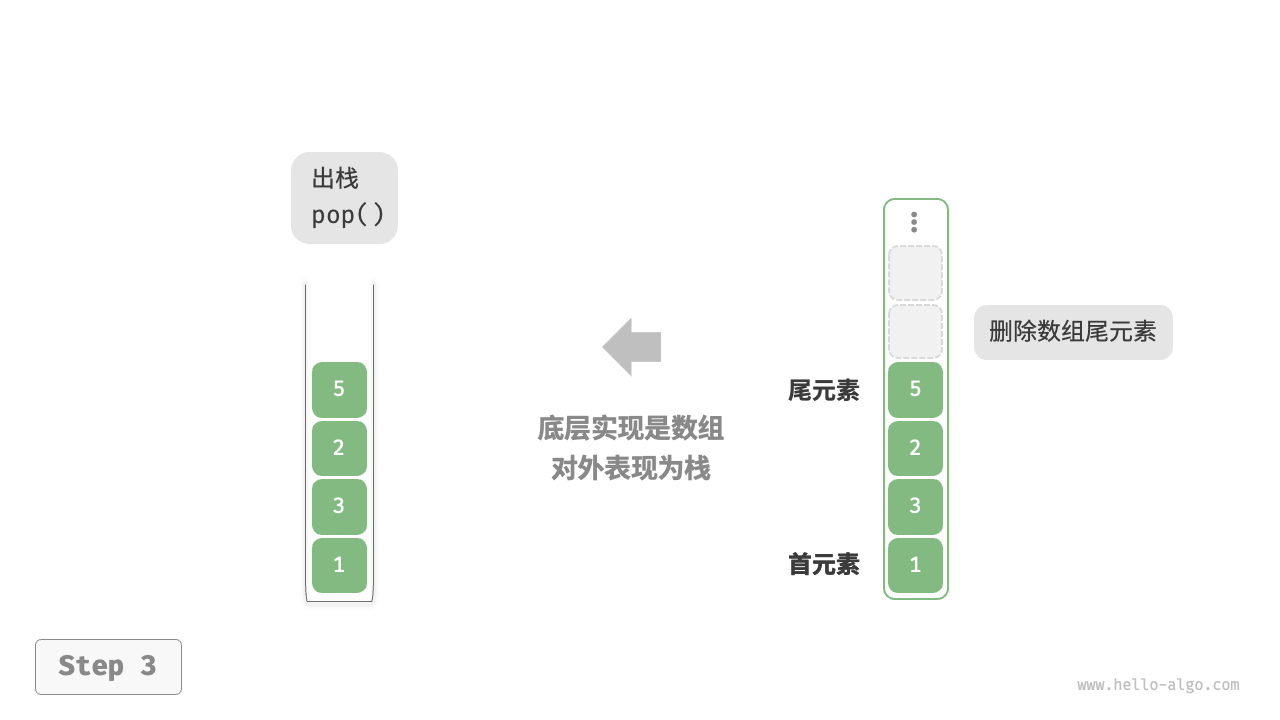
*使用数组实现栈时,可以将数组的尾部作为栈顶。入栈与出栈操作分别对应在数组尾部添加元素与删除元素,时间复杂度都为 O(1)
/* 基于动态数组实现的栈 */
class ArrayStack {
List<int> stack;
public ArrayStack() {
stack = [];
}
/* 获取栈的长度 */
public int Size() {
return stack.Count;
}
/* 判断栈是否为空 */
public bool IsEmpty() {
return Size() == 0;
}
/* 入栈 */
public void Push(int num) {
stack.Add(num);
}
/* 出栈 */
public int Pop() {
if (IsEmpty())
throw new Exception();
var val = Peek();
stack.RemoveAt(Size() - 1);
return val;
}
/* 访问栈顶元素 */
public int Peek() {
if (IsEmpty())
throw new Exception();
return stack[Size() - 1];
}
/* 将 List 转化为 Array 并返回 */
public int[] ToArray() {
return [.. stack];
}
}
时间效率
- 在基于数组的实现中,入栈和出栈操作都在预先分配好的连续内存中进行,具有很好的缓存本地性,因此效率较高。然而,如果入栈时超出数组容量,会触发扩容机制,导致该次入栈操作的时间复杂度变为 O(n)
- 在基于链表的实现中,链表的扩容非常灵活,不存在上述数组扩容时效率降低的问题。但是,入栈操作需要初始化节点对象并修改指针,因此效率相对较低。不过,如果入栈元素本身就是节点对象,那么可以省去初始化步骤,从而提高效率。
- 基于数组实现的栈在触发扩容时效率会降低,但由于扩容是低频操作,因此平均效率更高
- 基于链表实现的栈可以提供更加稳定的效率表现
空间效率
- 基于数组实现的栈可能造成一定的空间浪费
- 由于链表节点需要额外存储指针,因此链表节点占用的空间相对较大
*栈的典型应用
- 浏览器中的后退与前进、软件中的撤销与反撤销。每当我们打开新的网页,浏览器就会对上一个网页执行入栈,这样我们就可以通过后退操作回到上一个网页。后退操作实际上是在执行出栈。如果要同时支持后退和前进,那么需要两个栈来配合实现
- 程序内存管理。每次调用函数时,系统都会在栈顶添加一个栈帧,用于记录函数的上下文信息。在递归函数中,向下递推阶段会不断执行入栈操作,而向上回溯阶段则会不断执行出栈操作
队列
队列queue是一种遵循先入先出规则的线性数据结构
- 堆叠元素的顶部称为队首,底部称为队尾
- 把元素添加到队尾的操作叫作入队,删除队首元素的操作叫作出队
![]()
/* 初始化队列 */
Queue<int> queue = new();
/* 元素入队 */
queue.Enqueue(1);
queue.Enqueue(3);
queue.Enqueue(2);
queue.Enqueue(5);
queue.Enqueue(4);
/* 访问队首元素 */
int peek = queue.Peek();
/* 元素出队 */
int pop = queue.Dequeue();
/* 获取队列的长度 */
int size = queue.Count;
基于链表的实现
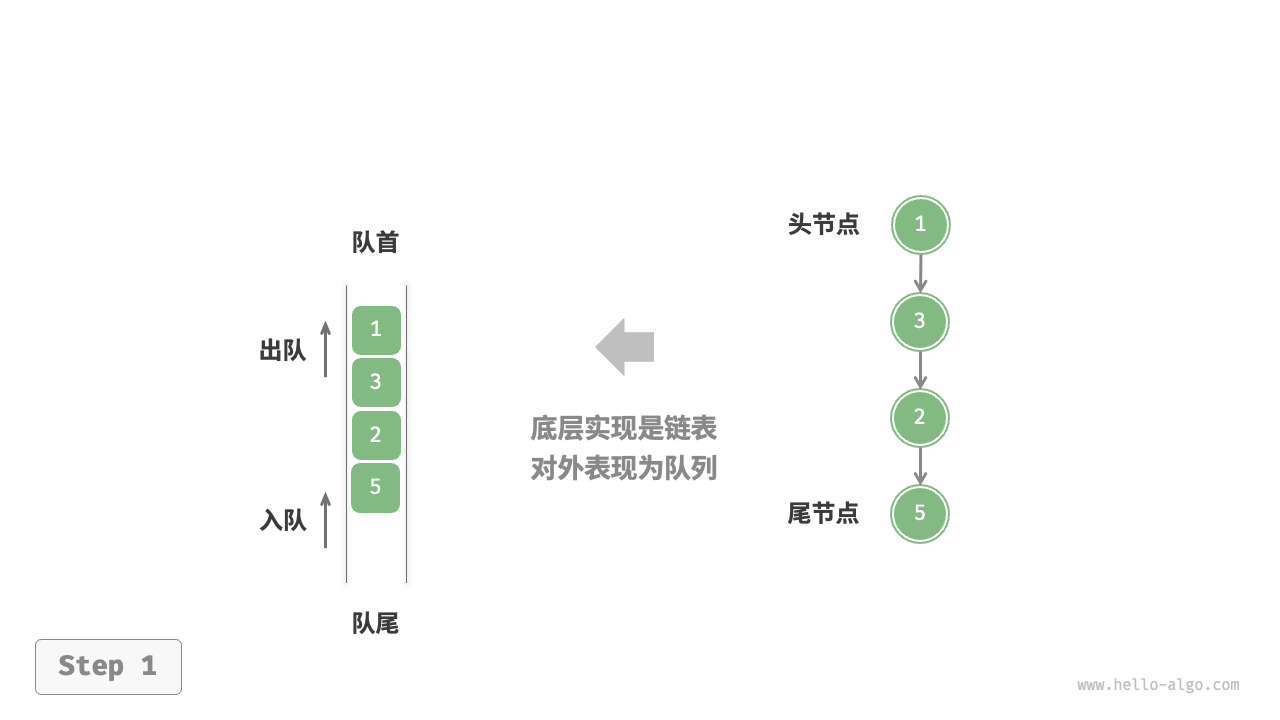
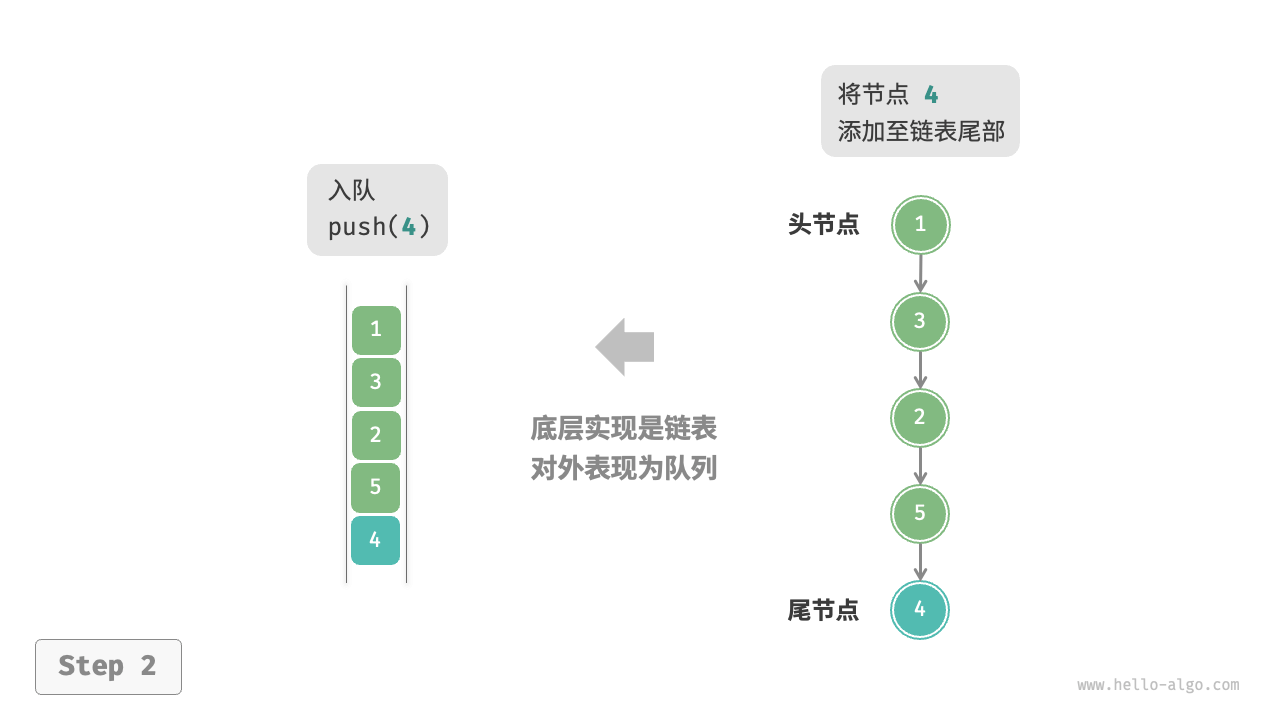
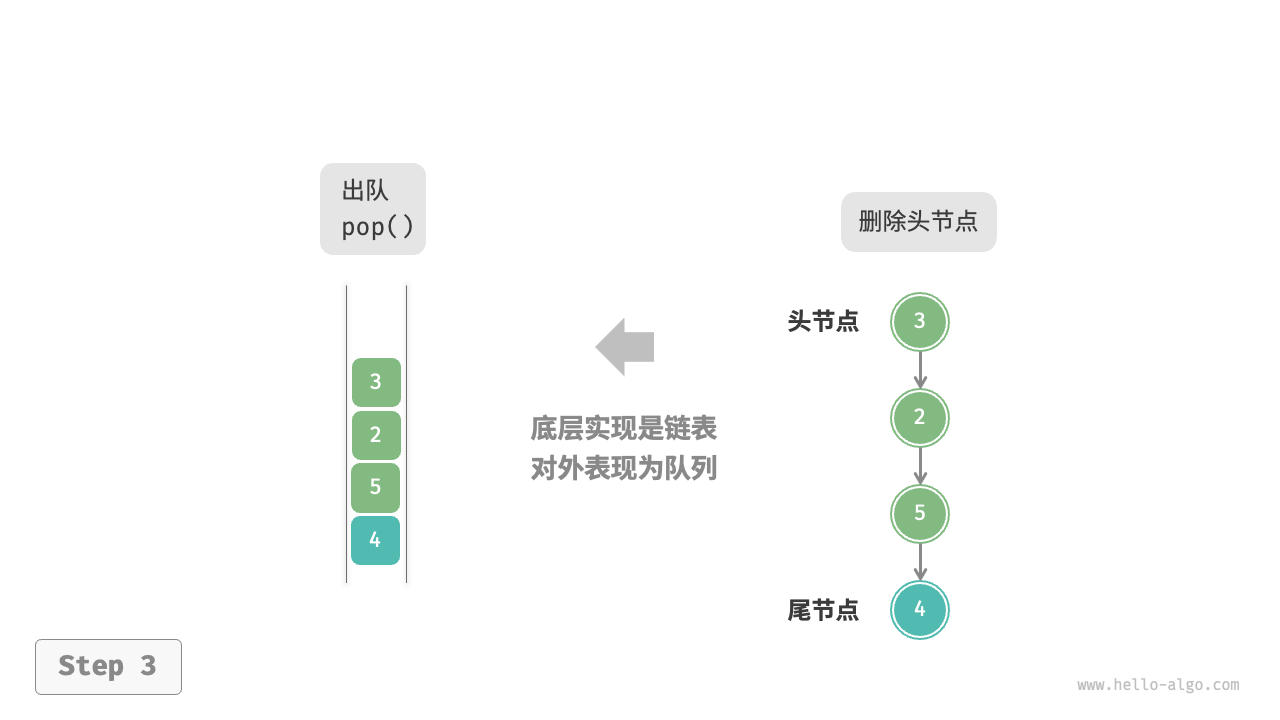
/* 基于链表实现的队列 */
class LinkedListQueue {
ListNode? front, rear; // 头节点 front ,尾节点 rear
int queSize = 0;
public LinkedListQueue() {
front = null;
rear = null;
}
/* 获取队列的长度 */
public int Size() {
return queSize;
}
/* 判断队列是否为空 */
public bool IsEmpty() {
return Size() == 0;
}
/* 入队 */
public void Push(int num) {
// 在尾节点后添加 num
ListNode node = new(num);
// 如果队列为空,则令头、尾节点都指向该节点
if (front == null) {
front = node;
rear = node;
// 如果队列不为空,则将该节点添加到尾节点后
} else if (rear != null) {
rear.next = node;
rear = node;
}
queSize++;
}
/* 出队 */
public int Pop() {
int num = Peek();
// 删除头节点
front = front?.next;
queSize--;
return num;
}
/* 访问队首元素 */
public int Peek() {
if (IsEmpty())
throw new Exception();
return front!.val;
}
/* 将链表转化为 Array 并返回 */
public int[] ToArray() {
if (front == null)
return [];
ListNode? node = front;
int[] res = new int[Size()];
for (int i = 0; i < res.Length; i++) {
res[i] = node!.val;
node = node.next;
}
return res;
}
}
基于数组的实现
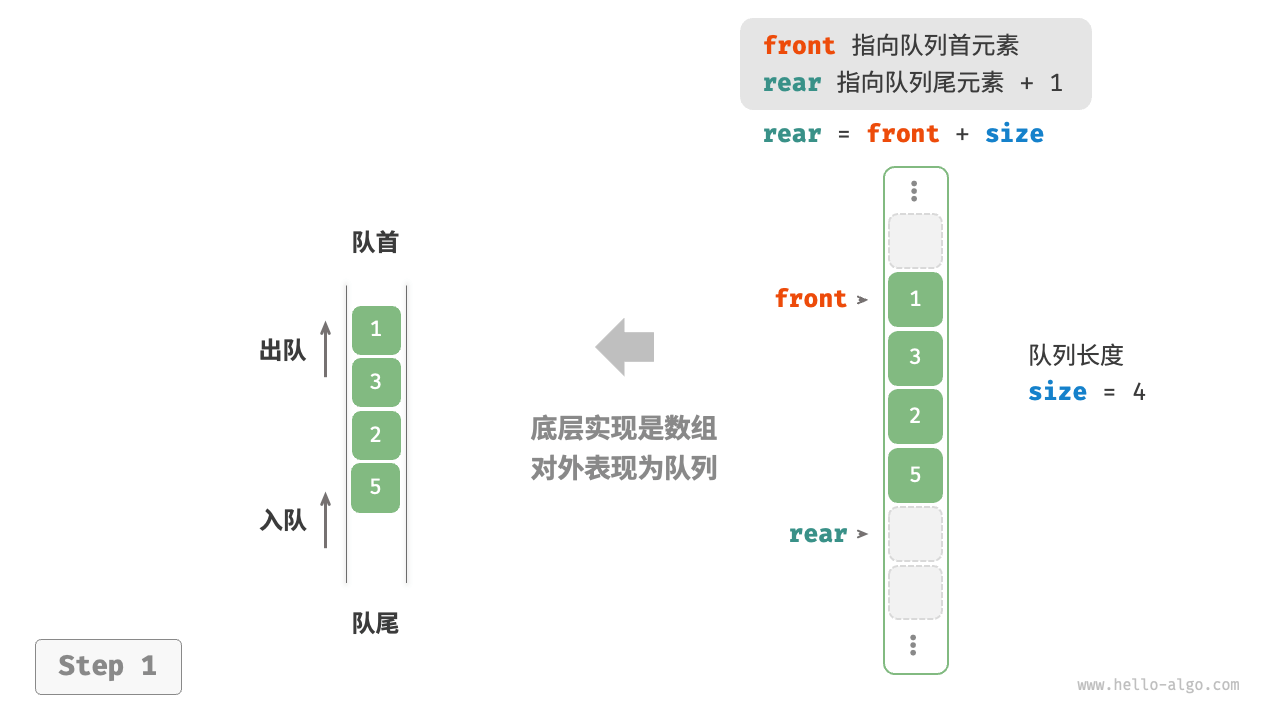
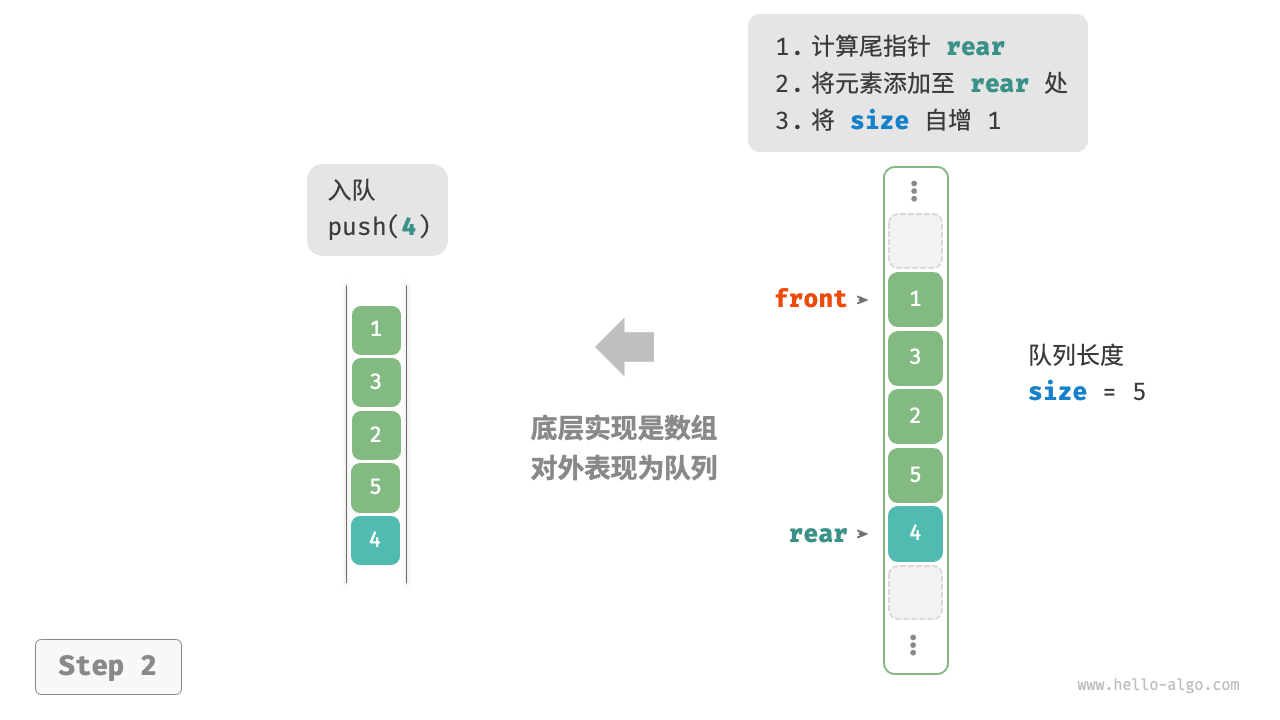
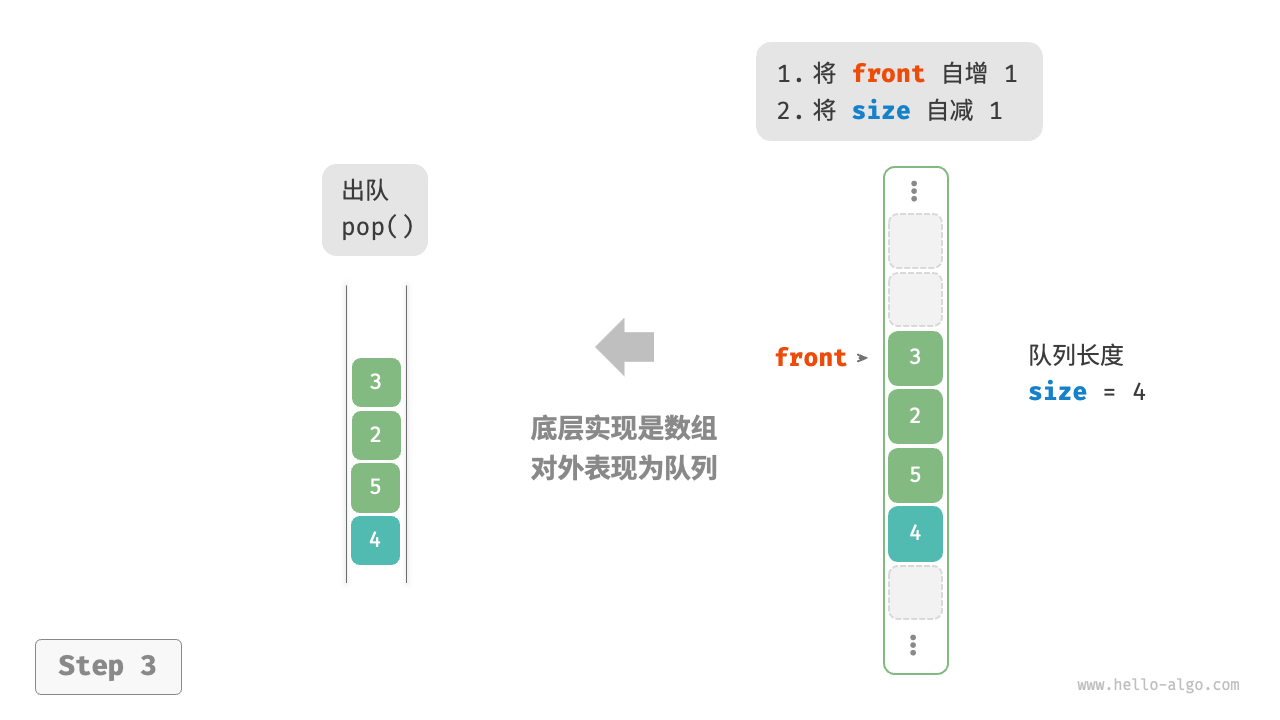
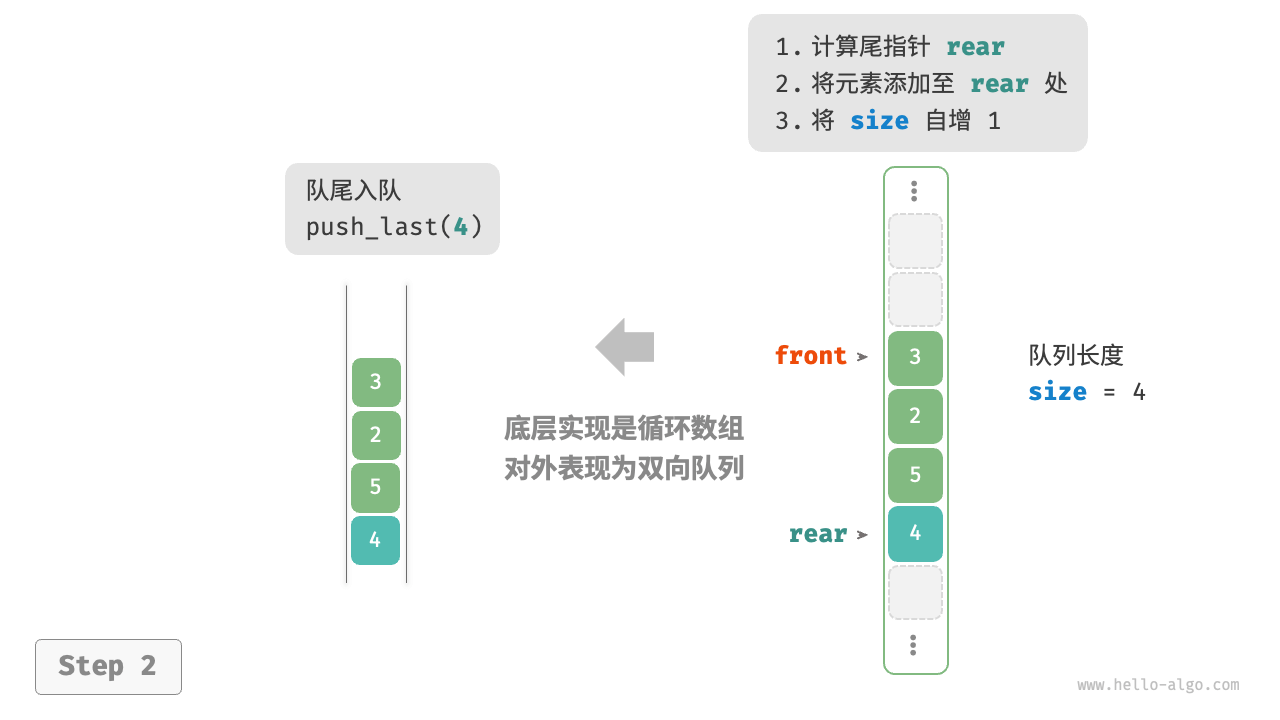
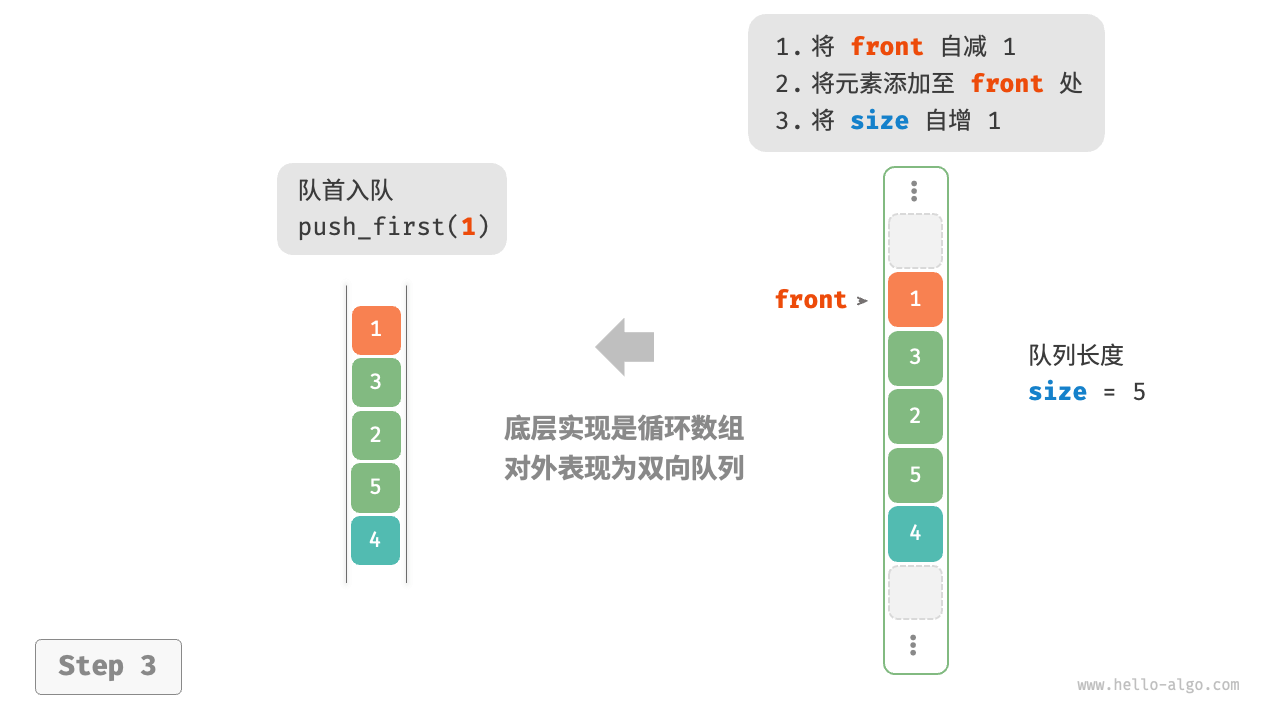
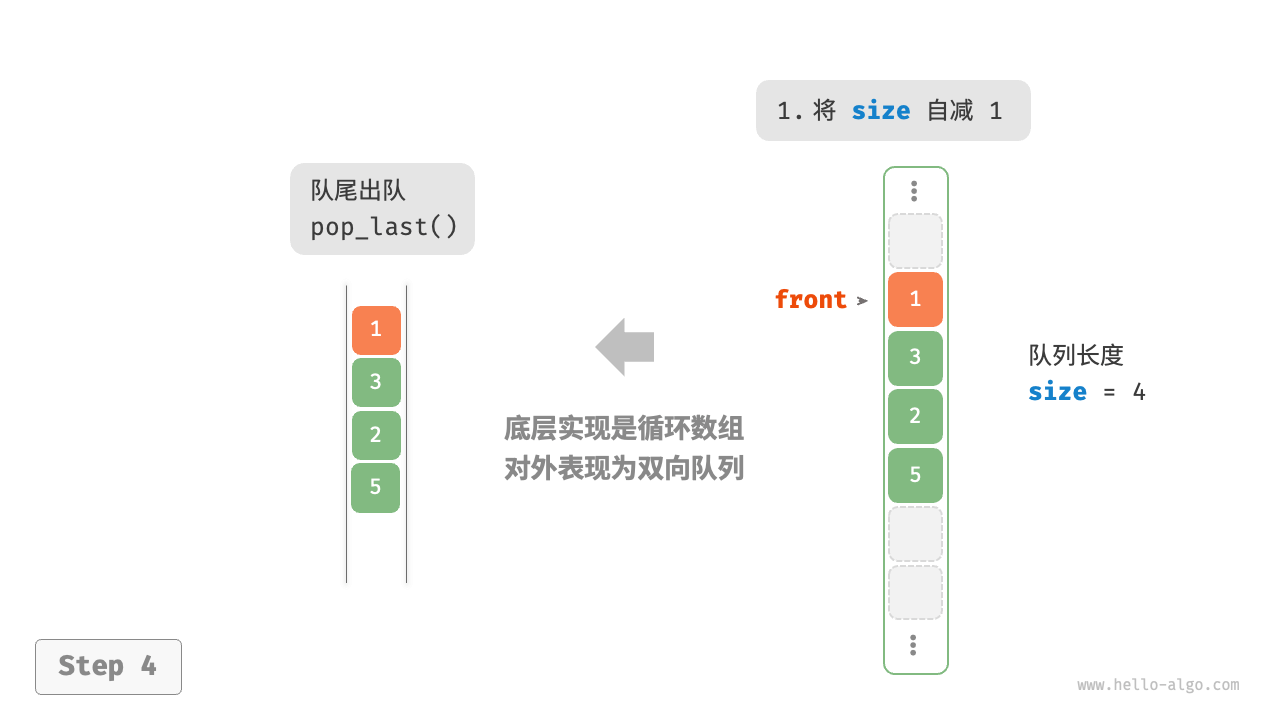
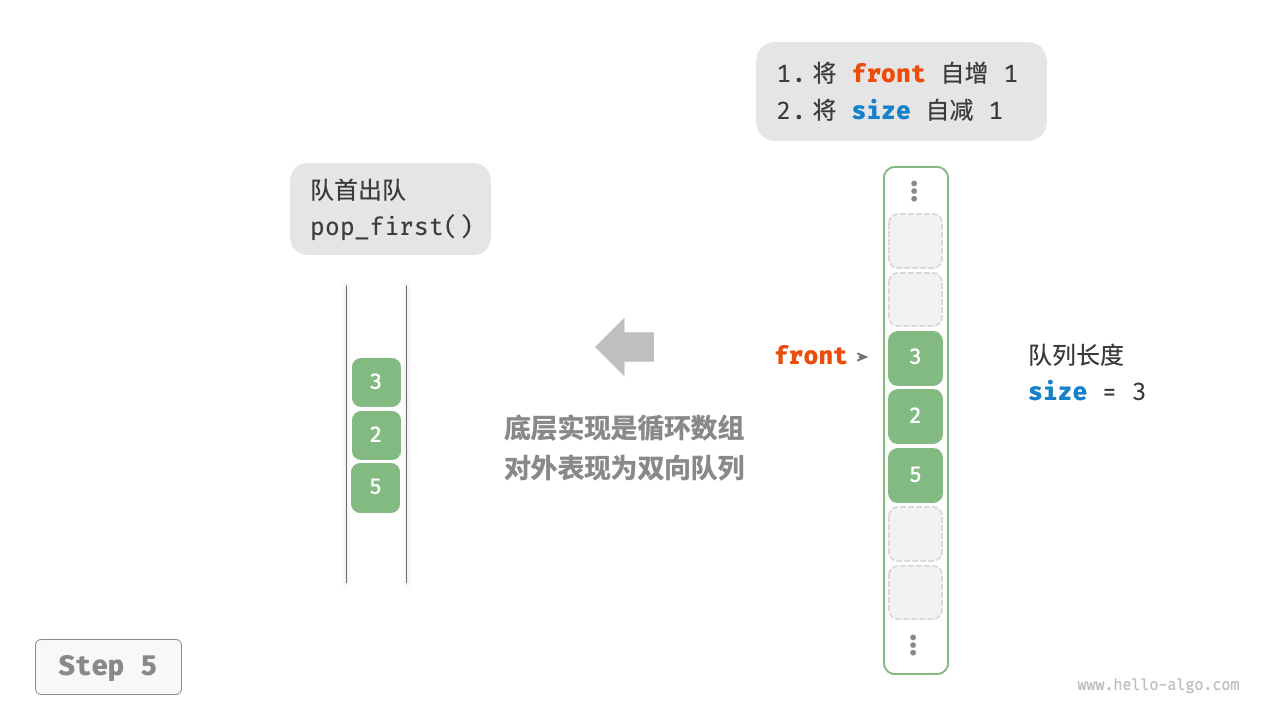
在数组中删除首元素的时间复杂度为 O(n) ,这会导致出队操作效率较低。可以采用以下巧妙方法来避免这个问题:
我们可以使用一个变量 front 指向队首元素的索引,并维护一个变量 size 用于记录队列长度。定义 rear = front + size ,这个公式计算出的 rear 指向队尾元素之后的下一个位置
基于此设计,数组中包含元素的有效区间为 [front, rear - 1]
- 入队操作:将输入元素赋值给
rear索引处,并将size增加 1 - 出队操作:只需将
front增加 1 ,并将size减少 1
入队和出队操作都只需进行一次操作,时间复杂度均为 O(1)
在不断进行入队和出队的过程中,front 和 rear 都在向右移动,当它们到达数组尾部时就无法继续移动。为了解决此问题,我们可以将数组视为首尾相接的环形数组。
对于环形数组,我们需要让 front 或 rear 在越过数组尾部时,直接回到数组头部继续遍历。这种周期性规律可以通过“取余操作”来实现
/* 基于环形数组实现的队列 */
class ArrayQueue {
int[] nums; // 用于存储队列元素的数组
int front; // 队首指针,指向队首元素
int queSize; // 队列长度
public ArrayQueue(int capacity) {
nums = new int[capacity];
front = queSize = 0;
}
/* 获取队列的容量 */
int Capacity() {
return nums.Length;
}
/* 获取队列的长度 */
public int Size() {
return queSize;
}
/* 判断队列是否为空 */
public bool IsEmpty() {
return queSize == 0;
}
/* 入队 */
public void Push(int num) {
if (queSize == Capacity()) {
Console.WriteLine("队列已满");
return;
}
// 计算队尾指针,指向队尾索引 + 1
// 通过取余操作实现 rear 越过数组尾部后回到头部
int rear = (front + queSize) % Capacity();
// 将 num 添加至队尾
nums[rear] = num;
queSize++;
}
/* 出队 */
public int Pop() {
int num = Peek();
// 队首指针向后移动一位,若越过尾部,则返回到数组头部
front = (front + 1) % Capacity();
queSize--;
return num;
}
/* 访问队首元素 */
public int Peek() {
if (IsEmpty())
throw new Exception();
return nums[front];
}
/* 返回数组 */
public int[] ToArray() {
// 仅转换有效长度范围内的列表元素
int[] res = new int[queSize];
for (int i = 0, j = front; i < queSize; i++, j++) {
res[i] = nums[j % this.Capacity()];
}
return res;
}
}
*队列典型应用
- 淘宝订单。购物者下单后,订单将加入队列中,系统随后会根据顺序处理队列中的订单。在双十一期间,短时间内会产生海量订单,高并发成为工程师们需要重点攻克的问题。
- 各类待办事项。任何需要实现“先来后到”功能的场景,例如打印机的任务队列、餐厅的出餐队列等,队列在这些场景中可以有效地维护处理顺序
双向队列
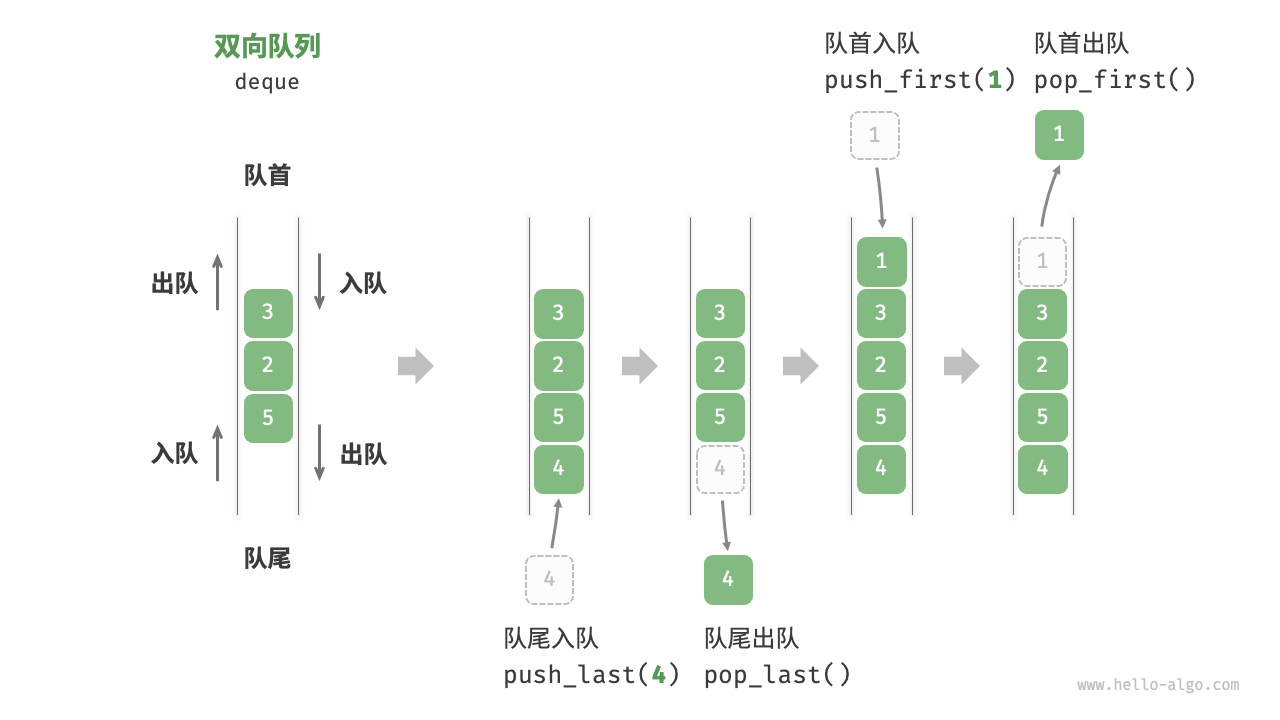
/* 初始化双向队列 */
// 在 C# 中,将链表 LinkedList 看作双向队列来使用
LinkedList<int> deque = new();
/* 元素入队 */
deque.AddLast(2); // 添加至队尾
deque.AddLast(5);
deque.AddLast(4);
deque.AddFirst(3); // 添加至队首
deque.AddFirst(1);
/* 访问元素 */
int peekFirst = deque.First.Value; // 队首元素
int peekLast = deque.Last.Value; // 队尾元素
/* 元素出队 */
deque.RemoveFirst(); // 队首元素出队
deque.RemoveLast(); // 队尾元素出队
/* 获取双向队列的长度 */
int size = deque.Count;
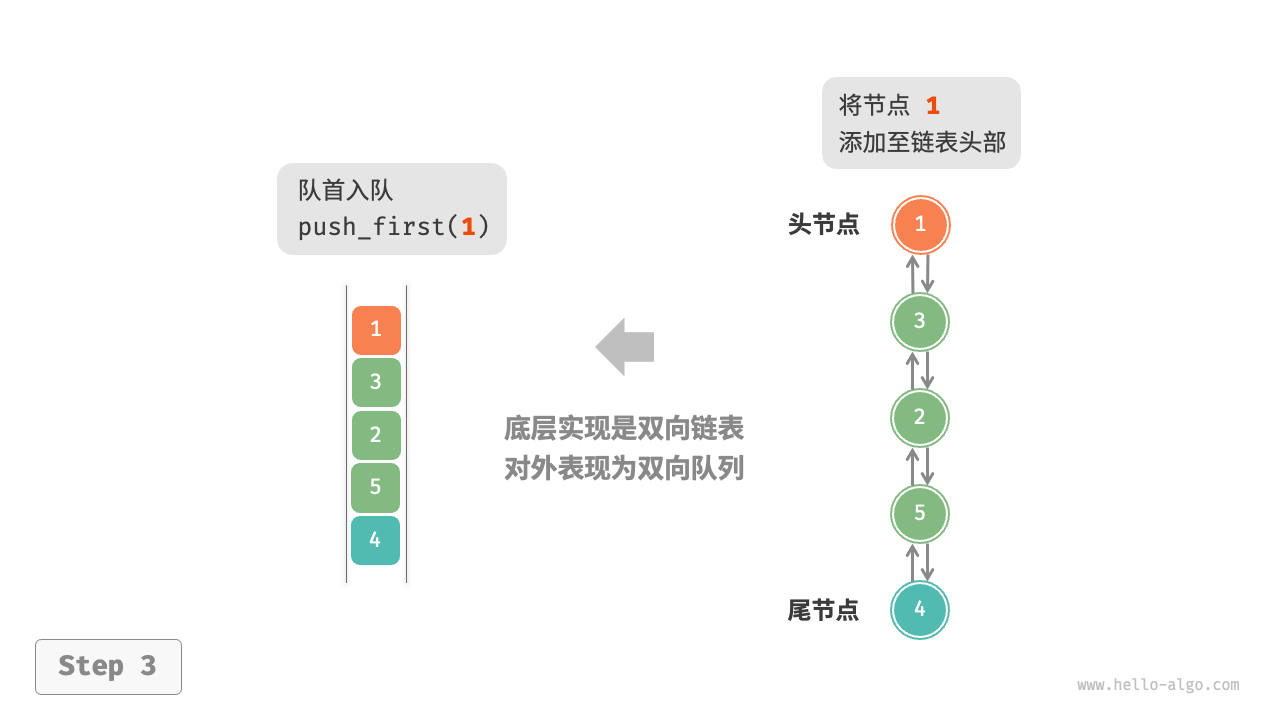
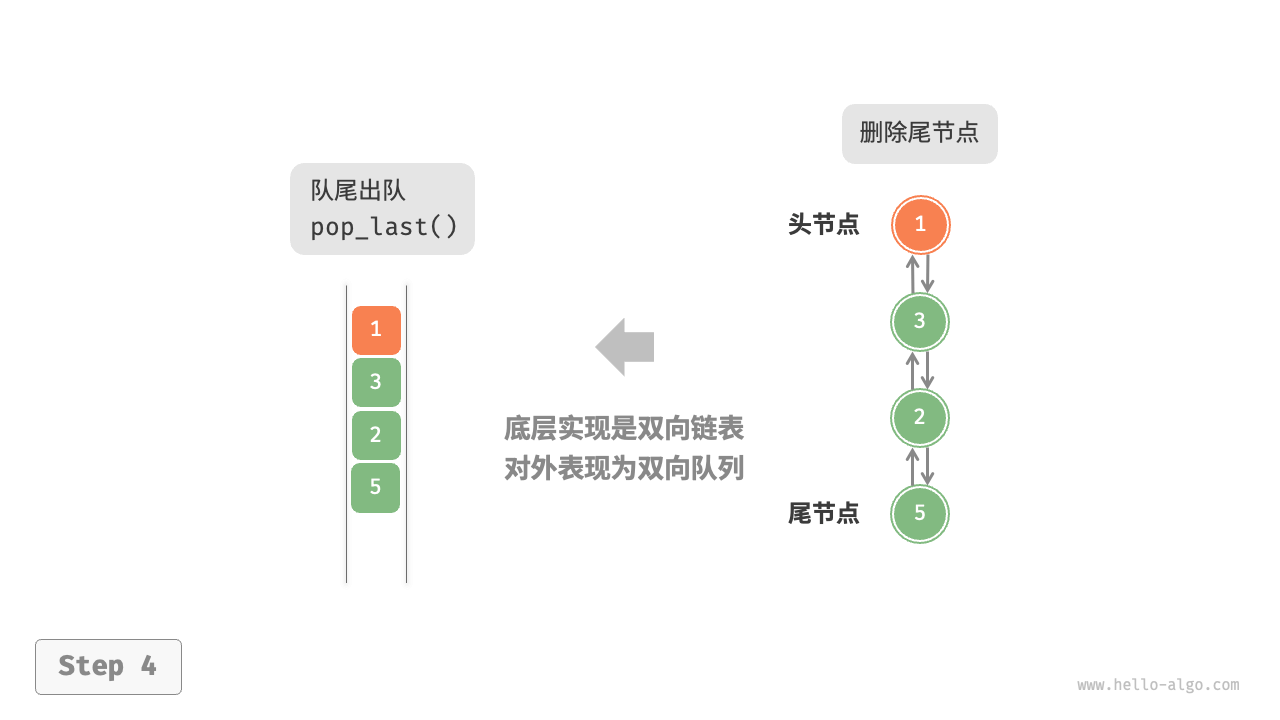
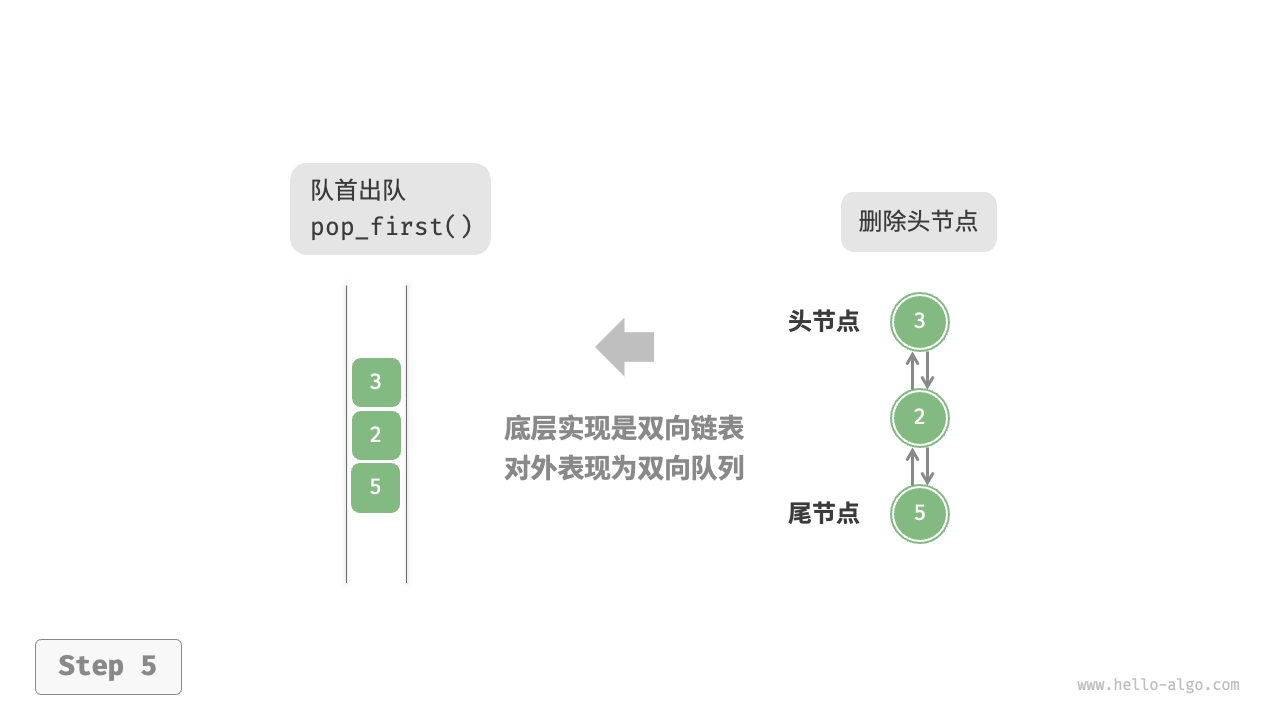
基于双向链表的实现
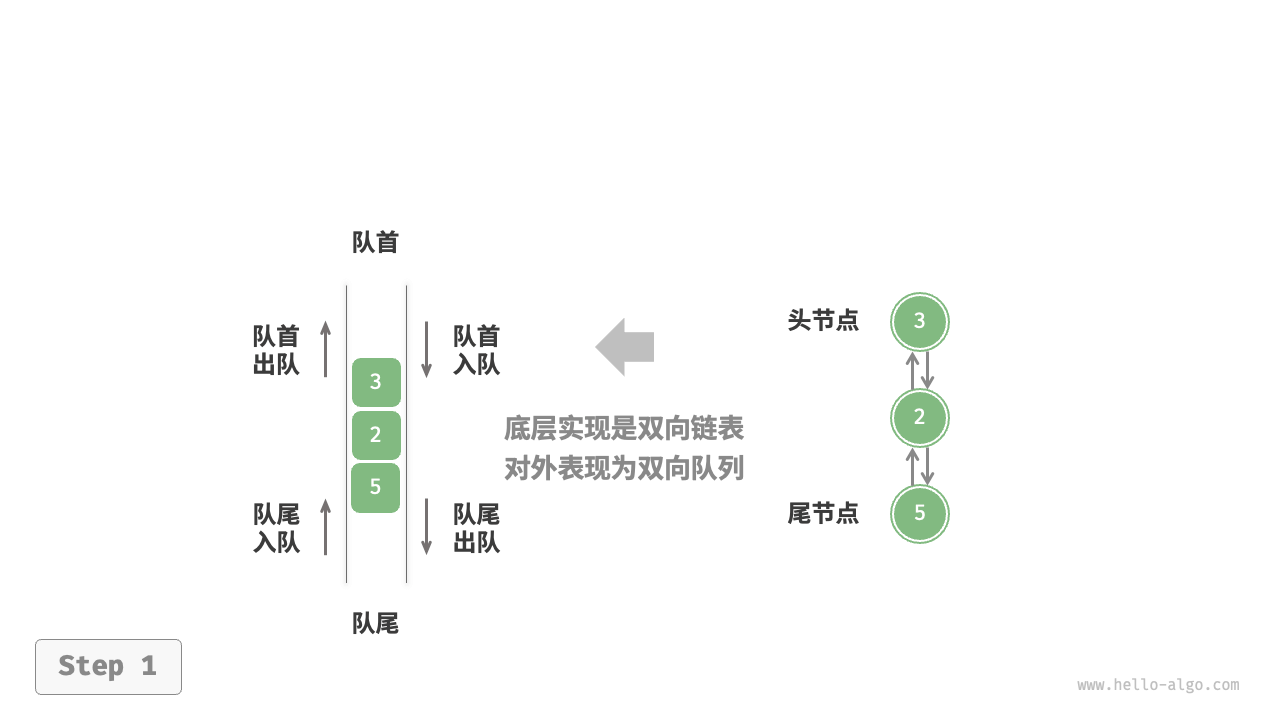
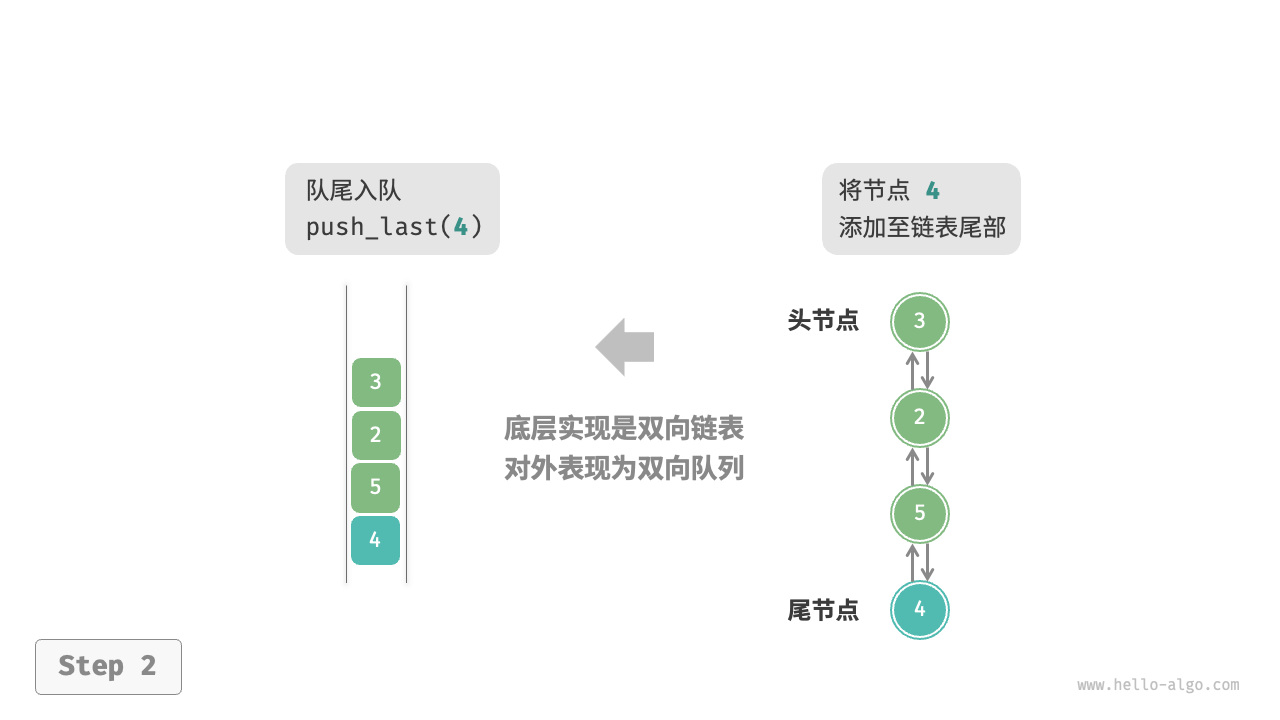
/* 双向链表节点 */
class ListNode(int val) {
public int val = val; // 节点值
public ListNode? prev = null; // 前驱节点引用
public ListNode? next = null; // 后继节点引用
}
/* 基于双向链表实现的双向队列 */
class LinkedListDeque {
ListNode? front, rear; // 头节点 front, 尾节点 rear
int queSize = 0; // 双向队列的长度
public LinkedListDeque() {
front = null;
rear = null;
}
/* 获取双向队列的长度 */
public int Size() {
return queSize;
}
/* 判断双向队列是否为空 */
public bool IsEmpty() {
return Size() == 0;
}
/* 入队操作 */
void Push(int num, bool isFront) {
ListNode node = new(num);
// 若链表为空,则令 front 和 rear 都指向 node
if (IsEmpty()) {
front = node;
rear = node;
}
// 队首入队操作
else if (isFront) {
// 将 node 添加至链表头部
front!.prev = node;
node.next = front;
front = node; // 更新头节点
}
// 队尾入队操作
else {
// 将 node 添加至链表尾部
rear!.next = node;
node.prev = rear;
rear = node; // 更新尾节点
}
queSize++; // 更新队列长度
}
/* 队首入队 */
public void PushFirst(int num) {
Push(num, true);
}
/* 队尾入队 */
public void PushLast(int num) {
Push(num, false);
}
/* 出队操作 */
int? Pop(bool isFront) {
if (IsEmpty())
throw new Exception();
int? val;
// 队首出队操作
if (isFront) {
val = front?.val; // 暂存头节点值
// 删除头节点
ListNode? fNext = front?.next;
if (fNext != null) {
fNext.prev = null;
front!.next = null;
}
front = fNext; // 更新头节点
}
// 队尾出队操作
else {
val = rear?.val; // 暂存尾节点值
// 删除尾节点
ListNode? rPrev = rear?.prev;
if (rPrev != null) {
rear!.prev = null;
rPrev.next = null;
}
rear = rPrev; // 更新尾节点
}
queSize--; // 更新队列长度
return val;
}
/* 队首出队 */
public int? PopFirst() {
return Pop(true);
}
/* 队尾出队 */
public int? PopLast() {
return Pop(false);
}
/* 访问队首元素 */
public int? PeekFirst() {
if (IsEmpty())
throw new Exception();
return front?.val;
}
/* 访问队尾元素 */
public int? PeekLast() {
if (IsEmpty())
throw new Exception();
return rear?.val;
}
/* 返回数组用于打印 */
public int?[] ToArray() {
ListNode? node = front;
int?[] res = new int?[Size()];
for (int i = 0; i < res.Length; i++) {
res[i] = node?.val;
node = node?.next;
}
return res;
}
}
基于数组的实现
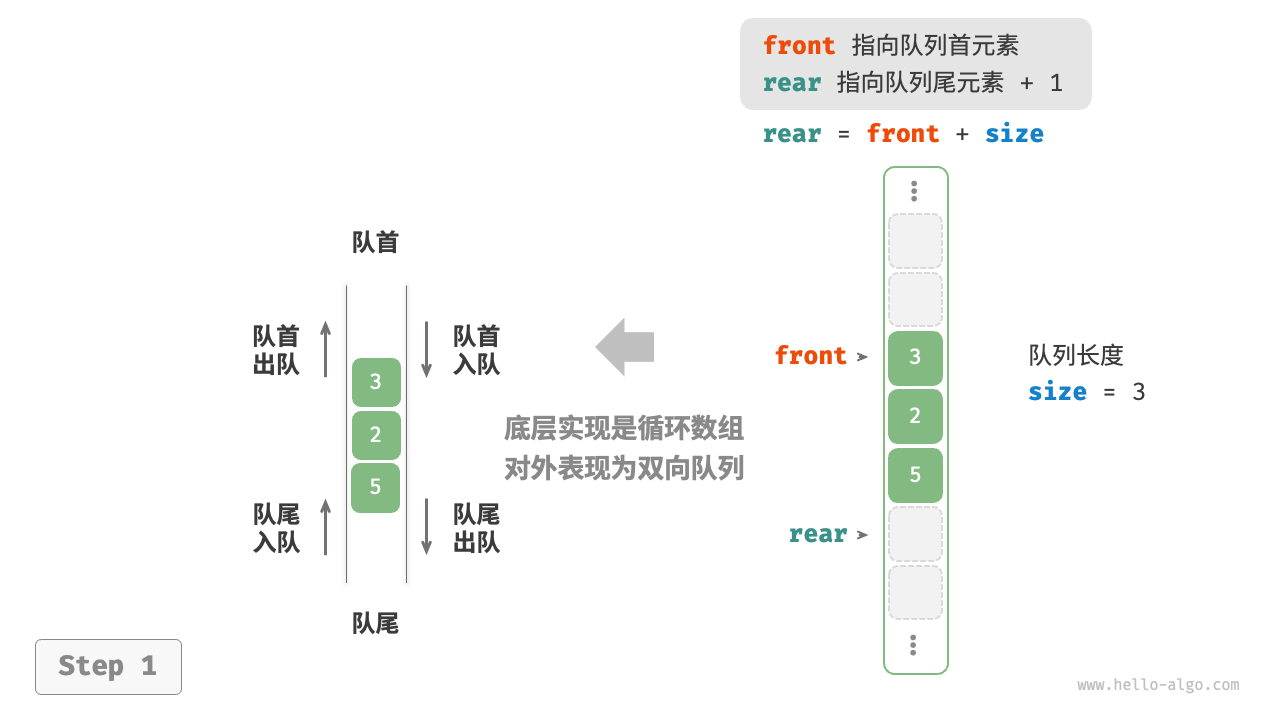
/* 基于环形数组实现的双向队列 */
class ArrayDeque {
int[] nums; // 用于存储双向队列元素的数组
int front; // 队首指针,指向队首元素
int queSize; // 双向队列长度
/* 构造方法 */
public ArrayDeque(int capacity) {
nums = new int[capacity];
front = queSize = 0;
}
/* 获取双向队列的容量 */
int Capacity() {
return nums.Length;
}
/* 获取双向队列的长度 */
public int Size() {
return queSize;
}
/* 判断双向队列是否为空 */
public bool IsEmpty() {
return queSize == 0;
}
/* 计算环形数组索引 */
int Index(int i) {
// 通过取余操作实现数组首尾相连
// 当 i 越过数组尾部后,回到头部
// 当 i 越过数组头部后,回到尾部
return (i + Capacity()) % Capacity();
}
/* 队首入队 */
public void PushFirst(int num) {
if (queSize == Capacity()) {
Console.WriteLine("双向队列已满");
return;
}
// 队首指针向左移动一位
// 通过取余操作实现 front 越过数组头部后回到尾部
front = Index(front - 1);
// 将 num 添加至队首
nums[front] = num;
queSize++;
}
/* 队尾入队 */
public void PushLast(int num) {
if (queSize == Capacity()) {
Console.WriteLine("双向队列已满");
return;
}
// 计算队尾指针,指向队尾索引 + 1
int rear = Index(front + queSize);
// 将 num 添加至队尾
nums[rear] = num;
queSize++;
}
/* 队首出队 */
public int PopFirst() {
int num = PeekFirst();
// 队首指针向后移动一位
front = Index(front + 1);
queSize--;
return num;
}
/* 队尾出队 */
public int PopLast() {
int num = PeekLast();
queSize--;
return num;
}
/* 访问队首元素 */
public int PeekFirst() {
if (IsEmpty()) {
throw new InvalidOperationException();
}
return nums[front];
}
/* 访问队尾元素 */
public int PeekLast() {
if (IsEmpty()) {
throw new InvalidOperationException();
}
// 计算尾元素索引
int last = Index(front + queSize - 1);
return nums[last];
}
/* 返回数组用于打印 */
public int[] ToArray() {
// 仅转换有效长度范围内的列表元素
int[] res = new int[queSize];
for (int i = 0, j = front; i < queSize; i++, j++) {
res[i] = nums[Index(j)];
}
return res;
}
}
哈希表
hash table也称散列表,通过建立key与value之间的映射,实现高效的元素查询
**在哈希表中进行增删查改的时间复杂度都是 O(1)
| 数组 | 链表 | 哈希表 | |
|---|---|---|---|
| 查找元素 | O(1) | O(n) | O(1) |
| 添加元素 | O(n) | O(1) | O(1) |
| 删除元素 | O(n) | O(1) | O(1) |
/* 初始化哈希表 */
Dictionary<int, string> map = new() {
/* 添加操作 */
// 在哈希表中添加键值对 (key, value)
{ 12836, "小哈" },
{ 15937, "小啰" },
{ 16750, "小算" },
{ 13276, "小法" },
{ 10583, "小鸭" }
};
/* 查询操作 */
// 向哈希表中输入键 key ,得到值 value
string name = map[15937];
/* 删除操作 */
// 在哈希表中删除键值对 (key, value)
map.Remove(10583);
/* 遍历哈希表 */
// 遍历键值对 Key->Value
foreach (var kv in map) {
Console.WriteLine(kv.Key + " -> " + kv.Value);
}
// 单独遍历键 key
foreach (int key in map.Keys) {
Console.WriteLine(key);
}
// 单独遍历值 value
foreach (string val in map.Values) {
Console.WriteLine(val);
}
使用数组实现哈希表
在哈希表中,将数组中的每个空位称为桶,每个桶可存储一个键值对。因此查询操作就是找到 key 对应的桶,并在桶中获取 value
如何基于 key 定位对应的桶?
这是通过哈希函数实现的。哈希函数的作用是将一个较大的输入空间映射到一个较小的输出空间。在哈希表中,输入空间是所有 key ,输出空间是所有桶(数组索引)。换句话说,输入一个 key ,我们可以通过哈希函数得到该 key 对应的键值对在数组中的存储位置
输入一个 key ,哈希函数的计算过程分为以下两步。
- 通过某种哈希算法计算得到哈希值。
- 将哈希值对桶数量(数组长度)
capacity取模,从而获取该key对应的数组索引index
![]()
/* 键值对 int->string */
class Pair(int key, string val) {
public int key = key;
public string val = val;
}
/* 基于数组实现的哈希表 */
class ArrayHashMap {
List<Pair?> buckets;
public ArrayHashMap() {
// 初始化数组,包含 100 个桶
buckets = [];
for (int i = 0; i < 100; i++) {
buckets.Add(null);
}
}
/* 哈希函数 */
int HashFunc(int key) {
int index = key % 100;
return index;
}
/* 查询操作 */
public string? Get(int key) {
int index = HashFunc(key);
Pair? pair = buckets[index];
if (pair == null) return null;
return pair.val;
}
/* 添加操作 */
public void Put(int key, string val) {
Pair pair = new(key, val);
int index = HashFunc(key);
buckets[index] = pair;
}
/* 删除操作 */
public void Remove(int key) {
int index = HashFunc(key);
// 置为 null ,代表删除
buckets[index] = null;
}
/* 获取所有键值对 */
public List<Pair> PairSet() {
List<Pair> pairSet = [];
foreach (Pair? pair in buckets) {
if (pair != null)
pairSet.Add(pair);
}
return pairSet;
}
/* 获取所有键 */
public List<int> KeySet() {
List<int> keySet = [];
foreach (Pair? pair in buckets) {
if (pair != null)
keySet.Add(pair.key);
}
return keySet;
}
/* 获取所有值 */
public List<string> ValueSet() {
List<string> valueSet = [];
foreach (Pair? pair in buckets) {
if (pair != null)
valueSet.Add(pair.val);
}
return valueSet;
}
/* 打印哈希表 */
public void Print() {
foreach (Pair kv in PairSet()) {
Console.WriteLine(kv.key + " -> " + kv.val);
}
}
}
哈希冲突与扩容
本质上哈希函数是将所有key构成的输入空间映射到数组所有索引构成的输出空间,而输入空间往往远大于输出空间,因此,一定存在多个输入空间对应相同输出的情况
上述示例中的哈希函数,当输入的 key 后两位相同时,哈希函数的输出结果也相同
12836 % 100 = 36
20336 % 100 = 36
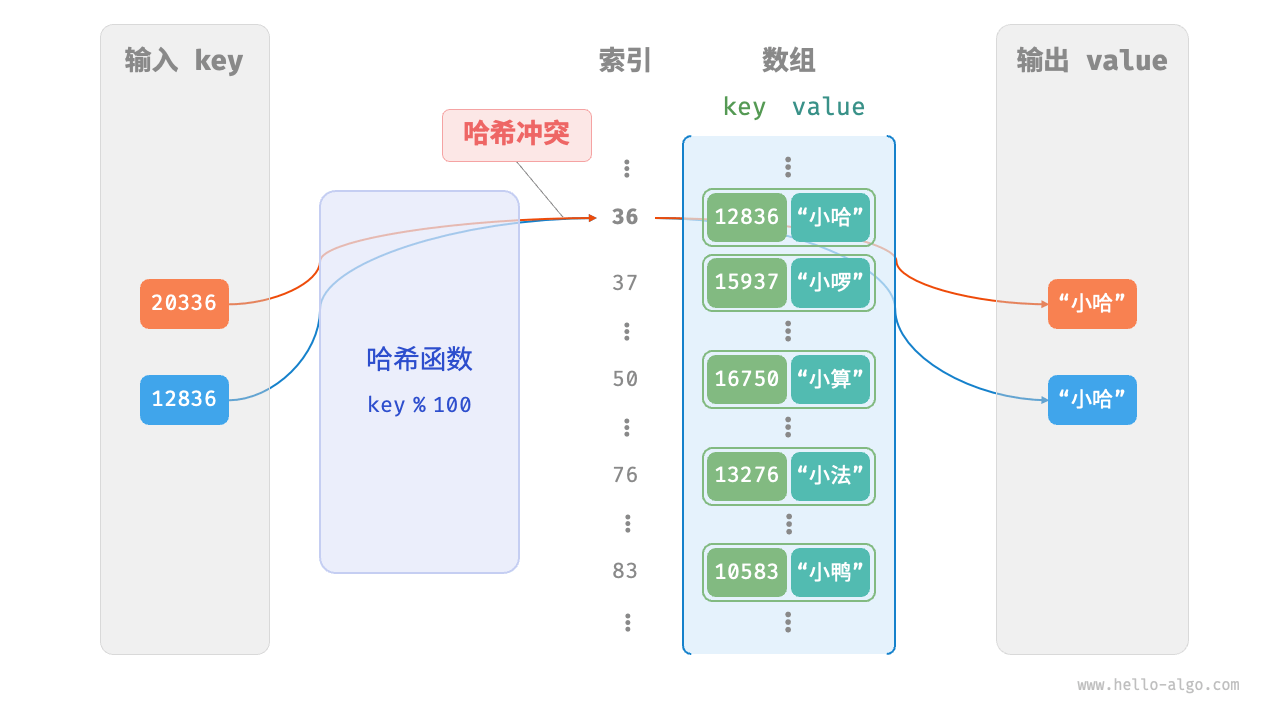
可以通过哈希表扩容来减少哈希冲突

title: 哈希扩容
类似于数组扩容,哈希表扩容需将所有键值对从原哈希表迁移至新哈希表,非常耗时;并且由于哈希表容量 `capacity` 改变,需要通过哈希函数来重新计算所有键值对的存储位置,这进一步增加了扩容过程的计算开销。为此,编程语言通常会预留足够大的哈希表容量,防止频繁扩容。
负载因子(load factor)是哈希表的一个重要概念,其定义为哈希表的元素数量除以桶数量,用于衡量哈希冲突的严重程度,**也常作为哈希表扩容的触发条件**
链式地址
哈希扩容效率低下,为了提升效率,可以采用以下策略。
- 改良哈希表数据结构,使哈希表可以在出现哈希冲突时正常工作。
- 仅在必要时,即当哈希冲突比较严重时,才执行扩容操作。
哈希表的结构改良方法主要包括“链式地址”和“开放寻址"
原始哈希表中,每个桶仅存储一个键值对.链式地址(separate chaining)将单个元素转换为链表,将键值对作为链表节点,将所有发生冲突的键值对存储在同一链表中
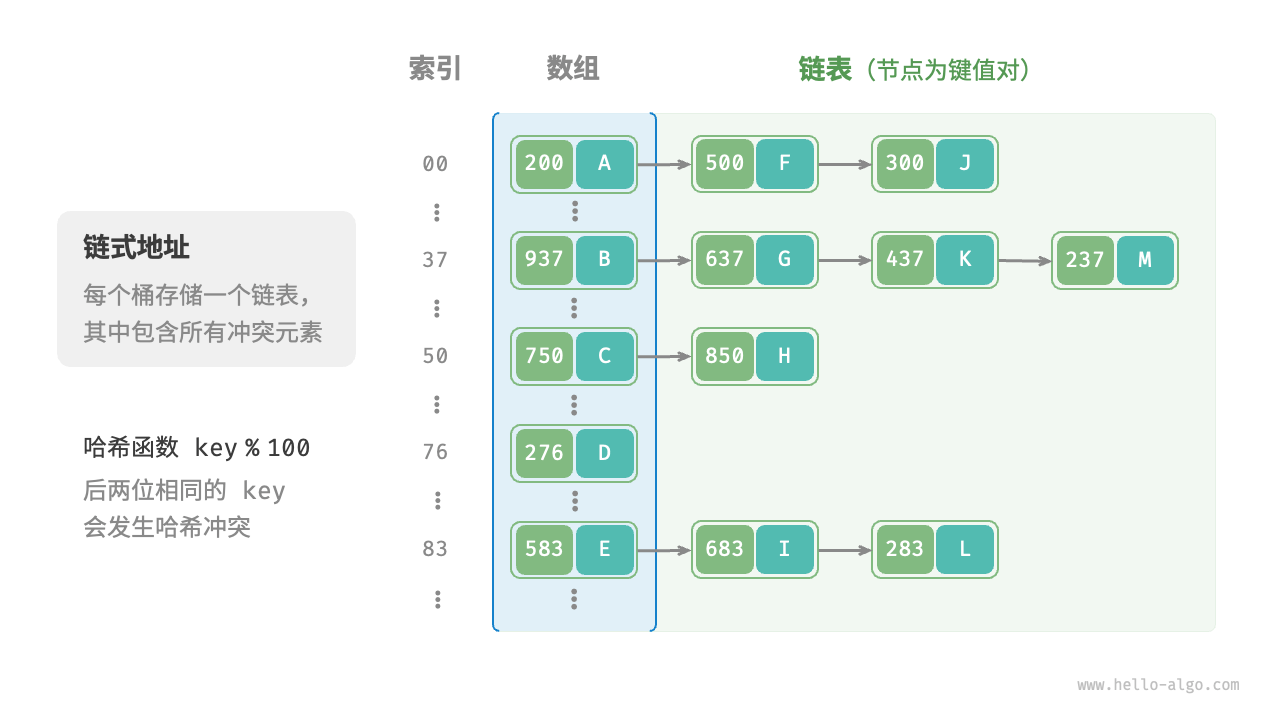
基于链式地址实现的哈希表的操作方法发生了以下变化。
- 查询元素:输入
key,经过哈希函数得到桶索引,即可访问链表头节点,然后遍历链表并对比key以查找目标键值对。 - 添加元素:首先通过哈希函数访问链表头节点,然后将节点(键值对)添加到链表中。
- 删除元素:根据哈希函数的结果访问链表头部,接着遍历链表以查找目标节点并将其删除。
链式地址存在以下局限性。
-
占用空间增大:链表包含节点指针,它相比数组更加耗费内存空间。
-
查询效率降低:因为需要线性遍历链表来查找对应元素。
-
使用列表(动态数组)代替链表,从而简化代码。在这种设定下,哈希表(数组)包含多个桶,每个桶都是一个列表。
-
以下实现包含哈希表扩容方法。当负载因子超过 $\frac{2}{3}$ 时,我们将哈希表扩容至原先的 2 倍
/* 链式地址哈希表 */
class HashMapChaining {
int size; // 键值对数量
int capacity; // 哈希表容量
double loadThres; // 触发扩容的负载因子阈值
int extendRatio; // 扩容倍数
List<List<Pair>> buckets; // 桶数组
/* 构造方法 */
public HashMapChaining() {
size = 0;
capacity = 4;
loadThres = 2.0 / 3.0;
extendRatio = 2;
buckets = new List<List<Pair>>(capacity);
for (int i = 0; i < capacity; i++) {
buckets.Add([]);
}
}
/* 哈希函数 */
int HashFunc(int key) {
return key % capacity;
}
/* 负载因子 */
double LoadFactor() {
return (double)size / capacity;
}
/* 查询操作 */
public string? Get(int key) {
int index = HashFunc(key);
// 遍历桶,若找到 key ,则返回对应 val
foreach (Pair pair in buckets[index]) {
if (pair.key == key) {
return pair.val;
}
}
// 若未找到 key ,则返回 null
return null;
}
/* 添加操作 */
public void Put(int key, string val) {
// 当负载因子超过阈值时,执行扩容
if (LoadFactor() > loadThres) {
Extend();
}
int index = HashFunc(key);
// 遍历桶,若遇到指定 key ,则更新对应 val 并返回
foreach (Pair pair in buckets[index]) {
if (pair.key == key) {
pair.val = val;
return;
}
}
// 若无该 key ,则将键值对添加至尾部
buckets[index].Add(new Pair(key, val));
size++;
}
/* 删除操作 */
public void Remove(int key) {
int index = HashFunc(key);
// 遍历桶,从中删除键值对
foreach (Pair pair in buckets[index].ToList()) {
if (pair.key == key) {
buckets[index].Remove(pair);
size--;
break;
}
}
}
/* 扩容哈希表 */
void Extend() {
// 暂存原哈希表
List<List<Pair>> bucketsTmp = buckets;
// 初始化扩容后的新哈希表
capacity *= extendRatio;
buckets = new List<List<Pair>>(capacity);
for (int i = 0; i < capacity; i++) {
buckets.Add([]);
}
size = 0;
// 将键值对从原哈希表搬运至新哈希表
foreach (List<Pair> bucket in bucketsTmp) {
foreach (Pair pair in bucket) {
Put(pair.key, pair.val);
}
}
}
/* 打印哈希表 */
public void Print() {
foreach (List<Pair> bucket in buckets) {
List<string> res = [];
foreach (Pair pair in bucket) {
res.Add(pair.key + " -> " + pair.val);
}
foreach (string kv in res) {
Console.WriteLine(kv);
}
}
}
}
当链表很长时,查询效率 O(n) 很差。**此时可以将链表转换为“AVL 树”或“红黑树”**,从而将查询操作的时间复杂度优化至 O(logn)
开放寻址
开放寻址(open addressing)不引入额外的数据结构,而是通过"多次探测"来处理哈希冲突
*线性探测
线性探测采用固定步长的线性搜索来进行探测,其操作方法与普通哈希表有所不同
- 插入元素:通过哈希函数计算桶索引,若发现桶内已有元素,则从冲突位置向后线性遍历(步长通常为 1 ),直至找到空桶,将元素插入其中。
- 查找元素:若发现哈希冲突,则使用相同步长向后进行线性遍历,直到找到对应元素,返回
value即可;如果遇到空桶,说明目标元素不在哈希表中,返回None
![]()
最后两位相同的key都会被映射到相同的桶。而通过线性探测,它们被依次存储在该桶以及之下的桶中
但线性探测容易产生聚集现象:数组中连续被占位置越长,这些连续位置发送哈希冲突的可能性越大,从而进一步促使该位置的聚堆生长,形成恶性循环,最终导致增删查改操作效率劣化
不能在开放寻址哈希表中直接删除元素,因为删除元素会在数组内产生一个空桶 None ,而当查询元素时,线性探测到该空桶就会返回,因此在该空桶之下的元素都无法再被访问到,程序可能误判这些元素不存在

为了解决该问题,可以采用懒删除(lazy deletion)机制:它不直接从哈希表中移除元素,而是利用一个常量 TOMBSTONE 来标记这个桶。在该机制下,None 和 TOMBSTONE 都代表空桶,都可以放置键值对。但不同的是,线性探测到 TOMBSTONE 时应该继续遍历,因为其之下可能还存在键值对。
但懒删除可能会加速哈希表的性能退化。这是因为每次删除操作都会产生一个删除标记,随着 TOMBSTONE 的增加,搜索时间也会增加,因为线性探测可能需要跳过多个 TOMBSTONE 才能找到目标元素。
为此,考虑在线性探测中记录遇到的首个 TOMBSTONE 的索引,并将搜索到的目标元素与该 TOMBSTONE 交换位置。这样做的好处是当每次查询或添加元素时,元素会被移动至距离理想位置(探测起始点)更近的桶,从而优化查询效率。
以下代码实现了一个包含懒删除的开放寻址(线性探测)哈希表。为了更加充分地使用哈希表的空间,我们将哈希表看作一个“环形数组”,当越过数组尾部时,回到头部继续遍历
/* 开放寻址哈希表 */
class HashMapOpenAddressing {
int size; // 键值对数量
int capacity = 4; // 哈希表容量
double loadThres = 2.0 / 3.0; // 触发扩容的负载因子阈值
int extendRatio = 2; // 扩容倍数
Pair[] buckets; // 桶数组
Pair TOMBSTONE = new(-1, "-1"); // 删除标记
/* 构造方法 */
public HashMapOpenAddressing() {
size = 0;
buckets = new Pair[capacity];
}
/* 哈希函数 */
int HashFunc(int key) {
return key % capacity;
}
/* 负载因子 */
double LoadFactor() {
return (double)size / capacity;
}
/* 搜索 key 对应的桶索引 */
int FindBucket(int key) {
int index = HashFunc(key);
int firstTombstone = -1;
// 线性探测,当遇到空桶时跳出
while (buckets[index] != null) {
// 若遇到 key ,返回对应的桶索引
if (buckets[index].key == key) {
// 若之前遇到了删除标记,则将键值对移动至该索引处
if (firstTombstone != -1) {
buckets[firstTombstone] = buckets[index];
buckets[index] = TOMBSTONE;
return firstTombstone; // 返回移动后的桶索引
}
return index; // 返回桶索引
}
// 记录遇到的首个删除标记
if (firstTombstone == -1 && buckets[index] == TOMBSTONE) {
firstTombstone = index;
}
// 计算桶索引,越过尾部则返回头部
index = (index + 1) % capacity;
}
// 若 key 不存在,则返回添加点的索引
return firstTombstone == -1 ? index : firstTombstone;
}
/* 查询操作 */
public string? Get(int key) {
// 搜索 key 对应的桶索引
int index = FindBucket(key);
// 若找到键值对,则返回对应 val
if (buckets[index] != null && buckets[index] != TOMBSTONE) {
return buckets[index].val;
}
// 若键值对不存在,则返回 null
return null;
}
/* 添加操作 */
public void Put(int key, string val) {
// 当负载因子超过阈值时,执行扩容
if (LoadFactor() > loadThres) {
Extend();
}
// 搜索 key 对应的桶索引
int index = FindBucket(key);
// 若找到键值对,则覆盖 val 并返回
if (buckets[index] != null && buckets[index] != TOMBSTONE) {
buckets[index].val = val;
return;
}
// 若键值对不存在,则添加该键值对
buckets[index] = new Pair(key, val);
size++;
}
/* 删除操作 */
public void Remove(int key) {
// 搜索 key 对应的桶索引
int index = FindBucket(key);
// 若找到键值对,则用删除标记覆盖它
if (buckets[index] != null && buckets[index] != TOMBSTONE) {
buckets[index] = TOMBSTONE;
size--;
}
}
/* 扩容哈希表 */
void Extend() {
// 暂存原哈希表
Pair[] bucketsTmp = buckets;
// 初始化扩容后的新哈希表
capacity *= extendRatio;
buckets = new Pair[capacity];
size = 0;
// 将键值对从原哈希表搬运至新哈希表
foreach (Pair pair in bucketsTmp) {
if (pair != null && pair != TOMBSTONE) {
Put(pair.key, pair.val);
}
}
}
/* 打印哈希表 */
public void Print() {
foreach (Pair pair in buckets) {
if (pair == null) {
Console.WriteLine("null");
} else if (pair == TOMBSTONE) {
Console.WriteLine("TOMBSTONE");
} else {
Console.WriteLine(pair.key + " -> " + pair.val);
}
}
}
}
*平方探测
平方探测不是简单跳过一个固定步数,而是跳过"探测次数的平方"的步数,即1,4,9,...步
- 平方探测通过跳过探测次数平方的距离,试图缓解线性探测的聚集效应。
- 平方探测会跳过更大的距离来寻找空位置,有助于数据分布得更加均匀。
然而,平方探测并不是完美的。
- 仍然存在聚集现象,即某些位置比其他位置更容易被占用。
- 由于平方的增长,平方探测可能不会探测整个哈希表,这意味着即使哈希表中有空桶,平方探测也可能无法访问到它
*多次哈希
多次哈希即使用多个哈希函数进行探测
- 插入元素:若哈希函数 f1(x) 出现冲突,则尝试 f2(x) ,以此类推,直到找到空位后插入元素
- 查找元素:在相同的哈希函数顺序下进行查找,直到找到目标元素时返回;若遇到空位或已尝试所有哈希函数,说明哈希表中不存在该元素,则返回
None
与线性探测相比,多次哈希方法不易产生聚集,但多个哈希函数会带来额外的计算量
***开放寻址(线性探测、平方探测和多次哈希)哈希表都存在“不能直接删除元素”的问题***
哈希算法
链式地址和开放寻址只能保证在发生冲突时哈希表正常工作,无法减少哈希冲突的发生
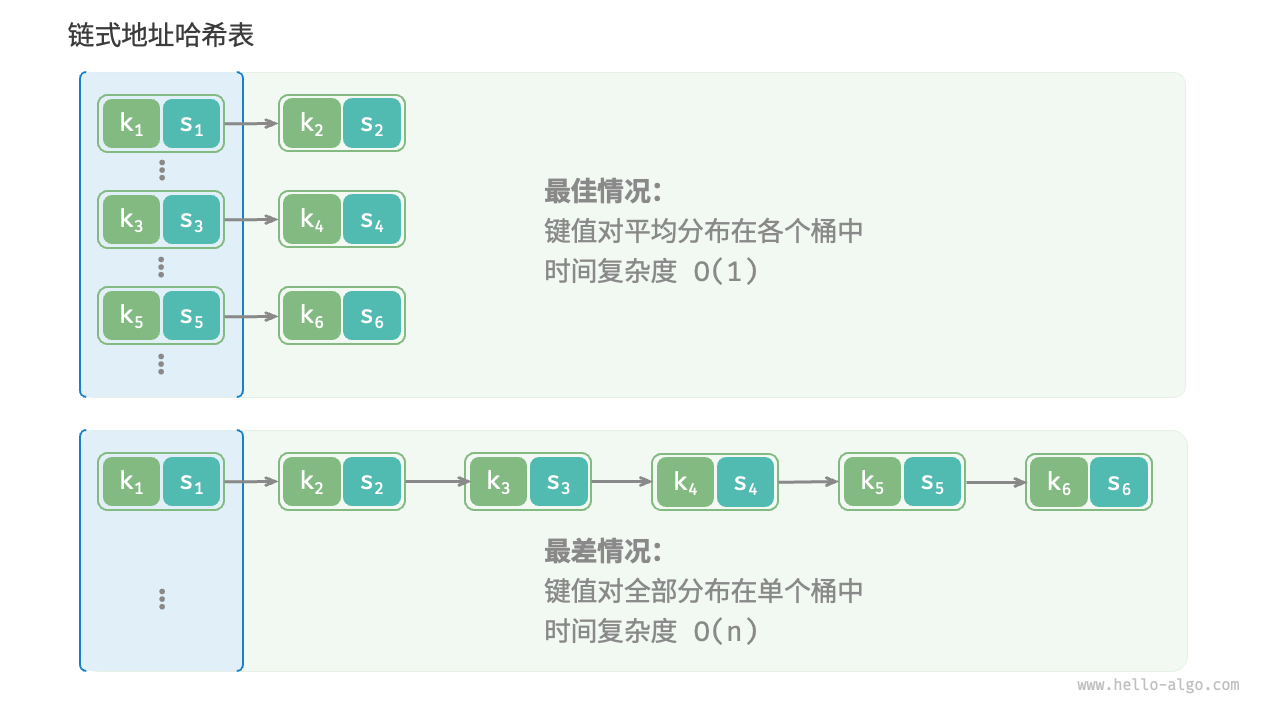
哈希算法应具备以下特点:
- 确定性:对于相同的输入,哈希算法应始终产生相同的输出。这样才能确保哈希表是可靠的。
- 效率高:计算哈希值的过程应该足够快。计算开销越小,哈希表的实用性越高。
- 均匀分布:哈希算法应使得键值对均匀分布在哈希表中。分布越均匀,哈希冲突的概率就越低。
哈希算法除了可以用于实现哈希表,还广泛应用于其他领域中:
- 密码存储:为了保护用户密码的安全,系统通常不会直接存储用户的明文密码,而是存储密码的哈希值。当用户输入密码时,系统会对输入的密码计算哈希值,然后与存储的哈希值进行比较。如果两者匹配,那么密码就被视为正确。
- 数据完整性检查:数据发送方可以计算数据的哈希值并将其一同发送;接收方可以重新计算接收到的数据的哈希值,并与接收到的哈希值进行比较。如果两者匹配,那么数据就被视为完整。
对于密码学的相关应用,为了防止从哈希值推导出原始密码等逆向工程,哈希算法需要具备更高等级的安全特性:
- 单向性:无法通过哈希值反推出关于输入数据的任何信息。
- 抗碰撞性:应当极难找到两个不同的输入,使得它们的哈希值相同。
- 雪崩效应:输入的微小变化应当导致输出的显著且不可预测的变化
简单的哈希算法
- 加法哈希:对输入的每个字符的 ASCII 码进行相加,将得到的总和作为哈希值。
- 乘法哈希:利用乘法的不相关性,每轮乘以一个常数,将各个字符的 ASCII 码累积到哈希值中。
- 异或哈希:将输入数据的每个元素通过异或操作累积到一个哈希值中。
- 旋转哈希:将每个字符的 ASCII 码累积到一个哈希值中,每次累积之前都会对哈希值进行旋转操作
/* 加法哈希 */
int AddHash(string key) {
long hash = 0;
const int MODULUS = 1000000007;
foreach (char c in key) {
hash = (hash + c) % MODULUS;
}
return (int)hash;
}
/* 乘法哈希 */
int MulHash(string key) {
long hash = 0;
const int MODULUS = 1000000007;
foreach (char c in key) {
hash = (31 * hash + c) % MODULUS;
}
return (int)hash;
}
/* 异或哈希 */
int XorHash(string key) {
int hash = 0;
const int MODULUS = 1000000007;
foreach (char c in key) {
hash ^= c;
}
return hash & MODULUS;
}
/* 旋转哈希 */
int RotHash(string key) {
long hash = 0;
const int MODULUS = 1000000007;
foreach (char c in key) {
hash = ((hash << 4) ^ (hash >> 28) ^ c) % MODULUS;
}
return (int)hash;
}
使用大质数作为模数,可以最大化地保证哈希值的均匀分布。因为质数不与其他数字存在公约数,可以减少因取模操作而产生的周期性模式,从而避免哈希冲突
| MD5 | SHA-1 | SHA-2 | SHA-3 | |
|---|---|---|---|---|
| 推出时间 | 1992 | 1995 | 2002 | 2008 |
| 输出长度 | 128 bit | 160 bit | 256/512 bit | 224/256/384/512 bit |
| 哈希冲突 | 较多 | 较多 | 很少 | 很少 |
| 安全等级 | 低,已被成功攻击 | 低,已被成功攻击 | 高 | 高 |
| 应用 | 已被弃用,仍用于数据完整性检查 | 已被弃用 | 加密货币交易验证、数字签名等 | 可用于替代 SHA-2 |
树
二叉树
二叉树(binary tree)是一种非线性数据结构,代表"祖先"与"后代"之间的派生关系,体现一份为二的分治逻辑.与链表类似,二叉树基本单元是节点,每个节点包含值,左子节点引用和右子节点引用
/* 二叉树节点类 */
class TreeNode(int? x) {
public int? val = x; // 节点值
public TreeNode? left; // 左子节点引用
public TreeNode? right; // 右子节点引用
}
当给定一个二叉树的节点时,将该节点的左子节点及其以下节点形成的树称为该节点的左子树,同理可得右子树
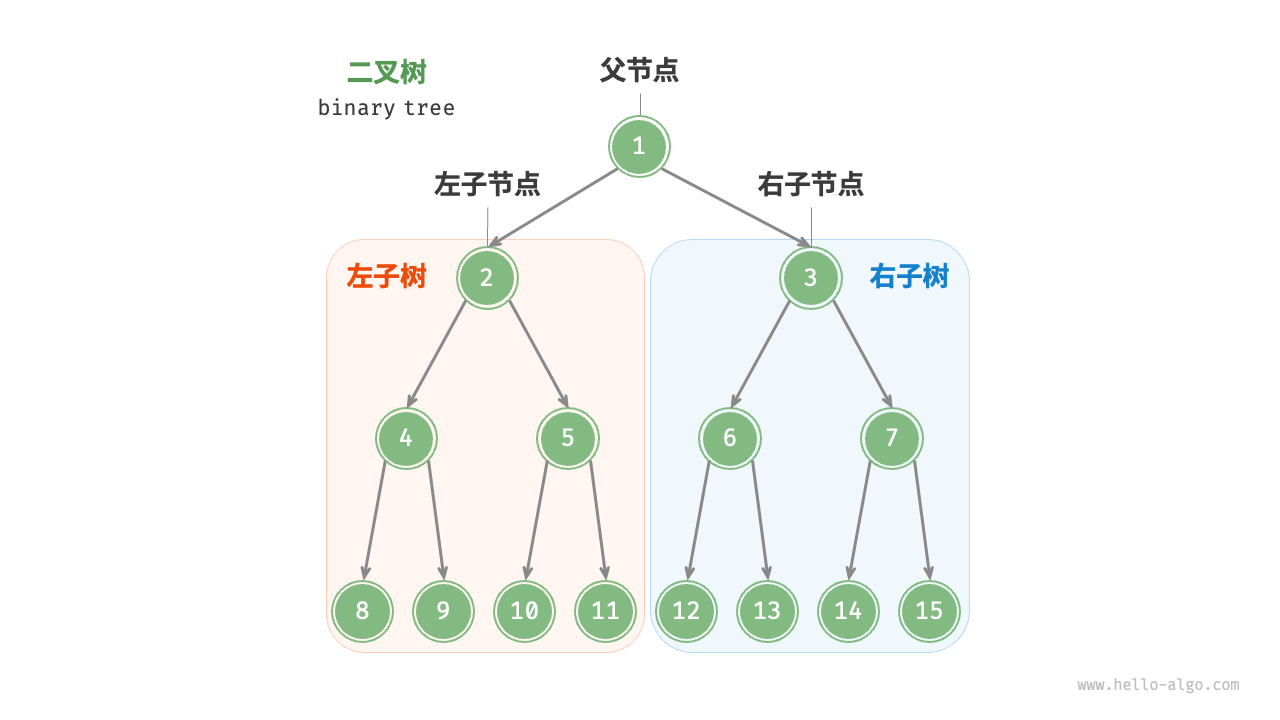
*二叉树常用术语
- 根节点:位于二叉树顶层的节点,没有父节点
- 叶节点:没有子节点的节点,其两个指针均指向
None - 边:连接两个节点的线段,即节点引用(指针)
- 节点所在的层:从顶至底递增,根节点所在层为 1
- 节点的度:节点的子节点的数量。在二叉树中,度的取值范围是 0、1、2
- 二叉树的高度:从根节点到最远叶节点所经过的边的数量
- 节点的深度:从根节点到该节点所经过的边的数量
- 节点的高度:从距离该节点最远的叶节点到该节点所经过的边的数量
![]()
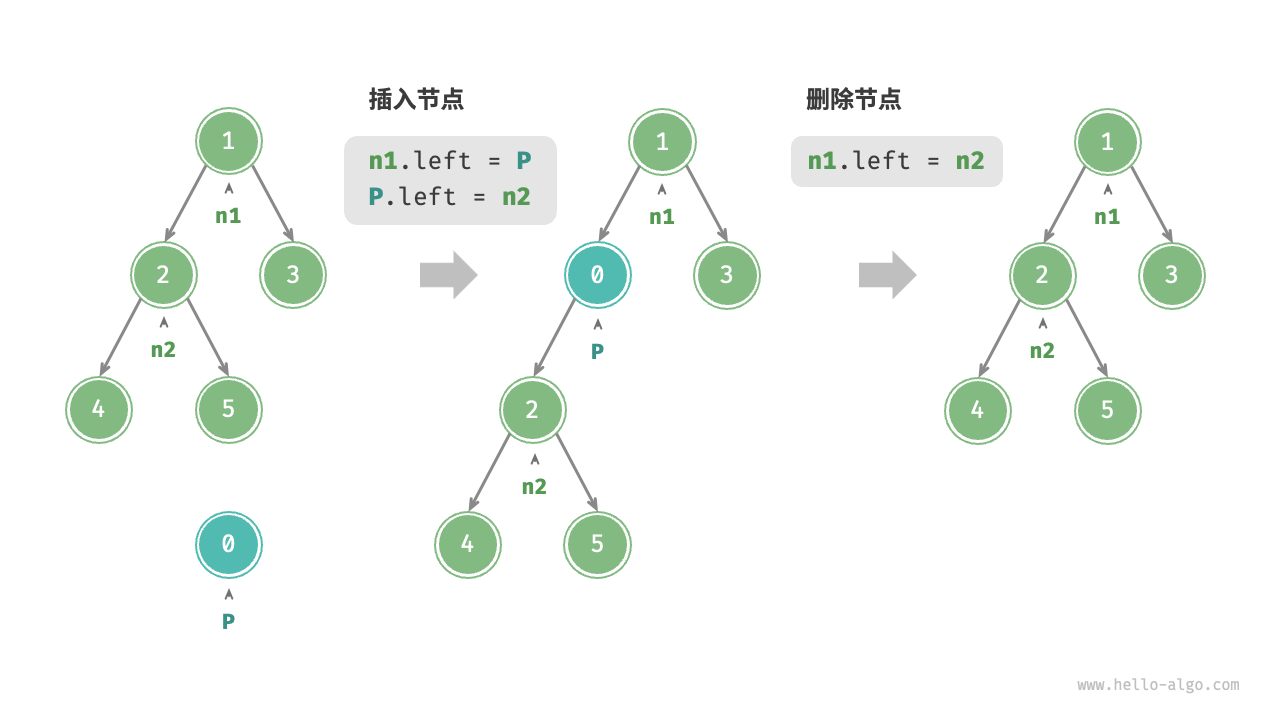
*二叉树基本操作
/* 初始化二叉树 */
// 初始化节点
TreeNode n1 = new(1);
TreeNode n2 = new(2);
TreeNode n3 = new(3);
TreeNode n4 = new(4);
TreeNode n5 = new(5);
// 构建节点之间的引用(指针)
n1.left = n2;
n1.right = n3;
n2.left = n4;
n2.right = n5;
/* 插入与删除节点 */
TreeNode P = new(0);
// 在 n1 -> n2 中间插入节点 P
n1.left = P;
P.left = n2;
// 删除节点 P
n1.left = n2;
*常见二叉树类型
-
完美二叉树(满二叉树)
![]()
叶节点的度为 0 ,其余所有节点的度都为 2 ;若树的高度为 h ,则节点总数为 $2^{h+1}−1$ ,呈现标准的指数级关系 -
完全二叉树
![]()
只有最底层的节点未被填满,且最底层节点尽量靠左填充。请注意,完美二叉树也是一棵完全二叉树 -
完满二叉树
![]()
除叶节点之外,其余节点都有两个子节点 -
平衡二叉树
![]()
任意节点的左子树和右子树高度之差的绝对值不超过1
二叉树的退化:
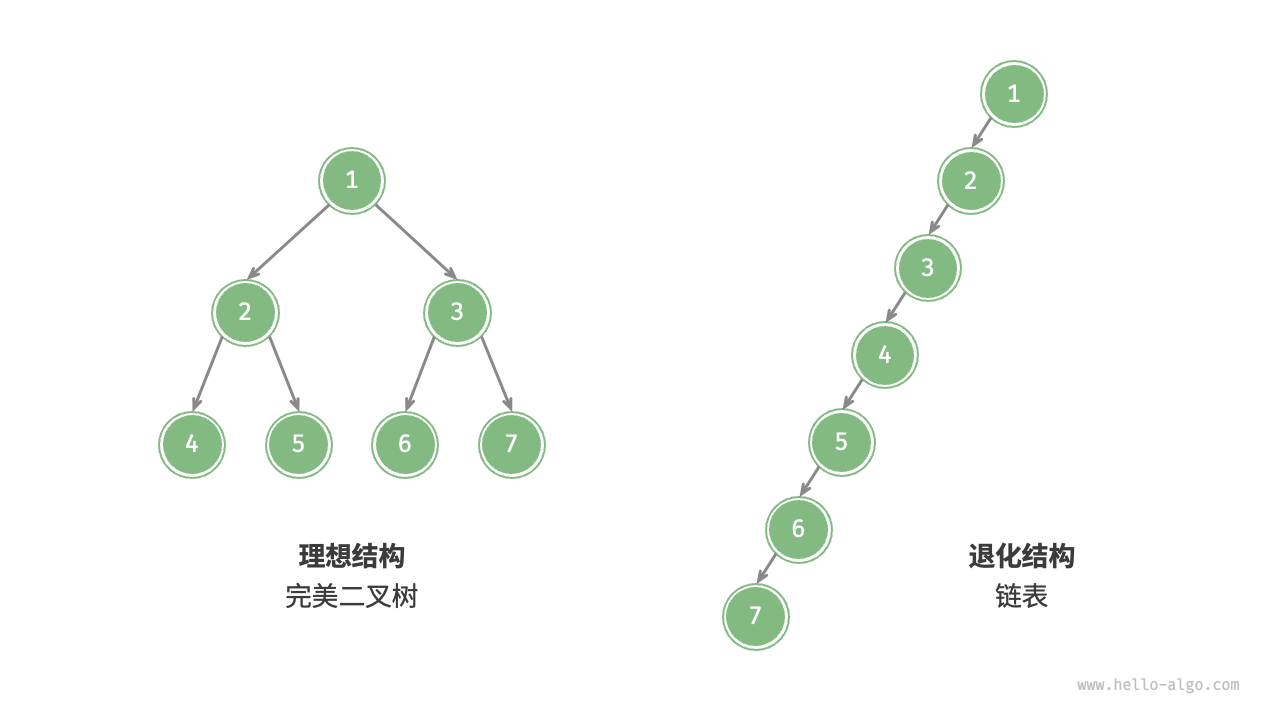
二叉树遍历
***层序遍历
从顶部到底部逐层遍历二叉树,并在每一层按照从左到右的顺序访问节点
层序遍历本质上属于广度优先遍历,也称广度优先搜索,体现一种"一圈一圈向外扩展"的逐层遍历方式
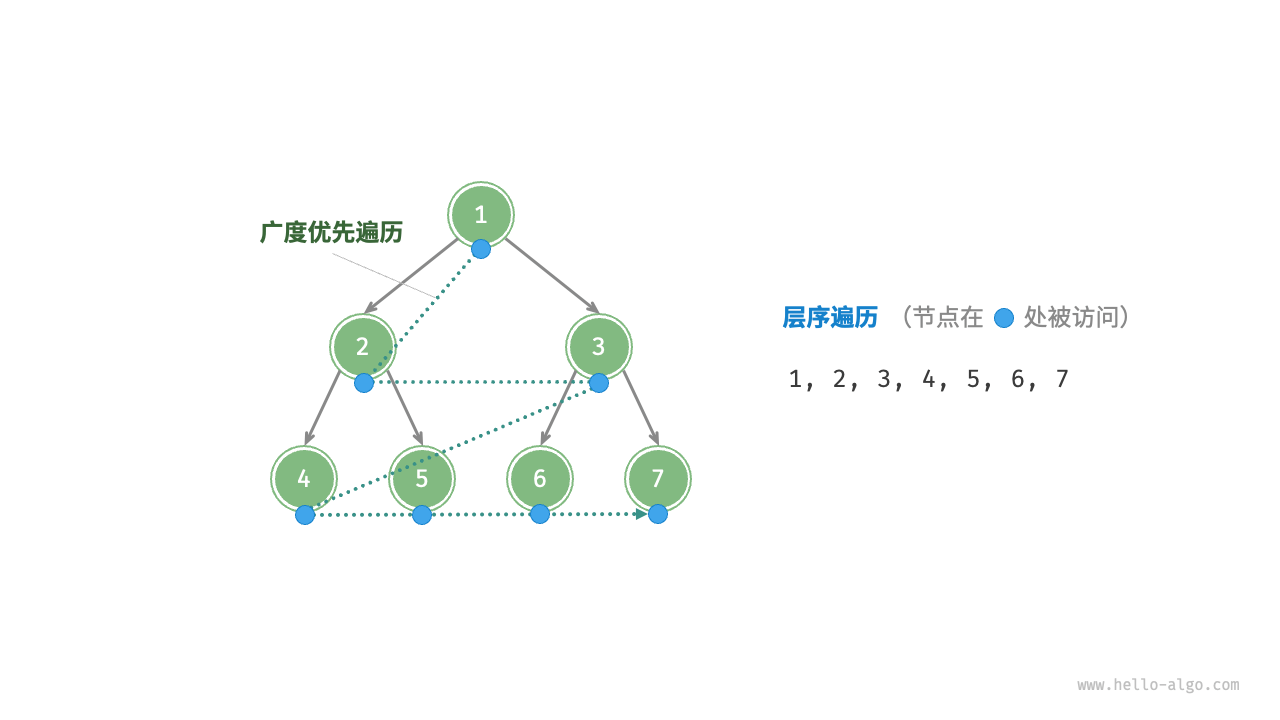
/* 层序遍历 */
List<int> LevelOrder(TreeNode root) {
// 初始化队列,加入根节点
Queue<TreeNode> queue = new();
queue.Enqueue(root);
// 初始化一个列表,用于保存遍历序列
List<int> list = [];
while (queue.Count != 0) {
TreeNode node = queue.Dequeue(); // 队列出队
list.Add(node.val!.Value); // 保存节点值
if (node.left != null)
queue.Enqueue(node.left); // 左子节点入队
if (node.right != null)
queue.Enqueue(node.right); // 右子节点入队
}
return list;
}
***前序,中序,后序遍历
都属于深度优先遍历,也称深度优先搜索,体现一种"先走到尽头,再回溯继续"的遍历方式
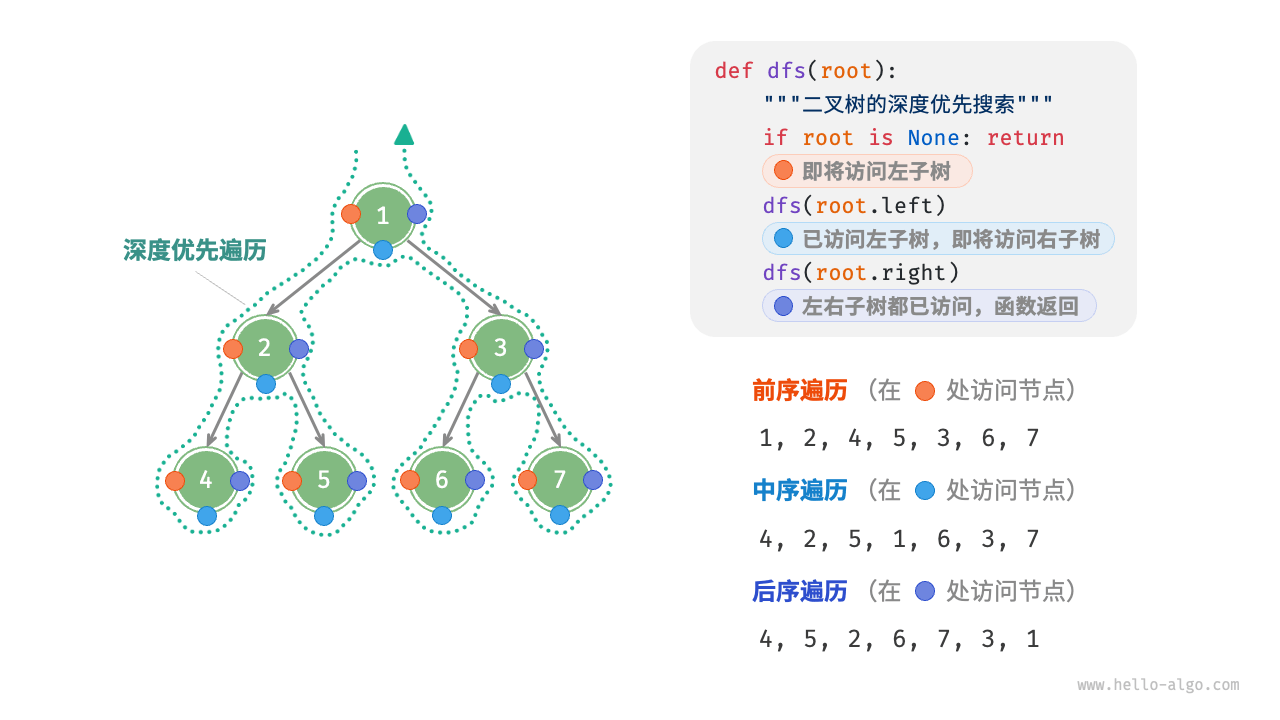
/* 前序遍历*/
void PreOrder(TreeNode? root) {
if (root == null) return;
// 访问优先级:根节点 -> 左子树 -> 右子树
list.Add(root.val!.Value);
PreOrder(root.left);
PreOrder(root.right);
}
void PreOrderNonRecursive(TreeNode root) {
if (root == null) return;
Stack<TreeNode> stack = new Stack<TreeNode>();
List<int> list = new List<int>();
stack.Push(root);
while (stack.Count > 0) {
TreeNode node = stack.Pop();
list.Add(node.val.Value); // 访问根节点
// 先右后左入栈,保证左子树先被访问
if (node.right != null) {
stack.Push(node.right);
}
if (node.left != null) {
stack.Push(node.left);
}
}
}
/* 中序遍历 */
void InOrder(TreeNode? root) {
if (root == null) return;
// 访问优先级:左子树 -> 根节点 -> 右子树
InOrder(root.left);
list.Add(root.val!.Value);
InOrder(root.right);
}
void InOrderNonRecursive(TreeNode root) {
if (root == null) return;
Stack<TreeNode> stack = new Stack<TreeNode>();
List<int> list = new List<int>();
TreeNode current = root;
while (current != null || stack.Count > 0) {
// 先遍历到最左端的节点
while (current != null) {
stack.Push(current);
current = current.left;
}
// 访问栈顶元素,即当前节点
current = stack.Pop();
list.Add(current.val.Value); // 访问根节点
// 转向右子节点
current = current.right;
}
}
/* 后序遍历 */
void PostOrder(TreeNode? root) {
if (root == null) return;
// 访问优先级:左子树 -> 右子树 -> 根节点
PostOrder(root.left);
PostOrder(root.right);
list.Add(root.val!.Value);
}
void PostOrderNonRecursive(TreeNode root) {
if (root == null) return;
Stack<TreeNode> stack1 = new Stack<TreeNode>();
Stack<TreeNode> stack2 = new Stack<TreeNode>();
List<int> list = new List<int>();
stack1.Push(root);
while (stack1.Count > 0) {
TreeNode node = stack1.Pop();
stack2.Push(node);
// 先左后右入栈
if (node.left != null) {
stack1.Push(node.left);
}
if (node.right != null) {
stack1.Push(node.right);
}
}
// 从stack2中依次弹出元素,即为后序遍历结果
while (stack2.Count > 0) {
TreeNode node = stack2.Pop();
list.Add(node.val.Value);
}
}
二叉树数组表示
根据层序遍历的特性,我们可以推导出父节点索引与子节点索引之间的“映射公式”:若某节点的索引为 i ,则该节点的左子节点索引为 2i+1 ,右子节点索引为2i+2
映射公式的角色相当于链表中的节点引用,给定数组任意一个节点,都可以通过映射公式来访问左右节点
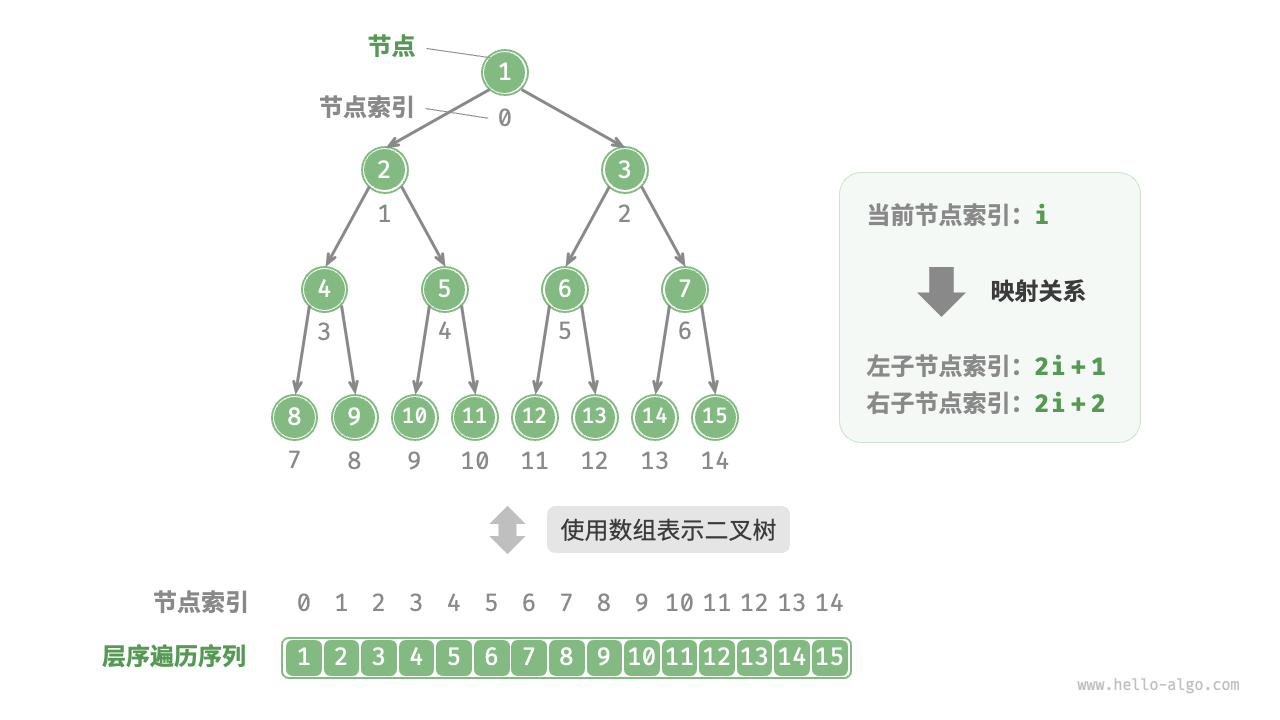
但给定一个非完美二叉树,上述数组表示方法已经失效
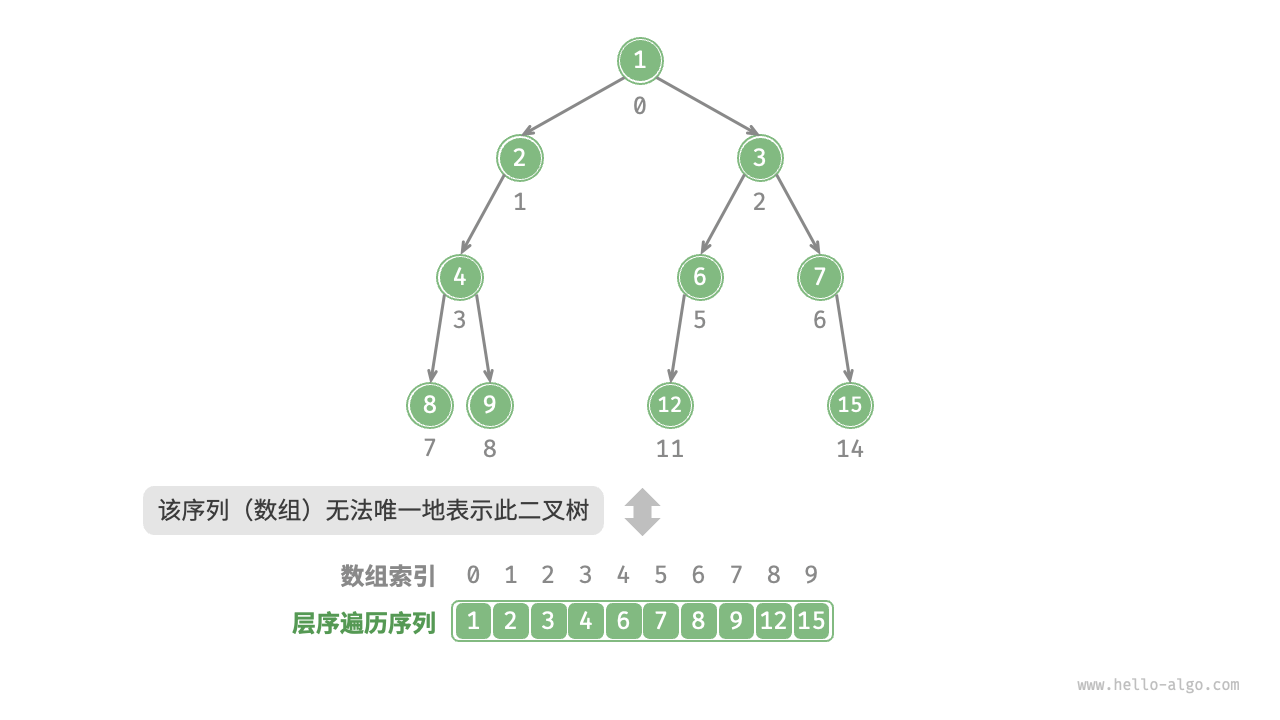
为了解决此问题,可以考虑在层序遍历序列中显示写出所有空
/* 二叉树的数组表示 */
// 使用 int? 可空类型 ,就可以使用 null 来标记空位
int?[] tree = [1, 2, 3, 4, null, 6, 7, 8, 9, null, null, 12, null, null, 15];
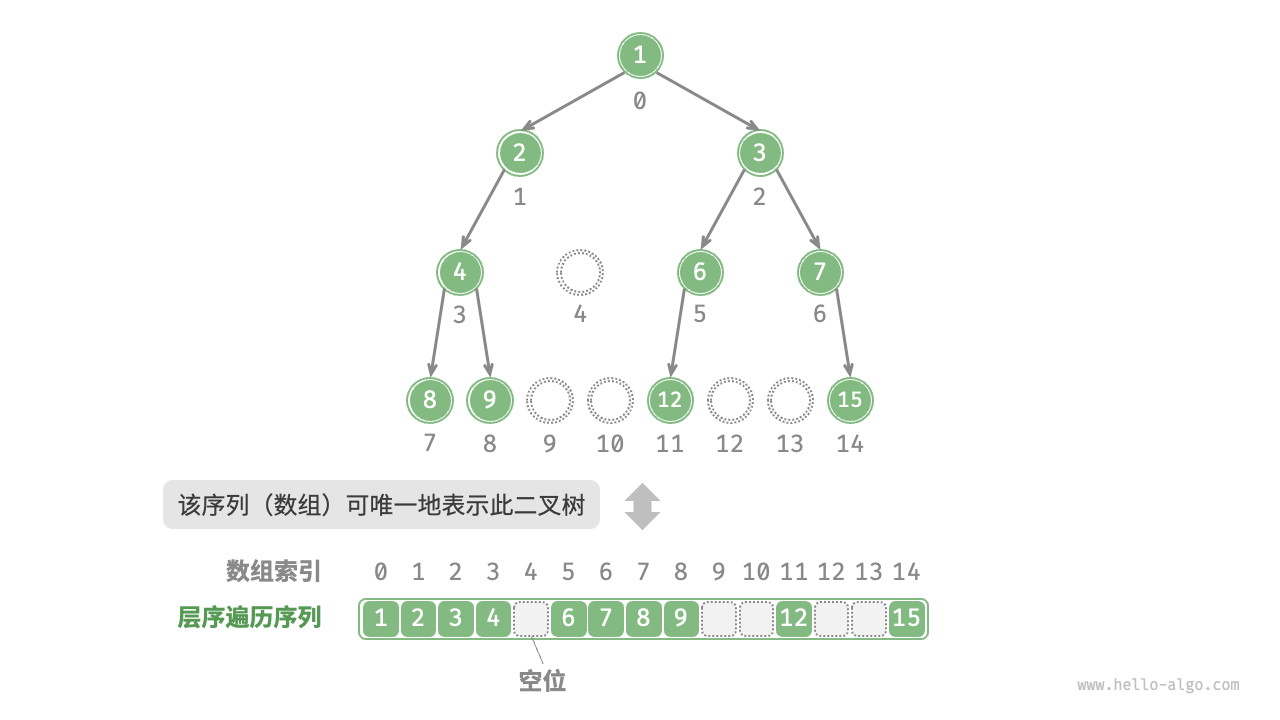
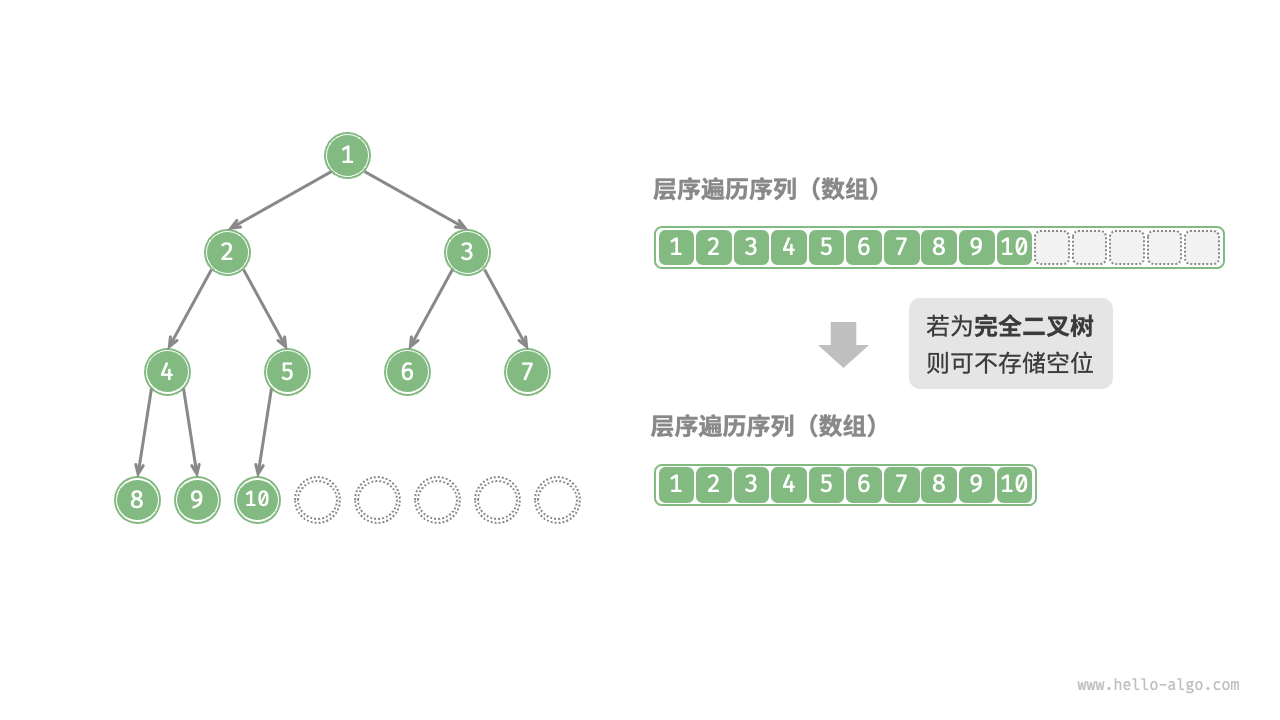
完全二叉树非常适合使用数组来表示。回顾完全二叉树的定义,None只出现在最底层且靠右的位置,因此所有 None 一定出现在层序遍历序列的末尾
/* 数组表示下的二叉树类 */
class ArrayBinaryTree(List<int?> arr) {
List<int?> tree = new(arr);
/* 列表容量 */
public int Size() {
return tree.Count;
}
/* 获取索引为 i 节点的值 */
public int? Val(int i) {
// 若索引越界,则返回 null ,代表空位
if (i < 0 || i >= Size())
return null;
return tree[i];
}
/* 获取索引为 i 节点的左子节点的索引 */
public int Left(int i) {
return 2 * i + 1;
}
/* 获取索引为 i 节点的右子节点的索引 */
public int Right(int i) {
return 2 * i + 2;
}
/* 获取索引为 i 节点的父节点的索引 */
public int Parent(int i) {
return (i - 1) / 2;
}
/* 层序遍历 */
public List<int> LevelOrder() {
List<int> res = [];
// 直接遍历数组
for (int i = 0; i < Size(); i++) {
if (Val(i).HasValue)
res.Add(Val(i)!.Value);
}
return res;
}
/* 深度优先遍历 */
void DFS(int i, string order, List<int> res) {
// 若为空位,则返回
if (!Val(i).HasValue)
return;
// 前序遍历
if (order == "pre")
res.Add(Val(i)!.Value);
DFS(Left(i), order, res);
// 中序遍历
if (order == "in")
res.Add(Val(i)!.Value);
DFS(Right(i), order, res);
// 后序遍历
if (order == "post")
res.Add(Val(i)!.Value);
}
/* 前序遍历 */
public List<int> PreOrder() {
List<int> res = [];
DFS(0, "pre", res);
return res;
}
/* 中序遍历 */
public List<int> InOrder() {
List<int> res = [];
DFS(0, "in", res);
return res;
}
/* 后序遍历 */
public List<int> PostOrder() {
List<int> res = [];
DFS(0, "post", res);
return res;
}
}
二叉树的数组表示主要有以下优点:
- 数组存储在连续的内存空间中,对缓存友好,访问与遍历速度较快
- 不需要存储指针,比较节省空间
- 允许随机访问节点
数组表示也存在一些局限性:
- 数组存储需要连续内存空间,因此不适合存储数据量过大的树
- 增删节点需要通过数组插入与删除操作实现,效率较低
- 当二叉树中存在大量
None时,数组中包含的节点数据比重较低,空间利用率较低
二叉搜索树
二叉搜索树(binary search tree)满足以下条件:
- 对于根节点,左子树中所有节点的值 < 根节点的值 < 右子树中所有节点的值。
- 任意节点的左、右子树也是二叉搜索树,即同样满足条件
1.
![]()
插入节点
给定一个待插入元素 num
- 查找插入位置:与查找操作相似,从根节点出发,根据当前节点值和
num的大小关系循环向下搜索,直到越过叶节点(遍历至None)时跳出循环。 - 在该位置插入节点:初始化节点
num,将该节点置于None的位置
![]()
- 二叉搜索树不允许存在重复节点,否则将违反其定义。因此,若待插入节点在树中已存在,则不执行插入,直接返回。
- 为了实现插入节点,我们需要借助节点
pre保存上一轮循环的节点。这样在遍历至None时,我们可以获取到其父节点,从而完成节点插入操作
/* 插入节点 */
void Insert(int num) {
// 若树为空,则初始化根节点
if (root == null) {
root = new TreeNode(num);
return;
}
TreeNode? cur = root, pre = null;
// 循环查找,越过叶节点后跳出
while (cur != null) {
// 找到重复节点,直接返回
if (cur.val == num)
return;
pre = cur;
// 插入位置在 cur 的右子树中
if (cur.val < num)
cur = cur.right;
// 插入位置在 cur 的左子树中
else
cur = cur.left;
}
// 插入节点
TreeNode node = new(num);
if (pre != null) {
if (pre.val < num)
pre.right = node;
else
pre.left = node;
}
}
删除节点
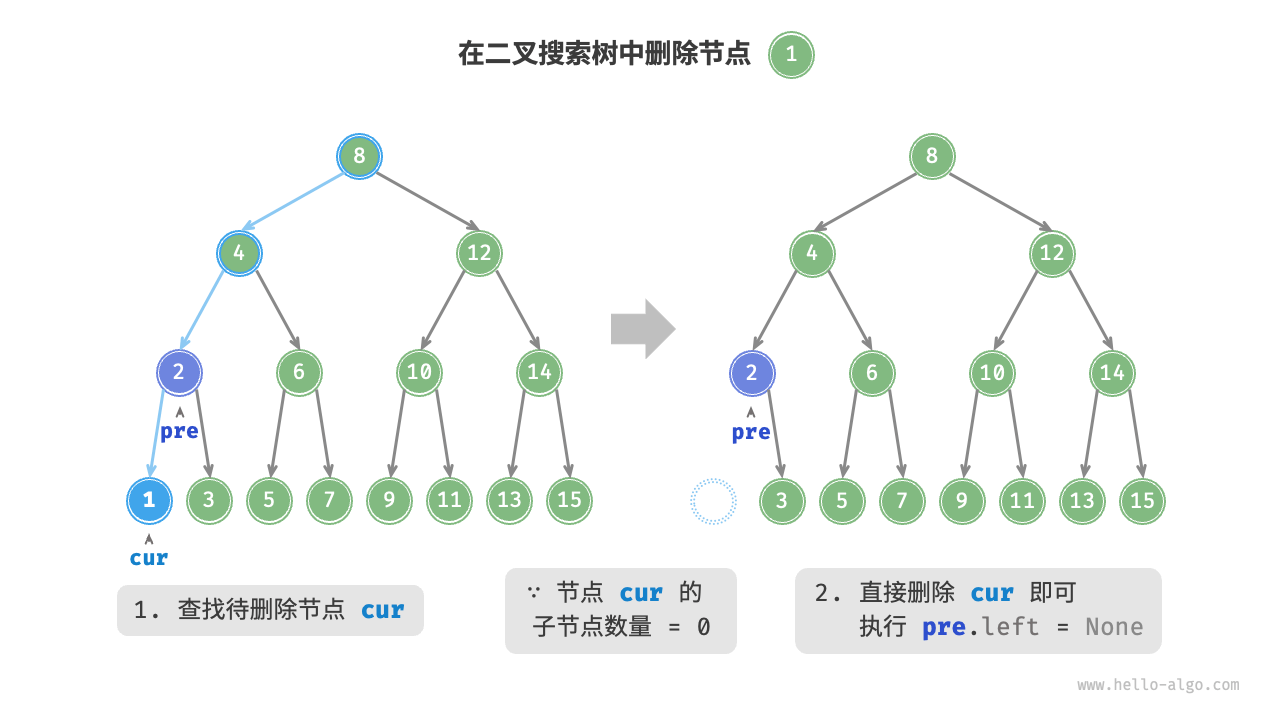
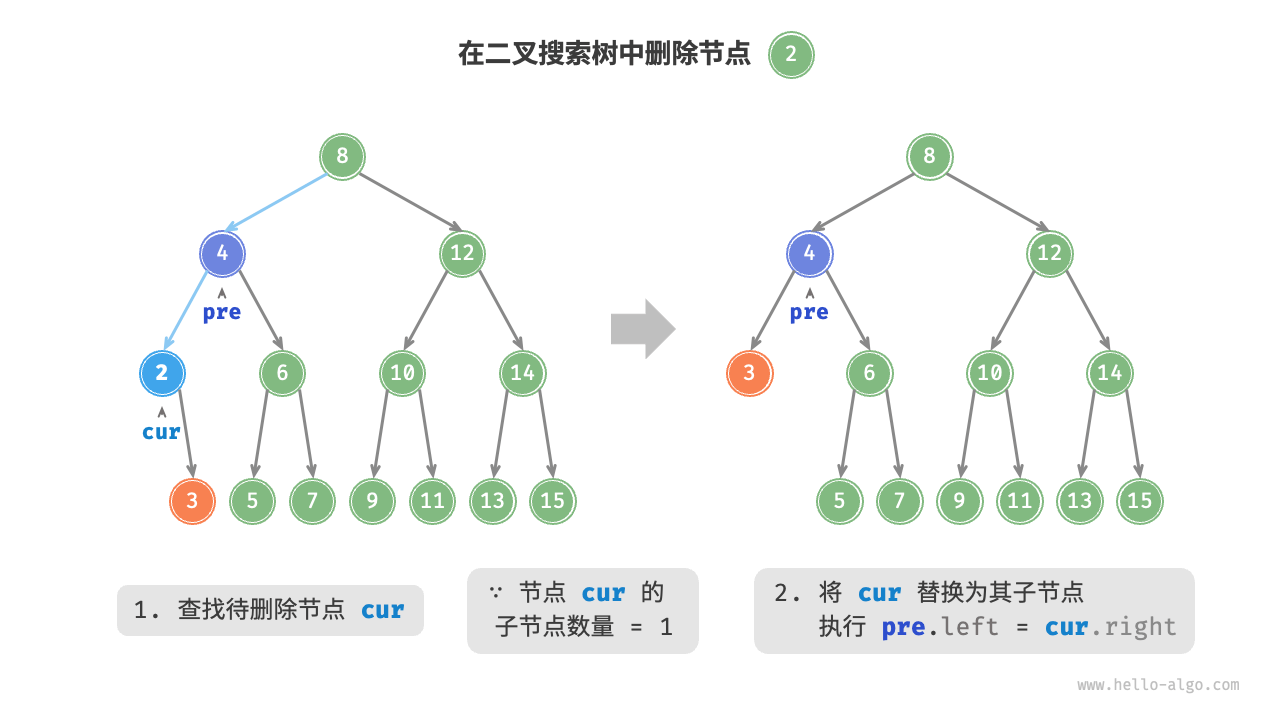
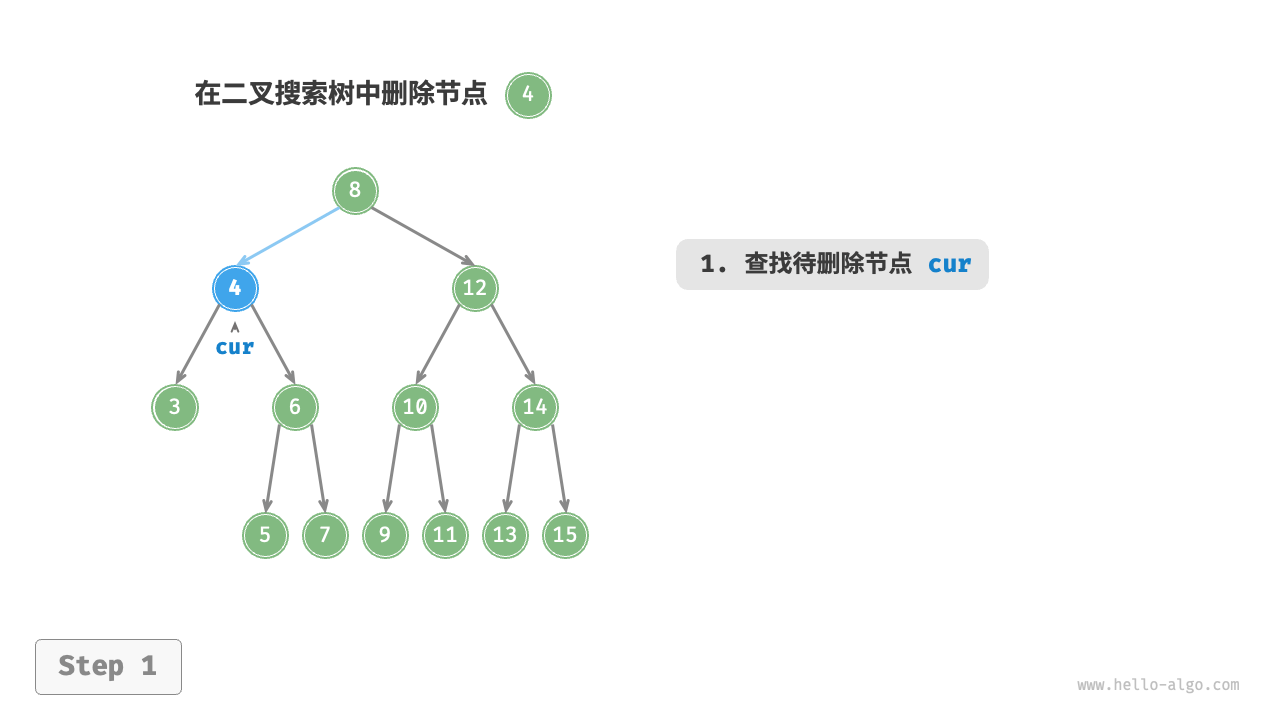
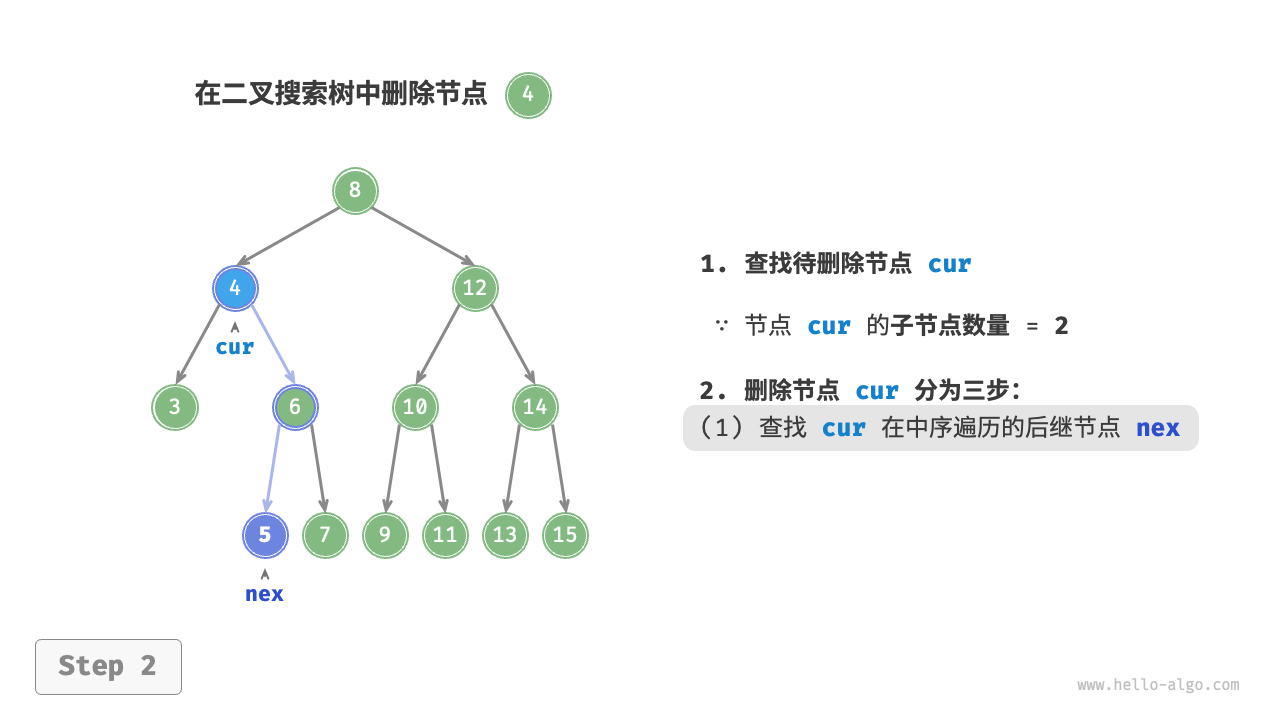
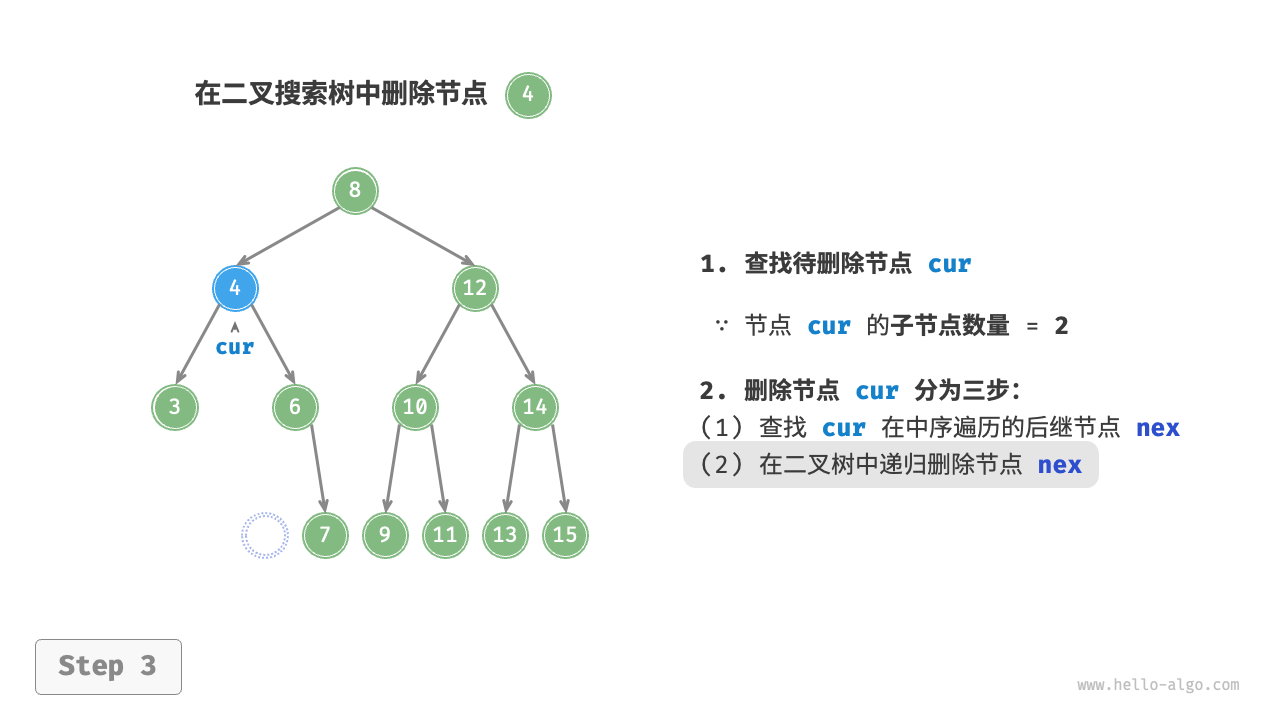
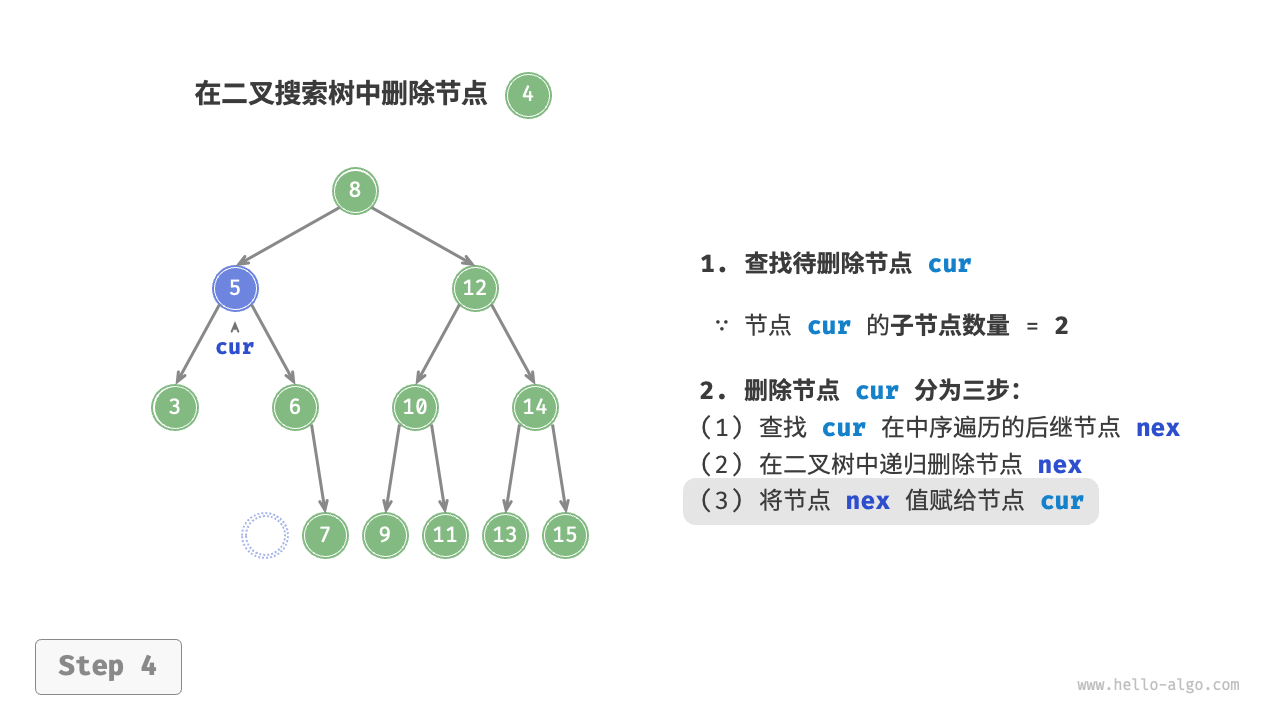
/* 删除节点 */
void Remove(int num) {
// 若树为空,直接提前返回
if (root == null)
return;
TreeNode? cur = root, pre = null;
// 循环查找,越过叶节点后跳出
while (cur != null) {
// 找到待删除节点,跳出循环
if (cur.val == num)
break;
pre = cur;
// 待删除节点在 cur 的右子树中
if (cur.val < num)
cur = cur.right;
// 待删除节点在 cur 的左子树中
else
cur = cur.left;
}
// 若无待删除节点,则直接返回
if (cur == null)
return;
// 子节点数量 = 0 or 1
if (cur.left == null || cur.right == null) {
// 当子节点数量 = 0 / 1 时, child = null / 该子节点
TreeNode? child = cur.left ?? cur.right;
// 删除节点 cur
if (cur != root) {
if (pre!.left == cur)
pre.left = child;
else
pre.right = child;
} else {
// 若删除节点为根节点,则重新指定根节点
root = child;
}
}
// 子节点数量 = 2
else {
// 获取中序遍历中 cur 的下一个节点
TreeNode? tmp = cur.right;
while (tmp.left != null) {
tmp = tmp.left;
}
// 递归删除节点 tmp
Remove(tmp.val!.Value);
// 用 tmp 覆盖 cur
cur.val = tmp.val;
}
}
*二叉搜索树常见应用
- 用作系统中的多级索引,实现高效的查找、插入、删除操作。
- 作为某些搜索算法的底层数据结构。
- 用于存储数据流,以保持其有序状态。
AVL树
AVL树既是二叉搜索树,也是平衡二叉树,同时满足这两类二叉树的所有性质,因此是一种平衡二叉搜索树
由于 AVL 树的相关操作需要获取节点高度,因此需要为节点类添加 height 变量:
/* AVL 树节点类 */
class TreeNode(int? x) {
public int? val = x; // 节点值
public int height; // 节点高度
public TreeNode? left; // 左子节点引用
public TreeNode? right; // 右子节点引用
}
节点高度”是指从该节点到它的最远叶节点的距离,即所经过的“边”的数量。需要特别注意的是,叶节点的高度为 0 ,而空节点的高度为 −1 。我们将创建两个工具函数,分别用于获取和更新节点的高度
/* 获取节点高度 */
int Height(TreeNode? node) {
// 空节点高度为 -1 ,叶节点高度为 0
return node == null ? -1 : node.height;
}
/* 更新节点高度 */
void UpdateHeight(TreeNode node) {
// 节点高度等于最高子树高度 + 1
node.height = Math.Max(Height(node.left), Height(node.right)) + 1;
}
节点的平衡因子定义为节点左子树的高度减去右子树的高度,同时规定空节点的平衡因子为 0
/* 获取平衡因子 */
int BalanceFactor(TreeNode? node) {
// 空节点平衡因子为 0
if (node == null) return 0;
// 节点平衡因子 = 左子树高度 - 右子树高度
return Height(node.left) - Height(node.right);
}
AVL 树的特点在于“旋转”操作,它能够在不影响二叉树的中序遍历序列的前提下,使失衡节点重新恢复平衡。换句话说,**旋转操作既能保持“二叉搜索树”的性质,也能使树重新变为“平衡二叉树”**
右旋
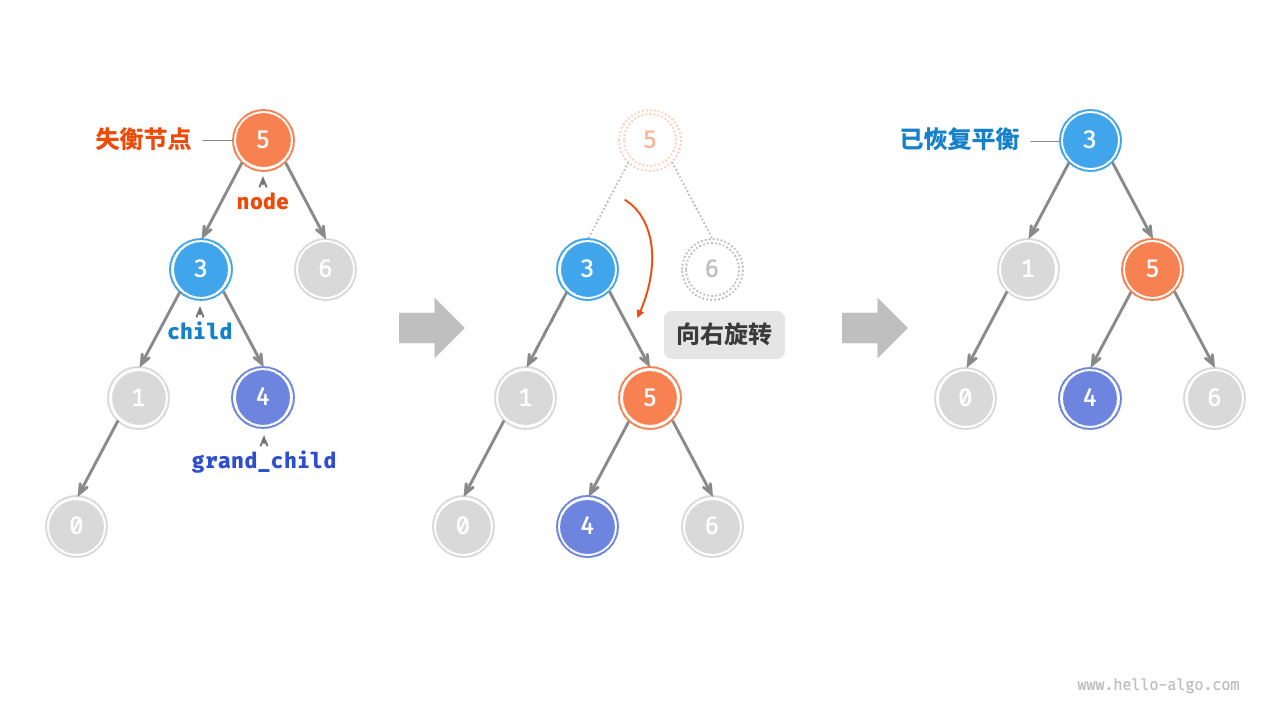
/* 右旋操作 */
TreeNode? RightRotate(TreeNode? node) {
TreeNode? child = node?.left;
TreeNode? grandChild = child?.right;
// 以 child 为原点,将 node 向右旋转
child.right = node;
node.left = grandChild;
// 更新节点高度
UpdateHeight(node);
UpdateHeight(child);
// 返回旋转后子树的根节点
return child;
}
左旋
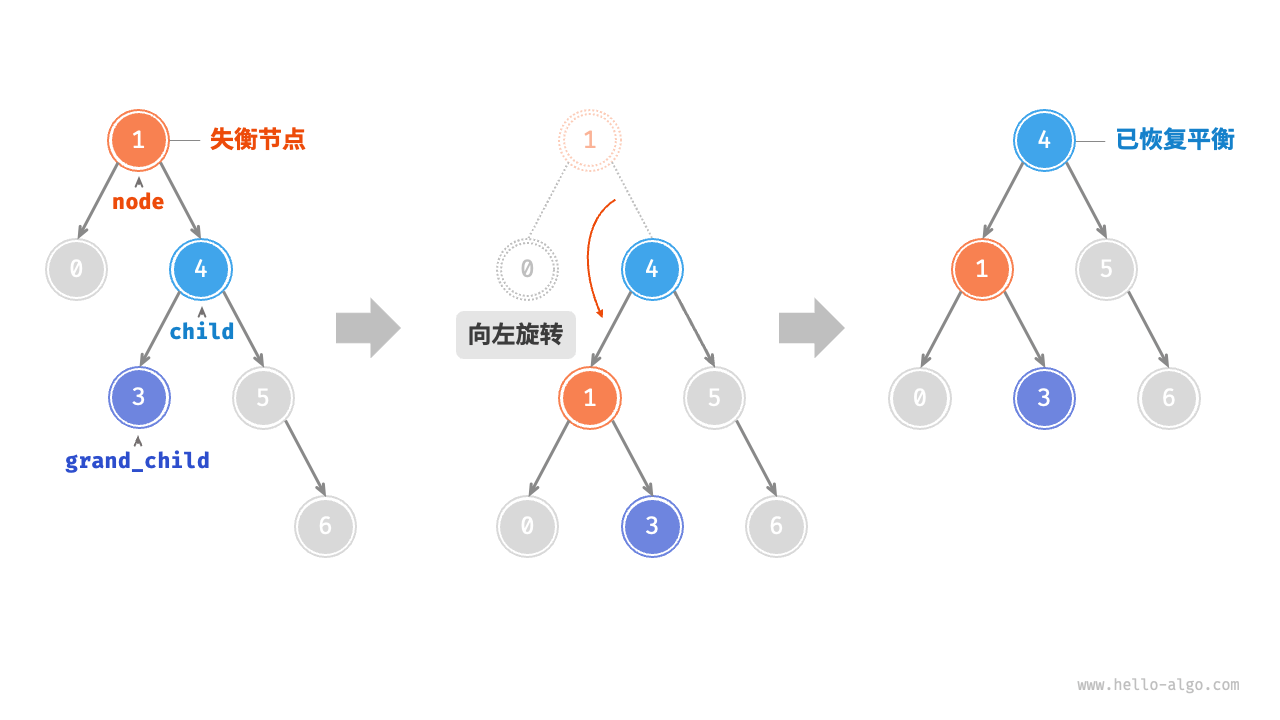
/* 左旋操作 */
TreeNode? LeftRotate(TreeNode? node) {
TreeNode? child = node?.right;
TreeNode? grandChild = child?.left;
// 以 child 为原点,将 node 向左旋转
child.left = node;
node.right = grandChild;
// 更新节点高度
UpdateHeight(node);
UpdateHeight(child);
// 返回旋转后子树的根节点
return child;
}
先左旋再右旋
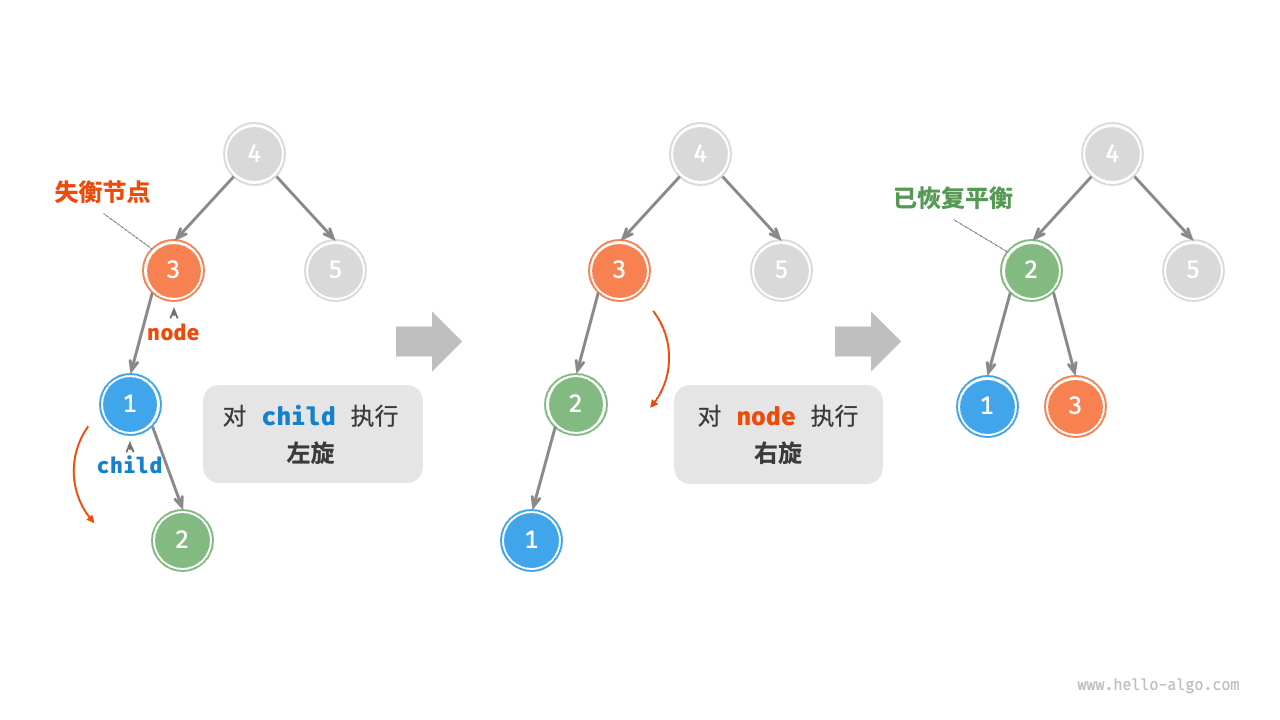
先右旋再左旋
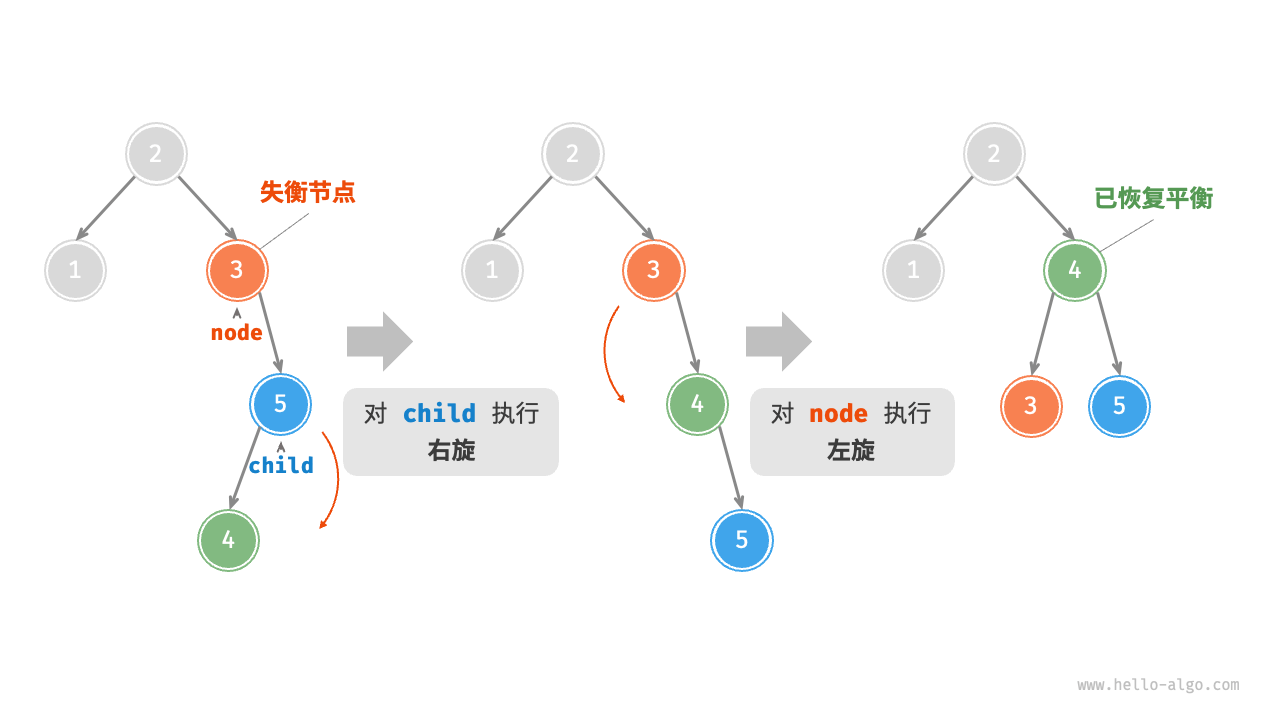
AVL 树的四种旋转情况
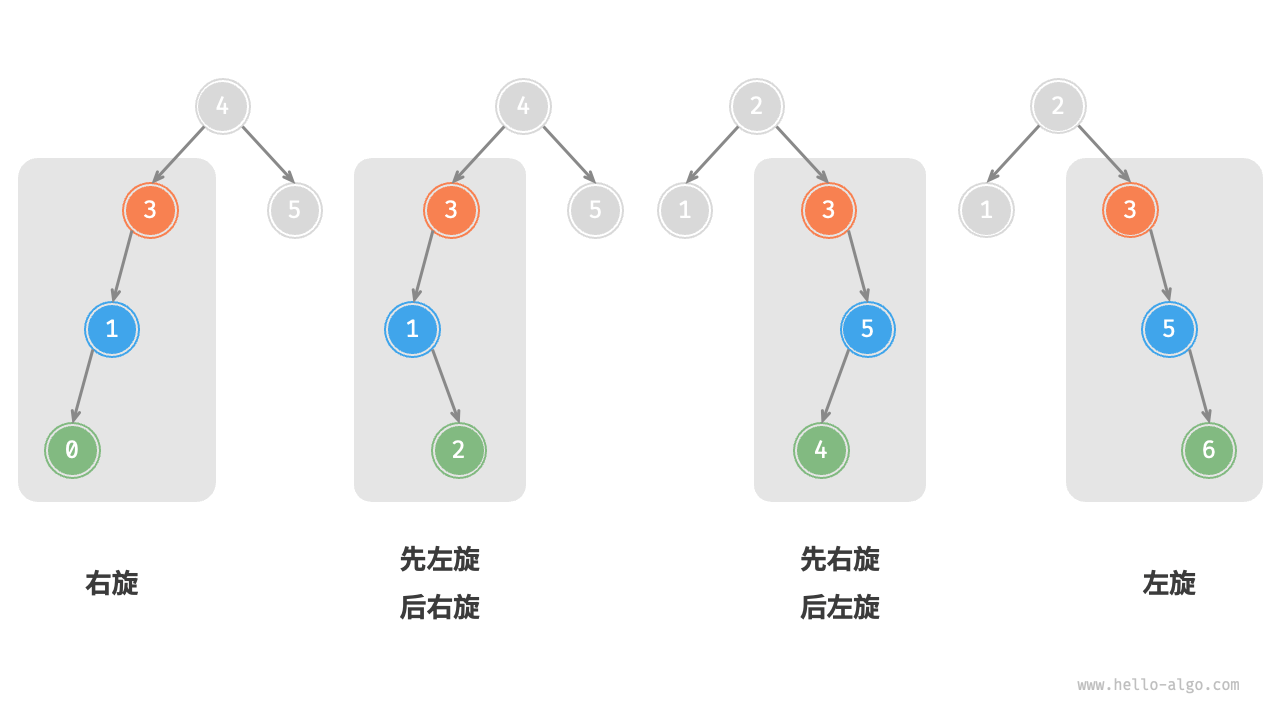
| 失衡节点的平衡因子 | 子节点的平衡因子 | 应采用的旋转方法 |
|---|---|---|
| 右旋 | ||
| 先左旋后右旋 | ||
| 左旋 | ||
| 先右旋后左旋 |
将旋转操作封装成一个函数。有了这个函数,我们就能对各种失衡情况进行旋转,使失衡节点重新恢复平衡
/* 执行旋转操作,使该子树重新恢复平衡 */
TreeNode? Rotate(TreeNode? node) {
// 获取节点 node 的平衡因子
int balanceFactorInt = BalanceFactor(node);
// 左偏树
if (balanceFactorInt > 1) {
if (BalanceFactor(node?.left) >= 0) {
// 右旋
return RightRotate(node);
} else {
// 先左旋后右旋
node!.left = LeftRotate(node!.left);
return RightRotate(node);
}
}
// 右偏树
if (balanceFactorInt < -1) {
if (BalanceFactor(node?.right) <= 0) {
// 左旋
return LeftRotate(node);
} else {
// 先右旋后左旋
node!.right = RightRotate(node!.right);
return LeftRotate(node);
}
}
// 平衡树,无须旋转,直接返回
return node;
}
插入节点
AVL 树的节点插入操作与二叉搜索树在主体上类似。唯一的区别在于,在 AVL 树中插入节点后,从该节点到根节点的路径上可能会出现一系列失衡节点。因此,我们需要从这个节点开始,自底向上执行旋转操作,使所有失衡节点恢复平衡
/* 插入节点 */
void Insert(int val) {
root = InsertHelper(root, val);
}
/* 递归插入节点(辅助方法) */
TreeNode? InsertHelper(TreeNode? node, int val) {
if (node == null) return new TreeNode(val);
/* 1. 查找插入位置并插入节点 */
if (val < node.val)
node.left = InsertHelper(node.left, val);
else if (val > node.val)
node.right = InsertHelper(node.right, val);
else
return node; // 重复节点不插入,直接返回
UpdateHeight(node); // 更新节点高度
/* 2. 执行旋转操作,使该子树重新恢复平衡 */
node = Rotate(node);
// 返回子树的根节点
return node;
}
删除节点
类似地,在二叉搜索树的删除节点方法的基础上,需要从底至顶执行旋转操作,使所有失衡节点恢复平衡
/* 删除节点 */
void Remove(int val) {
root = RemoveHelper(root, val);
}
/* 递归删除节点(辅助方法) */
TreeNode? RemoveHelper(TreeNode? node, int val) {
if (node == null) return null;
/* 1. 查找节点并删除 */
if (val < node.val)
node.left = RemoveHelper(node.left, val);
else if (val > node.val)
node.right = RemoveHelper(node.right, val);
else {
if (node.left == null || node.right == null) {
TreeNode? child = node.left ?? node.right;
// 子节点数量 = 0 ,直接删除 node 并返回
if (child == null)
return null;
// 子节点数量 = 1 ,直接删除 node
else
node = child;
} else {
// 子节点数量 = 2 ,则将中序遍历的下个节点删除,并用该节点替换当前节点
TreeNode? temp = node.right;
while (temp.left != null) {
temp = temp.left;
}
node.right = RemoveHelper(node.right, temp.val!.Value);
node.val = temp.val;
}
}
UpdateHeight(node); // 更新节点高度
/* 2. 执行旋转操作,使该子树重新恢复平衡 */
node = Rotate(node);
// 返回子树的根节点
return node;
}
AVL树典型应用
- 组织和存储大型数据,适用于高频查找、低频增删的场景。
- 用于构建数据库中的索引系统。
- 红黑树也是一种常见的平衡二叉搜索树。相较于 AVL 树,红黑树的平衡条件更宽松,插入与删除节点所需的旋转操作更少,节点增删操作的平均效率更高
堆
堆(heap)是一种满足特定条件的完全二叉树,主要可分为两种类型:
- 小顶堆:任意节点的值 ≤ 其子节点的值。
- 大顶堆:任意节点的值 ≥ 其子节点的值
![]()
堆作为完全二叉树的一个特例,具有以下特性:
- 最底层节点靠左填充,其他层的节点都被填满。
- 我们将二叉树的根节点称为“堆顶”,将底层最靠右的节点称为“堆底”。
- 对于大顶堆(小顶堆),堆顶元素(根节点)的值是最大(最小)的
堆通常用于实现优先队列,大顶堆相当于元素按从大到小的顺序出队的优先队列
/* 初始化堆 */
// 初始化小顶堆
PriorityQueue<int, int> minHeap = new();
// 初始化大顶堆(使用 lambda 表达式修改 Comparer 即可)
PriorityQueue<int, int> maxHeap = new(Comparer<int>.Create((x, y) => y.CompareTo(x)));
/* 元素入堆 */
maxHeap.Enqueue(1, 1);
maxHeap.Enqueue(3, 3);
maxHeap.Enqueue(2, 2);
maxHeap.Enqueue(5, 5);
maxHeap.Enqueue(4, 4);
/* 获取堆顶元素 */
int peek = maxHeap.Peek();//5
/* 堆顶元素出堆 */
// 出堆元素会形成一个从大到小的序列
peek = maxHeap.Dequeue(); // 5
peek = maxHeap.Dequeue(); // 4
peek = maxHeap.Dequeue(); // 3
peek = maxHeap.Dequeue(); // 2
peek = maxHeap.Dequeue(); // 1
/* 获取堆大小 */
int size = maxHeap.Count;
/* 判断堆是否为空 */
bool isEmpty = maxHeap.Count == 0;
/* 输入列表并建堆 */
minHeap = new PriorityQueue<int, int>([(1, 1), (3, 3), (2, 2), (5, 5), (4, 4)]);
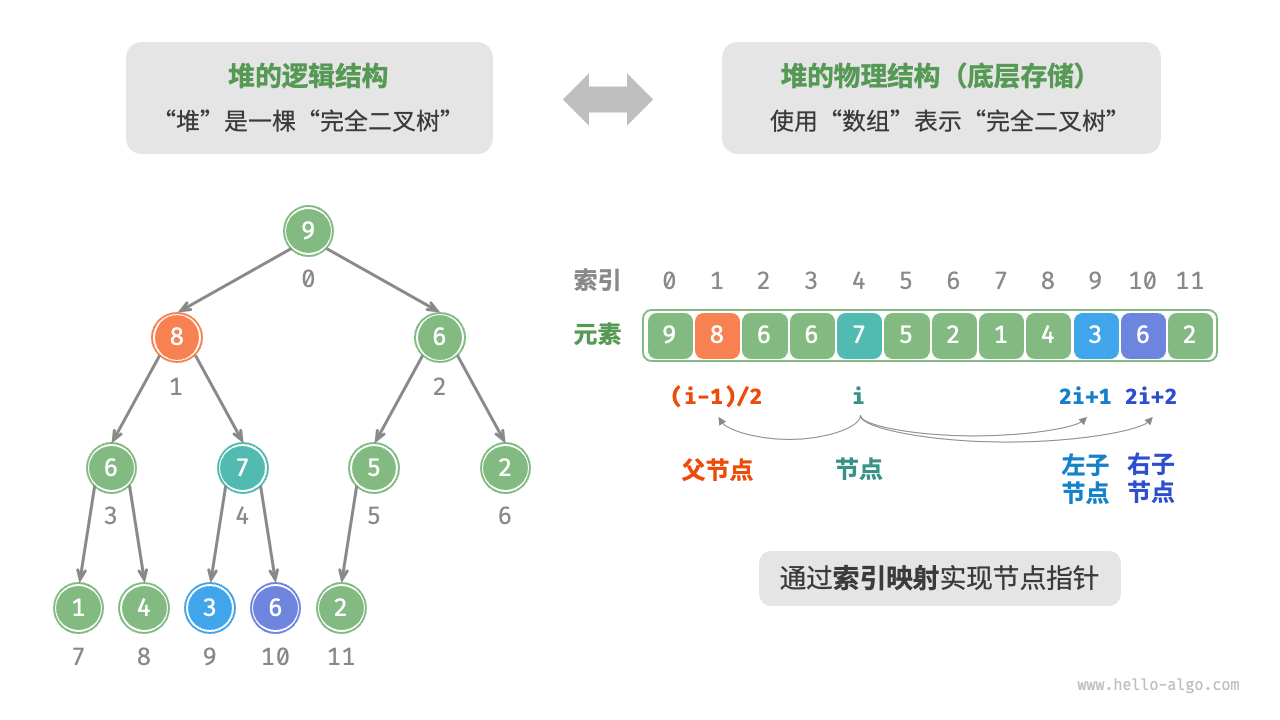
当使用数组表示二叉树时,元素代表节点值,索引代表节点在二叉树中的位置。节点指针通过索引映射公式来实现。
给定索引 i ,其左子节点的索引为 2i+1 ,右子节点的索引为 2i+2 ,父节点的索引为 (i−1)/2(向下整除)。当索引越界时,表示空节点或节点不存在
/* 获取左子节点的索引 */
int Left(int i) {
return 2 * i + 1;
}
/* 获取右子节点的索引 */
int Right(int i) {
return 2 * i + 2;
}
/* 获取父节点的索引 */
int Parent(int i) {
return (i - 1) / 2; // 向下整除
}
/* 访问堆顶元素 */
int Peek() {
return maxHeap[0];
}
给定元素 val ,首先将其添加到堆底。添加之后,由于 val 可能大于堆中其他元素,堆的成立条件可能已被破坏,因此需要修复从插入节点到根节点的路径上的各个节点,这个操作被称为堆化
设节点总数为 n ,则树的高度为 O(logn) 。由此可知,堆化操作的循环轮数最多为 O(logn) ,元素入堆操作的时间复杂度为O(logn)
/* 元素入堆 */
void Push(int val) {
// 添加节点
maxHeap.Add(val);
// 从底至顶堆化
SiftUp(Size() - 1);
}
/* 从节点 i 开始,从底至顶堆化 */
void SiftUp(int i) {
while (true) {
// 获取节点 i 的父节点
int p = Parent(i);
// 若“越过根节点”或“节点无须修复”,则结束堆化
if (p < 0 || maxHeap[i] <= maxHeap[p])
break;
// 交换两节点
Swap(i, p);
// 循环向上堆化
i = p;
}
}
堆顶元素是二叉树的根节点,即列表首元素。如果我们直接从列表中删除首元素,那么二叉树中所有节点的索引都会发生变化,这将使得后续使用堆化进行修复变得困难。为了尽量减少元素索引的变动,我们采用以下操作步骤:
- 交换堆顶元素与堆底元素(交换根节点与最右叶节点)。
- 交换完成后,将堆底从列表中删除(注意,由于已经交换,因此实际上删除的是原来的堆顶元素)。
- 从根节点开始,从顶至底执行堆化
/* 元素出堆 */
int Pop() {
// 判空处理
if (IsEmpty())
throw new IndexOutOfRangeException();
// 交换根节点与最右叶节点(交换首元素与尾元素)
Swap(0, Size() - 1);
// 删除节点
int val = maxHeap.Last();
maxHeap.RemoveAt(Size() - 1);
// 从顶至底堆化
SiftDown(0);
// 返回堆顶元素
return val;
}
/* 从节点 i 开始,从顶至底堆化 */
void SiftDown(int i) {
while (true) {
// 判断节点 i, l, r 中值最大的节点,记为 ma
int l = Left(i), r = Right(i), ma = i;
if (l < Size() && maxHeap[l] > maxHeap[ma])
ma = l;
if (r < Size() && maxHeap[r] > maxHeap[ma])
ma = r;
// 若“节点 i 最大”或“越过叶节点”,则结束堆化
if (ma == i) break;
// 交换两节点
Swap(i, ma);
// 循环向下堆化
i = ma;
}
}
*堆的常见应用
- 优先队列:堆通常作为实现优先队列的首选数据结构,其入队和出队操作的时间复杂度均为 O(logn) ,而建堆操作为 O(n) ,这些操作都非常高效。
- 堆排序:给定一组数据,我们可以用它们建立一个堆,然后不断地执行元素出堆操作,从而得到有序数据。然而,我们通常会使用一种更优雅的方式实现堆排序,详见“堆排序”章节。
- 获取最大的 k 个元素:这是一个经典的算法问题,同时也是一种典型应用,例如选择热度前 10 的新闻作为微博热搜,选取销量前 10 的商品等
可以基于堆更加高效地解决 Top-k 问题:
- 初始化一个小顶堆,其堆顶元素最小。
- 先将数组的前 k 个元素依次入堆。
- 从第 k+1 个元素开始,若当前元素大于堆顶元素,则将堆顶元素出堆,并将当前元素入堆。
- 遍历完成后,堆中保存的就是最大的 k 个元素
/* 基于堆查找数组中最大的 k 个元素 */
PriorityQueue<int, int> TopKHeap(int[] nums, int k) {
// 初始化小顶堆
PriorityQueue<int, int> heap = new();
// 将数组的前 k 个元素入堆
for (int i = 0; i < k; i++) {
heap.Enqueue(nums[i], nums[i]);
}
// 从第 k+1 个元素开始,保持堆的长度为 k
for (int i = k; i < nums.Length; i++) {
// 若当前元素大于堆顶元素,则将堆顶元素出堆、当前元素入堆
if (nums[i] > heap.Peek()) {
heap.Dequeue();
heap.Enqueue(nums[i], nums[i]);
}
}
return heap;
}
图
图是一种非线性数据结构,由顶点(vertex)和边(edge)组成。我们可以将图 G 抽象地表示为一组顶点 V 和一组边 E 的集合
以下示例展示了一个包含 5 个顶点和 7 条边的图:
$$
\begin{align}
V &= {1, 2, 3, 4, 5} \
E &= {(1, 2), (1, 3), (1, 5), (2, 3), (2, 4), (2, 5), (4, 5)} \
G &= {V, E}
\end{align}
$$
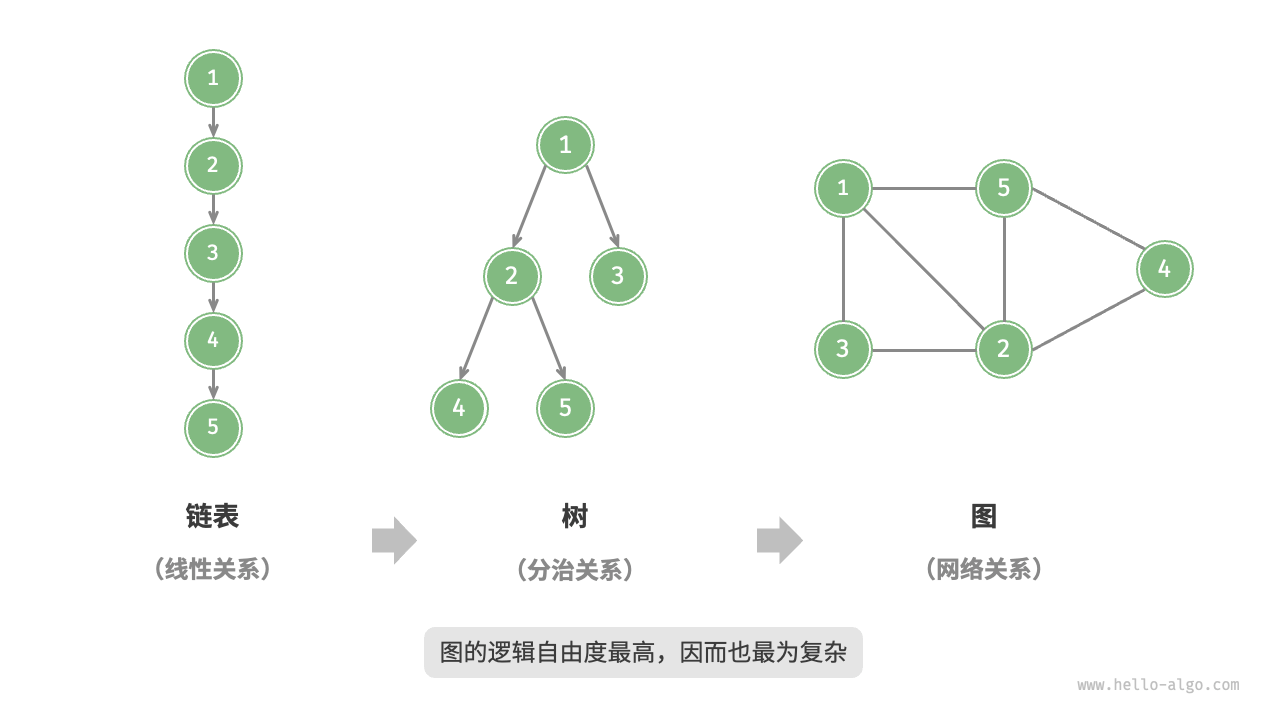
根据边是否有方向,分为无向图(undirected graph)和有向图(directed graph)
- 在无向图中,边表示两顶点之间的“双向”连接关系,例如微信或 QQ 中的“好友关系”。
- 在有向图中,边具有方向性,即 A→B 和 A←B 两个方向的边是相互独立的,例如哔哩哔哩上的“关注”与“被关注”关系
![]()
根据边是否有方向,分为非连通图(disconnected graph)和连通图(connected graph)
- 对于连通图,从某个顶点出发,可以到达其余任意顶点。
- 对于非连通图,从某个顶点出发,至少有一个顶点无法到达
![]()
还可以为边添加权重,从而达到有权图(weighted graph),比如游戏中的亲密度网络
图数据结构包含以下常用术语:
- 邻接
(adjacency):当两顶点之间存在边相连时,称这两顶点“邻接”。在上图中,顶点 1 的邻接顶点为顶点 2、3、5 - 路径
(path):从顶点 A 到顶点 B 经过的边构成的序列被称为从 A 到 B 的“路径”。在上图中,边序列 1-5-2-4 是顶点 1 到顶点 4 的一条路径 - 度
(degree):一个顶点拥有的边数。对于有向图,入度(in-degree)表示有多少条边指向该顶点,出度(out-degree)表示有多少条边从该顶点指出
*图的常用表示方式包括"邻接矩阵"和"邻接表"
- 邻矩阵
设图的顶点数量为 n ,邻接矩阵使用一个 n*n 大小的矩阵来表示图,每一行(列)代表一个顶点,矩阵元素代表边,用 1 或 0 表示两个顶点之间是否存在边。
![]()
如图所示,设邻接矩阵为 M、顶点列表为 V ,那么矩阵元素 M[i,j]=1 表示顶点 V[i] 到顶点 V[j] 之间存在边,反之 M[i,j]=0 表示两顶点之间无边
邻接矩阵具有以下特性:
- 在简单图中,顶点不能与自身相连,此时邻接矩阵主对角线元素没有意义。
- 对于无向图,两个方向的边等价,此时邻接矩阵关于主对角线对称。
- 将邻接矩阵的元素从 1 和 0 替换为权重,则可表示有权图。
使用邻接矩阵表示图时,可以直接访问矩阵元素以获取边,因此增删查改操作的效率很高,时间复杂度均为 O(1) 。然而,矩阵的空间复杂度为 $O(n^2)$ ,内存占用较多
-
邻接表
邻接表使用 n 个链表来表示图,链表节点表示顶点。第 i 个链表对应顶点 i ,其中存储了该顶点的所有邻接顶点(与该顶点相连的顶点)
![]()
邻接表仅存储实际存在的边,而边的总数通常远小于 $n^2$ ,因此它更加节省空间。然而,在邻接表中需要通过遍历链表来查找边,因此其时间效率不如邻接矩阵邻接表结构与哈希表中的“链式地址”非常相似,因此我们也可以采用类似的方法来优化效率。比如当链表较长时,可以将链表转化为 AVL 树或红黑树,从而将时间效率从 O(n) 优化至 O(logn) ;还可以把链表转换为哈希表,从而将时间复杂度降至 O(1)
基于邻接矩阵的实现
给定一个顶点数量为 n 的无向图,则各种操作的实现方式如下图所示
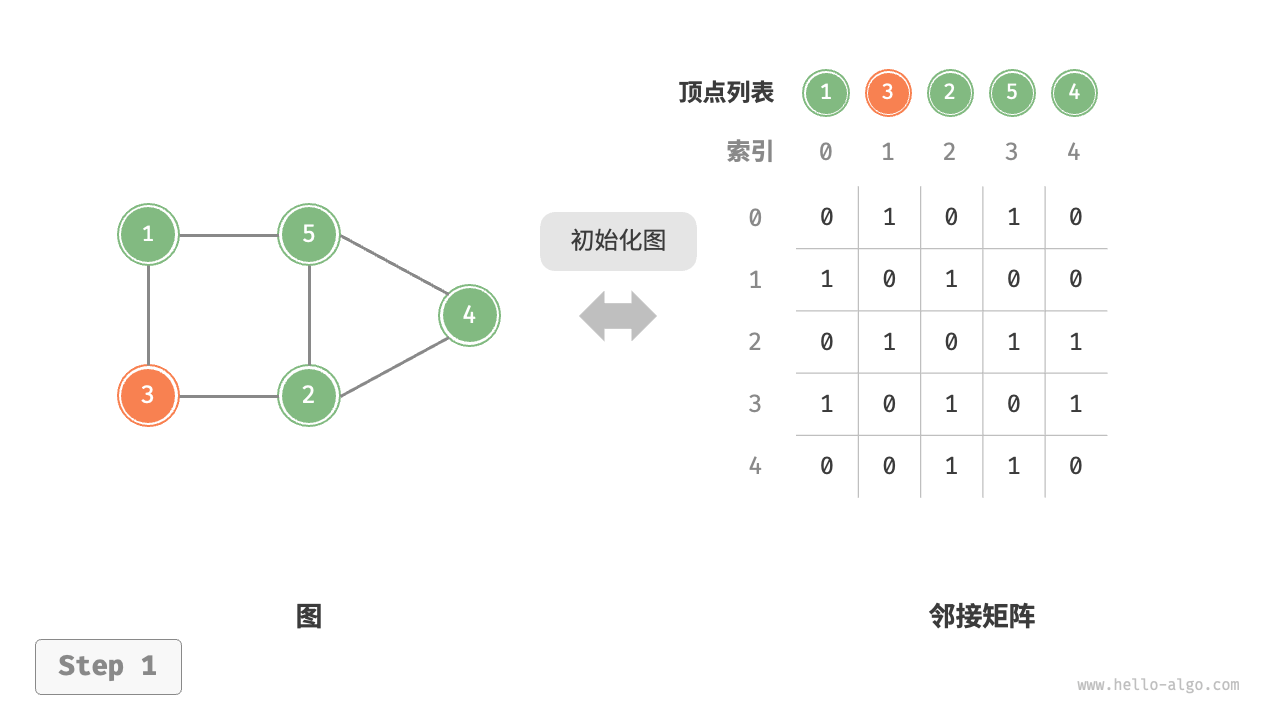
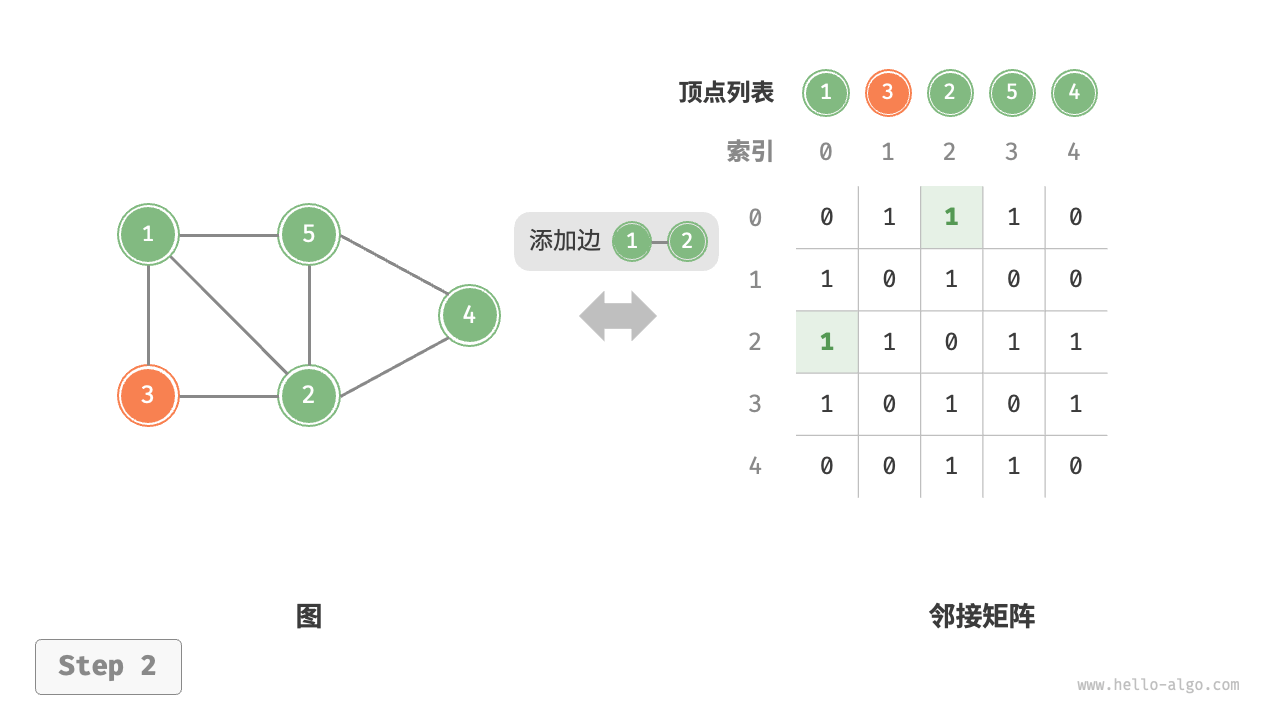
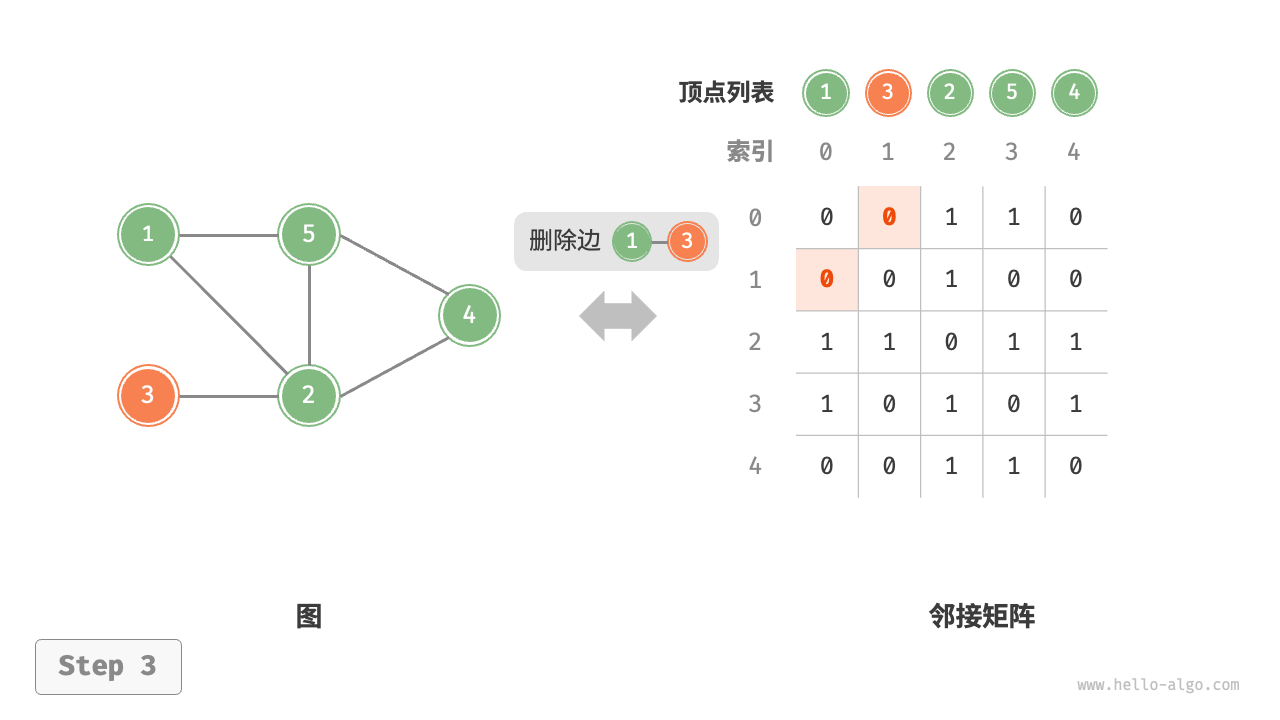
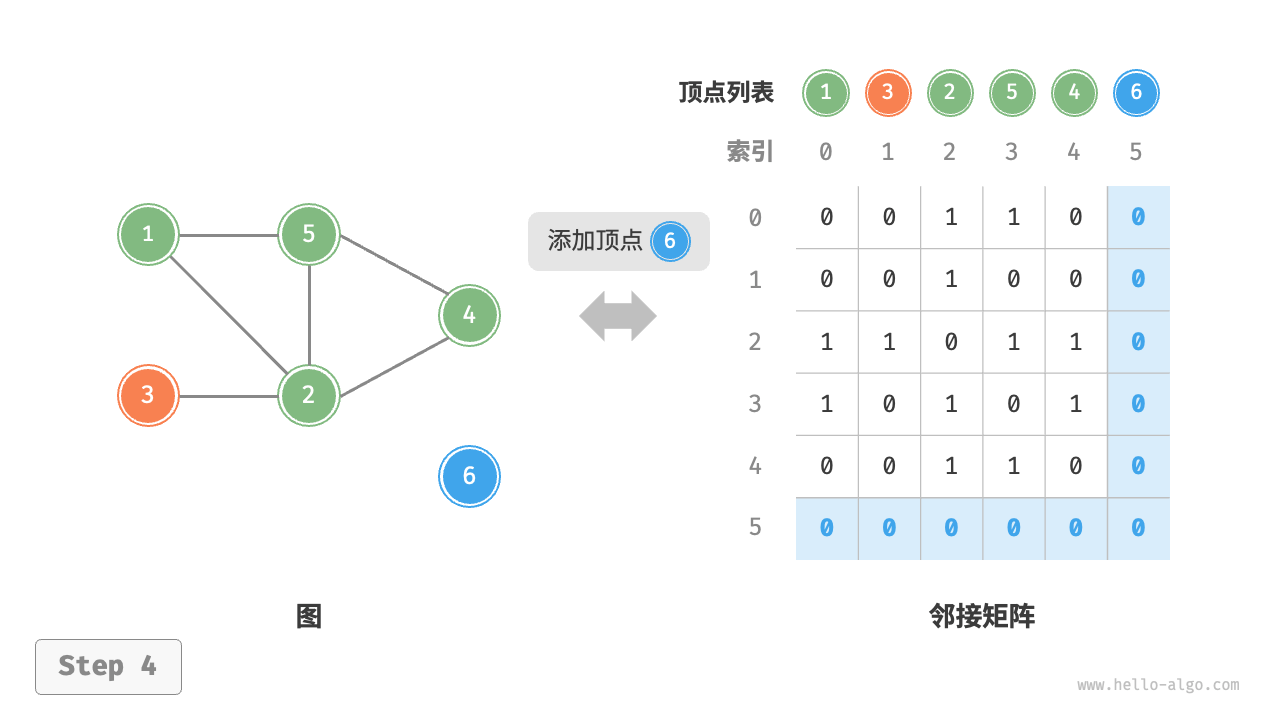
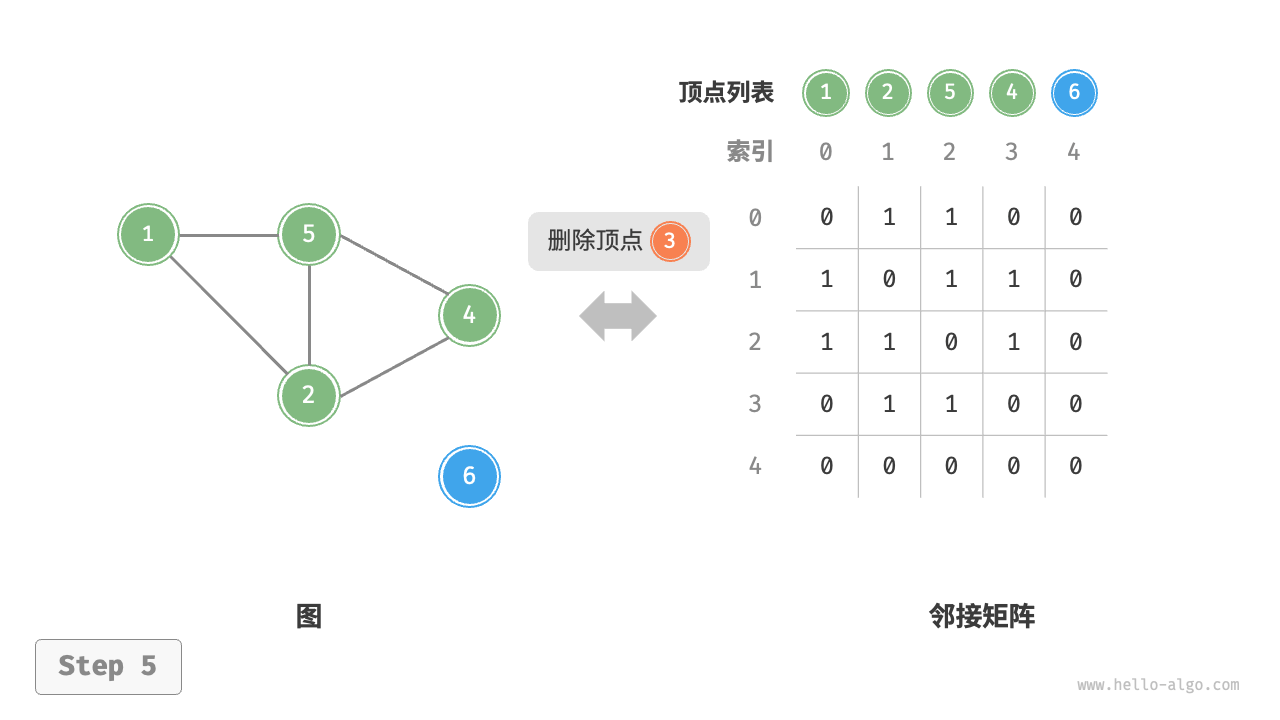
- 添加或删除边:直接在邻接矩阵中修改指定的边即可,使用 O(1) 时间。而由于是无向图,因此需要同时更新两个方向的边。
- 添加顶点:在邻接矩阵的尾部添加一行一列,并全部填 0 即可,使用 O(n) 时间。
- 删除顶点:在邻接矩阵中删除一行一列。当删除首行首列时达到最差情况,需要将 $(n−1)^2$ 个元素“向左上移动”,从而使用 $O(n^2)$ 时间。
- 初始化:传入 n 个顶点,初始化长度为 n 的顶点列表
vertices,使用 O(n) 时间;初始化 n*n 大小的邻接矩阵adjMat,使用 $O(n^2)$ 时间。
/* 基于邻接矩阵实现的无向图类 */
class GraphAdjMat {
List<int> vertices; // 顶点列表,元素代表“顶点值”,索引代表“顶点索引”
List<List<int>> adjMat; // 邻接矩阵,行列索引对应“顶点索引”
/* 构造函数 */
public GraphAdjMat(int[] vertices, int[][] edges) {
this.vertices = [];
this.adjMat = [];
// 添加顶点
foreach (int val in vertices) {
AddVertex(val);
}
// 添加边
// 请注意,edges 元素代表顶点索引,即对应 vertices 元素索引
foreach (int[] e in edges) {
AddEdge(e[0], e[1]);
}
}
/* 获取顶点数量 */
int Size() {
return vertices.Count;
}
/* 添加顶点 */
public void AddVertex(int val) {
int n = Size();
// 向顶点列表中添加新顶点的值
vertices.Add(val);
// 在邻接矩阵中添加一行
List<int> newRow = new(n);
for (int j = 0; j < n; j++) {
newRow.Add(0);
}
adjMat.Add(newRow);
// 在邻接矩阵中添加一列
foreach (List<int> row in adjMat) {
row.Add(0);
}
}
/* 删除顶点 */
public void RemoveVertex(int index) {
if (index >= Size())
throw new IndexOutOfRangeException();
// 在顶点列表中移除索引 index 的顶点
vertices.RemoveAt(index);
// 在邻接矩阵中删除索引 index 的行
adjMat.RemoveAt(index);
// 在邻接矩阵中删除索引 index 的列
foreach (List<int> row in adjMat) {
row.RemoveAt(index);
}
}
/* 添加边 */
// 参数 i, j 对应 vertices 元素索引
public void AddEdge(int i, int j) {
// 索引越界与相等处理
if (i < 0 || j < 0 || i >= Size() || j >= Size() || i == j)
throw new IndexOutOfRangeException();
// 在无向图中,邻接矩阵关于主对角线对称,即满足 (i, j) == (j, i)
adjMat[i][j] = 1;
adjMat[j][i] = 1;
}
/* 删除边 */
// 参数 i, j 对应 vertices 元素索引
public void RemoveEdge(int i, int j) {
// 索引越界与相等处理
if (i < 0 || j < 0 || i >= Size() || j >= Size() || i == j)
throw new IndexOutOfRangeException();
adjMat[i][j] = 0;
adjMat[j][i] = 0;
}
/* 打印邻接矩阵 */
public void Print() {
Console.Write("顶点列表 = ");
PrintUtil.PrintList(vertices);
Console.WriteLine("邻接矩阵 =");
PrintUtil.PrintMatrix(adjMat);
}
}
基于邻接表的实现
设无向图的顶点总数为 n、边总数为 m ,则各种操作的实现方式如下图所示
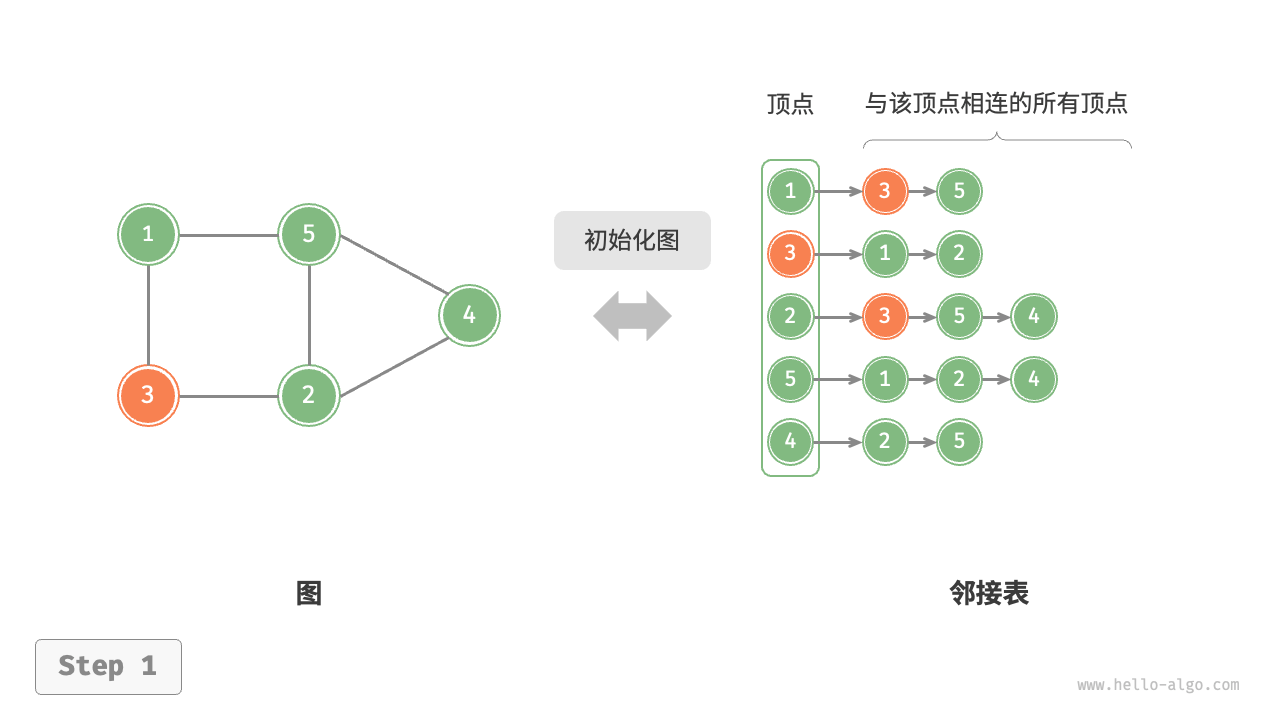
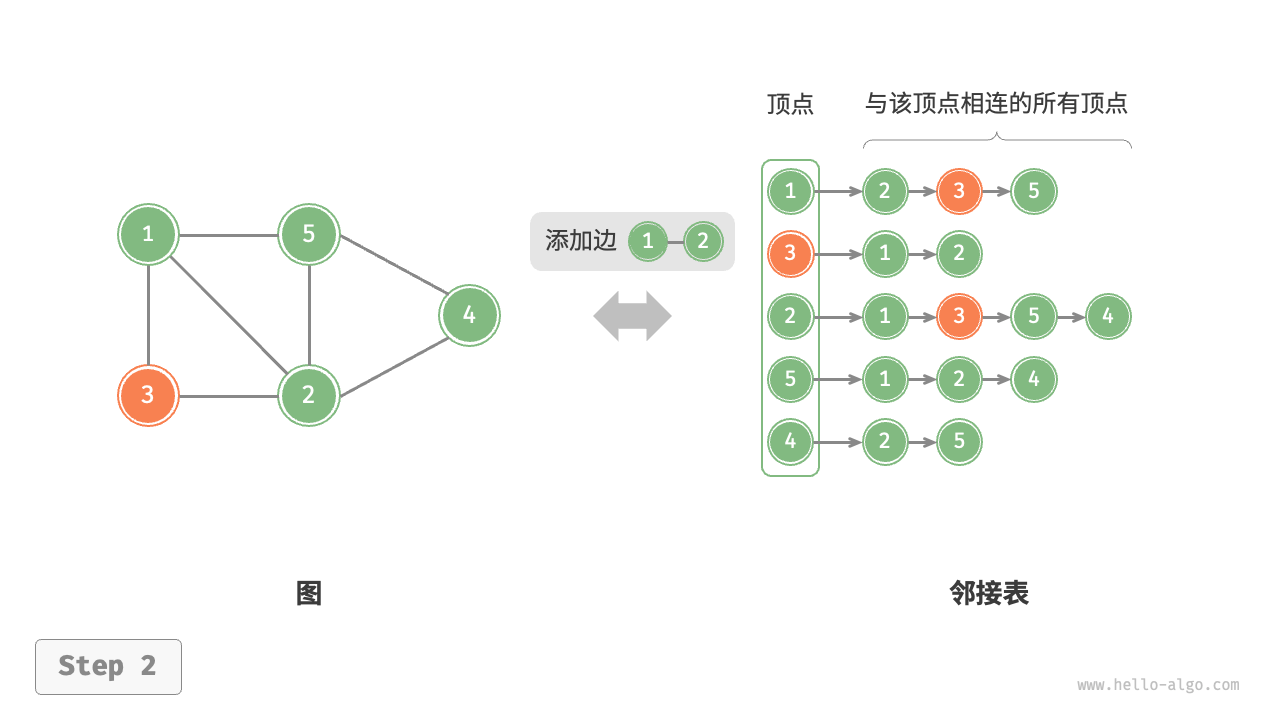
-
添加边:在顶点对应链表的末尾添加边即可,使用 O(1) 时间。因为是无向图,所以需要同时添加两个方向的边。
-
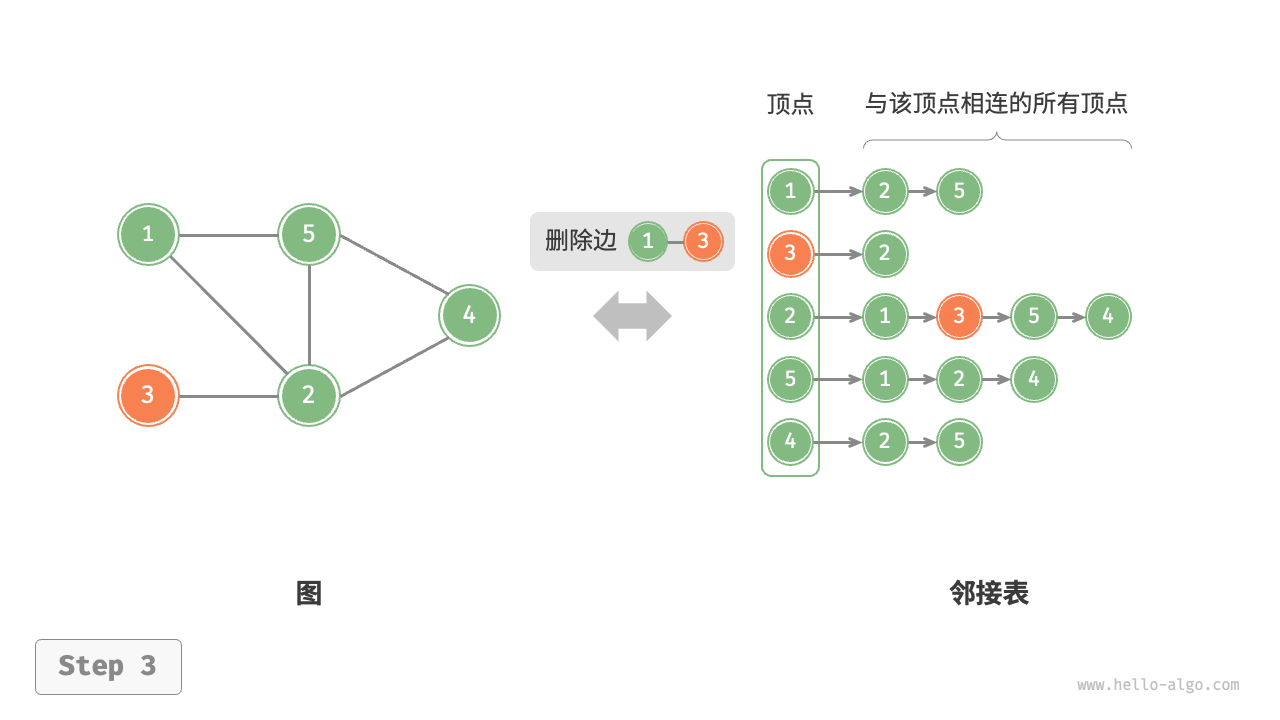
删除边:在顶点对应链表中查找并删除指定边,使用 O(m) 时间。在无向图中,需要同时删除两个方向的边。
-
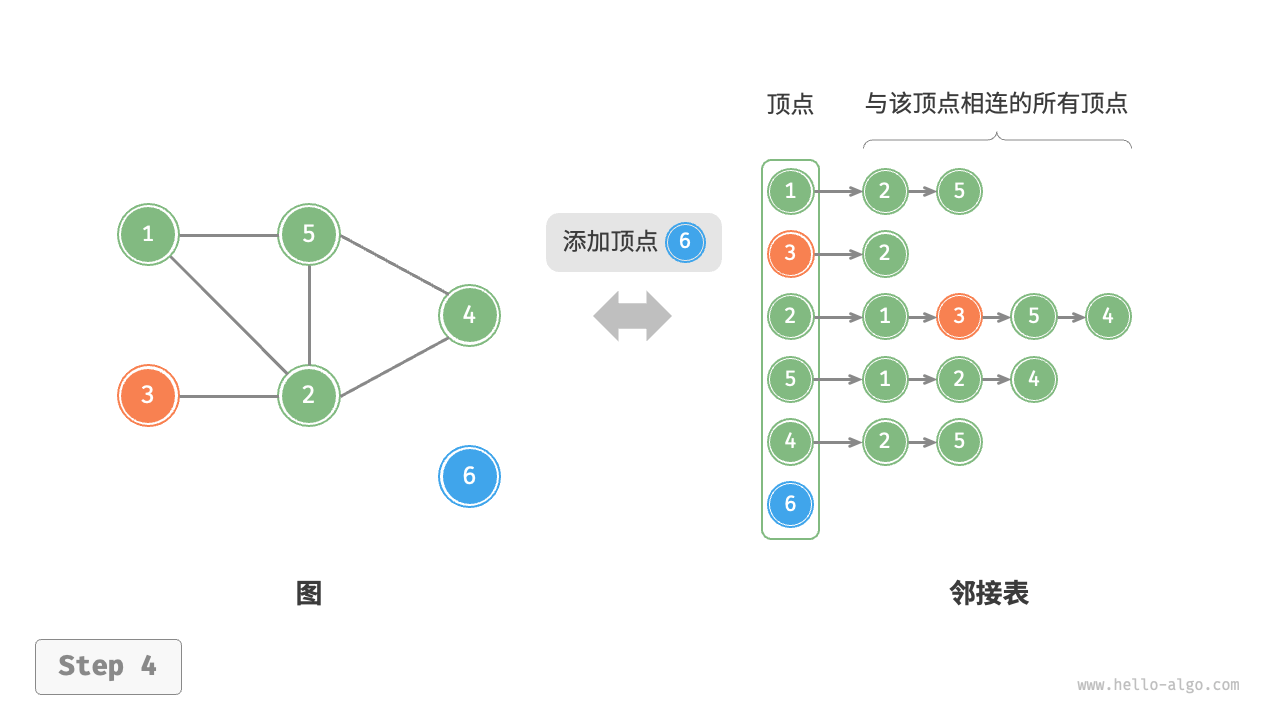
添加顶点:在邻接表中添加一个链表,并将新增顶点作为链表头节点,使用 O(1) 时间。
-
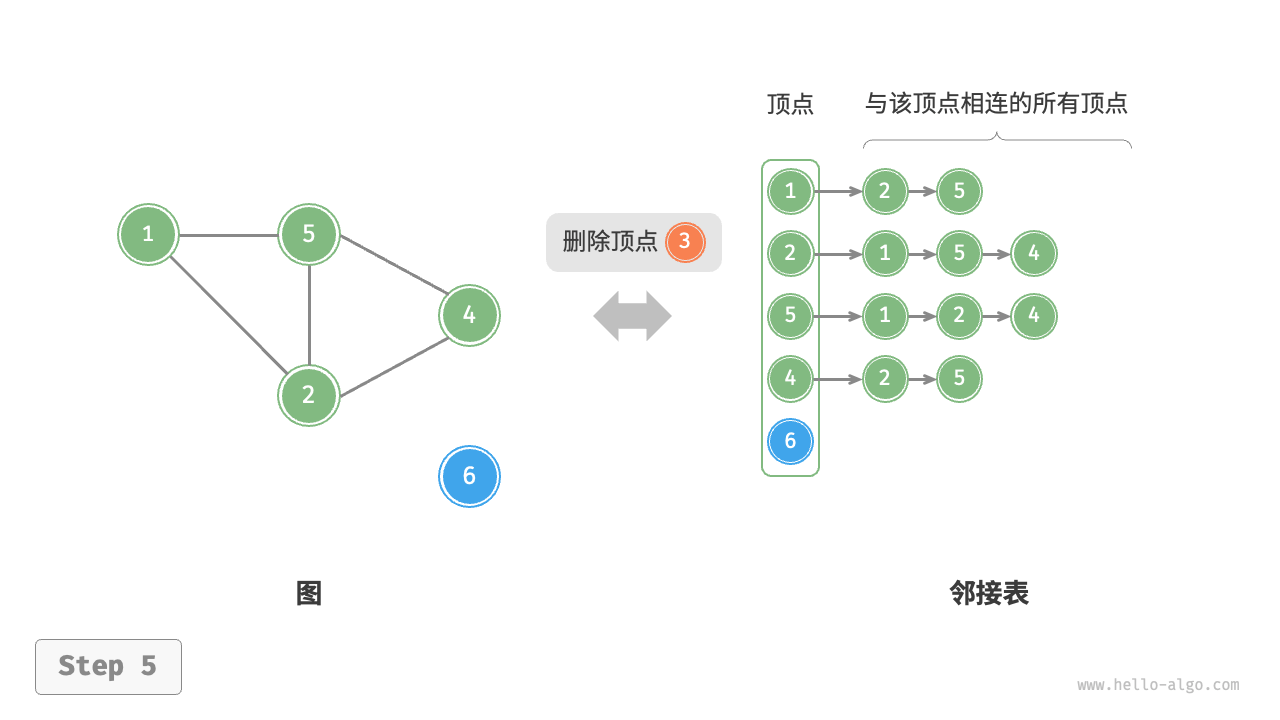
删除顶点:需遍历整个邻接表,删除包含指定顶点的所有边,使用 O(n+m) 时间。
-
初始化:在邻接表中创建 n 个顶点和 2m 条边,使用 O(n+m) 时间。
-
为了方便添加与删除顶点,以及简化代码,我们使用列表(动态数组)来代替链表。
-
使用哈希表来存储邻接表,
key为顶点实例,value为该顶点的邻接顶点列表(链表)。
另外,我们在邻接表中使用 Vertex 类来表示顶点,这样做的原因是:如果与邻接矩阵一样,用列表索引来区分不同顶点,那么假设要删除索引为 i 的顶点,则需遍历整个邻接表,将所有大于 i 的索引全部减 1 ,效率很低。而如果每个顶点都是唯一的 Vertex 实例,删除某一顶点之后就无须改动其他顶点了
/* 基于邻接表实现的无向图类 */
class GraphAdjList {
// 邻接表,key:顶点,value:该顶点的所有邻接顶点
public Dictionary<Vertex, List<Vertex>> adjList;
/* 构造函数 */
public GraphAdjList(Vertex[][] edges) {
adjList = [];
// 添加所有顶点和边
foreach (Vertex[] edge in edges) {
AddVertex(edge[0]);
AddVertex(edge[1]);
AddEdge(edge[0], edge[1]);
}
}
/* 获取顶点数量 */
int Size() {
return adjList.Count;
}
/* 添加边 */
public void AddEdge(Vertex vet1, Vertex vet2) {
if (!adjList.ContainsKey(vet1) || !adjList.ContainsKey(vet2) || vet1 == vet2)
throw new InvalidOperationException();
// 添加边 vet1 - vet2
adjList[vet1].Add(vet2);
adjList[vet2].Add(vet1);
}
/* 删除边 */
public void RemoveEdge(Vertex vet1, Vertex vet2) {
if (!adjList.ContainsKey(vet1) || !adjList.ContainsKey(vet2) || vet1 == vet2)
throw new InvalidOperationException();
// 删除边 vet1 - vet2
adjList[vet1].Remove(vet2);
adjList[vet2].Remove(vet1);
}
/* 添加顶点 */
public void AddVertex(Vertex vet) {
if (adjList.ContainsKey(vet))
return;
// 在邻接表中添加一个新链表
adjList.Add(vet, []);
}
/* 删除顶点 */
public void RemoveVertex(Vertex vet) {
if (!adjList.ContainsKey(vet))
throw new InvalidOperationException();
// 在邻接表中删除顶点 vet 对应的链表
adjList.Remove(vet);
// 遍历其他顶点的链表,删除所有包含 vet 的边
foreach (List<Vertex> list in adjList.Values) {
list.Remove(vet);
}
}
/* 打印邻接表 */
public void Print() {
Console.WriteLine("邻接表 =");
foreach (KeyValuePair<Vertex, List<Vertex>> pair in adjList) {
List<int> tmp = [];
foreach (Vertex vertex in pair.Value)
tmp.Add(vertex.val);
Console.WriteLine(pair.Key.val + ": [" + string.Join(", ", tmp) + "],");
}
}
}
设图中共有 n 个顶点和 m 条边,对比邻接矩阵和邻接表的时间效率和空间效率
| 邻接矩阵 | 邻接表(链表) | 邻接表(哈希表) | |
|---|---|---|---|
| 判断是否邻接 | |||
| 添加边 | |||
| 删除边 | |||
| 添加顶点 | |||
| 删除顶点 | |||
| 内存空间占用 |
图的遍历
- 广度优先遍历
广度优先遍历是一种由近及远的遍历方式,从某个节点触发,始终优先访问距离最近的顶点,并一层层向外扩张
![]()
BFS 通常借助队列来实现,代码如下所示。队列具有“先入先出”的性质,这与 BFS 的“由近及远”的思想异曲同工 - 将遍历起始顶点
startVet加入队列,并开启循环。 - 在循环的每轮迭代中,弹出队首顶点并记录访问,然后将该顶点的所有邻接顶点加入到队列尾部。
- 循环步骤
2.,直到所有顶点被访问完毕后结束。
为了防止重复遍历顶点,需要借助一个哈希集合visited来记录哪些节点已被访问
/* 广度优先遍历 */
// 使用邻接表来表示图,以便获取指定顶点的所有邻接顶点
List<Vertex> GraphBFS(GraphAdjList graph, Vertex startVet) {
// 顶点遍历序列
List<Vertex> res = [];
// 哈希集合,用于记录已被访问过的顶点
HashSet<Vertex> visited = [startVet];
// 队列用于实现 BFS
Queue<Vertex> que = new();
que.Enqueue(startVet);
// 以顶点 vet 为起点,循环直至访问完所有顶点
while (que.Count > 0) {
Vertex vet = que.Dequeue(); // 队首顶点出队
res.Add(vet); // 记录访问顶点
foreach (Vertex adjVet in graph.adjList[vet]) {
if (visited.Contains(adjVet)) {
continue; // 跳过已被访问的顶点
}
que.Enqueue(adjVet); // 只入队未访问的顶点
visited.Add(adjVet); // 标记该顶点已被访问
}
}
// 返回顶点遍历序列
return res;
}
图的广度优先遍历步骤
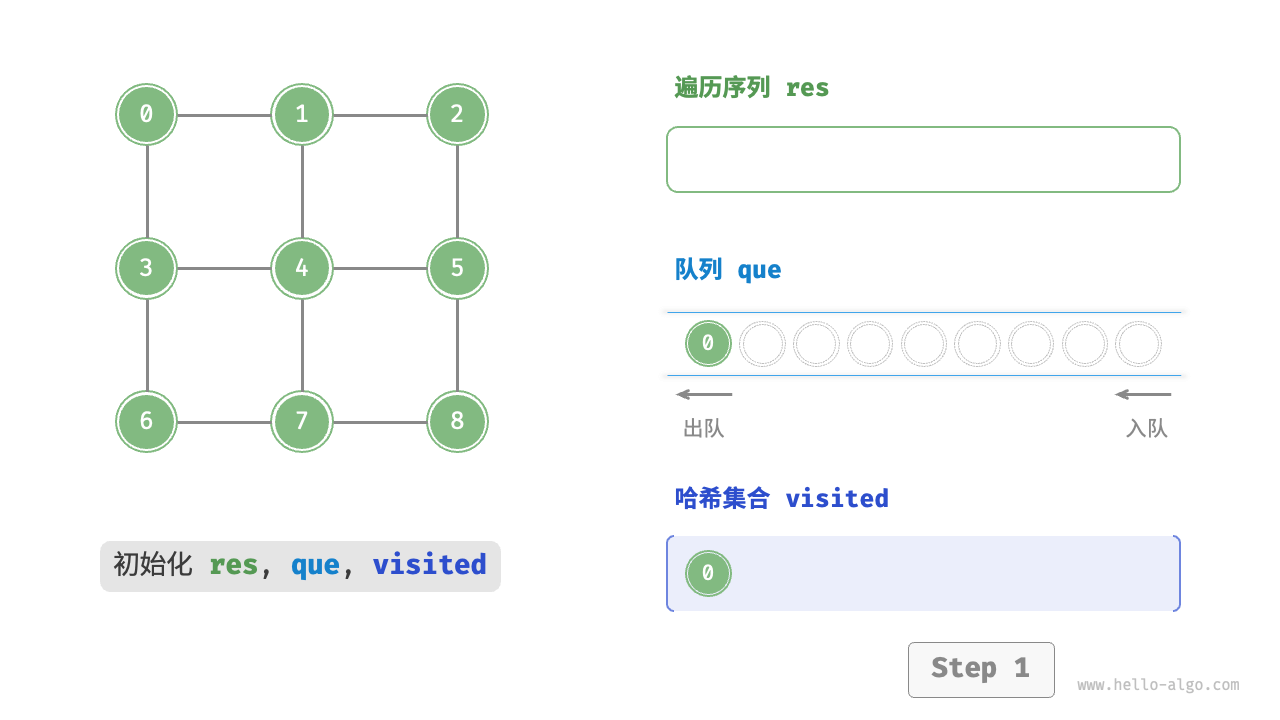
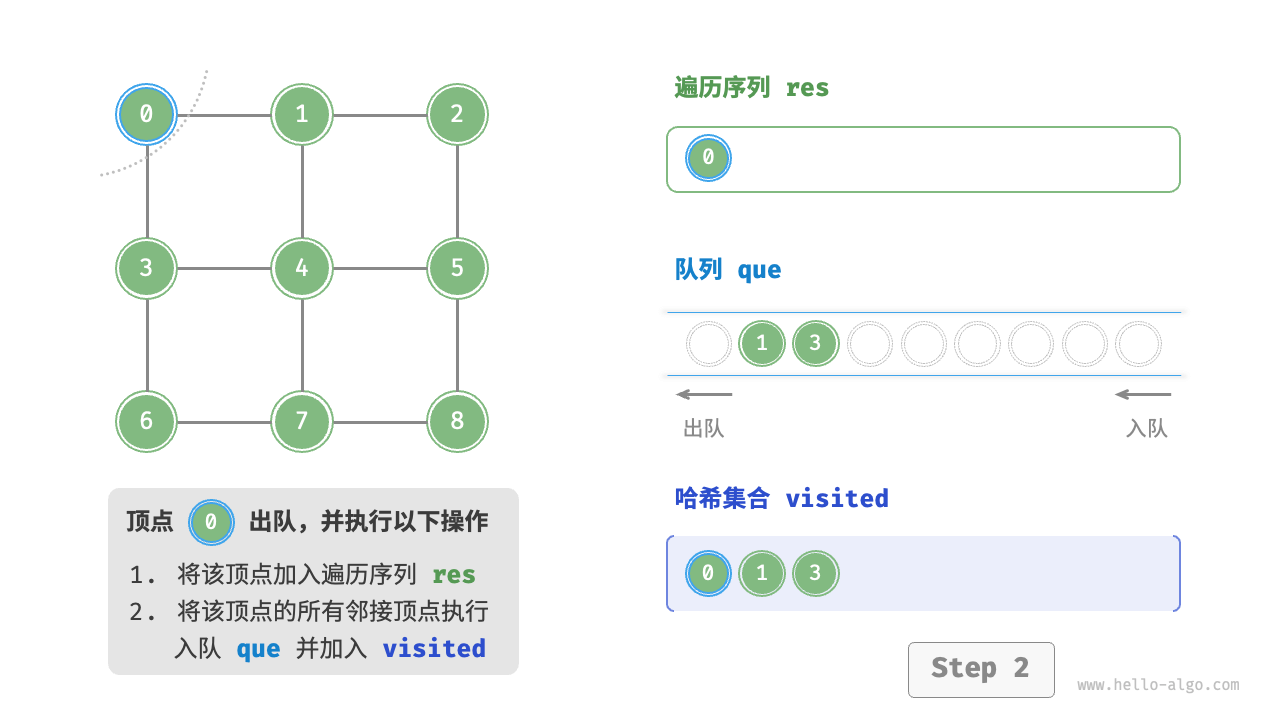
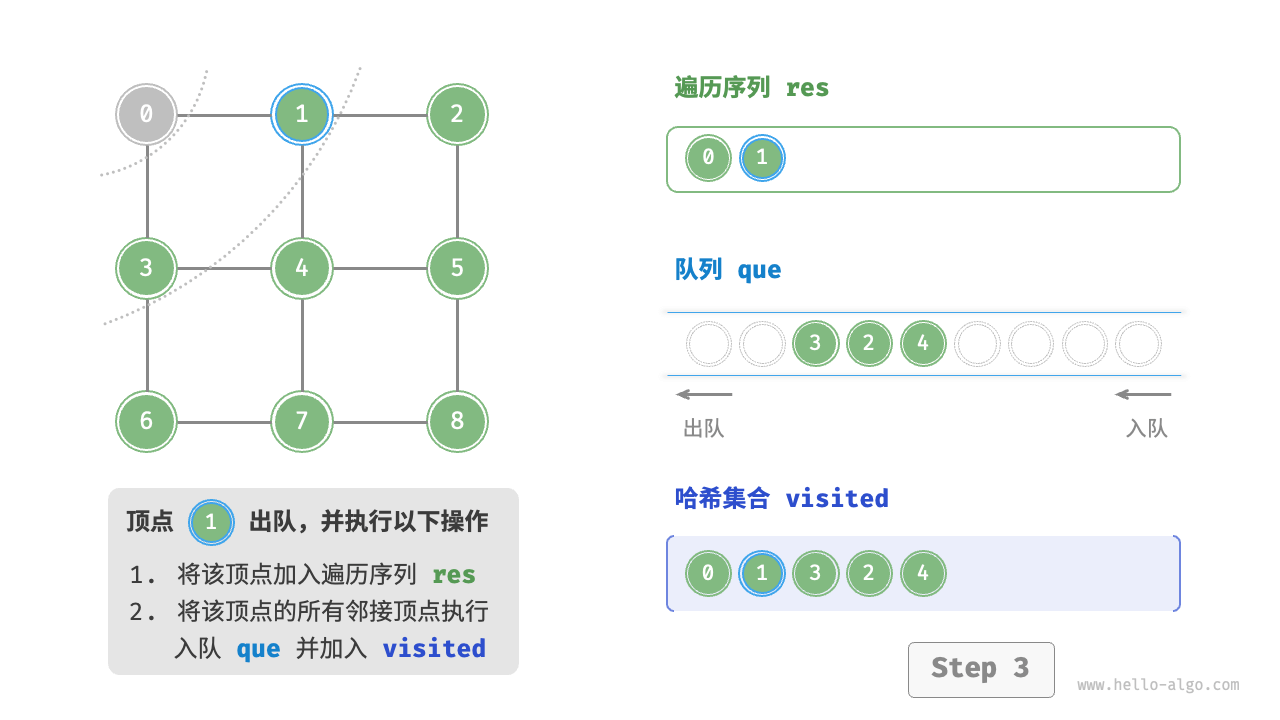
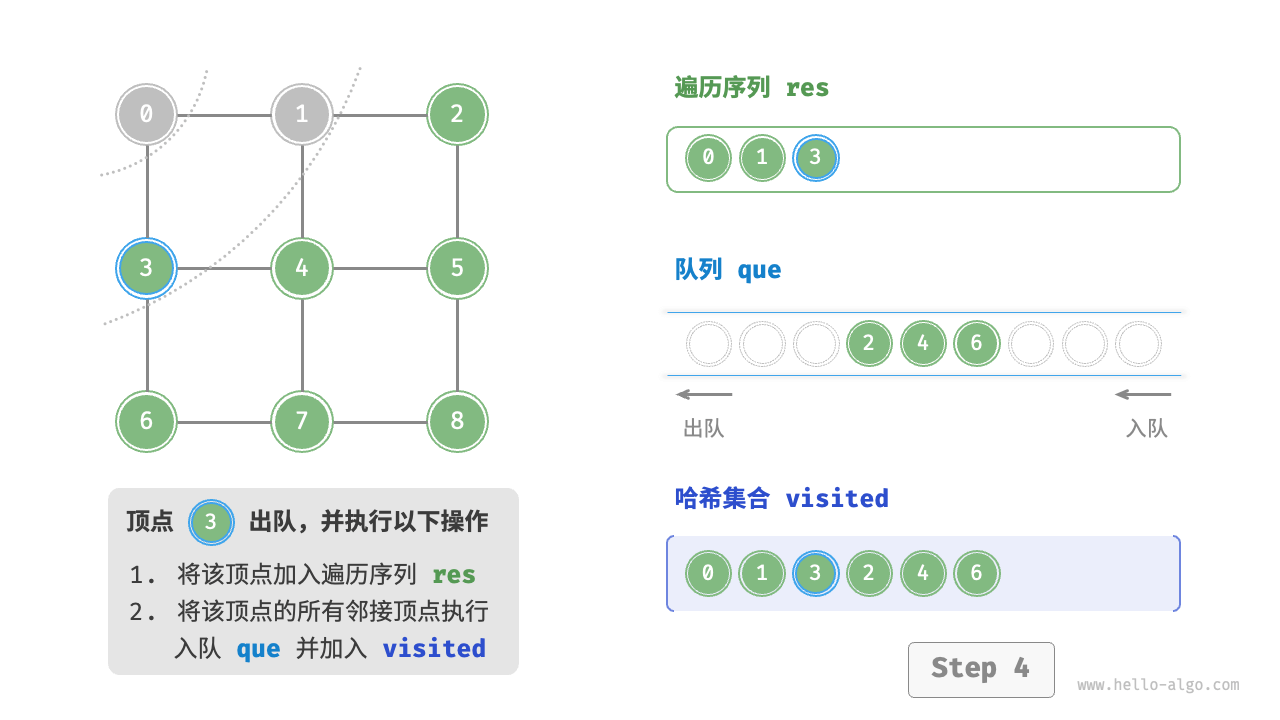
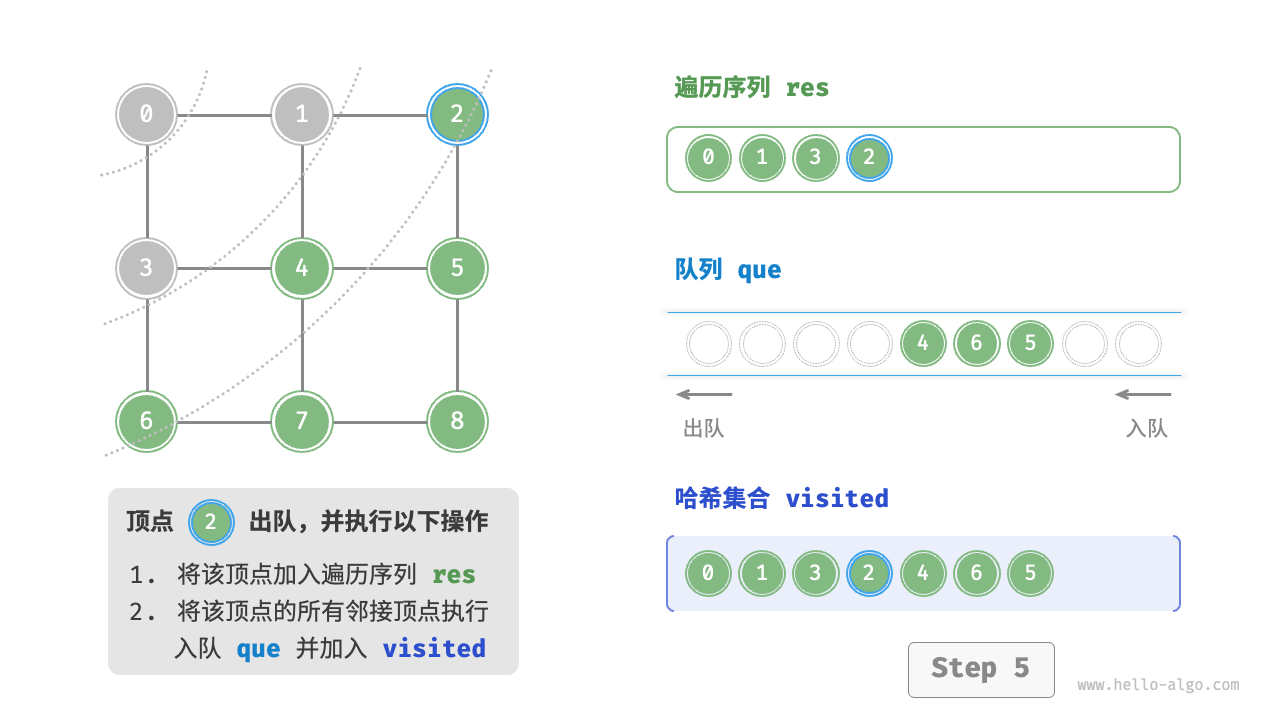
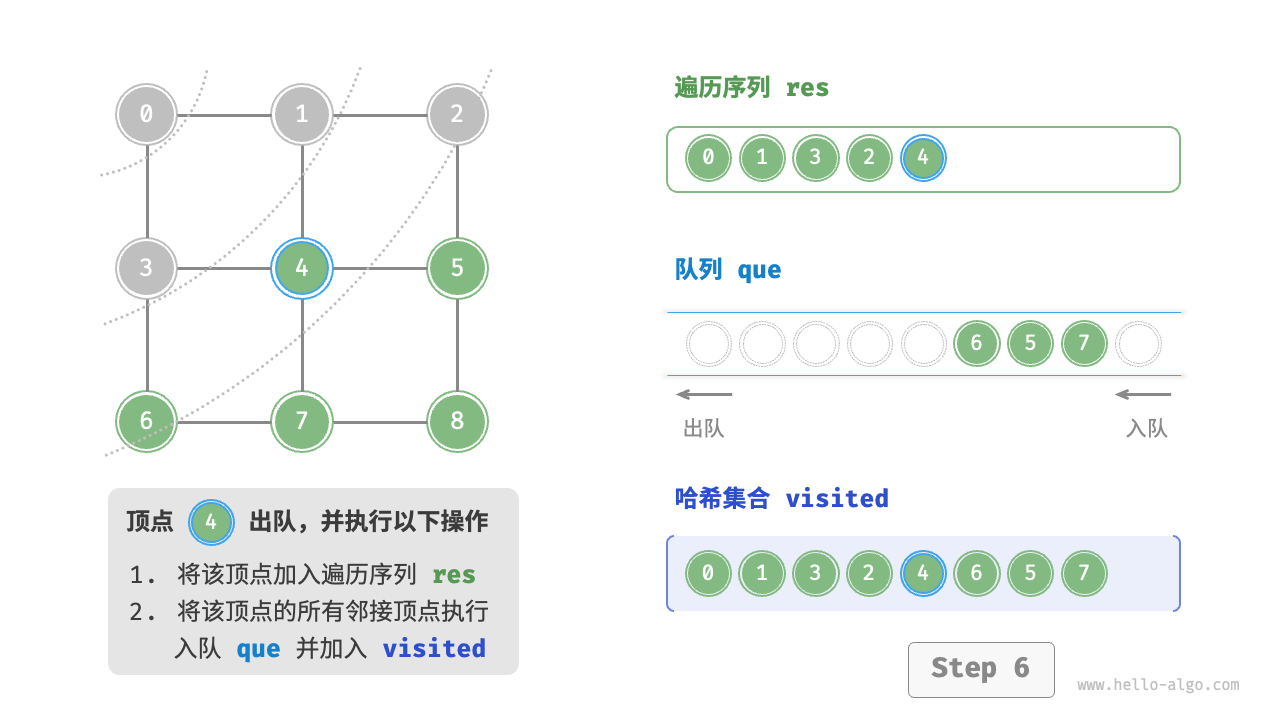
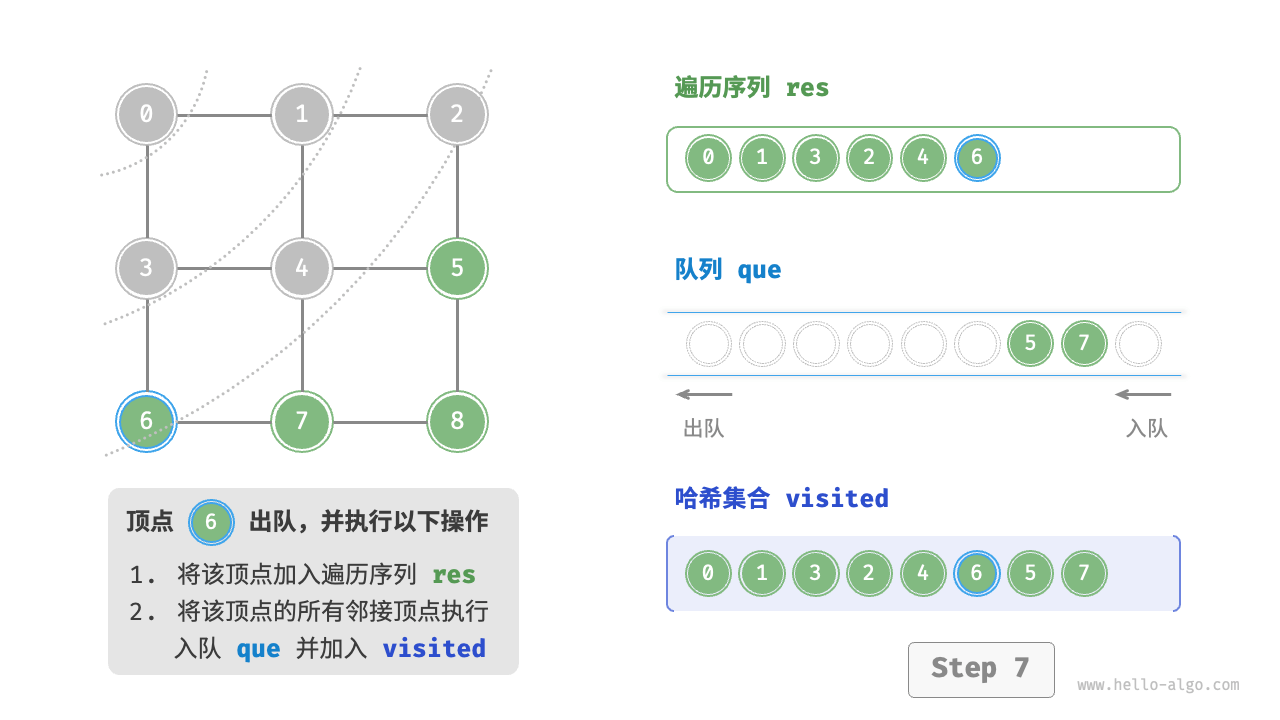
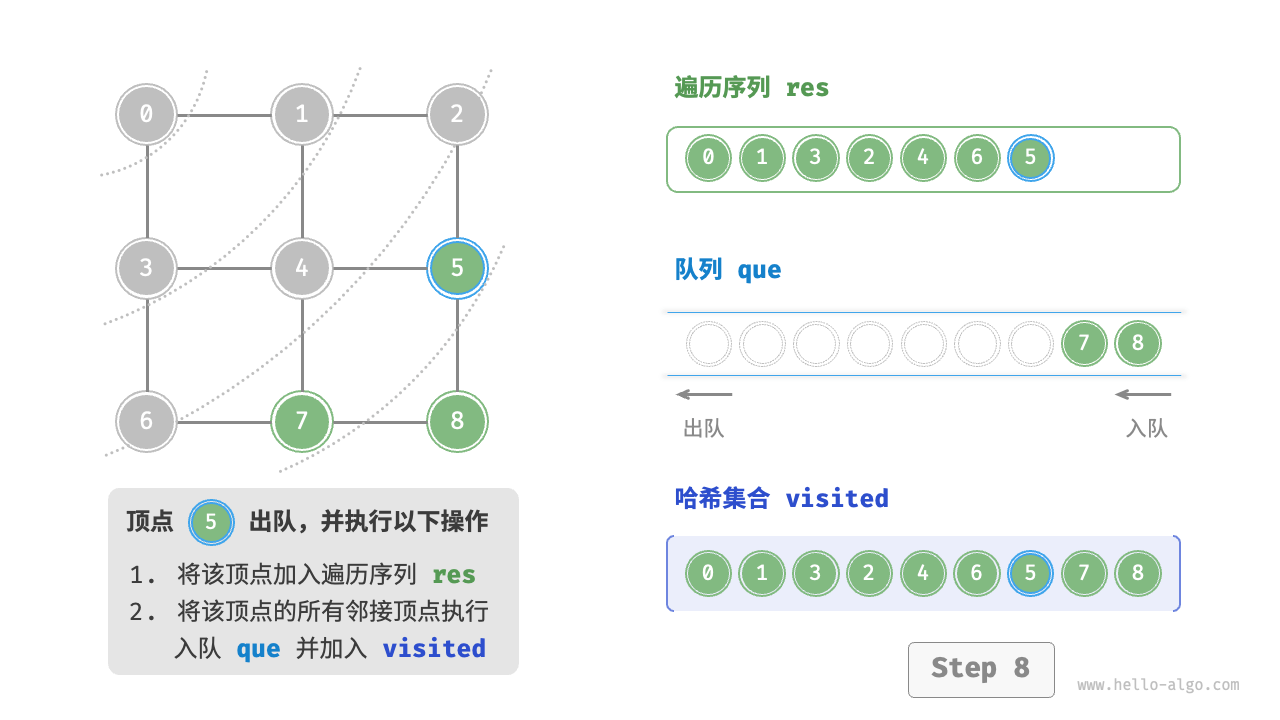
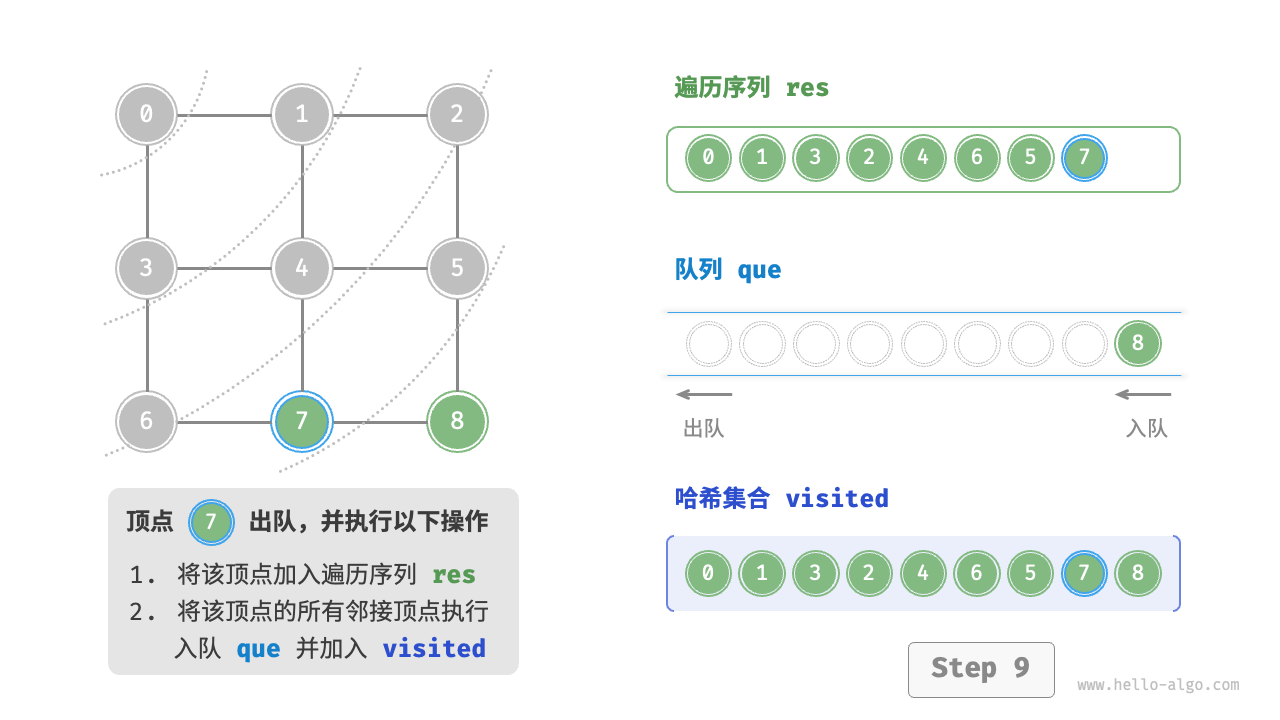
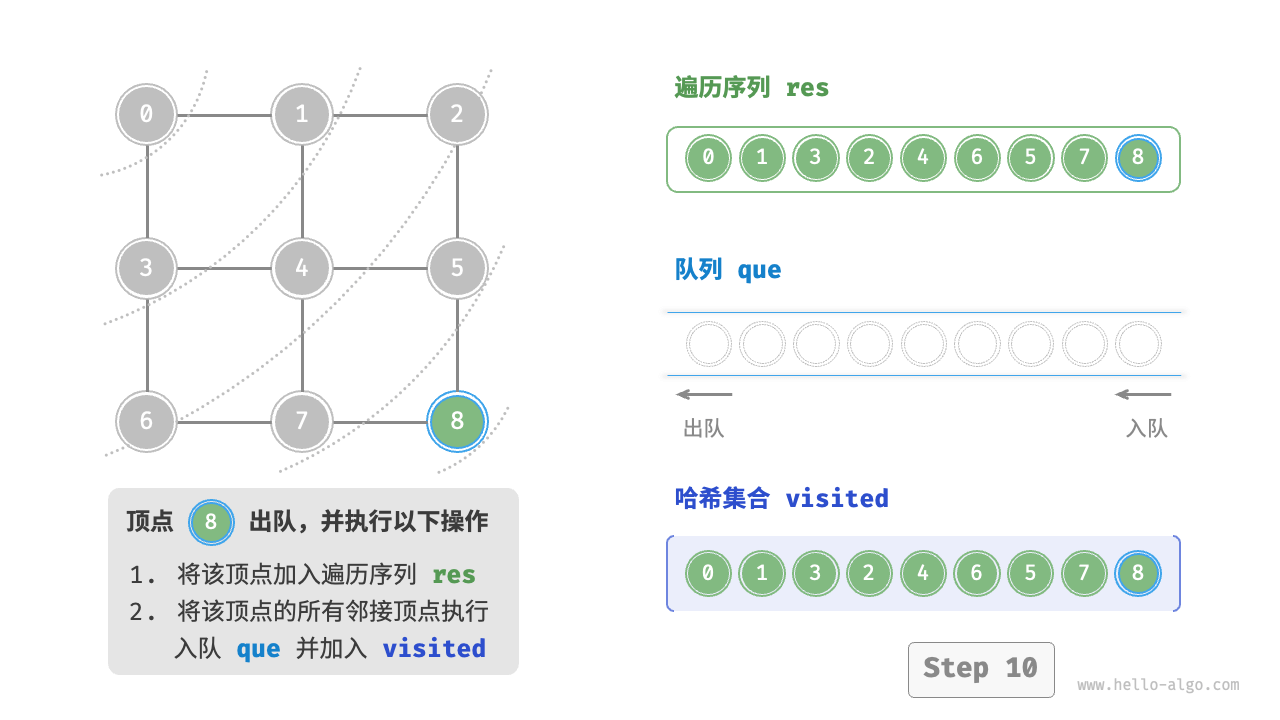
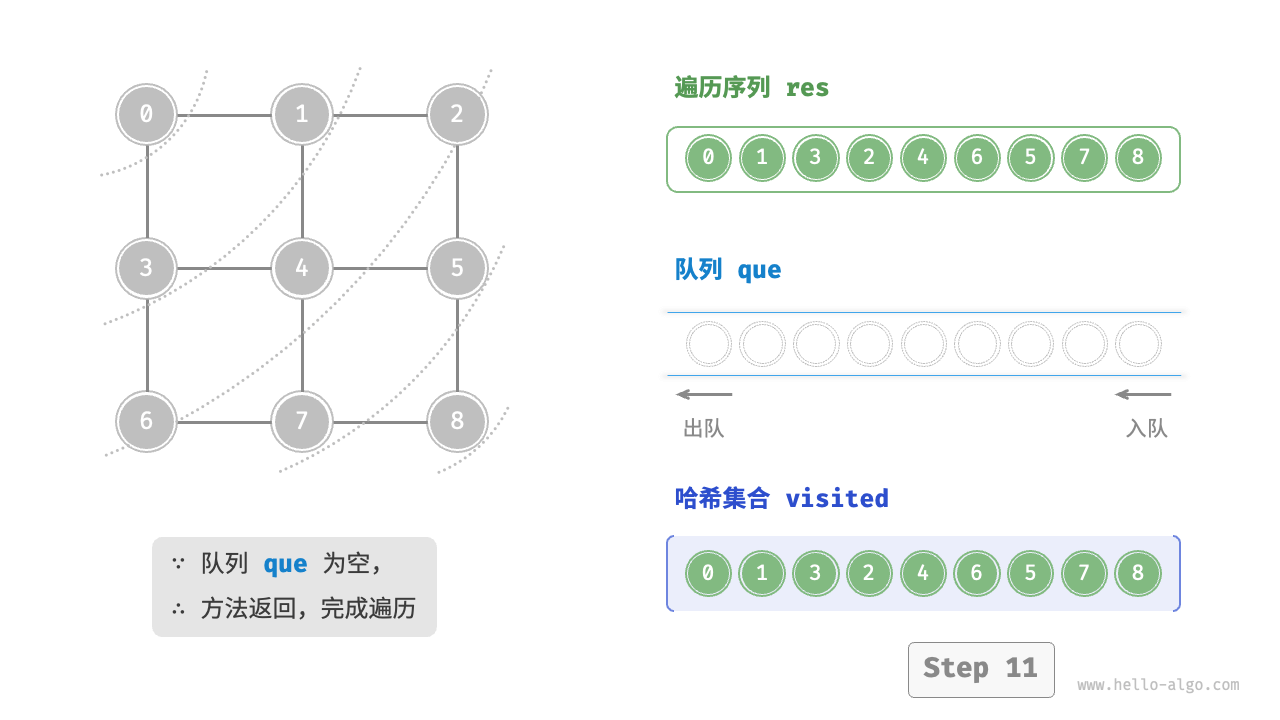
时间复杂度:所有顶点都会入队并出队一次,使用 $O(|V|)$ 时间;在遍历邻接顶点的过程中,由于是无向图,因此所有边都会被访问 2 次,使用 $O(2|E|)$ 时间;总体使用 $O(|V|+|E|)$ 时间。
空间复杂度:列表 res ,哈希集合 visited ,队列 que 中的顶点数量最多为 |V| ,使用 $O(|V|)$空间
- *深度优先遍历
深度优先遍历是一种优先走到底、无路可走再回头的遍历方式。如下图所示,从左上角顶点出发,访问当前顶点的某个邻接顶点,直到走到尽头时返回,再继续走到尽头并返回,以此类推,直至所有顶点遍历完成
![]()
/* 深度优先遍历辅助函数 */
void DFS(GraphAdjList graph, HashSet<Vertex> visited, List<Vertex> res, Vertex vet) {
res.Add(vet); // 记录访问顶点
visited.Add(vet); // 标记该顶点已被访问
// 遍历该顶点的所有邻接顶点
foreach (Vertex adjVet in graph.adjList[vet]) {
if (visited.Contains(adjVet)) {
continue; // 跳过已被访问的顶点
}
// 递归访问邻接顶点
DFS(graph, visited, res, adjVet);
}
}
/* 深度优先遍历 */
// 使用邻接表来表示图,以便获取指定顶点的所有邻接顶点
List<Vertex> GraphDFS(GraphAdjList graph, Vertex startVet) {
// 顶点遍历序列
List<Vertex> res = [];
// 哈希集合,用于记录已被访问过的顶点
HashSet<Vertex> visited = [];
DFS(graph, visited, res, startVet);
return res;
}
图的深度优先遍历步骤
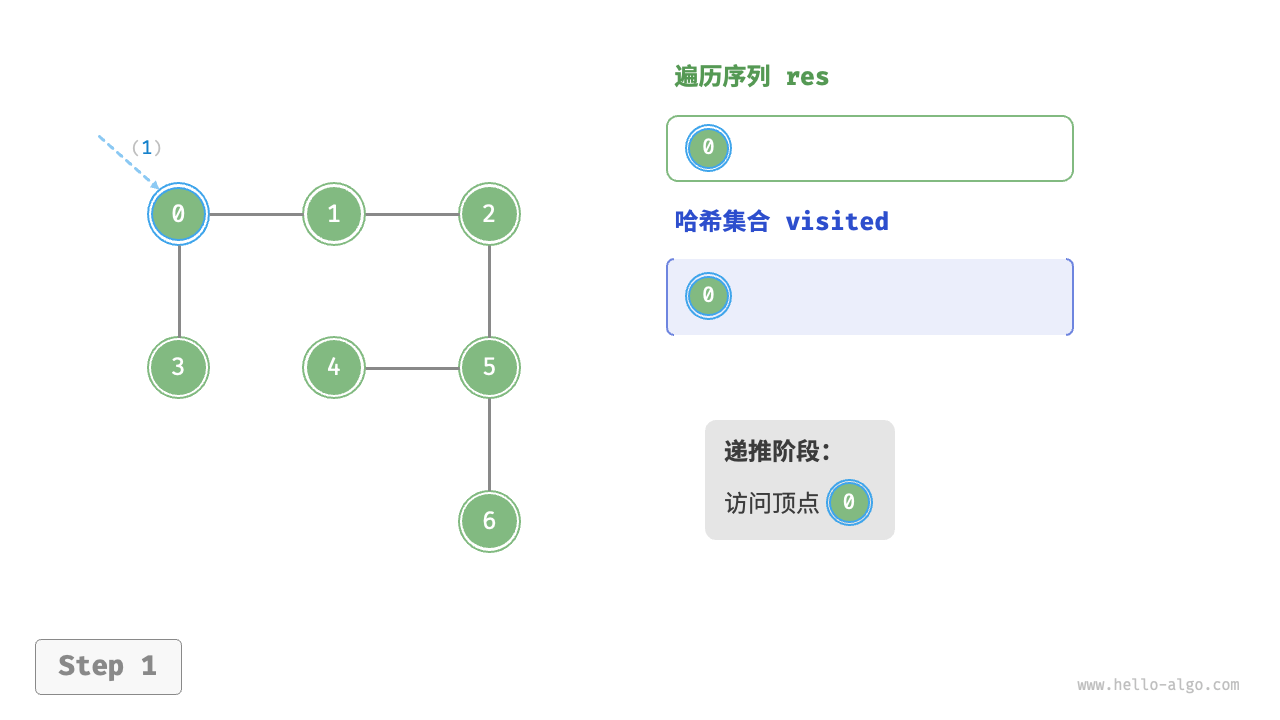
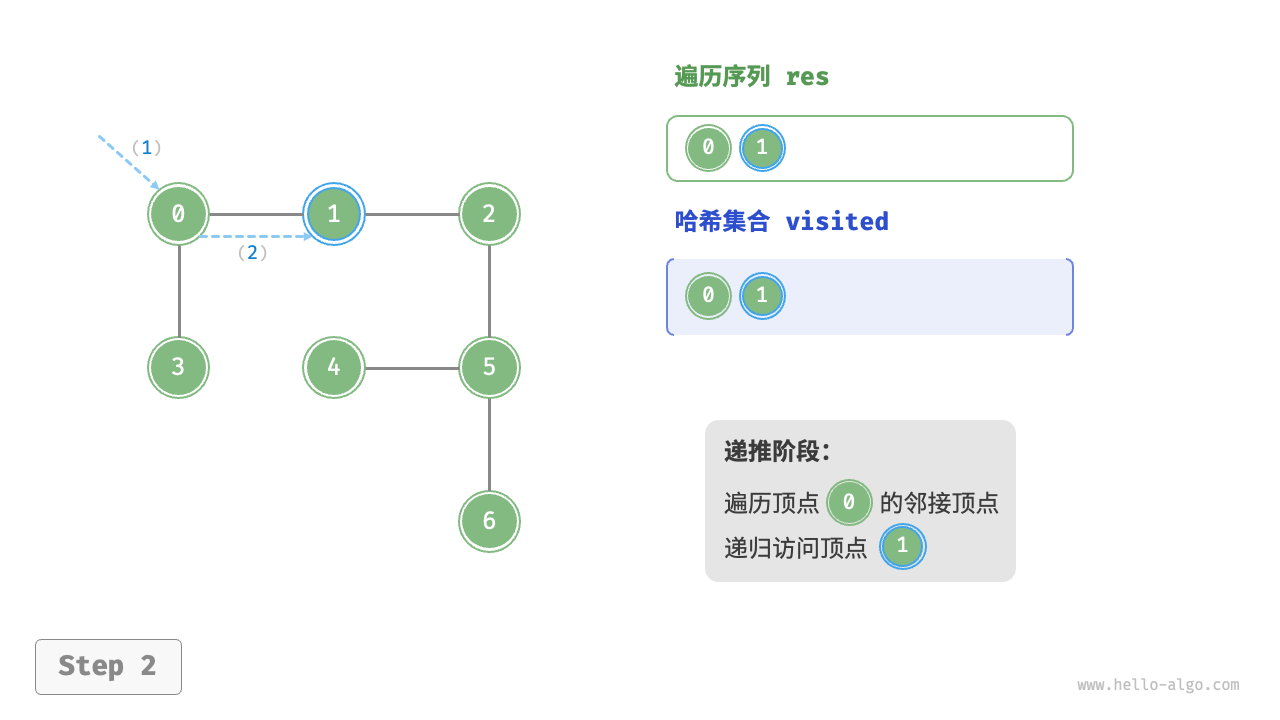
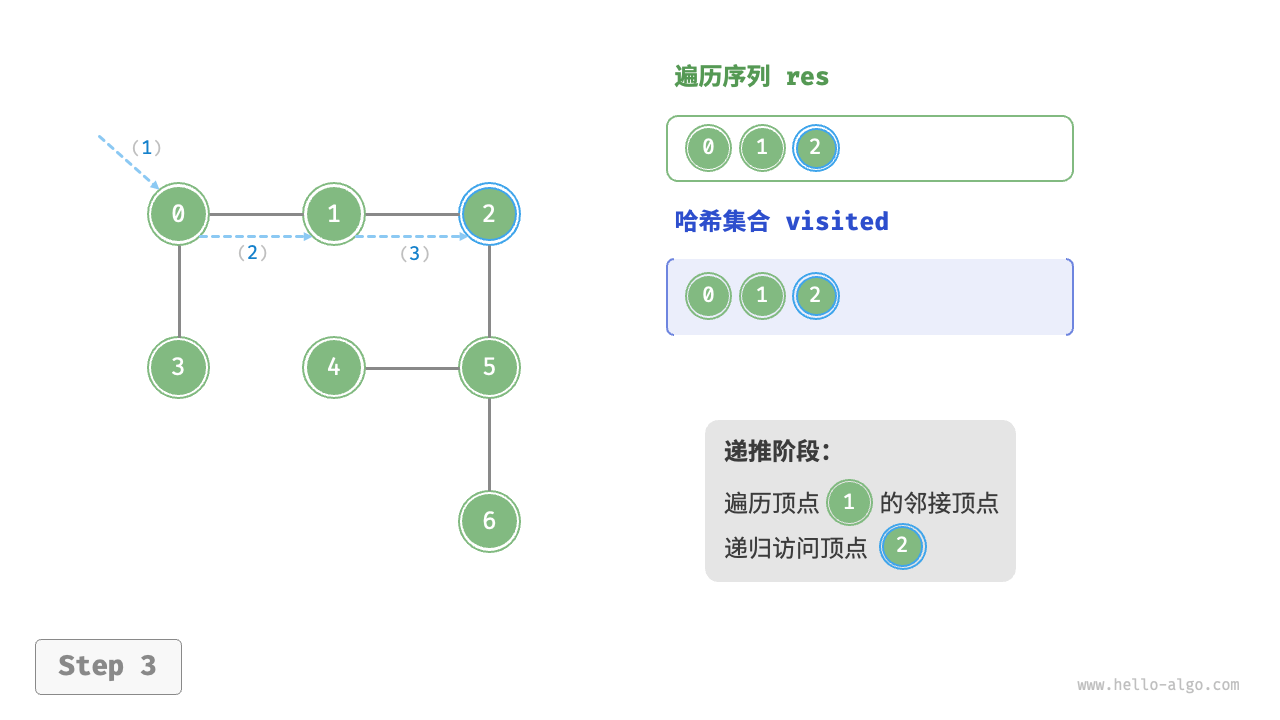
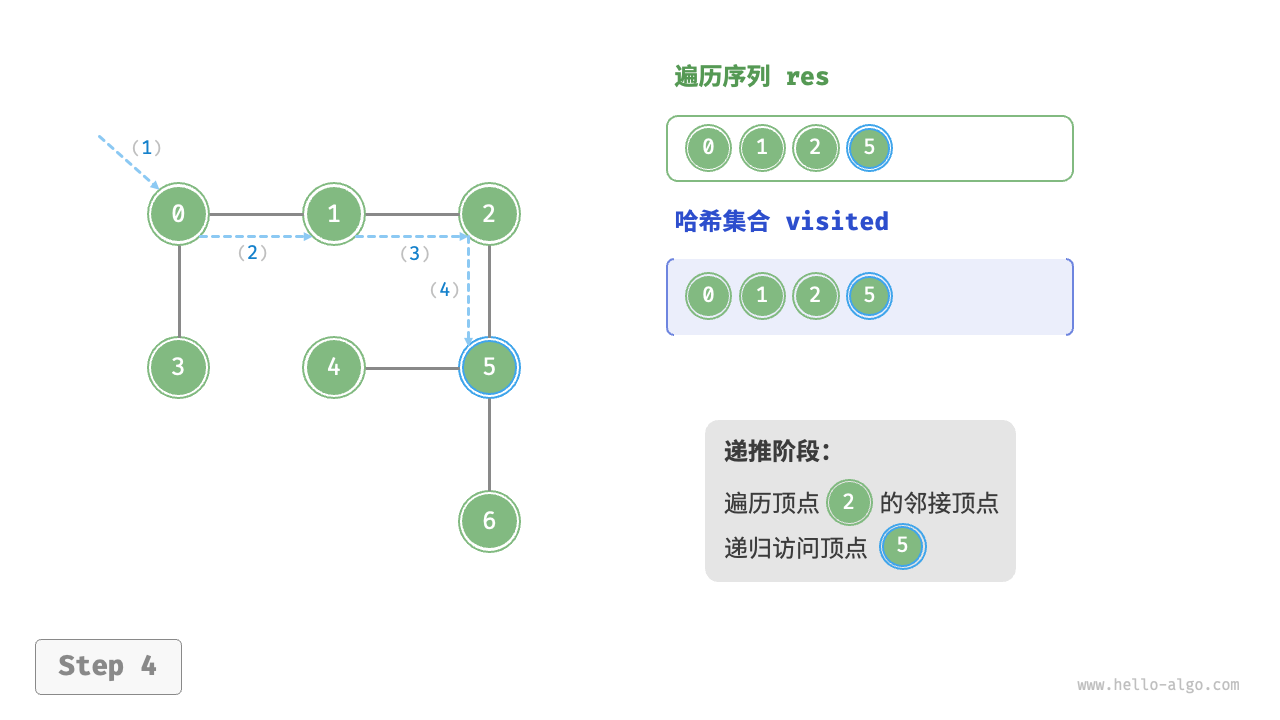
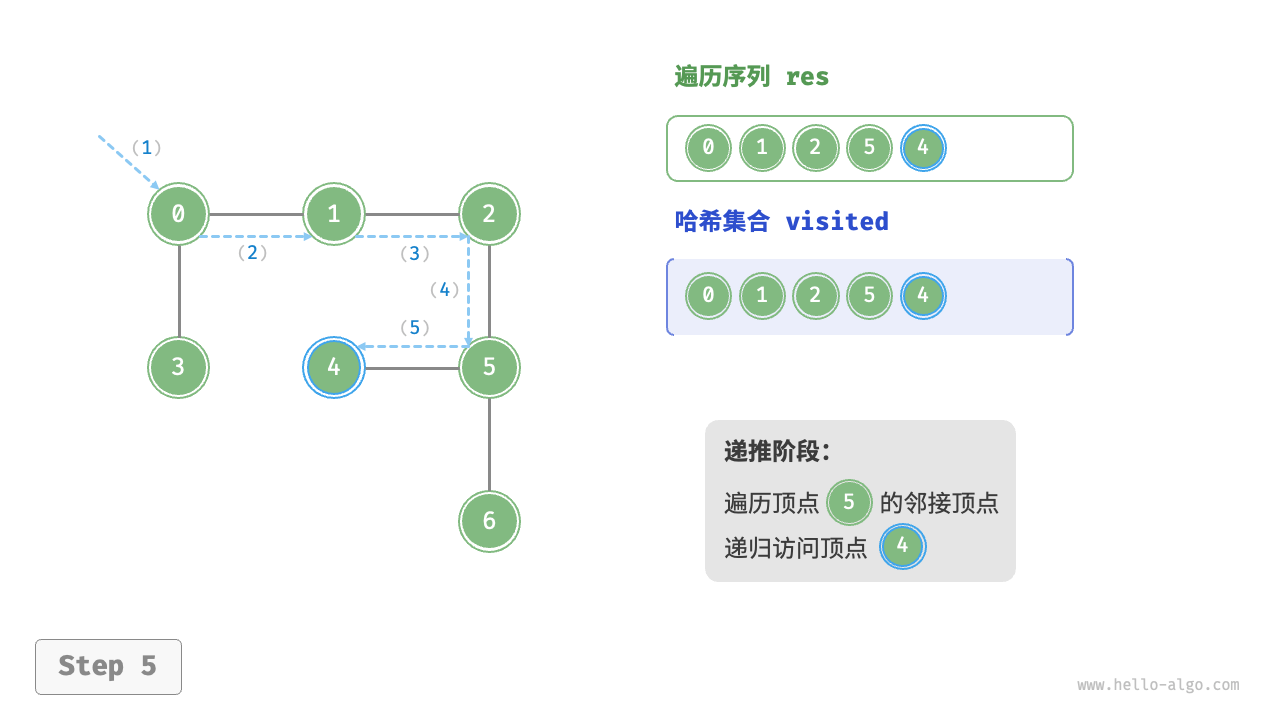
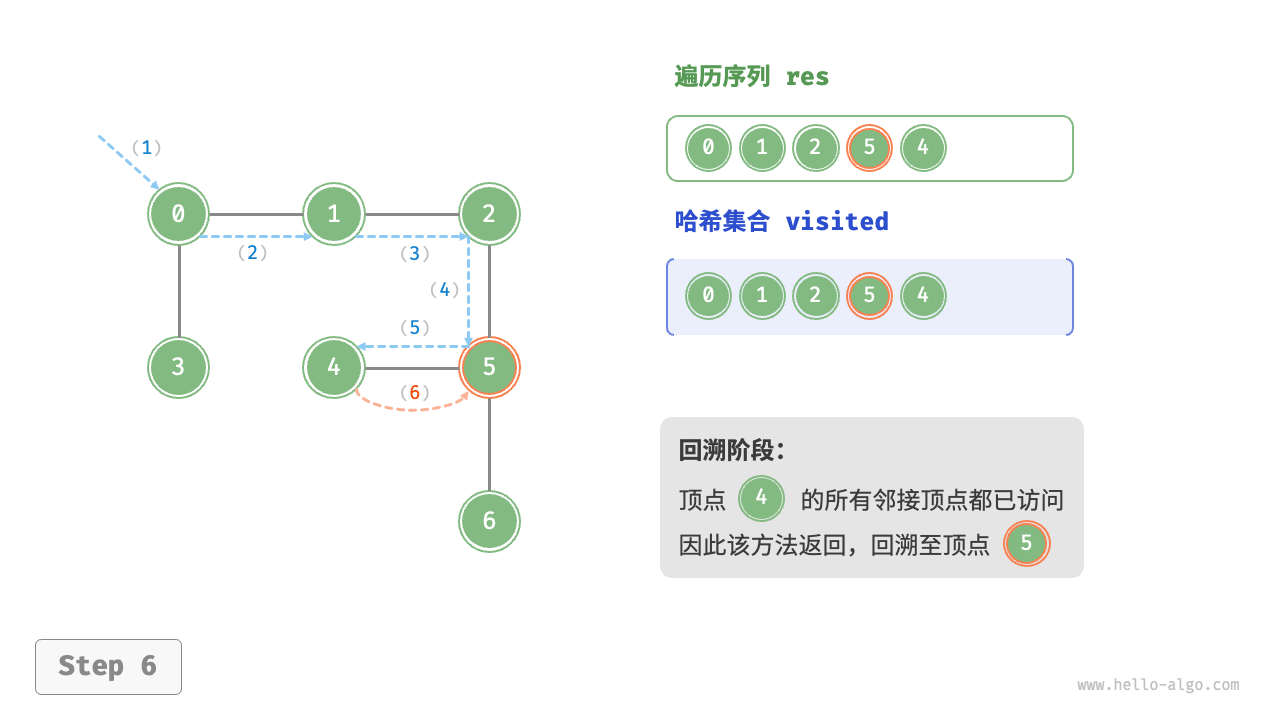
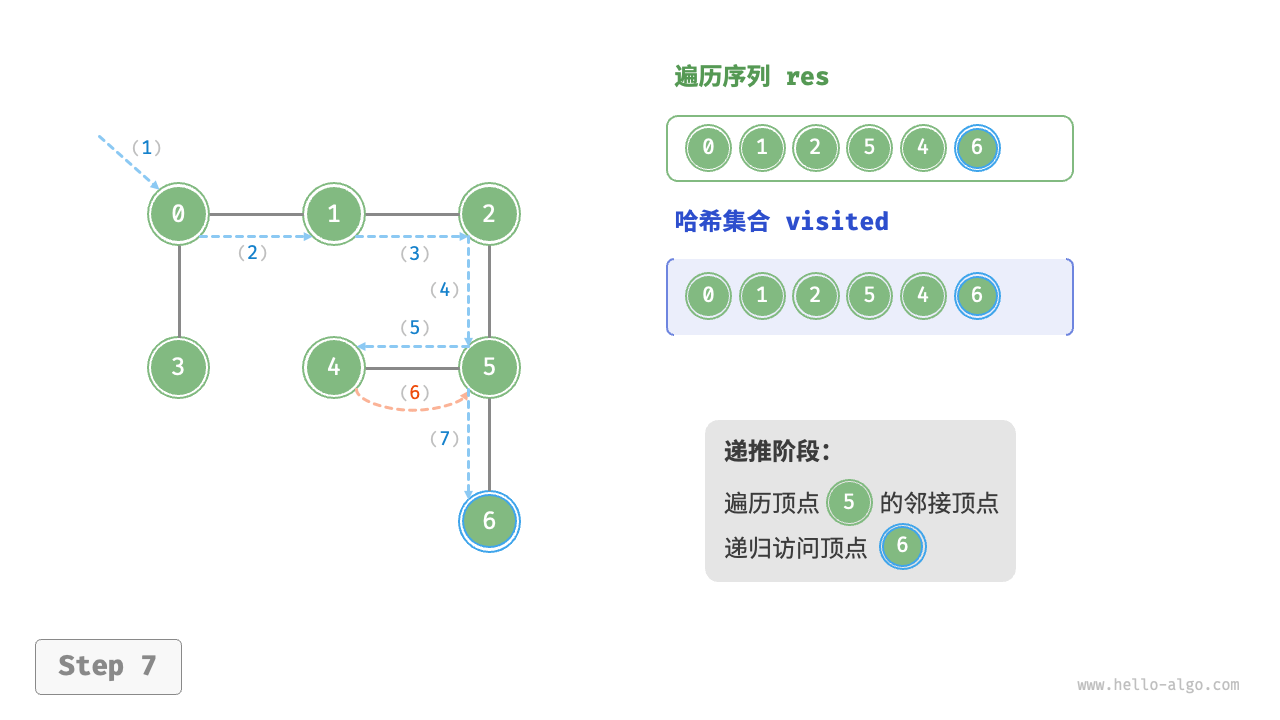
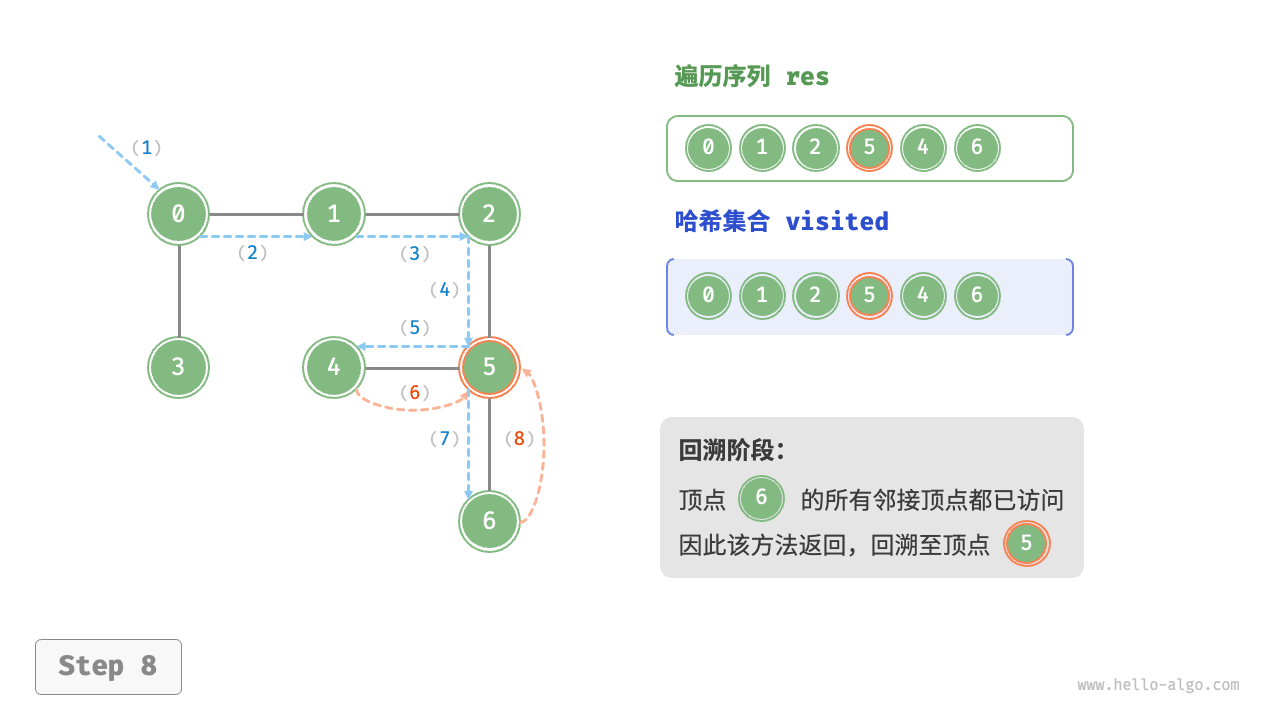
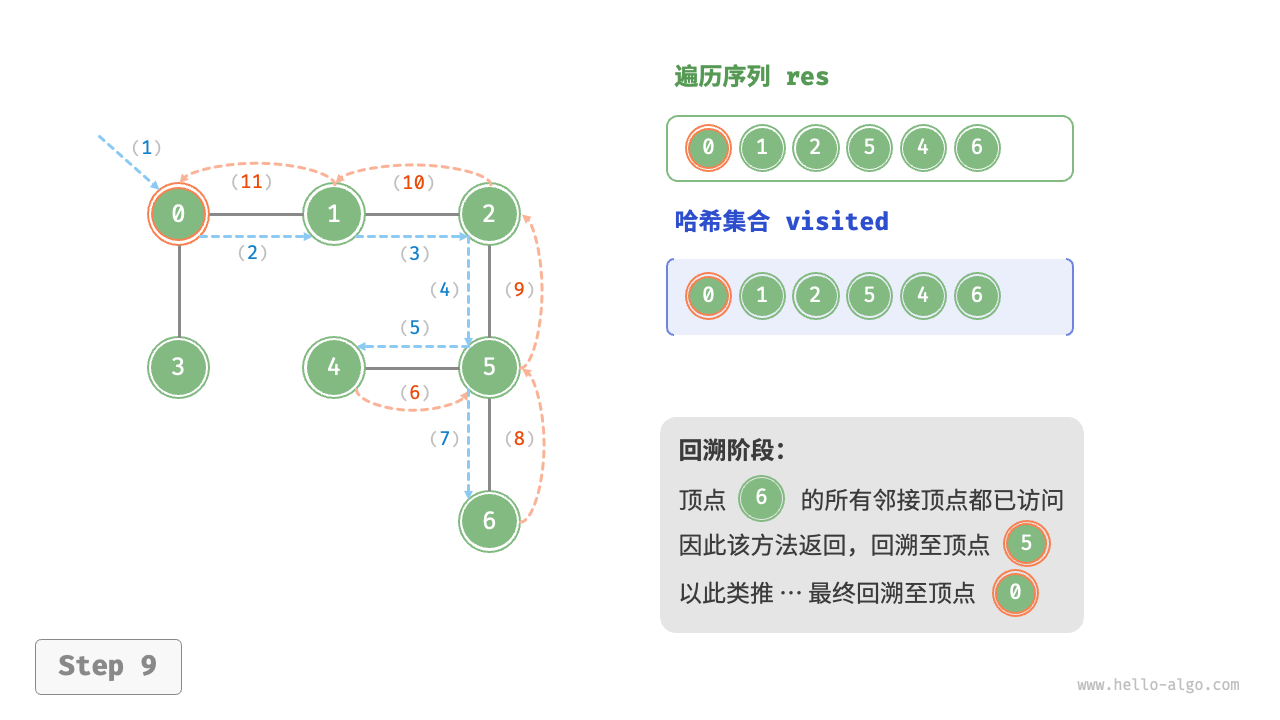
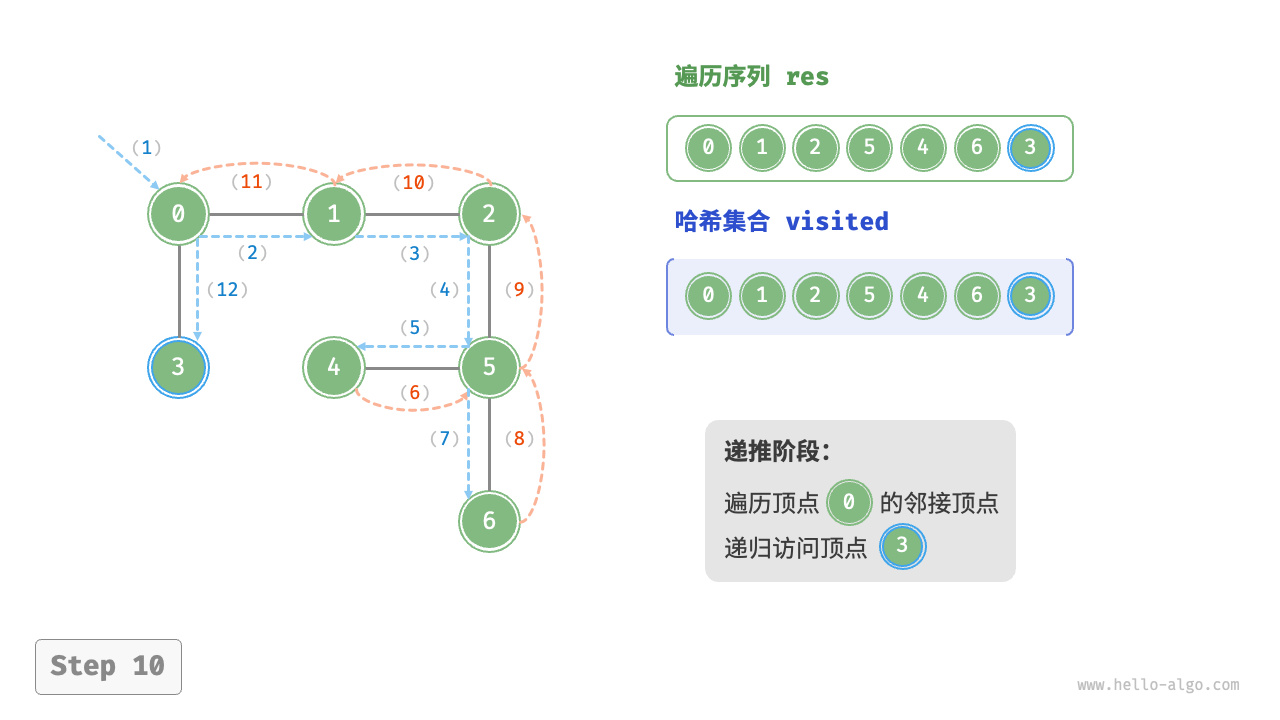
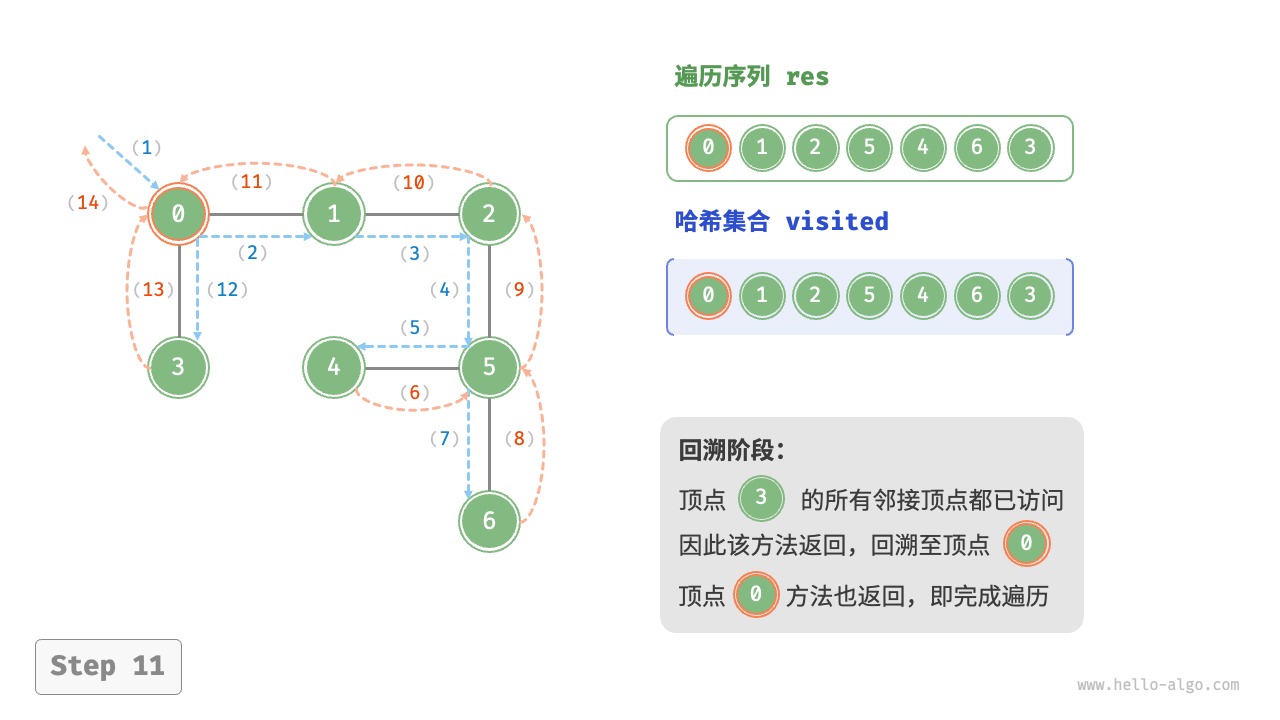
时间复杂度:所有顶点都会被访问 1 次,使用 $O(|V|)$ 时间;所有边都会被访问 2 次,使用 $O(2|E|)$时间;总体使用 $O(|V|+|E|)$ 时间。
空间复杂度:列表 res ,哈希集合 visited 顶点数量最多为 |V| ,递归深度最大为 |V| ,因此使用 $O(|V|)$ 空间
搜索
二分查找
二分查找(binary search)是一种氛围分治策略的高效搜索算法
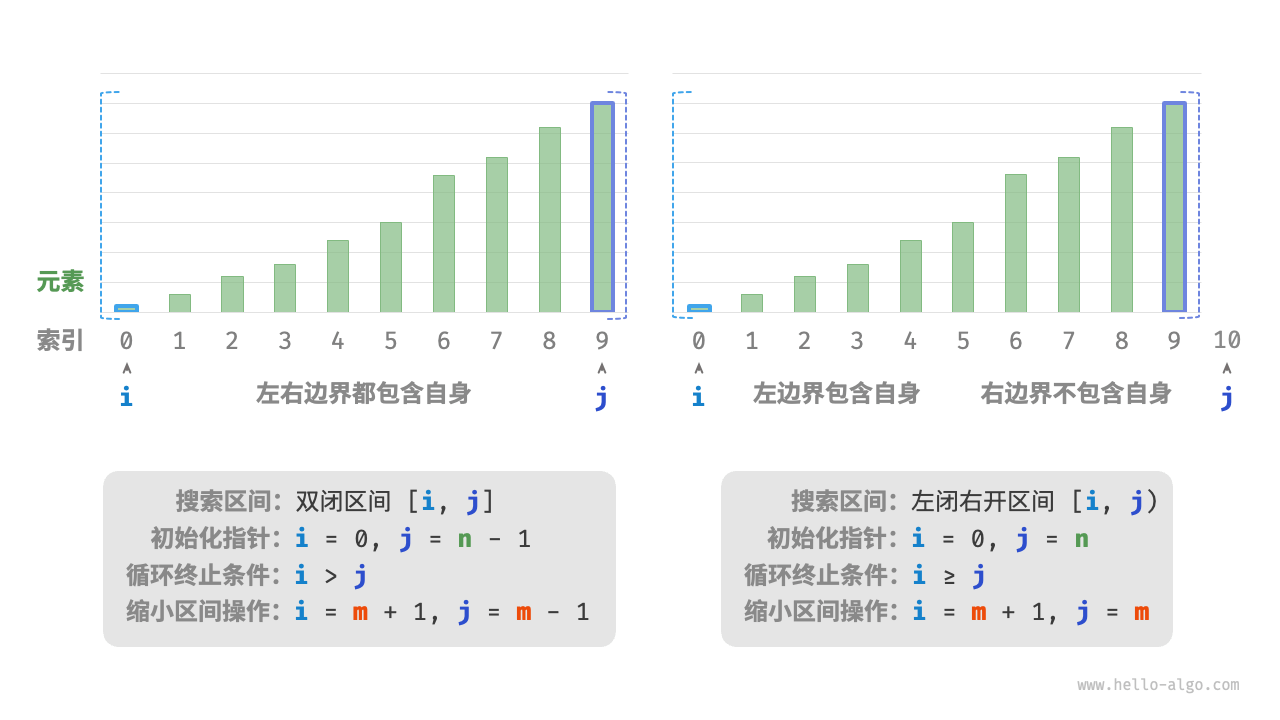
先初始化指针 i=0 和 j=n−1 ,分别指向数组首元素和尾元素,代表搜索区间 [0,n−1] 。请注意,中括号表示闭区间,其包含边界值本身。
接下来,循环执行以下两步:
- 计算中点索引
m=⌊(i+j)/2⌋,其中⌊⌋表示向下取整操作 - 判断
nums[m]和target的大小关系,分为以下三种情况- 当
nums[m] < target时,说明target在区间 [m+1,j] 中,因此执行 i=m+1 - 当
nums[m] > target时,说明target在区间 [i,m−1] 中,因此执行 j=m−1 - 当
nums[m] = target时,说明找到target,因此返回索引 m
若数组不包含目标元素,搜索区间最终会缩小为空。此时返回 −1
![]()
![]()
![]()
![]()
![]()
![]()
![]()
- 当
由于 i 和 j 都是 `int` 类型,**因此 i+j 可能会超出 `int` 类型的取值范围**。为了避免大数越界,我们通常采用公式 `m=⌊i+(j−i)/2⌋` 来计算中点
/* 二分查找(双闭区间) */
int BinarySearch(int[] nums, int target) {
// 初始化双闭区间 [0, n-1] ,即 i, j 分别指向数组首元素、尾元素
int i = 0, j = nums.Length - 1;
// 循环,当搜索区间为空时跳出(当 i > j 时为空)
while (i <= j) {
int m = i + (j - i) / 2; // 计算中点索引 m
if (nums[m] < target) // 此情况说明 target 在区间 [m+1, j] 中
i = m + 1;
else if (nums[m] > target) // 此情况说明 target 在区间 [i, m-1] 中
j = m - 1;
else // 找到目标元素,返回其索引
return m;
}
// 未找到目标元素,返回 -1
return -1;
}
时间复杂度为 O(logn) :在二分循环中,区间每轮缩小一半,因此循环次数为 $log_2n$
空间复杂度为 O(1) :指针 i 和 j 使用常数大小空间
常见的区间表示还有“左闭右开”区间,定义为 [0,n) ,即左边界包含自身,右边界不包含自身。在该表示下,区间 [i,j) 在 i=j 时为空
/* 二分查找(左闭右开区间) */
int BinarySearchLCRO(int[] nums, int target) {
// 初始化左闭右开区间 [0, n) ,即 i, j 分别指向数组首元素、尾元素+1
int i = 0, j = nums.Length;
// 循环,当搜索区间为空时跳出(当 i = j 时为空)
while (i < j) {
int m = i + (j - i) / 2; // 计算中点索引 m
if (nums[m] < target) // 此情况说明 target 在区间 [m+1, j) 中
i = m + 1;
else if (nums[m] > target) // 此情况说明 target 在区间 [i, m) 中
j = m;
else // 找到目标元素,返回其索引
return m;
}
// 未找到目标元素,返回 -1
return -1;
}
*二分查找在时间和空间方面都有较好的性能:
- 二分查找的时间效率高。在大数据量下,对数阶的时间复杂度具有显著优势。例如,当数据大小 $n=2^{20}$ 时,线性查找需要 $2^{20}=1048576$ 轮循环,而二分查找仅需 $log_22^{20}=20$ 轮循环。
- 二分查找无须额外空间。相较于需要借助额外空间的搜索算法(例如哈希查找),二分查找更加节省空间。
*二分查找并非适用于所有情况:
- 二分查找仅适用于有序数据。若输入数据无序,为了使用二分查找而专门进行排序,得不偿失。因为排序算法的时间复杂度通常为 $O(nlogn)$ ,比线性查找和二分查找都更高。对于频繁插入元素的场景,为保持数组有序性,需要将元素插入到特定位置,时间复杂度为 O(n) ,也是非常昂贵的。
- 二分查找仅适用于数组。二分查找需要跳跃式(非连续地)访问元素,而在链表中执行跳跃式访问的效率较低,因此不适合应用在链表或基于链表实现的数据结构。
- 小数据量下,线性查找性能更佳。在线性查找中,每轮只需 1 次判断操作;而在二分查找中,需要 1 次加法、1 次除法、1 ~ 3 次判断操作、1 次加法(减法),共 4 ~ 6 个单元操作;因此,当数据量 n 较小时,线性查找反而比二分查找更快
二分查找插入点
二分查找不仅可用于搜索目标元素,还可用于解决许多变种问题,比如搜索目标元素的插入位置
无重复元素的情况
给定一个长度为 n 的有序数组 `nums` 和一个元素 `target` ,数组不存在重复元素。现将 `target` 插入数组 `nums` 中,并保持其有序性。若数组中已存在元素 `target` ,则插入到其左方。请返回插入后 `target` 在数组中的索引
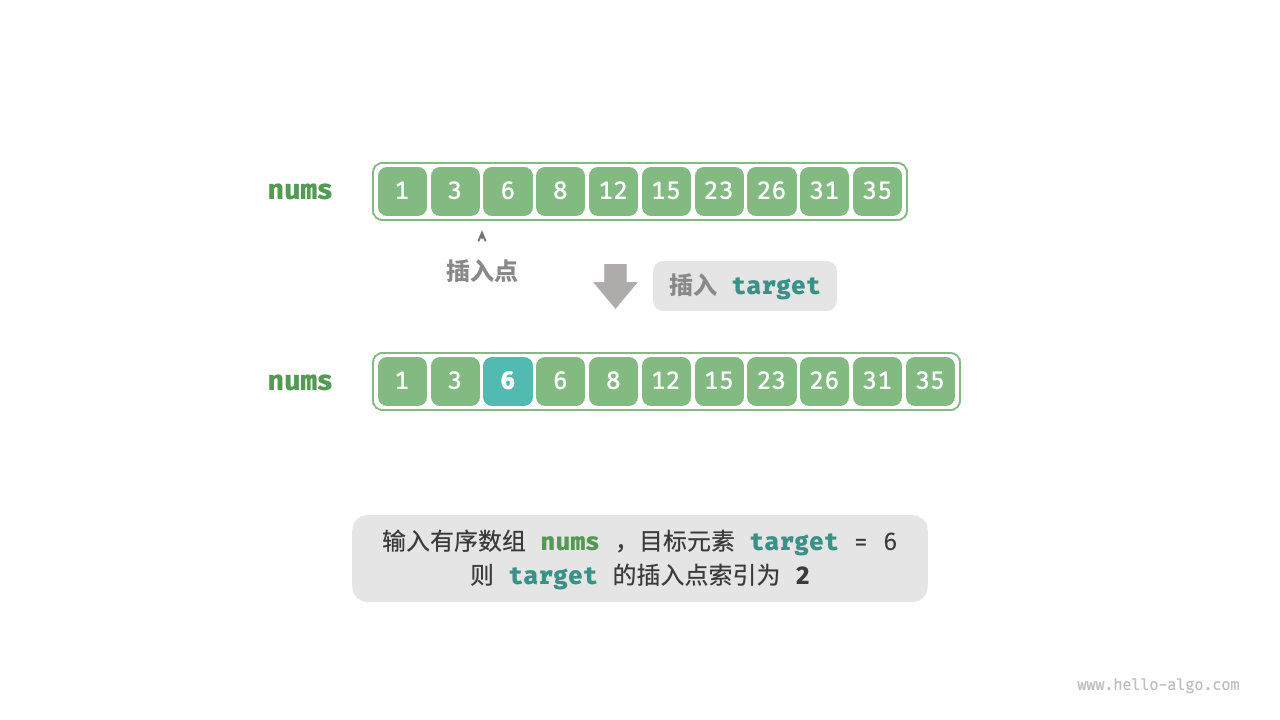
title:当数组中包含 `target` 时,插入点的索引是否是该元素的索引?
collapse:close
题目要求将 `target` 插入到相等元素的左边,这意味着新插入的 `target` 替换了原来 `target` 的位置。也就是说,**当数组包含 `target` 时,插入点的索引就是该 `target` 的索引**
title:当数组中不存在 `target` 时,插入点是哪个元素的索引?
collapse:close
进一步思考二分查找过程:当 `nums[m] < target` 时 i 移动,这意味着指针 i 在向大于等于 `target` 的元素靠近。同理,指针 j 始终在向小于等于 `target` 的元素靠近。
因此二分结束时一定有:i 指向首个大于 `target` 的元素,j 指向首个小于 `target` 的元素。**易得当数组不包含 `target` 时,插入索引为 i**
/* 二分查找插入点(无重复元素) */
int BinarySearchInsertionSimple(int[] nums, int target) {
int i = 0, j = nums.Length - 1; // 初始化双闭区间 [0, n-1]
while (i <= j) {
int m = i + (j - i) / 2; // 计算中点索引 m
if (nums[m] < target) {
i = m + 1; // target 在区间 [m+1, j] 中
} else if (nums[m] > target) {
j = m - 1; // target 在区间 [i, m-1] 中
} else {
return m; // 找到 target ,返回插入点 m
}
}
// 未找到 target ,返回插入点 i
return i;
}
有重复元素的情况
假设数组中存在多个 target ,则普通二分查找只能返回其中一个 target 的索引,而无法确定该元素的左边和右边还有多少 target
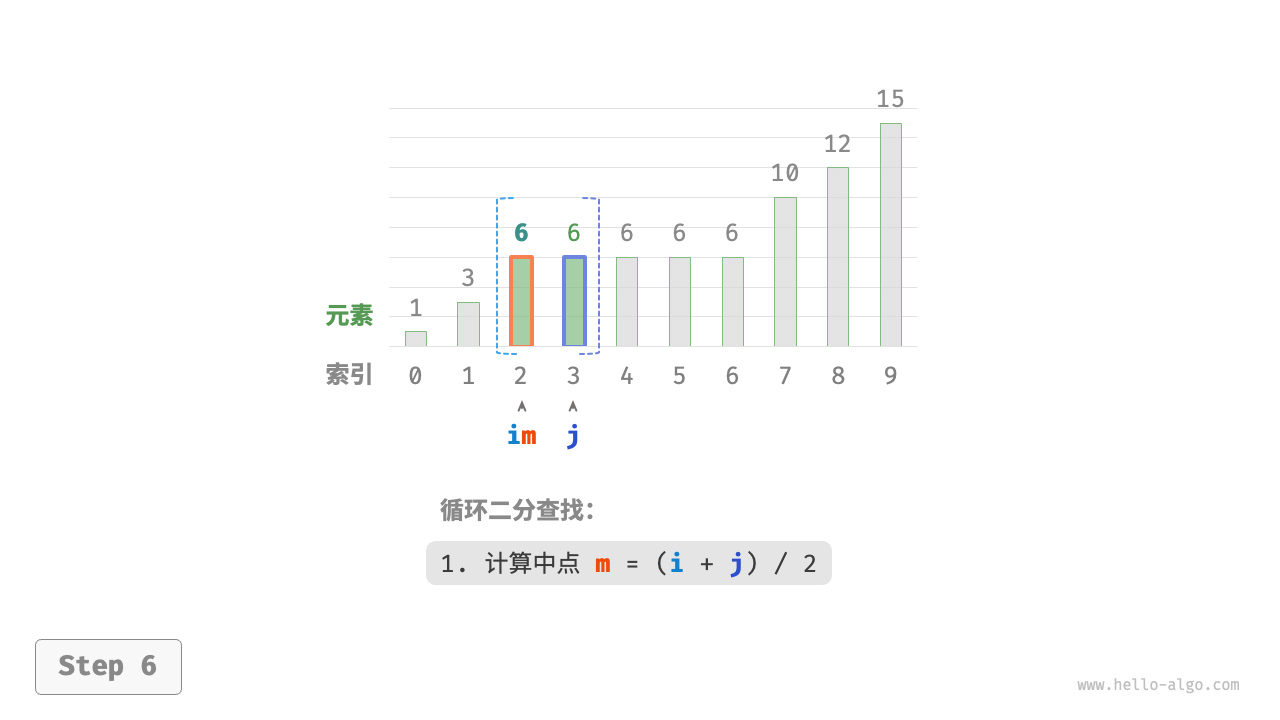
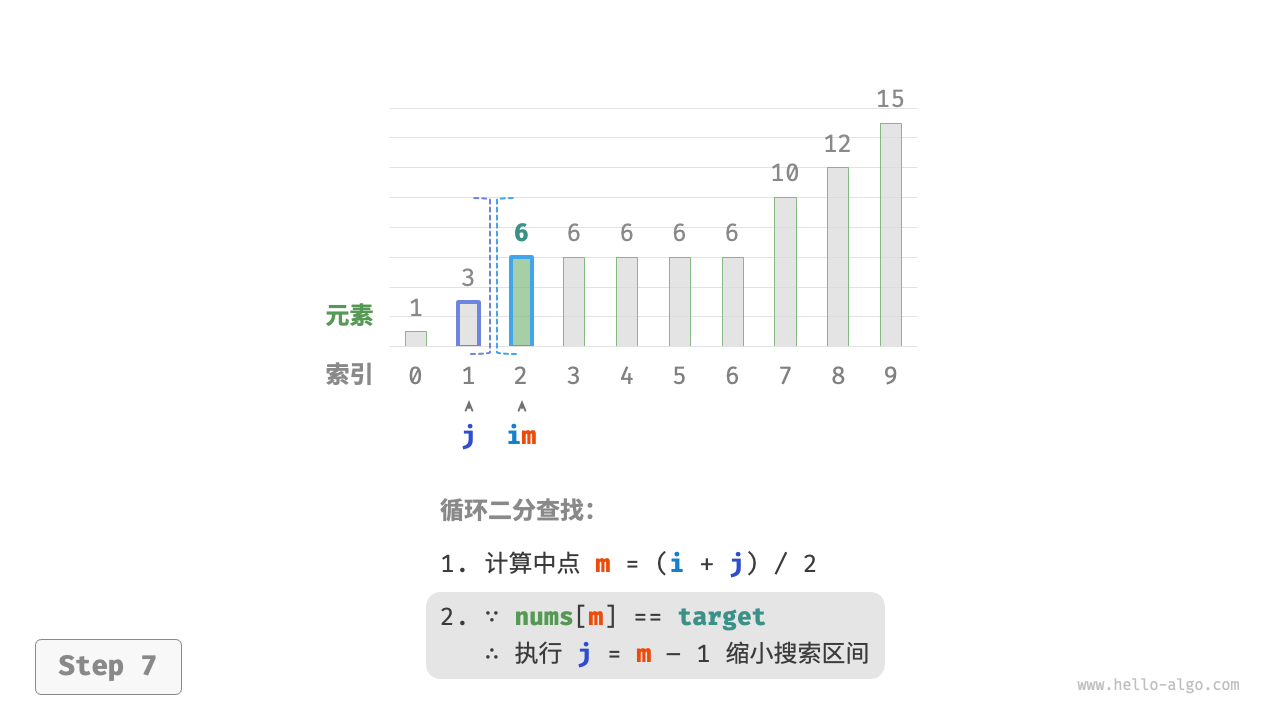
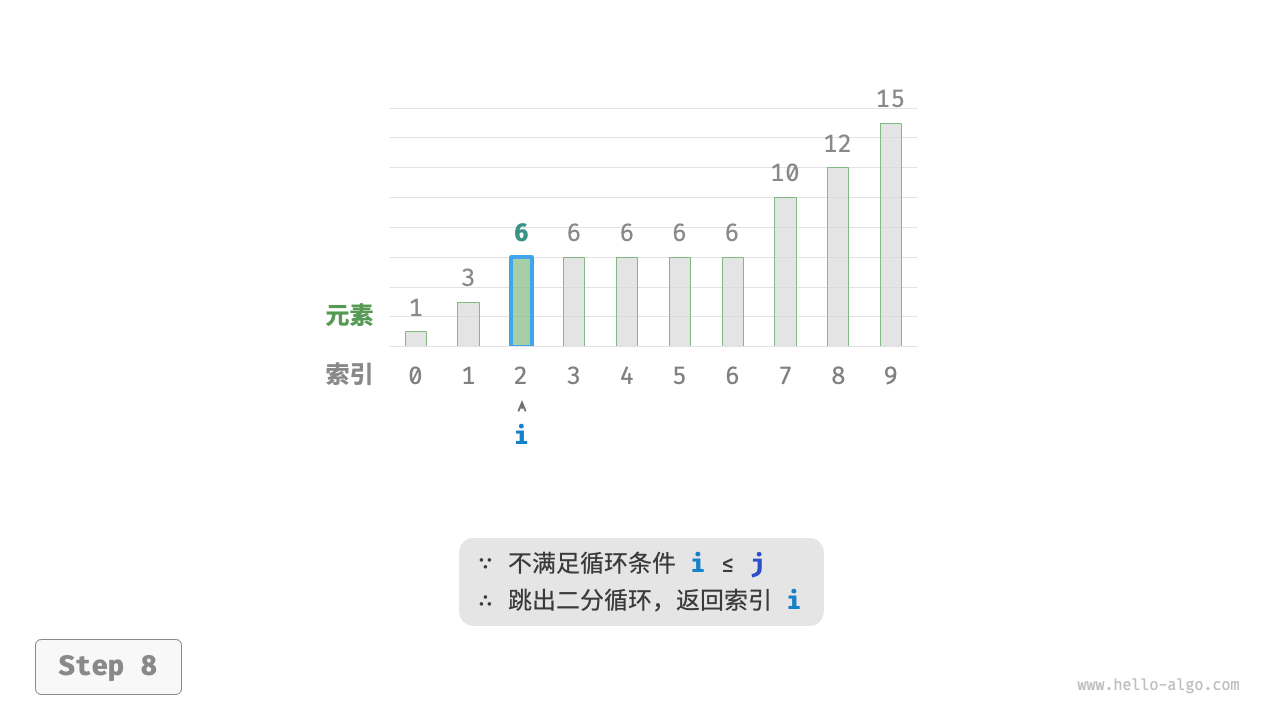
每轮先计算中点索引 m ,再判断 target 和 nums[m] 的大小关系,分为以下几种情况。
- 当
nums[m] < target或nums[m] > target时,说明还没有找到target,因此采用普通二分查找的缩小区间操作,从而使指针 i 和 j 向target靠近。 - 当
nums[m] == target时,说明小于target的元素在区间 [i,m−1] 中,因此采用 j=m−1 来缩小区间,从而使指针 j 向小于target的元素靠近。
循环完成后,i 指向最左边的 target ,j 指向首个小于 target 的元素,因此索引 i 就是插入点
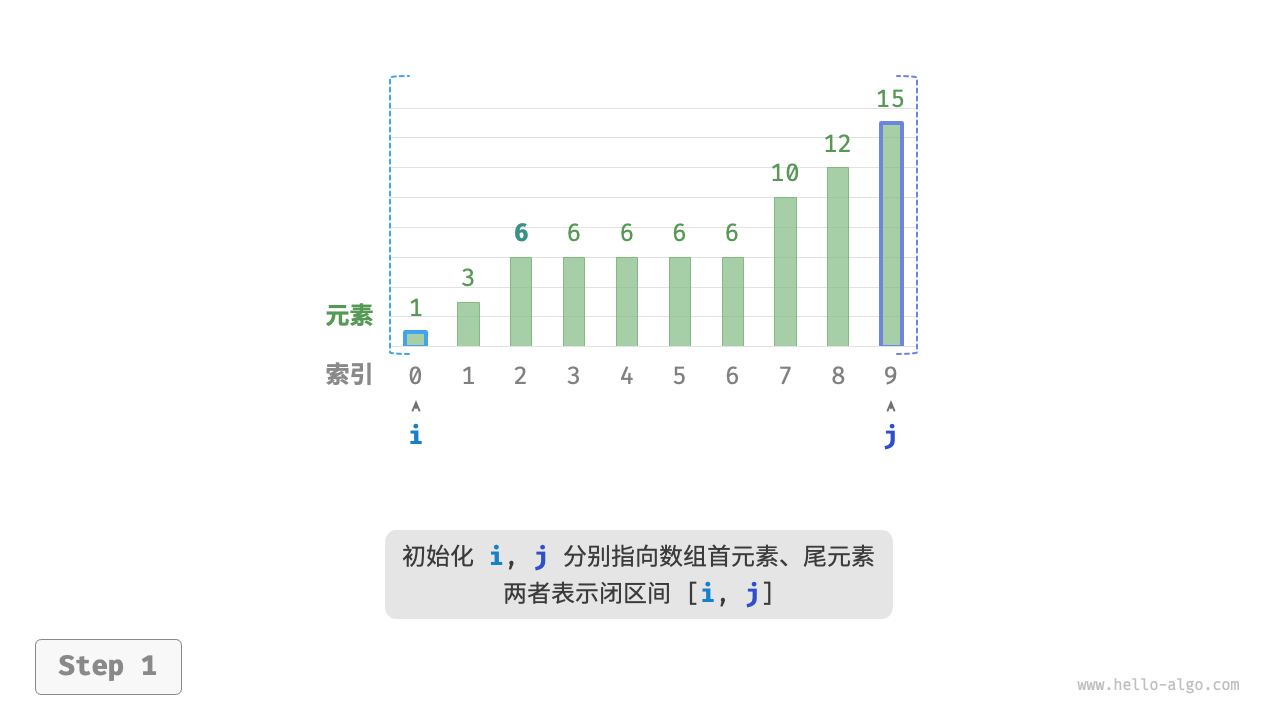
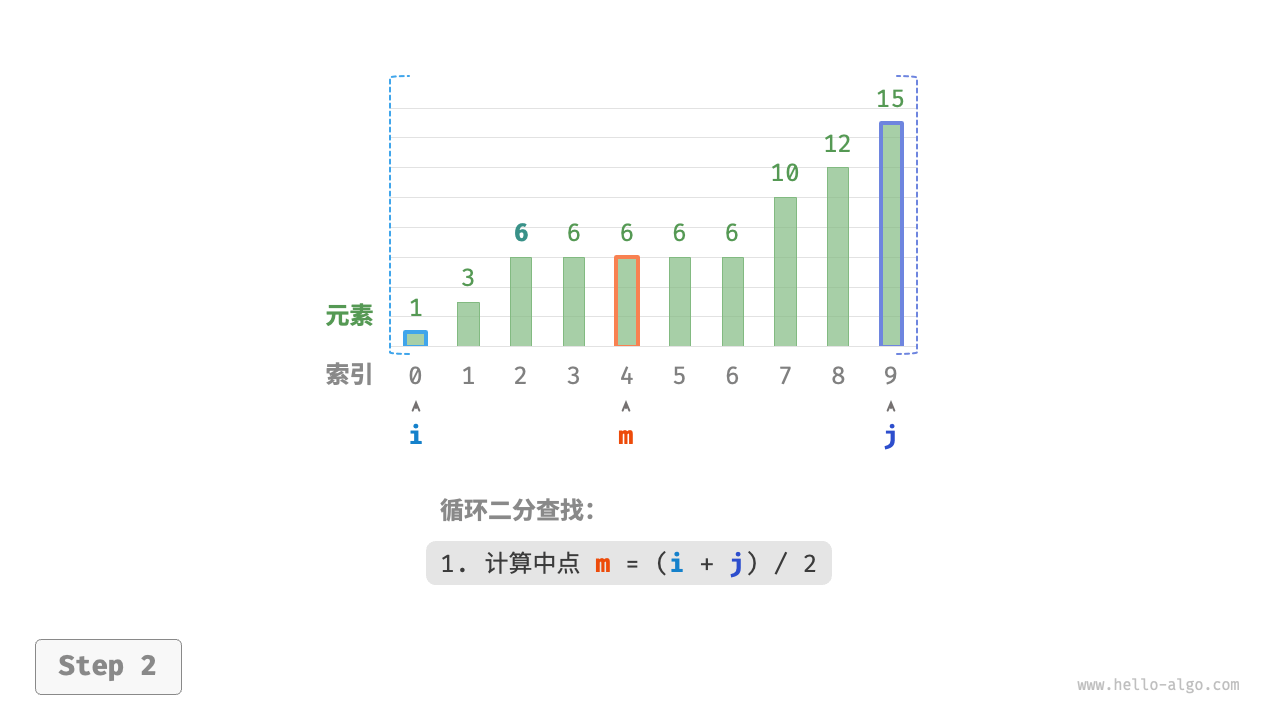
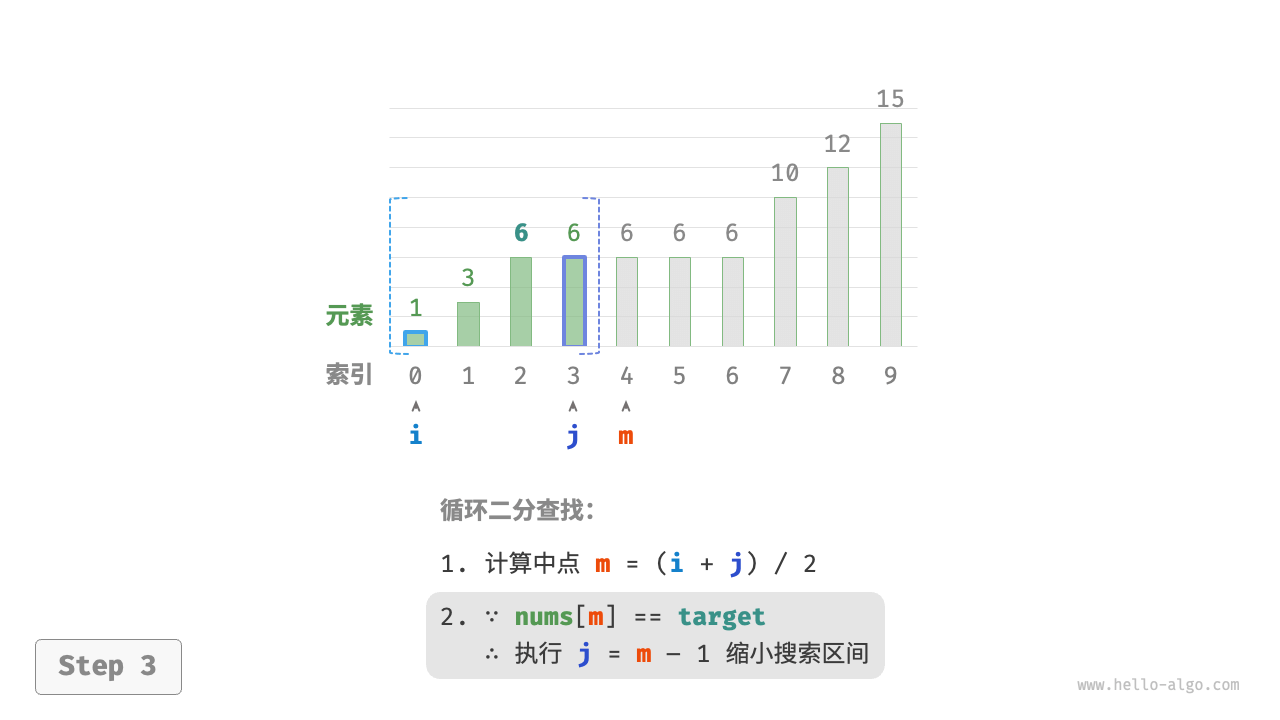
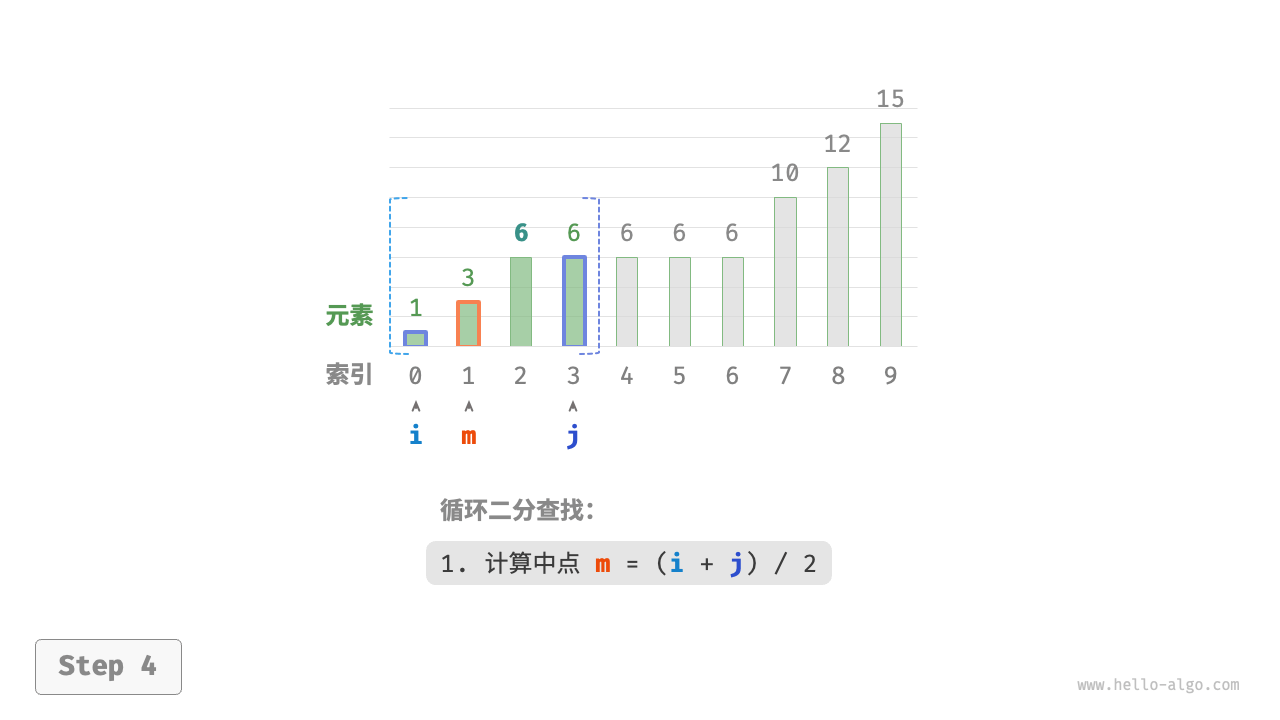
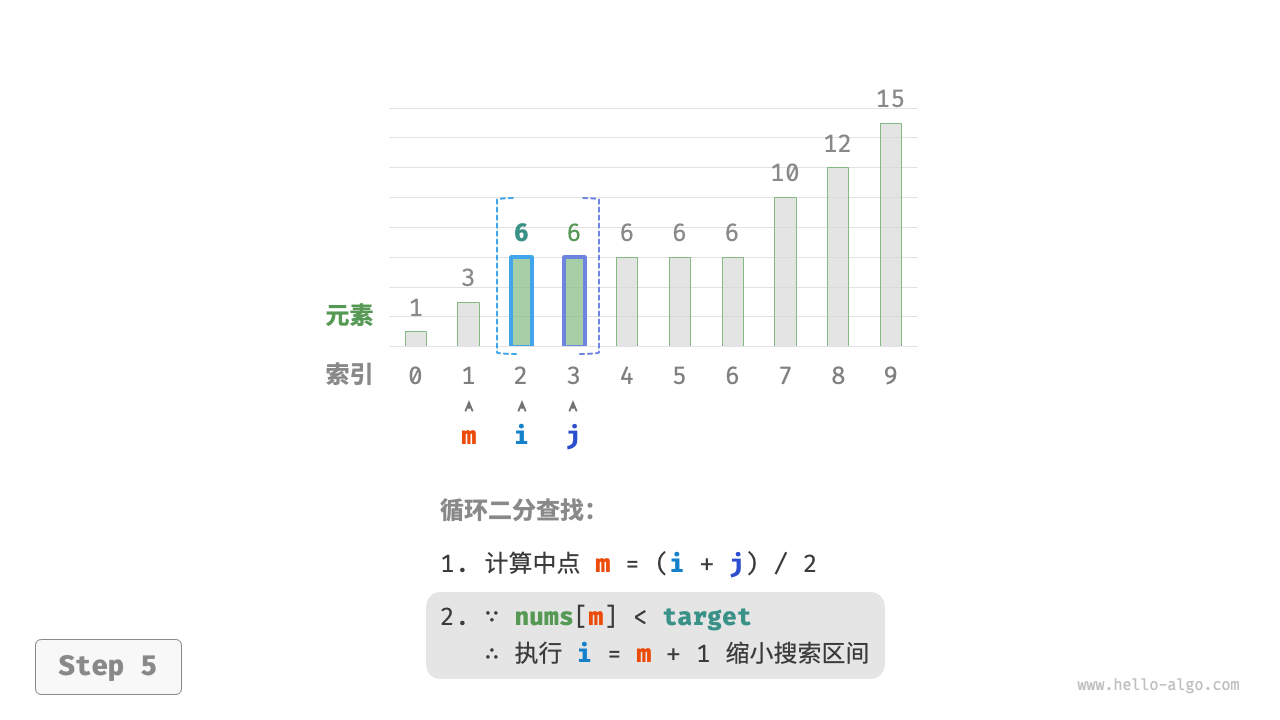
/* 二分查找插入点(存在重复元素) */
int BinarySearchInsertion(int[] nums, int target) {
int i = 0, j = nums.Length - 1; // 初始化双闭区间 [0, n-1]
while (i <= j) {
int m = i + (j - i) / 2; // 计算中点索引 m
if (nums[m] < target) {
i = m + 1; // target 在区间 [m+1, j] 中
} else if (nums[m] > target) {
j = m - 1; // target 在区间 [i, m-1] 中
} else {
j = m - 1; // 首个小于 target 的元素在区间 [i, m-1] 中
}
}
// 返回插入点 i
return i;
}
二分查找边界
查找左边界
给定一个长度为 n 的有序数组 `nums` ,其中可能包含重复元素。请返回数组中最左一个元素 `target` 的索引。若数组中不包含该元素,则返回 −1
回忆二分查找插入点的方法,搜索完成后 i 指向最左一个 target ,因此查找插入点本质上是在查找最左一个 target 的索引。
考虑通过查找插入点的函数实现查找左边界。请注意,数组中可能不包含 target ,这种情况可能导致以下两种结果。
- 插入点的索引 i 越界。
- 元素
nums[i]与target不相等。
当遇到以上两种情况时,直接返回 −1 即可
/* 二分查找最左一个 target */
int BinarySearchLeftEdge(int[] nums, int target) {
// 等价于查找 target 的插入点
int i = binary_search_insertion.BinarySearchInsertion(nums, target);
// 未找到 target ,返回 -1
if (i == nums.Length || nums[i] != target) {
return -1;
}
// 找到 target ,返回索引 i
return i;
}
查找右边界
可以利用查找最左元素的函数来查找最右元素,具体方法为:将查找最右一个 target 转化为查找最左一个 target + 1
查找完成后,指针 i 指向最左一个 target + 1(如果存在),而 j 指向最右一个 target ,因此返回 j 即可
注意,返回的插入点是 i ,因此需要将其减 1 ,从而获得 j :
/* 二分查找最右一个 target */
int BinarySearchRightEdge(int[] nums, int target) {
// 转化为查找最左一个 target + 1
int i = binary_search_insertion.BinarySearchInsertion(nums, target + 1);
// j 指向最右一个 target ,i 指向首个大于 target 的元素
int j = i - 1;
// 未找到 target ,返回 -1
if (j == -1 || nums[j] != target) {
return -1;
}
// 找到 target ,返回索引 j
return j;
}
哈希优化策略
给定一个整数数组 `nums` 和一个目标元素 `target` ,请在数组中搜索“和”为 `target` 的两个元素,并返回它们的数组索引。返回任意一个解即可。
/* 方法一:暴力枚举 */
int[] TwoSumBruteForce(int[] nums, int target) {
int size = nums.Length;
// 两层循环,时间复杂度为 O(n^2)
for (int i = 0; i < size - 1; i++) {
for (int j = i + 1; j < size; j++) {
if (nums[i] + nums[j] == target)
return [i, j];
}
}
return [];
}
时间复杂度为 $O(n^2)$ ,空间复杂度为 O(1)
/* 方法二:辅助哈希表 */
int[] TwoSumHashTable(int[] nums, int target) {
int size = nums.Length;
// 辅助哈希表,空间复杂度为 O(n)
Dictionary<int, int> dic = [];
// 单层循环,时间复杂度为 O(n)
for (int i = 0; i < size; i++) {
if (dic.ContainsKey(target - nums[i])) {
return [dic[target - nums[i]], i];
}
dic.Add(nums[i], i);
}
return [];
}
时间复杂度为O(n) ,空间复杂度为 O(n)
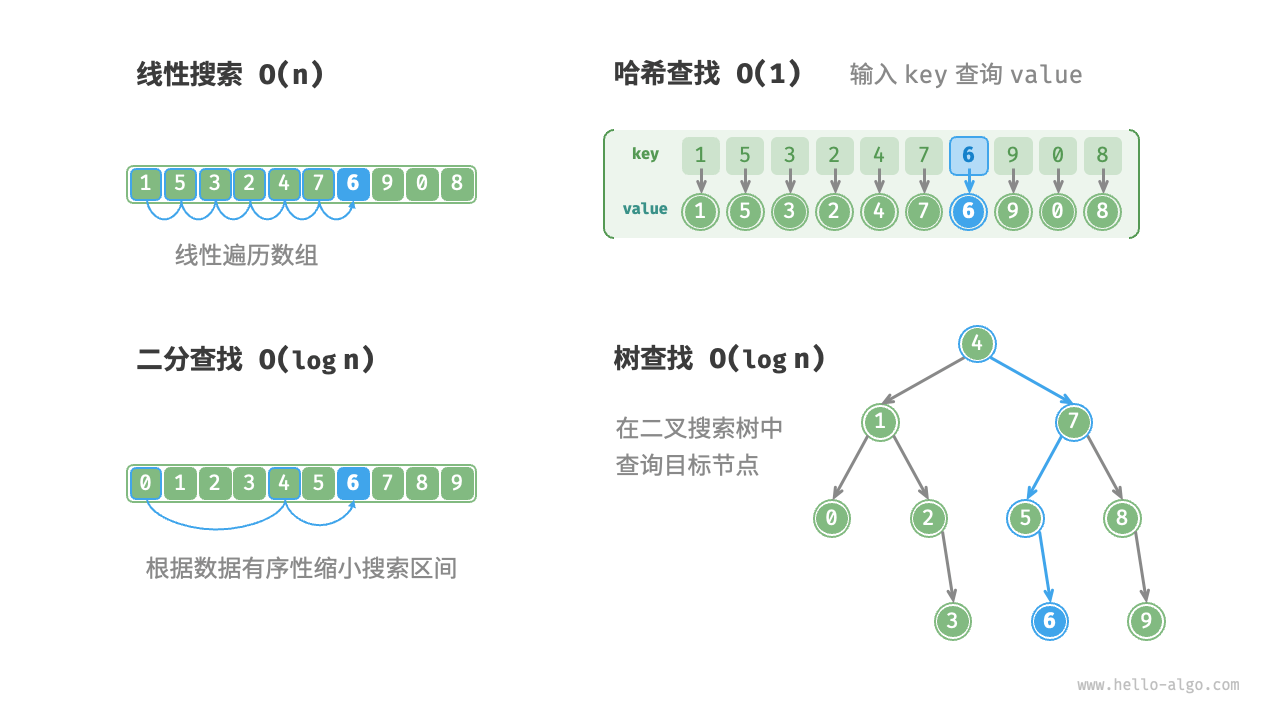
查找算法效率对比
| 线性搜索 | 二分查找 | 树查找 | 哈希查找 | |
|---|---|---|---|---|
| 查找元素 | ||||
| 插入元素 | ||||
| 删除元素 | ||||
| 额外空间 | ||||
| 数据预处理 | / | 排序 |
建树 |
建哈希表 |
| 数据是否有序 | 无序 | 有序 | 有序 | 无序 |
线性搜索
- 通用性较好,无须任何数据预处理操作。假如我们仅需查询一次数据,那么其他三种方法的数据预处理的时间比线性搜索的时间还要更长。
- 适用于体量较小的数据,此情况下时间复杂度对效率影响较小。
- 适用于数据更新频率较高的场景,因为该方法不需要对数据进行任何额外维护。
二分查找
- 适用于大数据量的情况,效率表现稳定,最差时间复杂度为 O(logn) 。
- 数据量不能过大,因为存储数组需要连续的内存空间。
- 不适用于高频增删数据的场景,因为维护有序数组的开销较大。
哈希查找
- 适合对查询性能要求很高的场景,平均时间复杂度为 O(1) 。
- 不适合需要有序数据或范围查找的场景,因为哈希表无法维护数据的有序性。
- 对哈希函数和哈希冲突处理策略的依赖性较高,具有较大的性能劣化风险。
- 不适合数据量过大的情况,因为哈希表需要额外空间来最大程度地减少冲突,从而提供良好的查询性能。
树查找
- 适用于海量数据,因为树节点在内存中是分散存储的。
- 适合需要维护有序数据或范围查找的场景。
- 在持续增删节点的过程中,二叉搜索树可能产生倾斜,时间复杂度劣化至 O(n) 。
- 若使用 AVL 树或红黑树,则各项操作可在 O(logn) 效率下稳定运行,但维护树平衡的操作会增加额外的开销
排序
选择排序
selection sort的工作原理非常简单:开启一个循环,每轮从未排序区间选择最小的元素,将其放到已排序区间的末尾
设数组的长度为 n ,选择排序的算法流程如图所示
- 初始状态下,所有元素未排序,即未排序(索引)区间为 [0,n−1] 。
- 选取区间 [0,n−1] 中的最小元素,将其与索引 0 处的元素交换。完成后,数组前 1 个元素已排序。
- 选取区间 [1,n−1] 中的最小元素,将其与索引 1 处的元素交换。完成后,数组前 2 个元素已排序。
- 以此类推。经过 n−1 轮选择与交换后,数组前 n−1 个元素已排序。
- 仅剩的一个元素必定是最大元素,无须排序,因此数组排序完成
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
/* 选择排序 */
void SelectionSort(int[] nums) {
int n = nums.Length;
// 外循环:未排序区间为 [i, n-1]
for (int i = 0; i < n - 1; i++) {
// 内循环:找到未排序区间内的最小元素
int k = i;
for (int j = i + 1; j < n; j++) {
if (nums[j] < nums[k])
k = j; // 记录最小元素的索引
}
// 将该最小元素与未排序区间的首个元素交换
(nums[k], nums[i]) = (nums[i], nums[k]);
}
}
- 时间复杂度为 $O(n^2)$、非自适应排序:外循环共 n−1 轮,第一轮的未排序区间长度为 n ,最后一轮的未排序区间长度为 2 ,即各轮外循环分别包含 n、n−1、…、3、2 轮内循环,求和为 (n−1)(n+2)2 。
- 空间复杂度为 O(1)、原地排序:指针 i 和 j 使用常数大小的额外空间。
- 非稳定排序:元素
nums[i]有可能被交换至与其相等的元素的右边,导致两者的相对顺序发生改变
冒泡排序
Buble sort通过连续比较和交换相邻元素实现排序
设数组的长度为 n ,冒泡排序的步骤如图所示。
- 首先,对 n 个元素执行“冒泡”,将数组的最大元素交换至正确位置。
- 接下来,对剩余 n−1 个元素执行“冒泡”,将第二大元素交换至正确位置。
- 以此类推,经过 n−1 轮“冒泡”后,前 n−1 大的元素都被交换至正确位置。
- 仅剩的一个元素必定是最小元素,无须排序,因此数组排序完成
![]()
![]()
![]()
![]()
![]()
![]()
![]()
/* 冒泡排序 */
void BubbleSort(int[] nums) {
// 外循环:未排序区间为 [0, i]
for (int i = nums.Length - 1; i > 0; i--) {
// 内循环:将未排序区间 [0, i] 中的最大元素交换至该区间的最右端
for (int j = 0; j < i; j++) {
if (nums[j] > nums[j + 1]) {
// 交换 nums[j] 与 nums[j + 1]
(nums[j + 1], nums[j]) = (nums[j], nums[j + 1]);
}
}
}
}
/* 冒泡排序(标志优化)
如果某轮“冒泡”中没有执行任何交换操作,说明数组已经完成排序,可直接返回结果
因此,可以增加一个标志位来监测这种情况,一旦出现就立即返回*/
void BubbleSortWithFlag(int[] nums) {
// 外循环:未排序区间为 [0, i]
for (int i = nums.Length - 1; i > 0; i--) {
bool flag = false; // 初始化标志位
// 内循环:将未排序区间 [0, i] 中的最大元素交换至该区间的最右端
for (int j = 0; j < i; j++) {
if (nums[j] > nums[j + 1]) {
// 交换 nums[j] 与 nums[j + 1]
(nums[j + 1], nums[j]) = (nums[j], nums[j + 1]);
flag = true; // 记录交换元素
}
}
if (!flag) break; // 此轮“冒泡”未交换任何元素,直接跳出
}
}
- 时间复杂度为 O(n^2)、自适应排序:各轮“冒泡”遍历的数组长度依次为 n−1、n−2、…、2、1 ,总和为 (n−1)n/2 。在引入
flag优化后,最佳时间复杂度可达到 O(n) 。 - 空间复杂度为 O(1)、原地排序:指针 i 和 j 使用常数大小的额外空间。
- 稳定排序:由于在“冒泡”中遇到相等元素不交换
插入排序
insertion sort工作原理:在未排序区间选择一个基准元素,将该元素与其左侧已排序区间的元素逐一比较大小,并将该元素插入到正确的位置
插入排序的整体流程:
- 初始状态下,数组的第 1 个元素已完成排序。
- 选取数组的第 2 个元素作为
base,将其插入到正确位置后,数组的前 2 个元素已排序 - 选取第 3 个元素作为
base,将其插入到正确位置后,数组的前 3 个元素已排序。 - 以此类推,在最后一轮中,选取最后一个元素作为
base,将其插入到正确位置后,所有元素均已排序。
![]()
/* 插入排序 */
void InsertionSort(int[] nums) {
// 外循环:已排序区间为 [0, i-1]
for (int i = 1; i < nums.Length; i++) {
int bas = nums[i], j = i - 1;
// 内循环:将 base 插入到已排序区间 [0, i-1] 中的正确位置
while (j >= 0 && nums[j] > bas) {
nums[j + 1] = nums[j]; // 将 nums[j] 向右移动一位
j--;
}
nums[j + 1] = bas; // 将 base 赋值到正确位置
}
}
- 时间复杂度为 $O(n^2)$、自适应排序:在最差情况下,每次插入操作分别需要循环 n−1、n−2、…、2、1 次,求和得到 (n−1)n/2 ,因此时间复杂度为 $O(n^2)$ 。在遇到有序数据时,插入操作会提前终止。当输入数组完全有序时,插入排序达到最佳时间复杂度 O(n) 。
- 空间复杂度为 O(1)、原地排序:指针 i 和 j 使用常数大小的额外空间。
- 稳定排序:在插入操作过程中,我们会将元素插入到相等元素的右侧,不会改变它们的顺序
虽然冒泡排序、选择排序和插入排序的时间复杂度都为 $O(n^2)$ ,但在实际情况中,插入排序的使用频率显著高于冒泡排序和选择排序,主要有以下原因:
- 冒泡排序基于元素交换实现,需要借助一个临时变量,共涉及 3 个单元操作;插入排序基于元素赋值实现,仅需 1 个单元操作。因此,冒泡排序的计算开销通常比插入排序更高。
- 选择排序在任何情况下的时间复杂度都为 $O(n^2)$ 。如果给定一组部分有序的数据,插入排序通常比选择排序效率更高。
- 选择排序不稳定,无法应用于多级排序
快速排序
quick sort是一种基于分治策略的排序算法:核心操作是"哨兵划分",其目标是:选择数组中某个元素作为"基准数",将所有小于基准数的元素移动到其左侧,大于基准数的元素移动到其右侧
- 选取数组最左端元素作为基准数,初始化两个指针
i和j分别指向数组的两端。 - 设置一个循环,在每轮中使用
i(j)分别寻找第一个比基准数大(小)的元素,然后交换这两个元素。 - 循环执行步骤
2.,直到i和j相遇时停止,最后将基准数交换至两个子数组的分界线
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
/* 元素交换 */
void Swap(int[] nums, int i, int j) {
(nums[j], nums[i]) = (nums[i], nums[j]);
}
/* 哨兵划分 */
int Partition(int[] nums, int left, int right) {
// 以 nums[left] 为基准数
int i = left, j = right;
while (i < j) {
while (i < j && nums[j] >= nums[left])
j--; // 从右向左找首个小于基准数的元素
while (i < j && nums[i] <= nums[left])
i++; // 从左向右找首个大于基准数的元素
Swap(nums, i, j); // 交换这两个元素
}
Swap(nums, i, left); // 将基准数交换至两子数组的分界线
return i; // 返回基准数的索引
}
/* 快速排序 */
void QuickSort(int[] nums, int left, int right) {
// 子数组长度为 1 时终止递归
if (left >= right)
return;
// 哨兵划分
int pivot = Partition(nums, left, right);
// 递归左子数组、右子数组
QuickSort(nums, left, pivot - 1);
QuickSort(nums, pivot + 1, right);
}
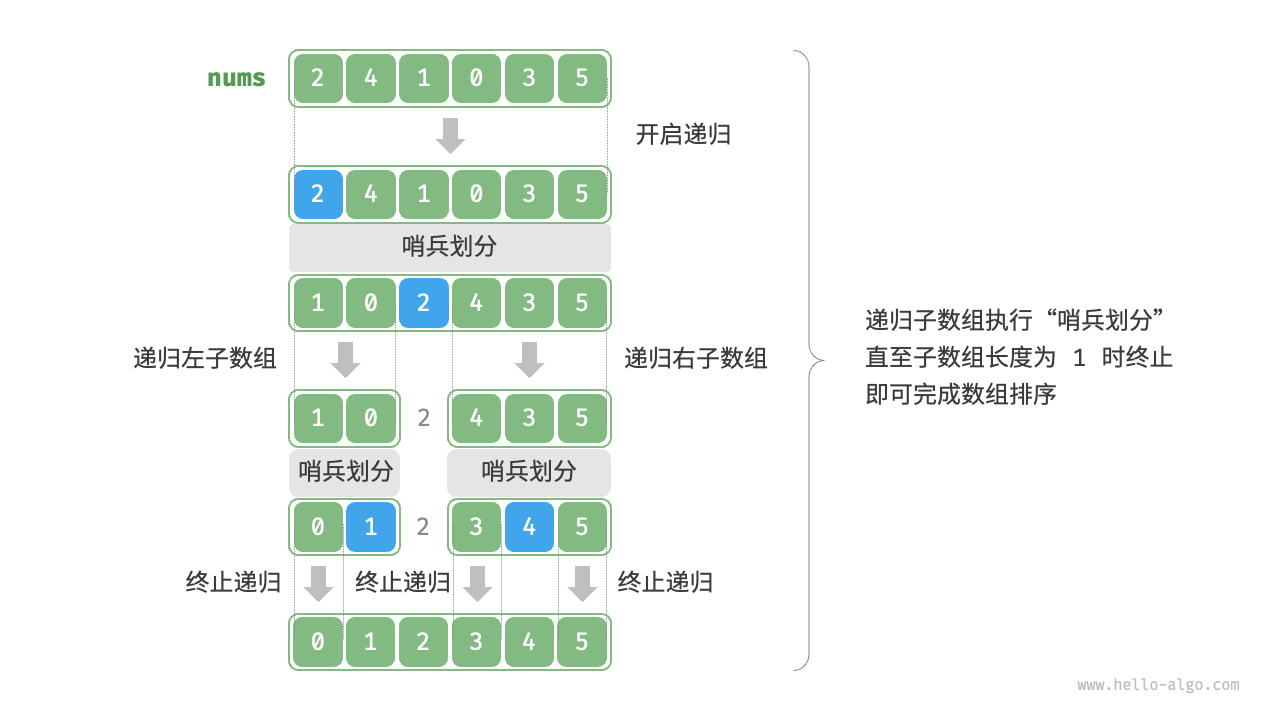
- 时间复杂度为 O(nlogn)、非自适应排序:在平均情况下,哨兵划分的递归层数为 logn ,每层中的总循环数为 n ,总体使用 O(nlogn) 时间。在最差情况下,每轮哨兵划分操作都将长度为 n 的数组划分为长度为 0 和 n−1 的两个子数组,此时递归层数达到 n ,每层中的循环数为 n ,总体使用 $O(n^2)$ 时间。
- 空间复杂度为 O(n)、原地排序:在输入数组完全倒序的情况下,达到最差递归深度 n ,使用 O(n) 栈帧空间。排序操作是在原数组上进行的,未借助额外数组。
- 非稳定排序:在哨兵划分的最后一步,基准数可能会被交换至相等元素的右侧
尽管快速排序的平均时间复杂度与“归并排序”和“堆排序”相同,但通常快速排序的效率更高,主要有以下原因:
- 出现最差情况的概率很低:虽然快速排序的最差时间复杂度为 $O(n^2)$,没有归并排序稳定,但在绝大多数情况下,快速排序能在 O(nlogn) 的时间复杂度下运行。
- 缓存使用效率高:在执行哨兵划分操作时,系统可将整个子数组加载到缓存,因此访问元素的效率较高。而像“堆排序”这类算法需要跳跃式访问元素,从而缺乏这一特性。
- 复杂度的常数系数小:在上述三种算法中,快速排序的比较、赋值、交换等操作的总数量最少。这与“插入排序”比“冒泡排序”更快的原因类似。
基准数优化
快速排序在某些输入下的时间效率可能降低。举一个极端例子,假设输入数组是完全倒序的,由于我们选择最左端元素作为基准数,那么在哨兵划分完成后,基准数被交换至数组最右端,导致左子数组长度为 n−1、右子数组长度为 0 。如此递归下去,每轮哨兵划分后都有一个子数组的长度为 0 ,分治策略失效,快速排序退化为“冒泡排序”的近似形式。
为了尽量避免这种情况发生,我们可以优化哨兵划分中的基准数的选取策略。例如,我们可以随机选取一个元素作为基准数。然而,如果运气不佳,每次都选到不理想的基准数,效率仍然不尽如人意。
需要注意的是,编程语言通常生成的是“伪随机数”。如果我们针对伪随机数序列构建一个特定的测试样例,那么快速排序的效率仍然可能劣化。
为了进一步改进,我们可以在数组中选取三个候选元素(通常为数组的首、尾、中点元素),并将这三个候选元素的中位数作为基准数。这样一来,基准数“既不太小也不太大”的概率将大幅提升。当然,我们还可以选取更多候选元素,以进一步提高算法的稳健性。采用这种方法后,时间复杂度劣化至 $O(n^2)$ 的概率大大降低
/* 选取三个候选元素的中位数 */
int MedianThree(int[] nums, int left, int mid, int right) {
int l = nums[left], m = nums[mid], r = nums[right];
if ((l <= m && m <= r) || (r <= m && m <= l))
return mid; // m 在 l 和 r 之间
if ((m <= l && l <= r) || (r <= l && l <= m))
return left; // l 在 m 和 r 之间
return right;
}
/* 哨兵划分(三数取中值) */
int Partition(int[] nums, int left, int right) {
// 选取三个候选元素的中位数
int med = MedianThree(nums, left, (left + right) / 2, right);
// 将中位数交换至数组最左端
Swap(nums, left, med);
// 以 nums[left] 为基准数
int i = left, j = right;
while (i < j) {
while (i < j && nums[j] >= nums[left])
j--; // 从右向左找首个小于基准数的元素
while (i < j && nums[i] <= nums[left])
i++; // 从左向右找首个大于基准数的元素
Swap(nums, i, j); // 交换这两个元素
}
Swap(nums, i, left); // 将基准数交换至两子数组的分界线
return i; // 返回基准数的索引
}
尾递归优化
在某些输入下,快速排序可能占用空间较多。以完全有序的输入数组为例,设递归中的子数组长度为 m ,每轮哨兵划分操作都将产生长度为 0 的左子数组和长度为 m−1 的右子数组,这意味着每一层递归调用减少的问题规模非常小(只减少一个元素),递归树的高度会达到 n−1 ,此时需要占用 O(n) 大小的栈帧空间。
为了防止栈帧空间的累积,我们可以在每轮哨兵排序完成后,比较两个子数组的长度,仅对较短的子数组进行递归。由于较短子数组的长度不会超过 n/2 ,因此这种方法能确保递归深度不超过 logn ,从而将最差空间复杂度优化至 O(logn)
/* 快速排序(尾递归优化) */
void QuickSort(int[] nums, int left, int right) {
// 子数组长度为 1 时终止
while (left < right) {
// 哨兵划分操作
int pivot = Partition(nums, left, right);
// 对两个子数组中较短的那个执行快速排序
if (pivot - left < right - pivot) {
QuickSort(nums, left, pivot - 1); // 递归排序左子数组
left = pivot + 1; // 剩余未排序区间为 [pivot + 1, right]
} else {
QuickSort(nums, pivot + 1, right); // 递归排序右子数组
right = pivot - 1; // 剩余未排序区间为 [left, pivot - 1]
}
}
}
归并排序
merge sort是一种基于分治策略的排序算法
- 划分阶段:通过递归不断地将数组从中点处分开,将长数组的排序问题转换为短数组的排序问题。
- 合并阶段:当子数组长度为 1 时终止划分,开始合并,持续地将左右两个较短的有序数组合并为一个较长的有序数组,直至结束
“划分阶段”从顶至底递归地将数组从中点切分为两个子数组。
- 计算数组中点
mid,递归划分左子数组(区间[left, mid])和右子数组(区间[mid + 1, right])。 - 递归执行步骤
1.,直至子数组区间长度为 1 时终止。
“合并阶段”从底至顶地将左子数组和右子数组合并为一个有序数组。需要注意的是,从长度为 1 的子数组开始合并,合并阶段中的每个子数组都是有序的
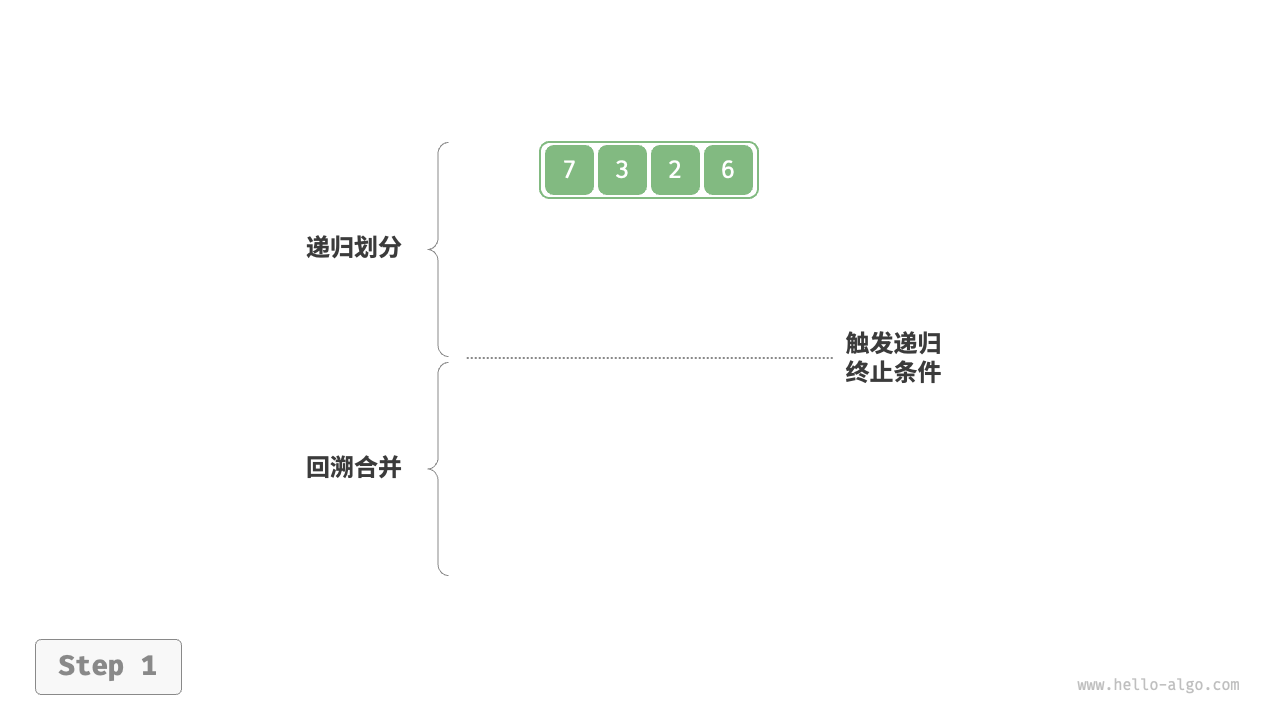
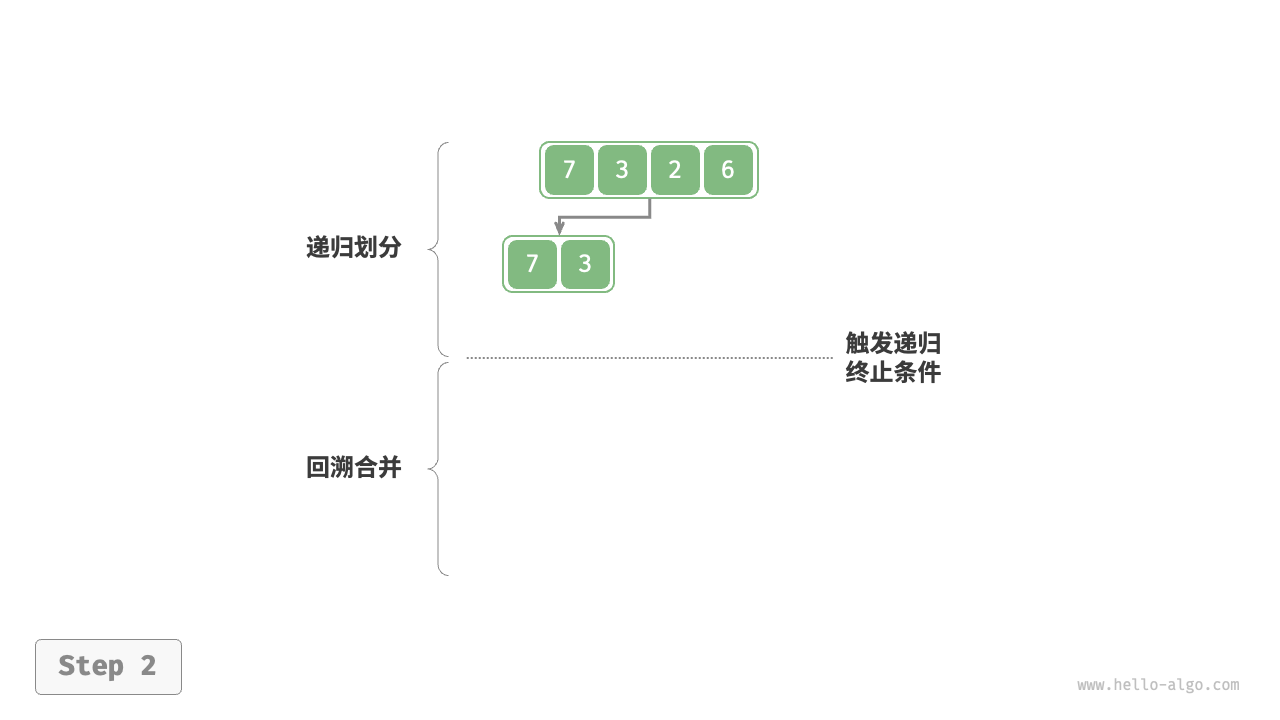
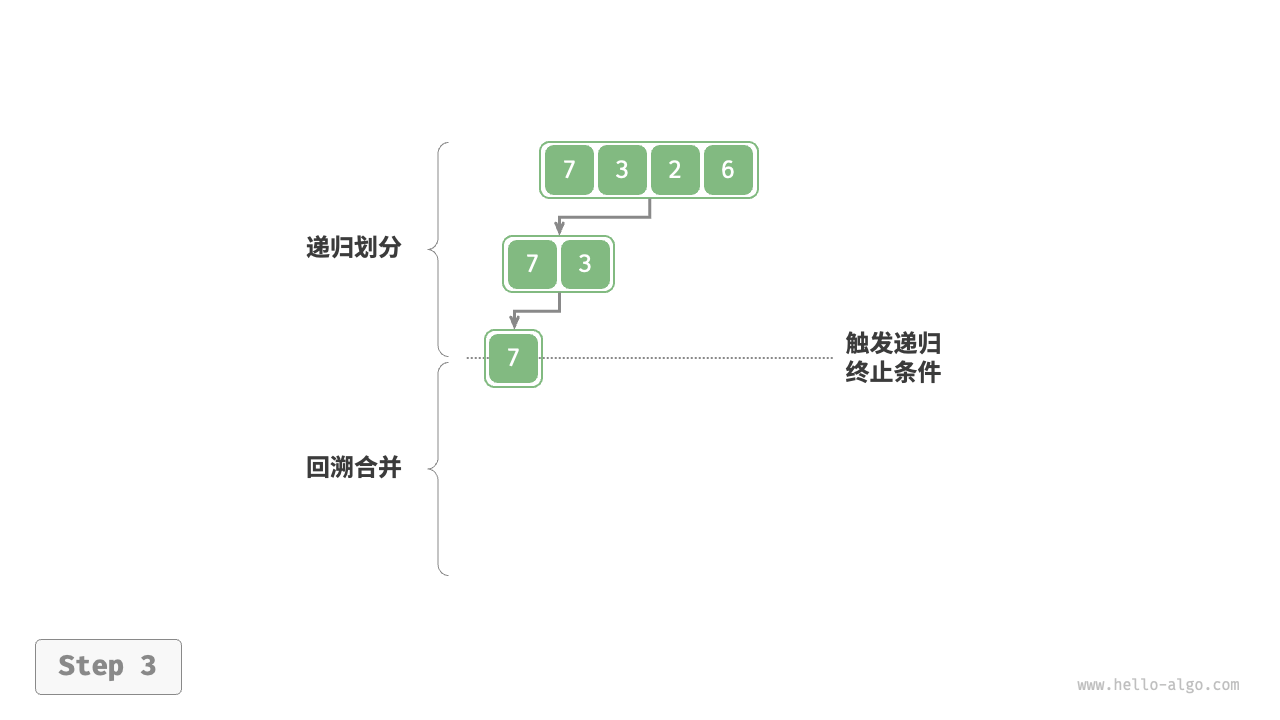
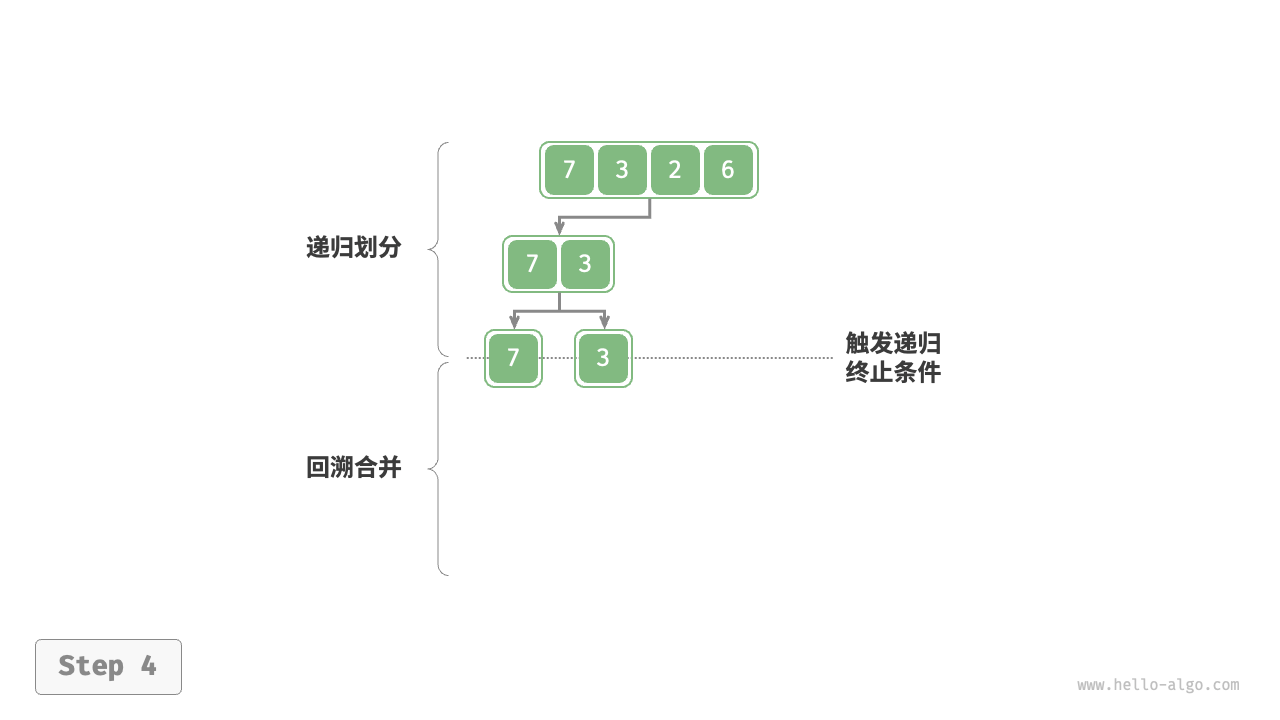
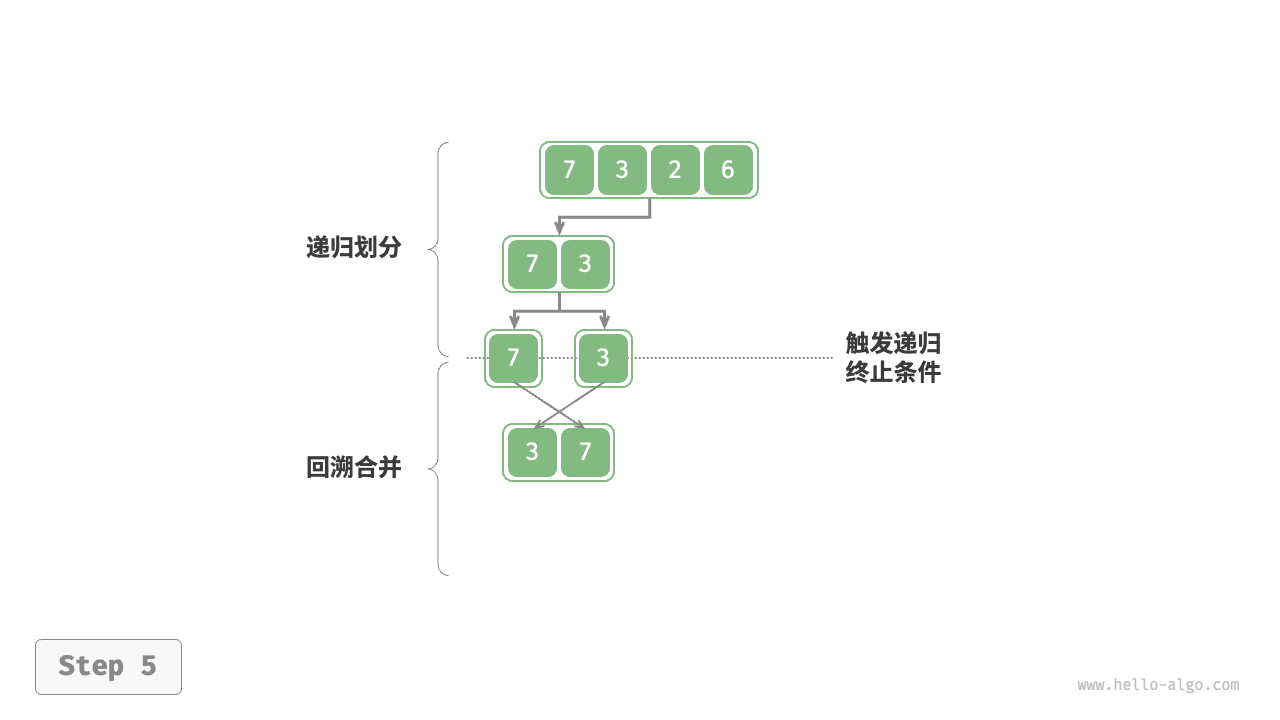
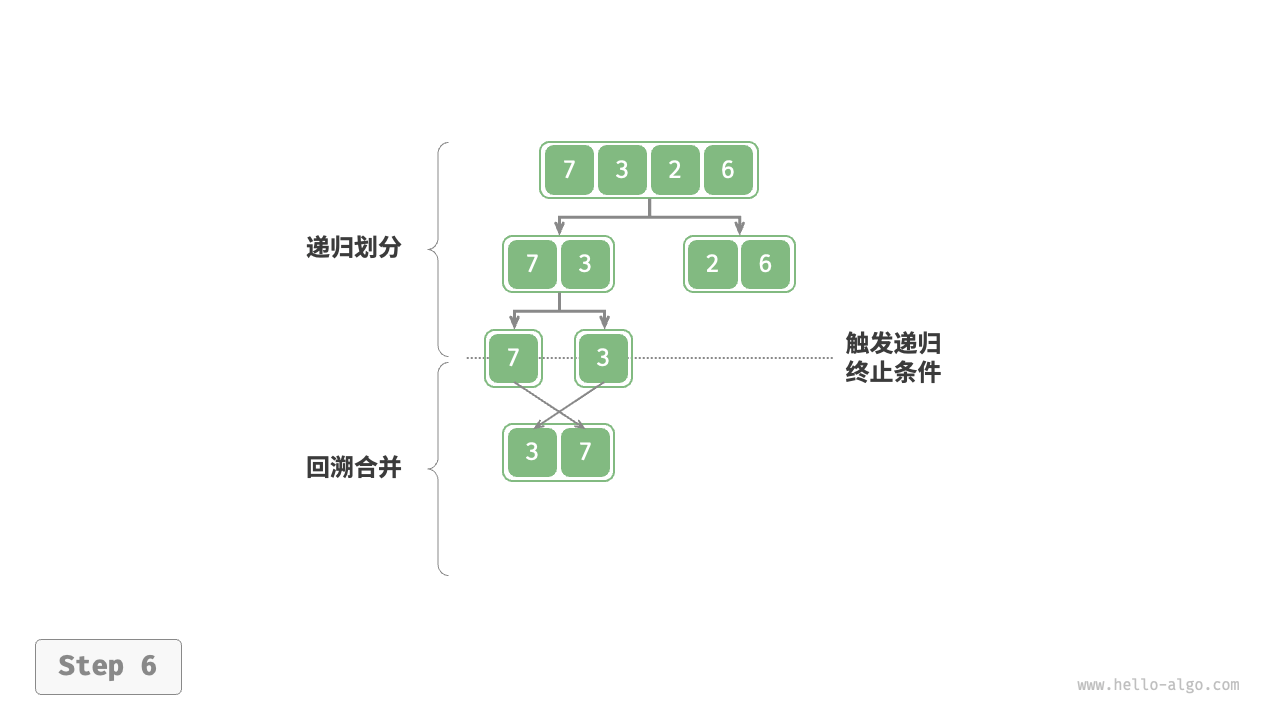
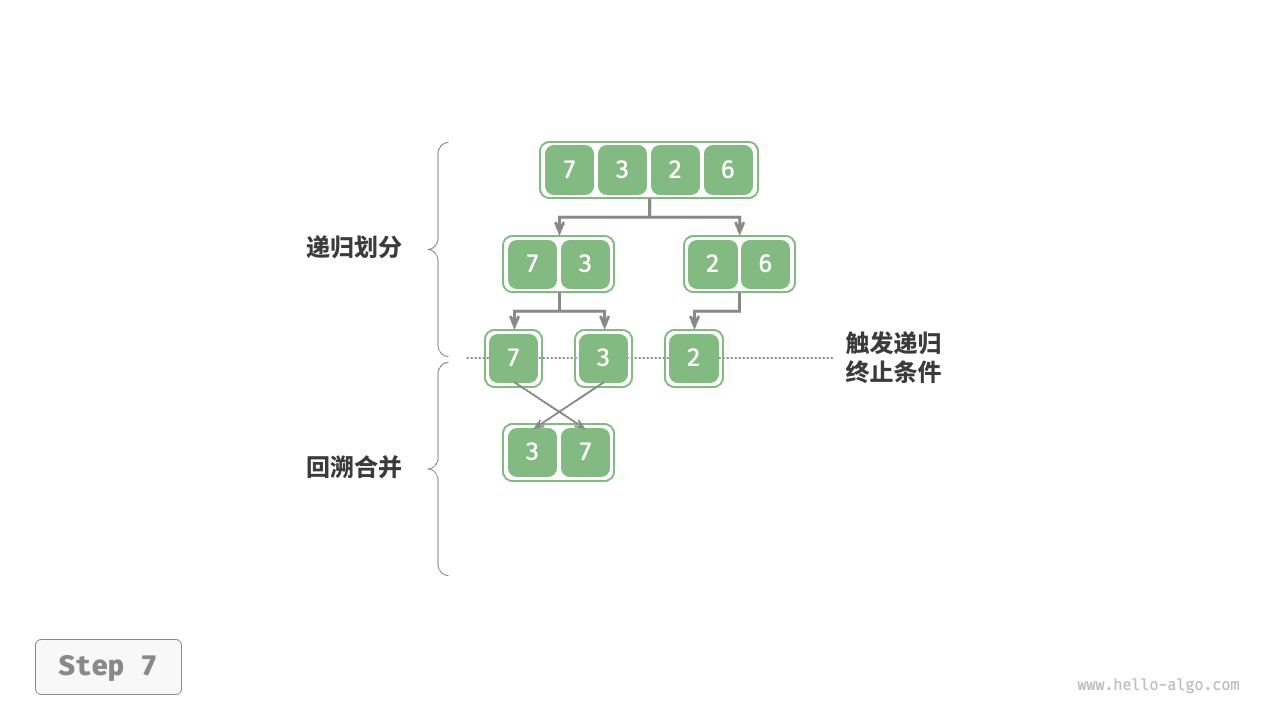
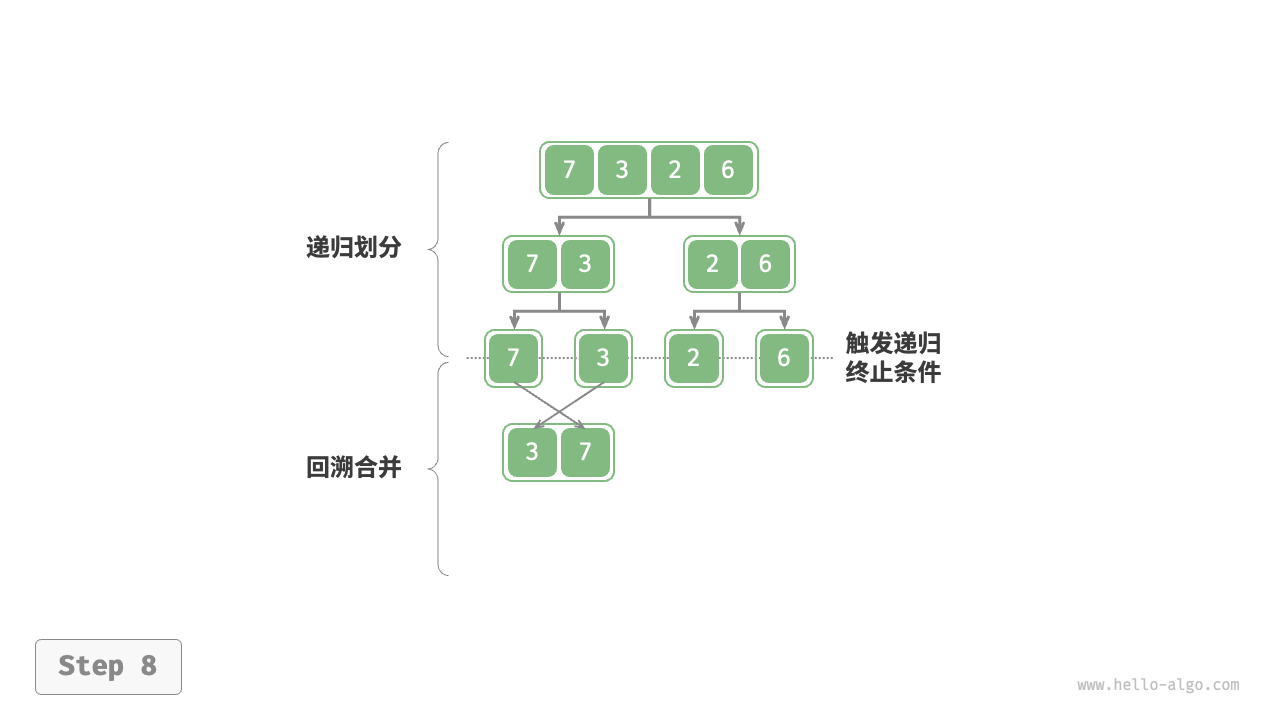
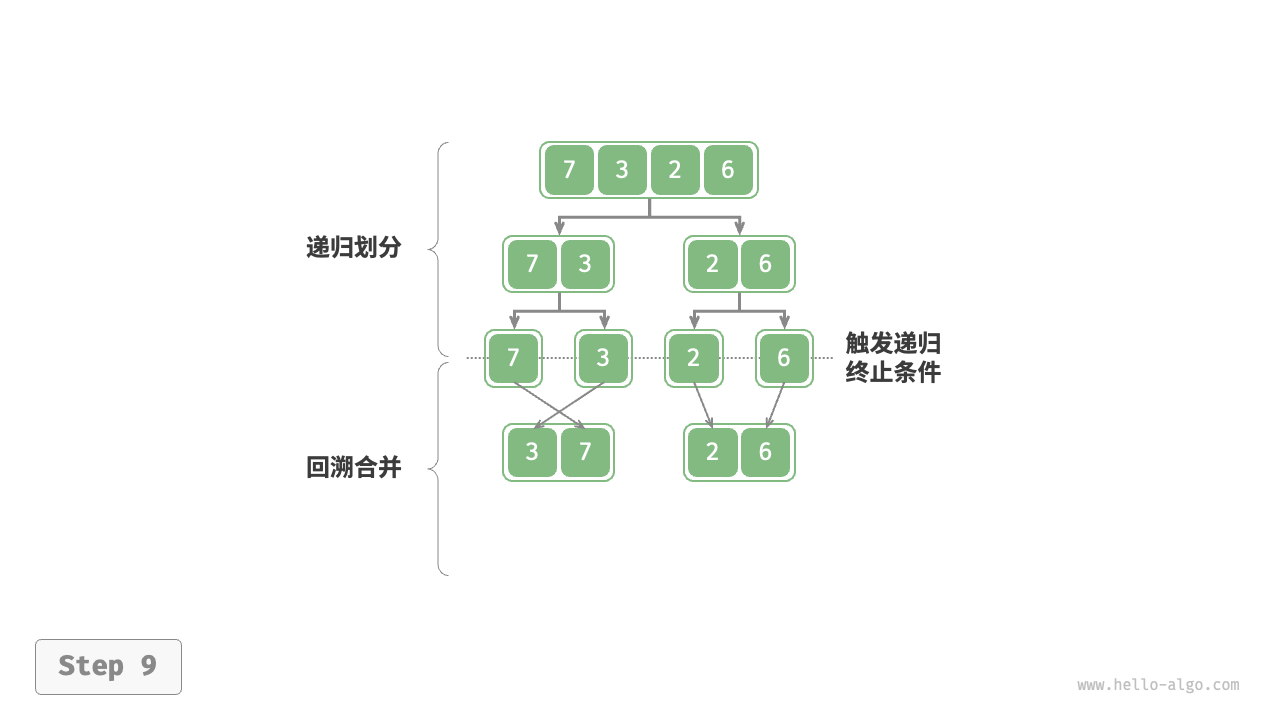
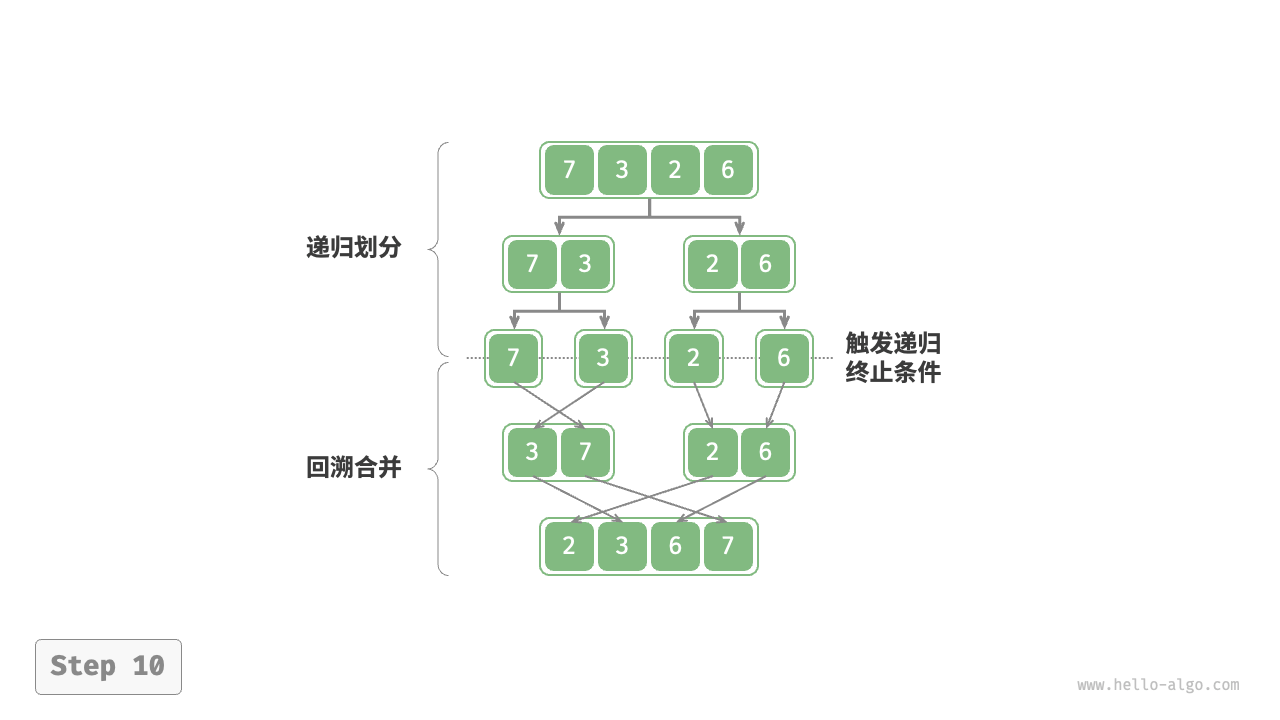
归并排序与二叉树后序遍历的递归顺序是一致的
- 后序遍历:先递归左子树,再递归右子树,最后处理根节点。
- 归并排序:先递归左子数组,再递归右子数组,最后处理合并。
归并排序的实现如以下代码所示。请注意,nums 的待合并区间为 [left, right] ,而 tmp 的对应区间为 [0, right - left]
/* 合并左子数组和右子数组 */
void Merge(int[] nums, int left, int mid, int right) {
// 左子数组区间为 [left, mid], 右子数组区间为 [mid+1, right]
// 创建一个临时数组 tmp ,用于存放合并后的结果
int[] tmp = new int[right - left + 1];
// 初始化左子数组和右子数组的起始索引
int i = left, j = mid + 1, k = 0;
// 当左右子数组都还有元素时,进行比较并将较小的元素复制到临时数组中
while (i <= mid && j <= right) {
if (nums[i] <= nums[j])
tmp[k++] = nums[i++];
else
tmp[k++] = nums[j++];
}
// 将左子数组和右子数组的剩余元素复制到临时数组中
while (i <= mid) {
tmp[k++] = nums[i++];
}
while (j <= right) {
tmp[k++] = nums[j++];
}
// 将临时数组 tmp 中的元素复制回原数组 nums 的对应区间
for (k = 0; k < tmp.Length; ++k) {
nums[left + k] = tmp[k];
}
}
/* 归并排序 */
void MergeSort(int[] nums, int left, int right) {
// 终止条件
if (left >= right) return; // 当子数组长度为 1 时终止递归
// 划分阶段
int mid = left + (right - left) / 2; // 计算中点
MergeSort(nums, left, mid); // 递归左子数组
MergeSort(nums, mid + 1, right); // 递归右子数组
// 合并阶段
Merge(nums, left, mid, right);
}
- 时间复杂度为 O(nlogn)、非自适应排序:划分产生高度为 logn 的递归树,每层合并的总操作数量为 n ,因此总体时间复杂度为 O(nlogn)
- 空间复杂度为 O(n)、非原地排序:递归深度为 logn ,使用 O(logn) 大小的栈帧空间。合并操作需要借助辅助数组实现,使用 O(n) 大小的额外空间
- 稳定排序:在合并过程中,相等元素的次序保持不变
对于链表,归并排序相较于其他排序算法具有显著优势,可以将链表排序任务的空间复杂度优化至 O(1) 。
- 划分阶段:可以使用“迭代”替代“递归”来实现链表划分工作,从而省去递归使用的栈帧空间。
- 合并阶段:在链表中,节点增删操作仅需改变引用(指针)即可实现,因此合并阶段(将两个短有序链表合并为一个长有序链表)无须创建额外链表
堆排序
heap sort是基于堆数据结构实现的高效排序算法
- 输入数组并建立大顶堆。完成后,最大元素位于堆顶。
- 将堆顶元素(第一个元素)与堆底元素(最后一个元素)交换。完成交换后,堆的长度减 1 ,已排序元素数量加 1 。
- 从堆顶元素开始,从顶到底执行堆化操作(sift down)。完成堆化后,堆的性质得到修复。
- 循环执行第
2.步和第3.步。循环 n−1 轮后,即可完成数组排序
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
使用了与“堆”章节相同的从顶至底堆化 sift_down() 函数。值得注意的是,由于堆的长度会随着提取最大元素而减小,因此我们需要给 sift_down() 函数添加一个长度参数 n ,用于指定堆的当前有效长度
/* 堆的长度为 n ,从节点 i 开始,从顶至底堆化 */
void SiftDown(int[] nums, int n, int i) {
while (true) {
// 判断节点 i, l, r 中值最大的节点,记为 ma
int l = 2 * i + 1;
int r = 2 * i + 2;
int ma = i;
if (l < n && nums[l] > nums[ma])
ma = l;
if (r < n && nums[r] > nums[ma])
ma = r;
// 若节点 i 最大或索引 l, r 越界,则无须继续堆化,跳出
if (ma == i)
break;
// 交换两节点
(nums[ma], nums[i]) = (nums[i], nums[ma]);
// 循环向下堆化
i = ma;
}
}
/* 堆排序 */
void HeapSort(int[] nums) {
// 建堆操作:堆化除叶节点以外的其他所有节点
for (int i = nums.Length / 2 - 1; i >= 0; i--) {
SiftDown(nums, nums.Length, i);
}
// 从堆中提取最大元素,循环 n-1 轮
for (int i = nums.Length - 1; i > 0; i--) {
// 交换根节点与最右叶节点(交换首元素与尾元素)
(nums[i], nums[0]) = (nums[0], nums[i]);
// 以根节点为起点,从顶至底进行堆化
SiftDown(nums, i, 0);
}
}
- 时间复杂度为 O(nlogn)、非自适应排序:建堆操作使用 O(n) 时间。从堆中提取最大元素的时间复杂度为 O(logn) ,共循环 n−1 轮。
- 空间复杂度为 O(1)、原地排序:几个指针变量使用 O(1) 空间。元素交换和堆化操作都是在原数组上进行的。
- 非稳定排序:在交换堆顶元素和堆底元素时,相等元素的相对位置可能发生变化
桶排序
bucket sort是分治策略的一个典型应用,通过设置一些具有大小顺序的桶,每个桶对应一个数据范围,将数据平均分配到各个桶中.然后在每个桶中分别执行排序,最终按照桶的顺序将所有数据合并
- 初始化 k 个桶,将 n 个元素分配到 k 个桶中
- 对每个桶分别执行排序(这里采用编程语言的内置排序函数)
- 按照桶从小到大的顺序合并结果
![]()
/* 桶排序 */
void BucketSort(float[] nums) {
// 初始化 k = n/2 个桶,预期向每个桶分配 2 个元素
int k = nums.Length / 2;
List<List<float>> buckets = [];
for (int i = 0; i < k; i++) {
buckets.Add([]);
}
// 1. 将数组元素分配到各个桶中
foreach (float num in nums) {
// 输入数据范围为 [0, 1),使用 num * k 映射到索引范围 [0, k-1]
int i = (int)(num * k);
// 将 num 添加进桶 i
buckets[i].Add(num);
}
// 2. 对各个桶执行排序
foreach (List<float> bucket in buckets) {
// 使用内置排序函数,也可以替换成其他排序算法
bucket.Sort();
}
// 3. 遍历桶合并结果
int j = 0;
foreach (List<float> bucket in buckets) {
foreach (float num in bucket) {
nums[j++] = num;
}
}
}
桶排序适用于处理体量很大的数据。例如,输入数据包含 100 万个元素,由于空间限制,系统内存无法一次性加载所有数据。此时,可以将数据分成 1000 个桶,然后分别对每个桶进行排序,最后将结果合并。
- 时间复杂度为 O(n+k) :假设元素在各个桶内平均分布,那么每个桶内的元素数量为 nk 。假设排序单个桶使用 $O(nklognk)$ 时间,则排序所有桶使用 $O(nklognk)$ 时间。当桶数量 k 比较大时,时间复杂度则趋向于 O(n) 。合并结果时需要遍历所有桶和元素,花费 $O(n+k)$ 时间。在最差情况下,所有数据被分配到一个桶中,且排序该桶使用 $O(n^2)$ 时间。
- 空间复杂度为 O(n+k)、非原地排序:需要借助 k 个桶和总共 n 个元素的额外空间。
- 桶排序是否稳定取决于排序桶内元素的算法是否稳定
桶排序的时间复杂度理论上可以达到 O(n) ,关键在于将元素均匀分配到各个桶中,因为实际数据往往不是均匀分布的。例如,我们想要将淘宝上的所有商品按价格范围平均分配到 10 个桶中,但商品价格分布不均,低于 100 元的非常多,高于 1000 元的非常少。若将价格区间平均划分为 10 个,各个桶中的商品数量差距会非常大。
为实现平均分配,我们可以先设定一条大致的分界线,将数据粗略地分到 3 个桶中。分配完毕后,再将商品较多的桶继续划分为 3 个桶,直至所有桶中的元素数量大致相等
这种方法本质上是创建一棵递归树,目标是让叶节点的值尽可能平均。当然,不一定要每轮将数据划分为 3 个桶,具体划分方式可根据数据特点灵活选择
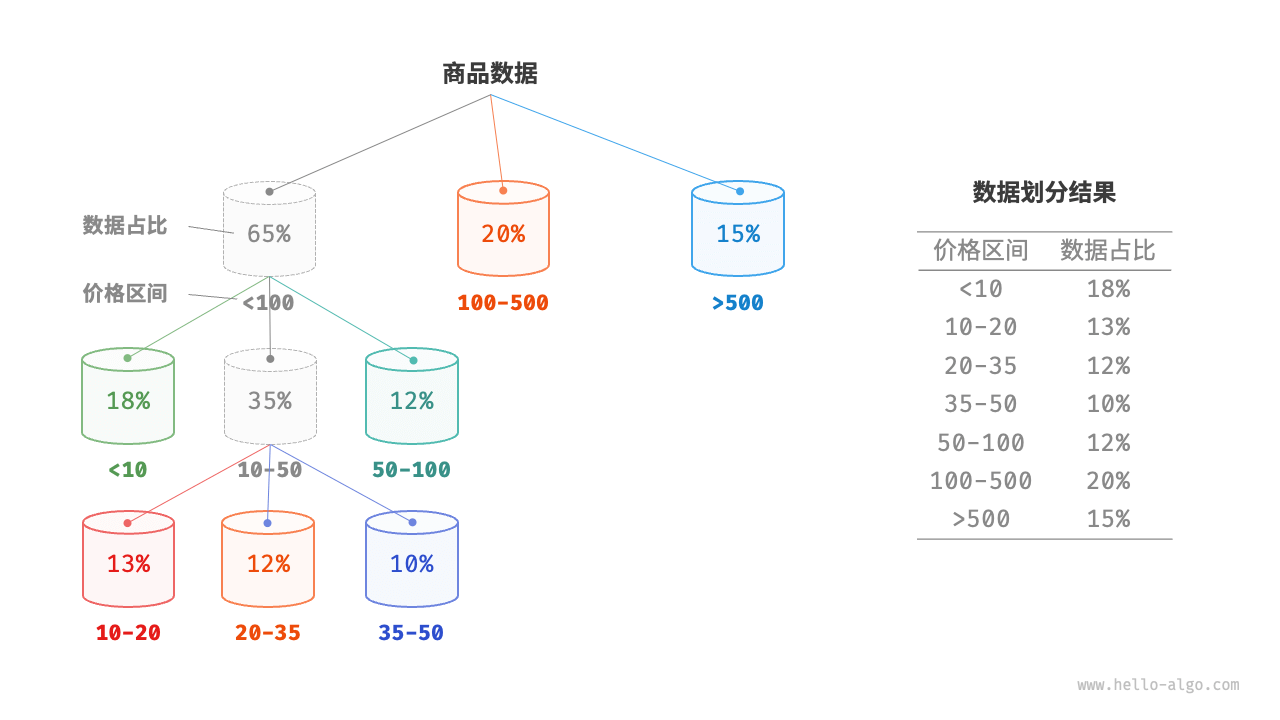
如果我们提前知道商品价格的概率分布,则可以根据数据概率分布设置每个桶的价格分界线。值得注意的是,数据分布并不一定需要特意统计,也可以根据数据特点采用某种概率模型进行近似
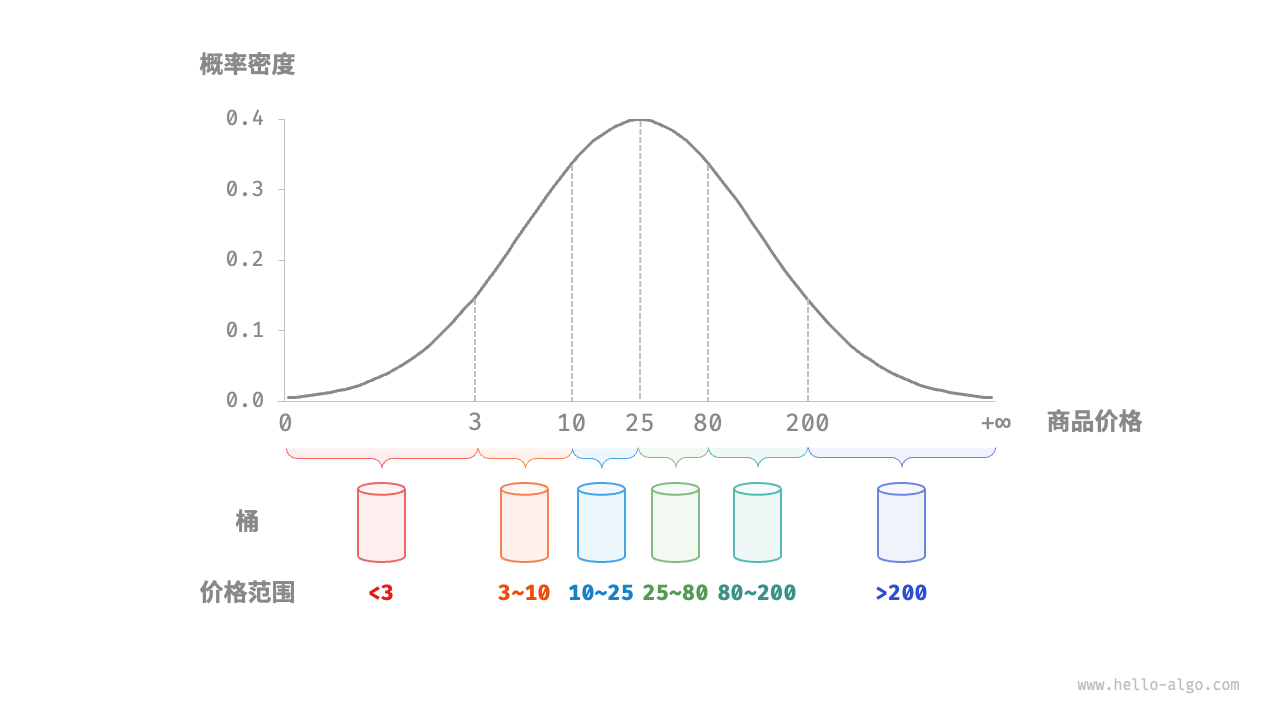
计数排序
counting sort通过统计元素数量来实现排序,通常应用于整数数组
定一个长度为 n 的数组 nums ,其中的元素都是“非负整数”,计数排序的整体流程如图所示
- 遍历数组,找出其中的最大数字,记为 m ,然后创建一个长度为 m+1 的辅助数组
counter - 借助
counter统计nums中各数字的出现次数,其中counter[num]对应数字num的出现次数。统计方法很简单,只需遍历nums(设当前数字为num),每轮将counter[num]增加 1 即可 - 由于
counter的各个索引天然有序,因此相当于所有数字已经排序好了。接下来,我们遍历counter,根据各数字出现次数从小到大的顺序填入nums即可
![]()
/* 计数排序 */
// 简单实现,无法用于排序对象
void CountingSortNaive(int[] nums) {
// 1. 统计数组最大元素 m
int m = 0;
foreach (int num in nums) {
m = Math.Max(m, num);
}
// 2. 统计各数字的出现次数
// counter[num] 代表 num 的出现次数
int[] counter = new int[m + 1];
foreach (int num in nums) {
counter[num]++;
}
// 3. 遍历 counter ,将各元素填入原数组 nums
int i = 0;
for (int num = 0; num < m + 1; num++) {
for (int j = 0; j < counter[num]; j++, i++) {
nums[i] = num;
}
}
}
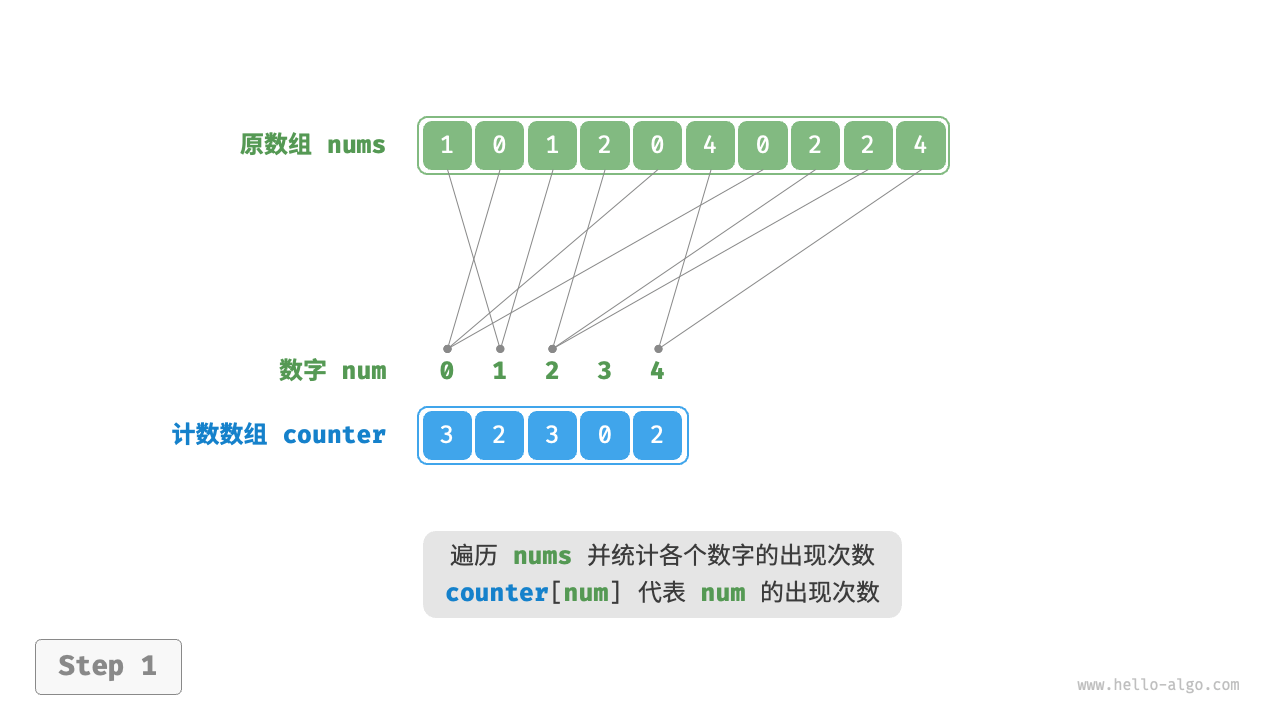
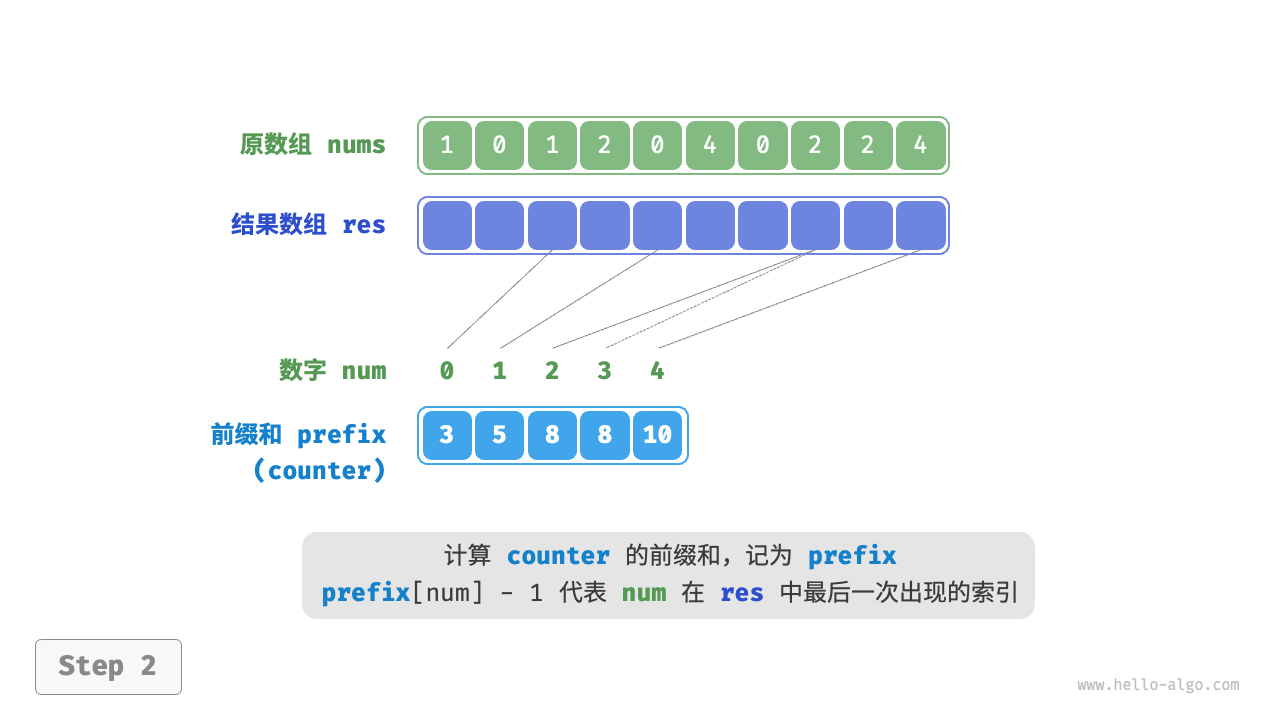
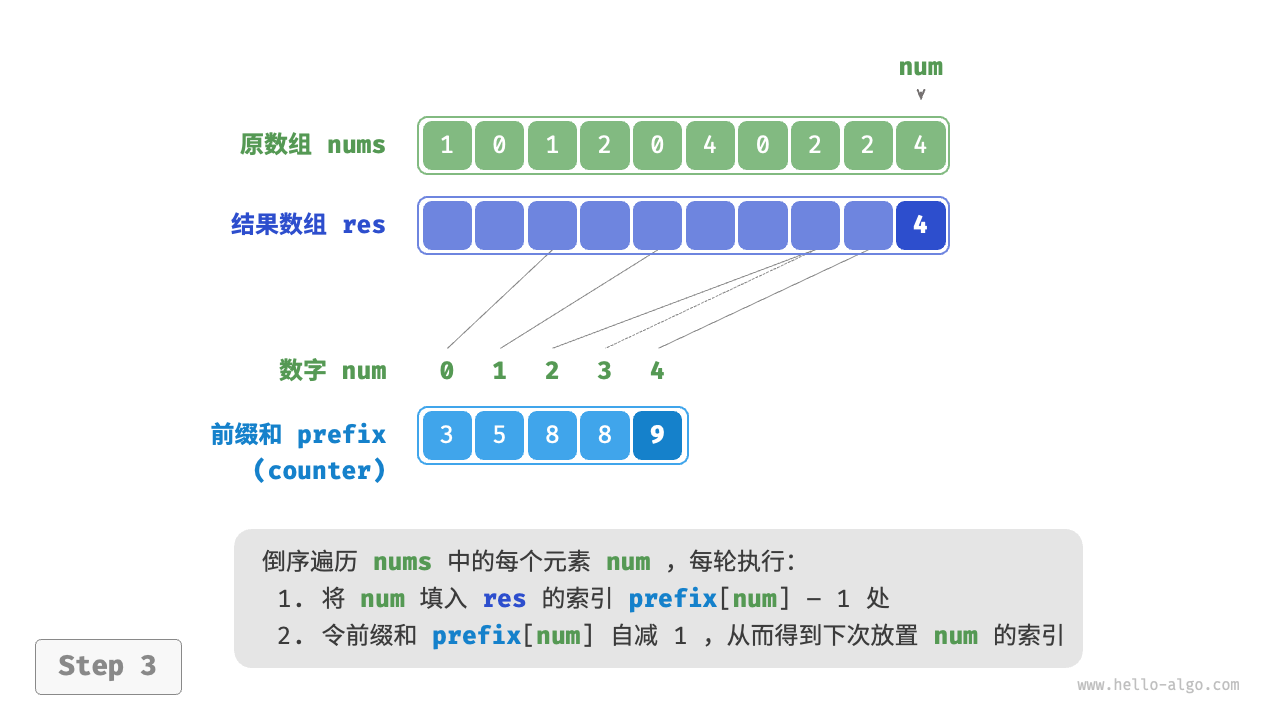
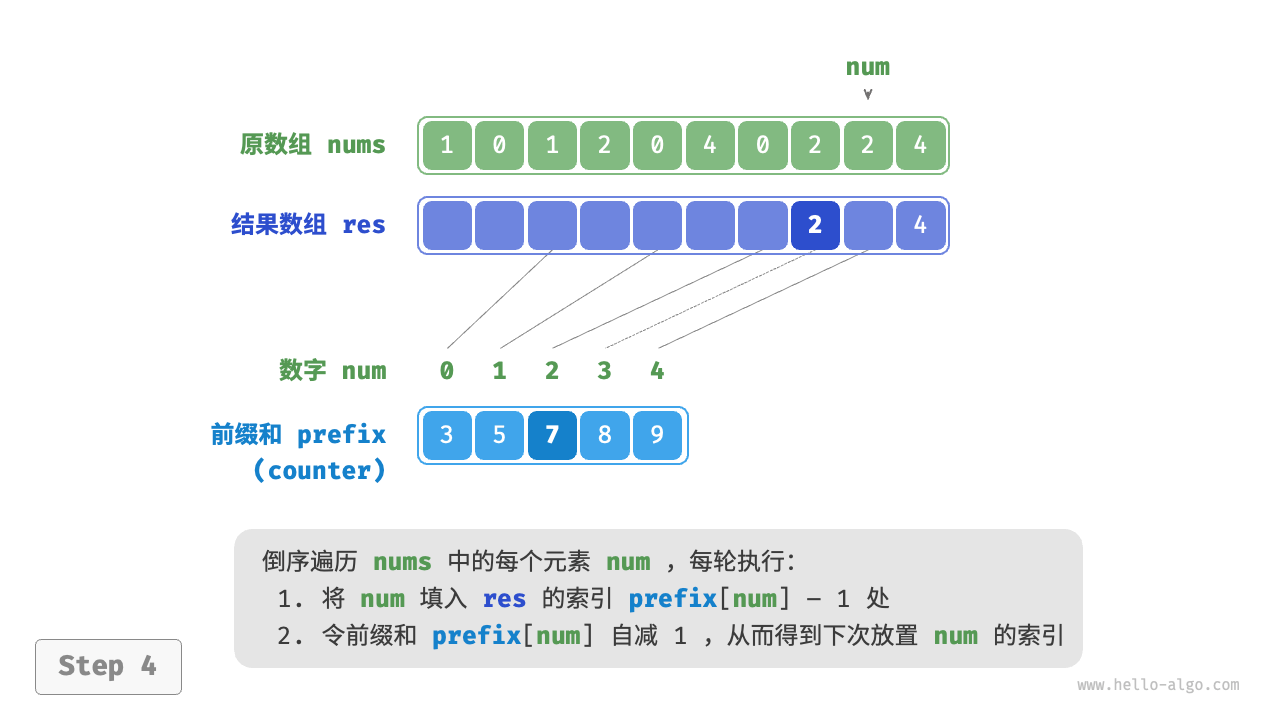
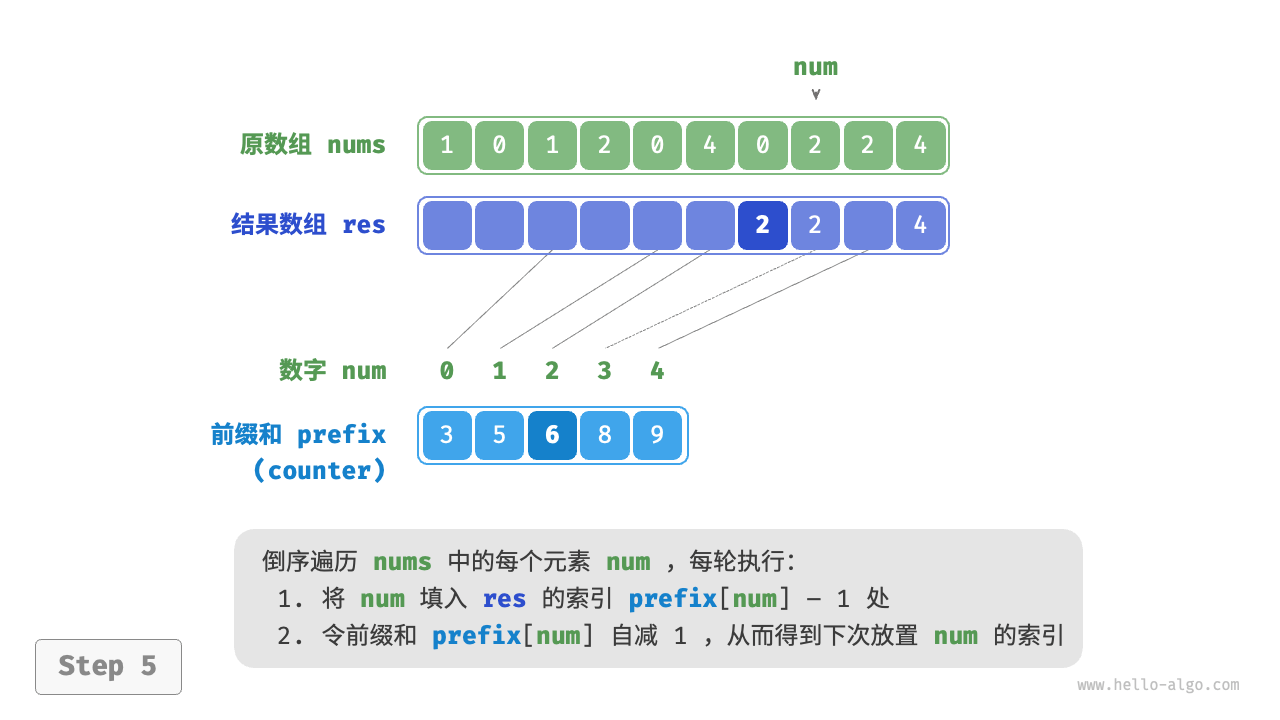
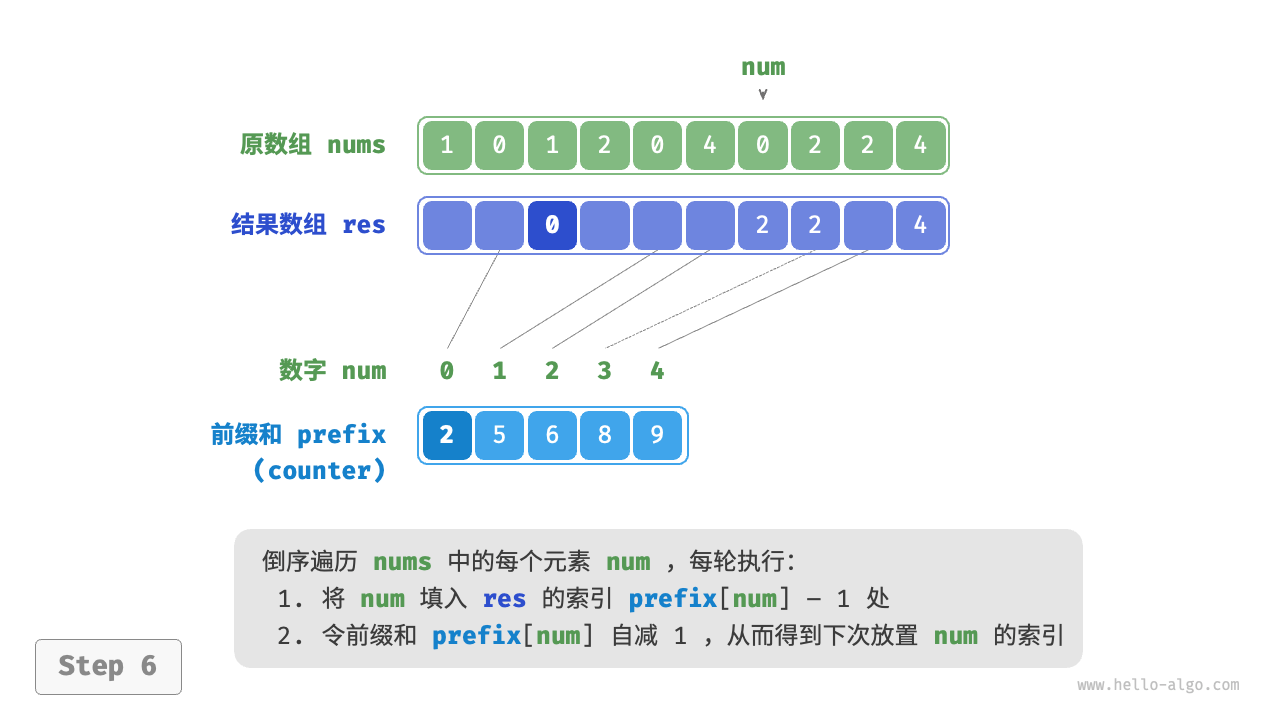
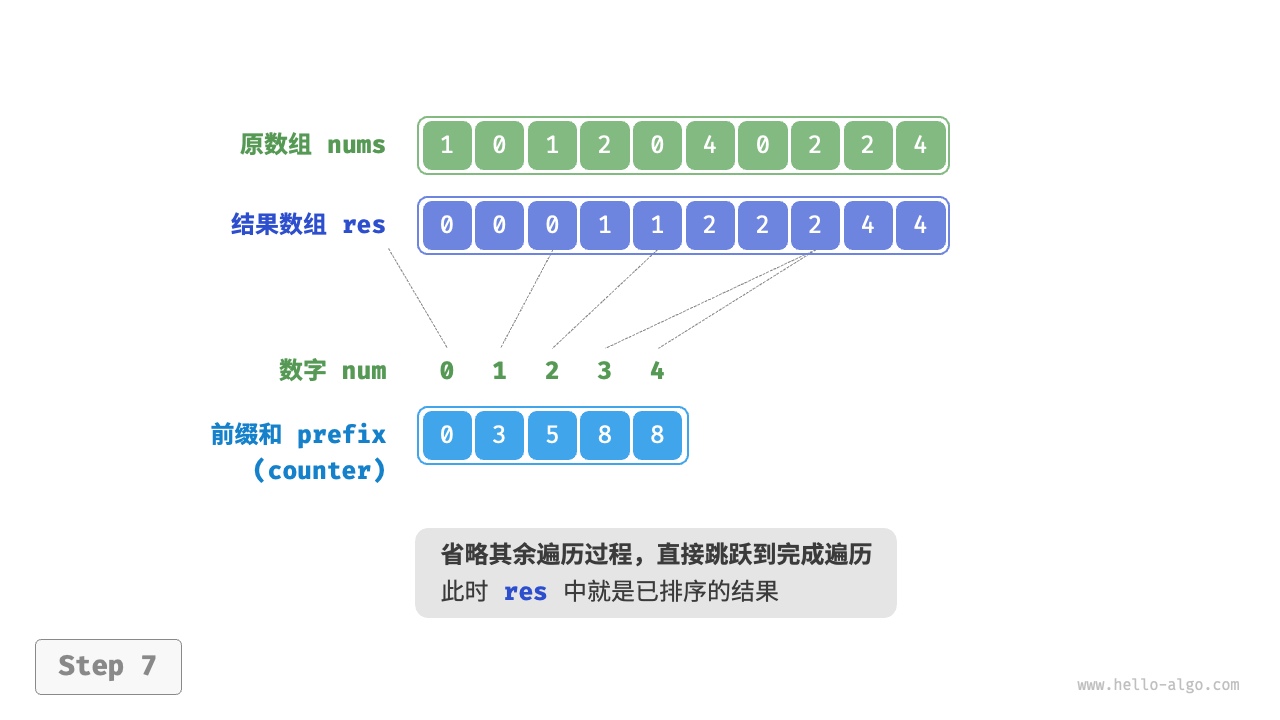
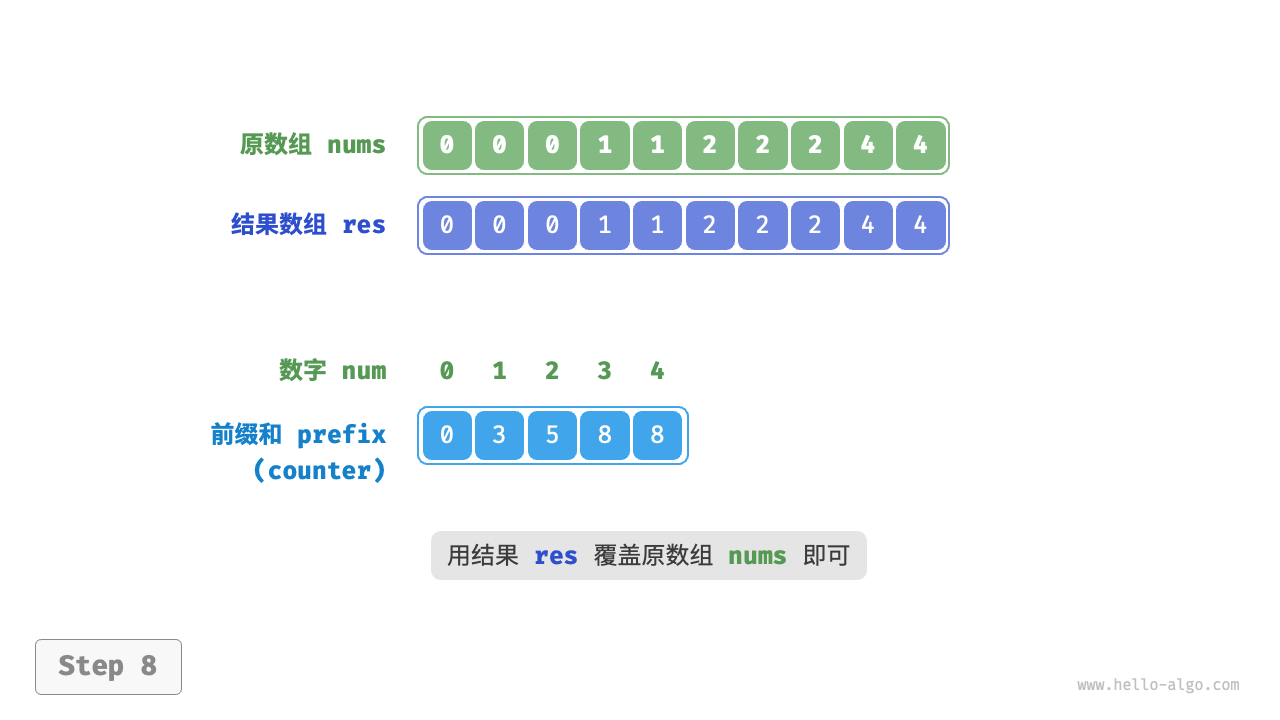
/* 计数排序 */
// 完整实现,可排序对象,并且是稳定排序
void CountingSort(int[] nums) {
// 1. 统计数组最大元素 m
int m = 0;
foreach (int num in nums) {
m = Math.Max(m, num);
}
// 2. 统计各数字的出现次数
// counter[num] 代表 num 的出现次数
int[] counter = new int[m + 1];
foreach (int num in nums) {
counter[num]++;
}
// 3. 求 counter 的前缀和,将“出现次数”转换为“尾索引”
// 即 counter[num]-1 是 num 在 res 中最后一次出现的索引
for (int i = 0; i < m; i++) {
counter[i + 1] += counter[i];
}
// 4. 倒序遍历 nums ,将各元素填入结果数组 res
// 初始化数组 res 用于记录结果
int n = nums.Length;
int[] res = new int[n];
for (int i = n - 1; i >= 0; i--) {
int num = nums[i];
res[counter[num] - 1] = num; // 将 num 放置到对应索引处
counter[num]--; // 令前缀和自减 1 ,得到下次放置 num 的索引
}
// 使用结果数组 res 覆盖原数组 nums
for (int i = 0; i < n; i++) {
nums[i] = res[i];
}
}
前缀和:索引
i处的前缀和prefix[i]等于数组前i个元素之和
- 时间复杂度为 O(n+m)、非自适应排序 :涉及遍历
nums和遍历counter,都使用线性时间。一般情况下 n≫m ,时间复杂度趋于 O(n) 。 - 空间复杂度为 O(n+m)、非原地排序:借助了长度分别为 n 和 m 的数组
res和counter。 - 稳定排序:由于向
res中填充元素的顺序是“从右向左”的,因此倒序遍历nums可以避免改变相等元素之间的相对位置,从而实现稳定排序。实际上,正序遍历nums也可以得到正确的排序结果,但结果是非稳定的
计数排序只适用于非负整数。若想将其用于其他类型的数据,需要确保这些数据可以转换为非负整数,并且在转换过程中不能改变各个元素之间的相对大小关系。例如,对于包含负数的整数数组,可以先给所有数字加上一个常数,将全部数字转化为正数,排序完成后再转换回去。
计数排序适用于数据量大但数据范围较小的情况。比如,在上述示例中 m 不能太大,否则会占用过多空间。而当 n≪m 时,计数排序使用 O(m) 时间,可能比 O(nlogn) 的排序算法还要慢
基数排序
假设我们需要对 $n=10^6$ 个学号进行排序,而学号是一个 8 位数字,这意味着数据范围 $m=10^8$ 非常大,使用计数排序需要分配大量内存空间,而基数排序可以避免这种情况
radix sort的核心思想与记数排序一致,也通过统计个数来实现排序.在此基础上,基数排序利用数字各位之间的递进关系,依次对每一位进行排序,从而得到最终排序结果
以学号数据为例,假设数字的最低位是第 1 位,最高位是第 8 位,基数排序的流程如图所示
- 初始化位数 k=1
- 对学号的第 k 位执行“计数排序”。完成后,数据会根据第 k 位从小到大排序
- 将 k 增加 1 ,然后返回步骤
2.继续迭代,直到所有位都排序完成后结束
![]()
/* 获取元素 num 的第 k 位,其中 exp = 10^(k-1) */
int Digit(int num, int exp) {
// 传入 exp 而非 k 可以避免在此重复执行昂贵的次方计算
return (num / exp) % 10;
}
/* 计数排序(根据 nums 第 k 位排序) */
void CountingSortDigit(int[] nums, int exp) {
// 十进制的位范围为 0~9 ,因此需要长度为 10 的桶数组
int[] counter = new int[10];
int n = nums.Length;
// 统计 0~9 各数字的出现次数
for (int i = 0; i < n; i++) {
int d = Digit(nums[i], exp); // 获取 nums[i] 第 k 位,记为 d
counter[d]++; // 统计数字 d 的出现次数
}
// 求前缀和,将“出现个数”转换为“数组索引”
for (int i = 1; i < 10; i++) {
counter[i] += counter[i - 1];
}
// 倒序遍历,根据桶内统计结果,将各元素填入 res
int[] res = new int[n];
for (int i = n - 1; i >= 0; i--) {
int d = Digit(nums[i], exp);
int j = counter[d] - 1; // 获取 d 在数组中的索引 j
res[j] = nums[i]; // 将当前元素填入索引 j
counter[d]--; // 将 d 的数量减 1
}
// 使用结果覆盖原数组 nums
for (int i = 0; i < n; i++) {
nums[i] = res[i];
}
}
/* 基数排序 */
void RadixSort(int[] nums) {
// 获取数组的最大元素,用于判断最大位数
int m = int.MinValue;
foreach (int num in nums) {
if (num > m) m = num;
}
// 按照从低位到高位的顺序遍历
for (int exp = 1; exp <= m; exp *= 10) {
// 对数组元素的第 k 位执行计数排序
// k = 1 -> exp = 1
// k = 2 -> exp = 10
// 即 exp = 10^(k-1)
CountingSortDigit(nums, exp);
}
}
title:为什么从最低位开始排序?
在连续的排序轮次中,后一轮排序会覆盖前一轮排序的结果。举例来说,如果第一轮排序结果 a<b ,而第二轮排序结果 a>b ,那么第二轮的结果将取代第一轮的结果。由于数字的高位优先级高于低位,因此应该先排序低位再排序高位。
相较于计数排序,基数排序适用于数值范围较大的情况,但前提是数据必须可以表示为固定位数的格式,且位数不能过大。例如,浮点数不适合使用基数排序,因为其位数 k 过大,可能导致时间复杂度 O(nk)≫$O(n^2)$
- 时间复杂度为 O(nk)、非自适应排序:设数据量为 n、数据为 d 进制、最大位数为 k ,则对某一位执行计数排序使用 O(n+d) 时间,排序所有 k 位使用 O((n+d)k) 时间。通常情况下,d 和 k 都相对较小,时间复杂度趋向 O(n)
- 空间复杂度为 O(n+d)、非原地排序:与计数排序相同,基数排序需要借助长度为 n 和 d 的数组
res和counter - 稳定排序:当计数排序稳定时,基数排序也稳定;当计数排序不稳定时,基数排序无法保证得到正确的排序结果
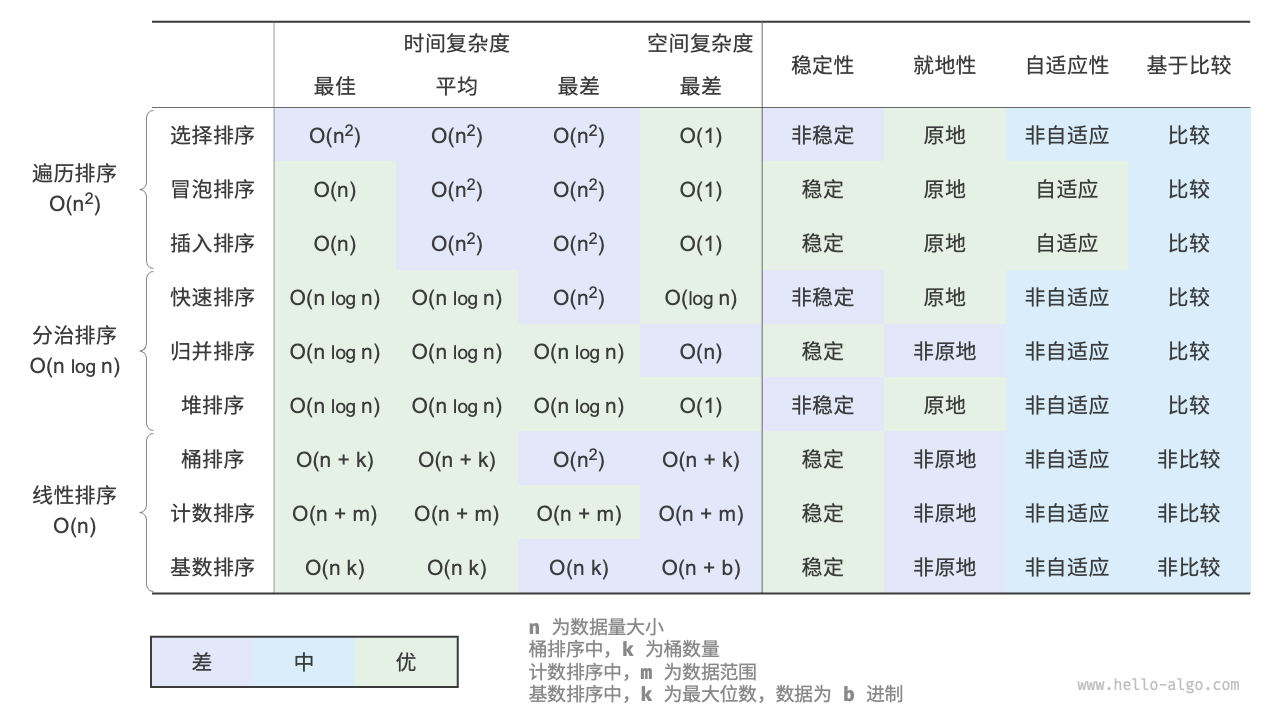
title:排序算法稳定性在什么情况下是必需的?
collapse:close
在现实中,我们有可能基于对象的某个属性进行排序。例如,学生有姓名和身高两个属性,我们希望实现一个多级排序:先按照姓名进行排序,得到 `(A, 180) (B, 185) (C, 170) (D, 170)` ;再对身高进行排序。由于排序算法不稳定,因此可能得到 `(D, 170) (C, 170) (A, 180) (B, 185)` 。
可以发现,学生 D 和 C 的位置发生了交换,姓名的有序性被破坏了
collapse:close
title:哨兵划分中“从右往左查找”与“从左往右查找”的顺序可以交换吗?
不行,当我们以最左端元素为基准数时,必须先“从右往左查找”再“从左往右查找”。这个结论有些反直觉,我们来剖析一下原因。
哨兵划分 `partition()` 的最后一步是交换 `nums[left]` 和 `nums[i]` 。完成交换后,基准数左边的元素都 `<=` 基准数,**这就要求最后一步交换前 `nums[left] >= nums[i]` 必须成立**。假设我们先“从左往右查找”,那么如果找不到比基准数更大的元素,**则会在 `i == j` 时跳出循环,此时可能 `nums[j] == nums[i] > nums[left]`**。也就是说,此时最后一步交换操作会把一个比基准数更大的元素交换至数组最左端,导致哨兵划分失败。
举个例子,给定数组 `[0, 0, 0, 0, 1]` ,如果先“从左向右查找”,哨兵划分后数组为 `[1, 0, 0, 0, 0]` ,这个结果是不正确的。
再深入思考一下,如果我们选择 `nums[right]` 为基准数,那么正好反过来,必须先“从左往右查找”
collapse:close
title:当数组中所有元素都相等时,快速排序的时间复杂度是 O(n2) 吗?该如何处理这种退化情况?
是的。对于这种情况,可以考虑通过哨兵划分将数组划分为三个部分:小于、等于、大于基准数。仅向下递归小于和大于的两部分。在该方法下,输入元素全部相等的数组,仅一轮哨兵划分即可完成排序。
分治
分治算法
divide and conquer 全称分而治之,是一种非常重要且常见的算法策略,分治通常基于递归实现
- 分(划分阶段):递归地将原问题分解为两个或多个子问题,直至到达最小子问题时终止。
- 治(合并阶段):从已知解的最小子问题开始,从底至顶地将子问题的解进行合并,从而构建出原问题的解
“归并排序”是分治策略的典型应用之一
- 分:递归地将原数组(原问题)划分为两个子数组(子问题),直到子数组只剩一个元素(最小子问题)。
- 治:从底至顶地将有序的子数组(子问题的解)进行合并,从而得到有序的原数组(原问题的解)
![]()
一个问题是否适合使用分治解决,通常可以参考以下几个判断依据:
- 问题可以分解:原问题可以分解成规模更小、类似的子问题,以及能够以相同方式递归地进行划分。
- 子问题是独立的:子问题之间没有重叠,互不依赖,可以独立解决。
- 子问题的解可以合并:原问题的解通过合并子问题的解得来。
分治不仅可以有效解决算法问题,还可以提升算法效率,排序算法中,快速排序、归并排序、堆排序相较于选择、冒泡、插入排序更快,就是因为它们应用了分治策略
分治可以提升效率的底层逻辑:
1. 操作数量优化
以“冒泡排序”为例,其处理一个长度为 n 的数组需要 $O(n^2)$ 时间。假设我们按照图所示的方式,将数组从中点处分为两个子数组,则划分需要 O(n) 时间,排序每个子数组需要 $O((n/2)^2)$ 时间,合并两个子数组需要 O(n) 时间,总体时间复杂度为:
$$
O\left(n+\left(\frac{n}{2}\right)^{2}\times 2+n\right)
=O\left(\frac{n^{2}}{2}+2 n\right)
$$
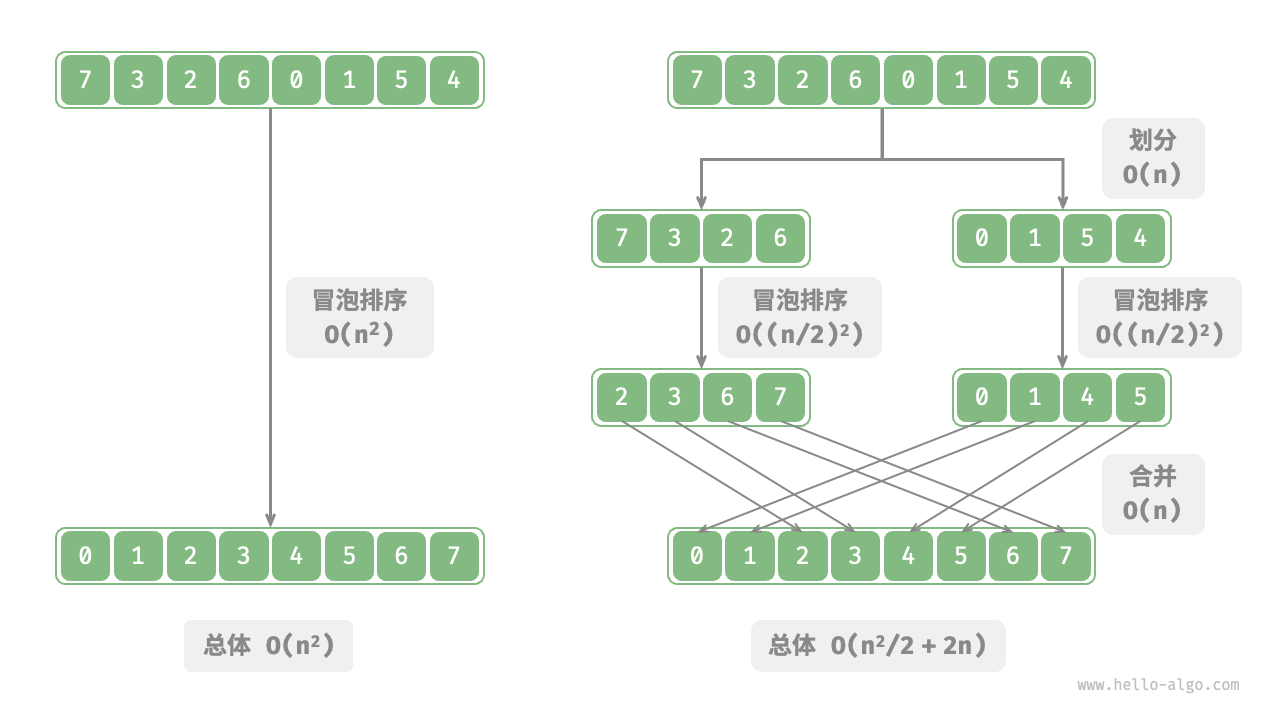
计算以下不等式,其左边和右边分别为划分前和划分后的操作总数:
$$
\begin{align}
n2>\frac{n2}{2}+2n\
n2-\frac{n2}{2}-2n>0\
n(n-4)>0
\end{align}
$$
这意味着当 n>4 时,划分后的操作数量更少,排序效率应该更高。请注意,划分后的时间复杂度仍然是平方阶 O(n2) ,只是复杂度中的常数项变小了。
进一步想,如果我们把子数组不断地再从中点处划分为两个子数组,直至子数组只剩一个元素时停止划分呢?这种思路实际上就是“归并排序”,时间复杂度为 O(nlogn) 。
再思考,如果我们多设置几个划分点,将原数组平均划分为 k 个子数组呢?这种情况与“桶排序”非常类似,它非常适合排序海量数据,理论上时间复杂度可以达到 O(n+k)
2. 并行计算优化
分治生成的子问题是相互独立的,因此通常可以并行解决。也就是说,分治不仅可以降低算法的时间复杂度,还有利于操作系统的并行优化。
并行优化在多核或多处理器的环境中尤其有效,因为系统可以同时处理多个子问题,更加充分地利用计算资源,从而显著减少总体的运行时间。
在图所示的“桶排序”中,我们将海量的数据平均分配到各个桶中,则可将所有桶的排序任务分散到各个计算单元,完成后再合并结果
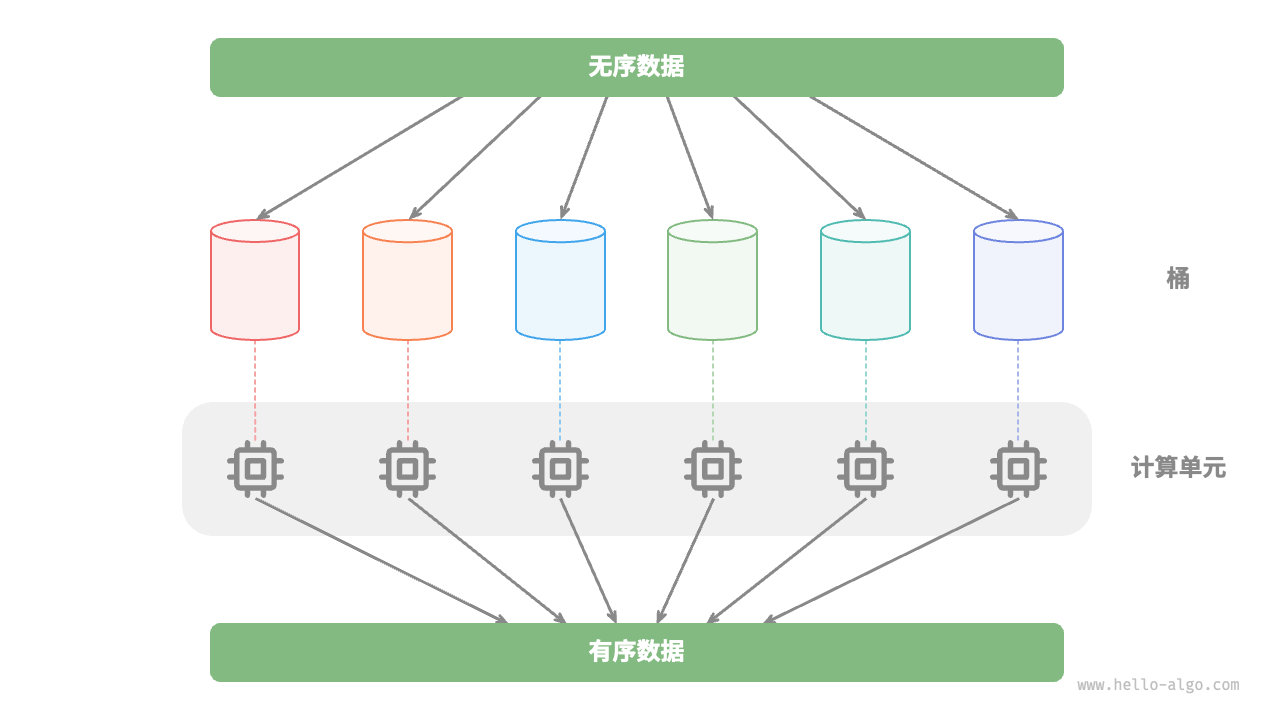
分治搜索策略
搜索算法分为两大类。
- 暴力搜索:它通过遍历数据结构实现,时间复杂度为 O(n) 。
- 自适应搜索:它利用特有的数据组织形式或先验信息,时间复杂度可达到 O(logn) 甚至 O(1)
实际上,时间复杂度为 O(logn) 的搜索算法通常是基于分治策略实现的,例如二分查找和树。
- 二分查找的每一步都将问题(在数组中搜索目标元素)分解为一个小问题(在数组的一半中搜索目标元素),这个过程一直持续到数组为空或找到目标元素为止。
- 树是分治思想的代表,在二叉搜索树、AVL 树、堆等数据结构中,各种操作的时间复杂度皆为 O(logn) 。
二分查找的分治策略如下所示:
- 问题可以分解:二分查找递归地将原问题(在数组中进行查找)分解为子问题(在数组的一半中进行查找),这是通过比较中间元素和目标元素来实现的。
- 子问题是独立的:在二分查找中,每轮只处理一个子问题,它不受其他子问题的影响。
- 子问题的解无须合并:二分查找旨在查找一个特定元素,因此不需要将子问题的解进行合并。当子问题得到解决时,原问题也会同时得到解决。
分治能够提升搜索效率,本质上是因为暴力搜索每轮只能排除一个选项,而分治搜索每轮可以排除一半选项。
在之前的章节中,二分查找是基于递推(迭代)实现的。现在我们基于分治(递归)来实现它
/* 二分查找:问题 f(i, j) */
int DFS(int[] nums, int target, int i, int j) {
// 若区间为空,代表无目标元素,则返回 -1
if (i > j) {
return -1;
}
// 计算中点索引 m
int m = (i + j) / 2;
if (nums[m] < target) {
// 递归子问题 f(m+1, j)
return DFS(nums, target, m + 1, j);
} else if (nums[m] > target) {
// 递归子问题 f(i, m-1)
return DFS(nums, target, i, m - 1);
} else {
// 找到目标元素,返回其索引
return m;
}
}
/* 二分查找 */
int BinarySearch(int[] nums, int target) {
int n = nums.Length;
// 求解问题 f(0, n-1)
return DFS(nums, target, 0, n - 1);
}
回溯
backtracking algorithm是一种通过穷举来解决问题的方法,核心思想是从一个初始状态出发,暴力搜索所有可能的解决方案,当遇到正确的解则将其记录,直到找到解或尝试了所有可能选择都无法找到解为止
回溯算法通常采用"深度优先搜索"来遍历解空间
给定一棵二叉树,搜索并记录所有值为 7 的节点,请返回节点列表
/* 前序遍历:例题一 */
void PreOrder(TreeNode? root) {
if (root == null) {
return;
}
if (root.val == 7) {
// 记录解
res.Add(root);
}
PreOrder(root.left);
PreOrder(root.right);
}
![]()
之所以称之为回溯算法,是因为该算法在搜索解空间时会采用"尝试"与"回退
的策略,当算法在搜索过程中遇到某个状态无法继续前进或无法得到满足条件的解时,它会撤销上一步的选择,退回到之前的状态,并尝试其他可能的选择
在二叉树中搜索所有值为 7 的节点,请返回根节点到这些节点的路径。
/* 前序遍历:例题二 */
void PreOrder(TreeNode? root) {
if (root == null) {
return;
}
// 尝试
path.Add(root);
if (root.val == 7) {
// 记录解
res.Add(new List<TreeNode>(path));
}
PreOrder(root.left);
PreOrder(root.right);
// 回退
path.RemoveAt(path.Count - 1);
}
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
复杂的回溯问题通常包含一个或多个约束条件,约束条件通常可用于“剪枝”
在二叉树中搜索所有值为 7 的节点,请返回根节点到这些节点的路径,并要求路径中不包含值为 3 的节点
为了满足以上约束条件,我们需要添加剪枝操作:在搜索过程中,若遇到值为 3 的节点,则提前返回,不再继续搜索
/* 前序遍历:例题三 */
void PreOrder(TreeNode? root) {
// 剪枝
if (root == null || root.val == 3) {
return;
}
// 尝试
path.Add(root);
if (root.val == 7) {
// 记录解
res.Add(new List<TreeNode>(path));
}
PreOrder(root.left);
PreOrder(root.right);
// 回退
path.RemoveAt(path.Count - 1);
}
在搜索过程中,“剪掉”了不满足约束条件的搜索分支,避免许多无意义的尝试,从而提高了搜索效率
![]()
/* 回溯算法框架 */
void Backtrack(State state, List<Choice> choices, List<State> res) {
// 判断是否为解
if (IsSolution(state)) {
// 记录解
RecordSolution(state, res);
// 不再继续搜索
return;
}
// 遍历所有选择
foreach (Choice choice in choices) {
// 剪枝:判断选择是否合法
if (IsValid(state, choice)) {
// 尝试:做出选择,更新状态
MakeChoice(state, choice);
Backtrack(state, choices, res);
// 回退:撤销选择,恢复到之前的状态
UndoChoice(state, choice);
}
}
}
基于框架代码来解决例题三。状态 state 为节点遍历路径,选择 choices 为当前节点的左子节点和右子节点,结果 res 是路径列表:
/* 判断当前状态是否为解 */
bool IsSolution(List<TreeNode> state) {
return state.Count != 0 && state[^1].val == 7;
}
/* 记录解 */
void RecordSolution(List<TreeNode> state, List<List<TreeNode>> res) {
res.Add(new List<TreeNode>(state));
}
/* 判断在当前状态下,该选择是否合法 */
bool IsValid(List<TreeNode> state, TreeNode choice) {
return choice != null && choice.val != 3;
}
/* 更新状态 */
void MakeChoice(List<TreeNode> state, TreeNode choice) {
state.Add(choice);
}
/* 恢复状态 */
void UndoChoice(List<TreeNode> state, TreeNode choice) {
state.RemoveAt(state.Count - 1);
}
/* 回溯算法:例题三 */
void Backtrack(List<TreeNode> state, List<TreeNode> choices, List<List<TreeNode>> res) {
// 检查是否为解
if (IsSolution(state)) {
// 记录解
RecordSolution(state, res);
}
// 遍历所有选择
foreach (TreeNode choice in choices) {
// 剪枝:检查选择是否合法
if (IsValid(state, choice)) {
// 尝试:做出选择,更新状态
MakeChoice(state, choice);
// 进行下一轮选择
Backtrack(state, [choice.left!, choice.right!], res);
// 回退:撤销选择,恢复到之前的状态
UndoChoice(state, choice);
}
}
}
在找到值为 7 的节点后应该继续搜索,因此需要将记录解之后的 return 语句删除
![]()
比基于前序遍历的代码实现,基于回溯算法框架的代码实现虽然显得啰唆,但通用性更好。实际上,许多回溯问题可以在该框架下解决。我们只需根据具体问题来定义 state 和 choices ,并实现框架中的各个方法即可
常见的回溯算法术语
| 名词 | 定义 | 例题三 |
|---|---|---|
| 解(solution) | 解是满足问题特定条件的答案,可能有一个或多个 | 根节点到节点 |
| 约束条件(constraint) | 约束条件是问题中限制解的可行性的条件,通常用于剪枝 | 路径中不包含节点 |
| 状态(state) | 状态表示问题在某一时刻的情况,包括已经做出的选择 | 当前已访问的节点路径,即 path 节点列表 |
| 尝试(attempt) | 尝试是根据可用选择来探索解空间的过程,包括做出选择,更新状态,检查是否为解 | 递归访问左(右)子节点,将节点添加进 path ,判断节点的值是否为 |
| 回退(backtracking) | 回退指遇到不满足约束条件的状态时,撤销前面做出的选择,回到上一个状态 | 当越过叶节点、结束节点访问、遇到值为 |
| 剪枝(pruning) | 剪枝是根据问题特性和约束条件避免无意义的搜索路径的方法,可提高搜索效率 | 当遇到值为 |
回溯算法可用于解决许多搜索问题、约束满足问题和组合优化问题。
搜索问题:这类问题的目标是找到满足特定条件的解决方案。
- 全排列问题:给定一个集合,求出其所有可能的排列组合。
- 子集和问题:给定一个集合和一个目标和,找到集合中所有和为目标和的子集。
- 汉诺塔问题:给定三根柱子和一系列大小不同的圆盘,要求将所有圆盘从一根柱子移动到另一根柱子,每次只能移动一个圆盘,且不能将大圆盘放在小圆盘上。
约束满足问题:这类问题的目标是找到满足所有约束条件的解。
- n 皇后:在 n×n 的棋盘上放置 n 个皇后,使得它们互不攻击。
- 数独:在 9×9 的网格中填入数字 1 ~ 9 ,使得每行、每列和每个 3×3 子网格中的数字不重复。
- 图着色问题:给定一个无向图,用最少的颜色给图的每个顶点着色,使得相邻顶点颜色不同。
组合优化问题:这类问题的目标是在一个组合空间中找到满足某些条件的最优解
- 0-1 背包问题:给定一组物品和一个背包,每个物品有一定的价值和重量,要求在背包容量限制内,选择物品使得总价值最大。
- 旅行商问题:在一个图中,从一个点出发,访问所有其他点恰好一次后返回起点,求最短路径。
- 最大团问题:给定一个无向图,找到最大的完全子图,即子图中的任意两个顶点之间都有边相连。
请注意,对于许多组合优化问题,回溯不是最优解决方案
- 0-1 背包问题通常使用动态规划解决,以达到更高的时间效率。
- 旅行商是一个著名的 NP-Hard 问题,常用解法有遗传算法和蚁群算法等。
- 最大团问题是图论中的一个经典问题,可用贪心算法等启发式算法来解决
动态规划
dynamic programing是一个重要的算式范式,它将一个问题分解为一系列更小子问题,并通过存储子问题的解来避免重复计算,从而大幅提升时间效率


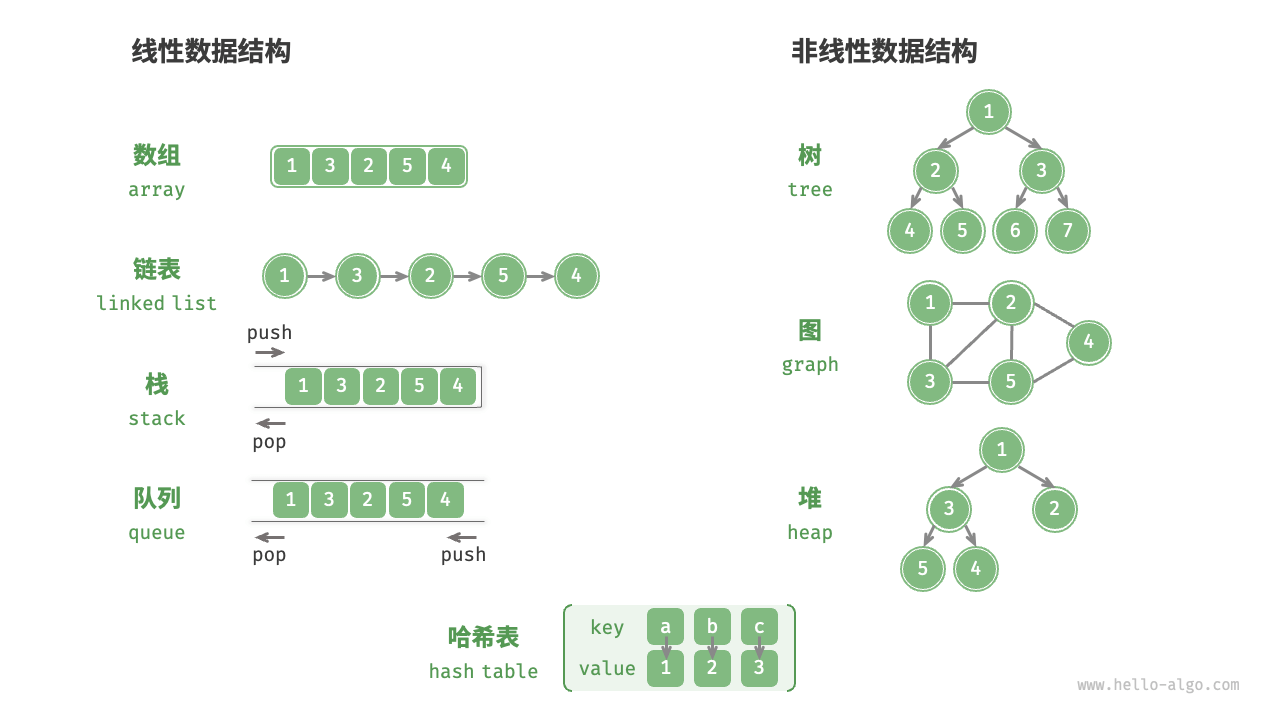
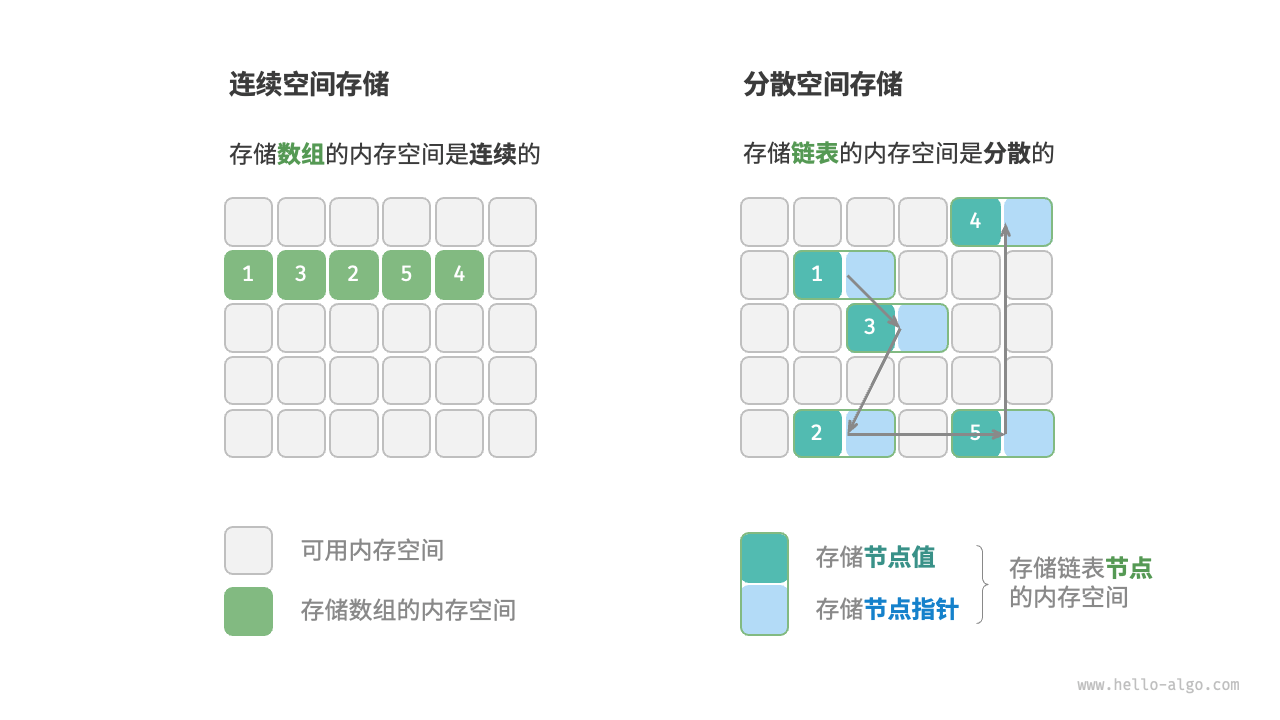
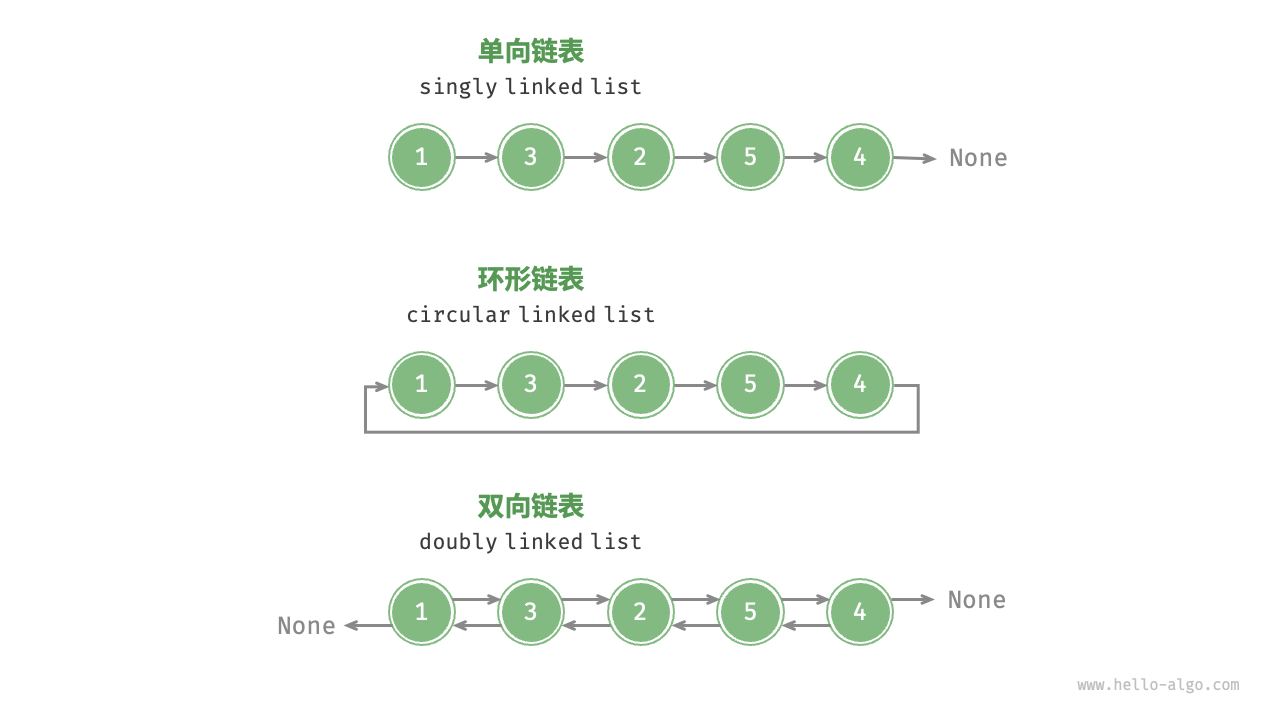
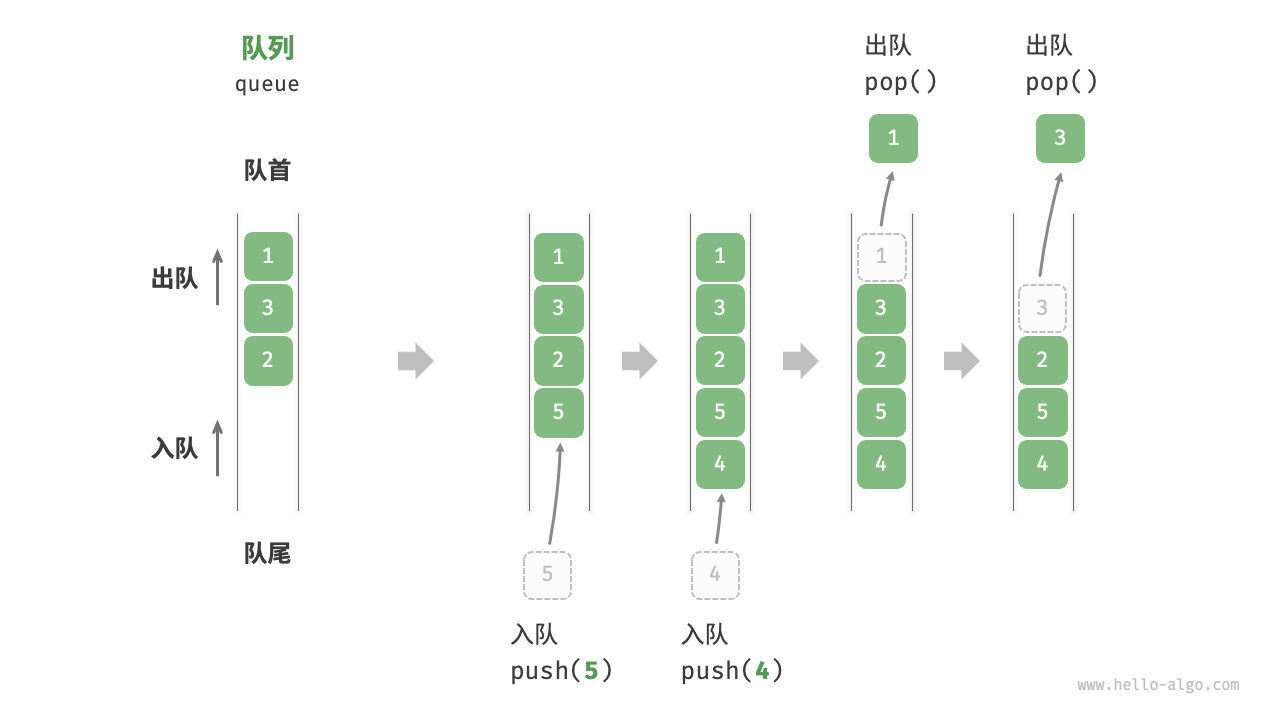
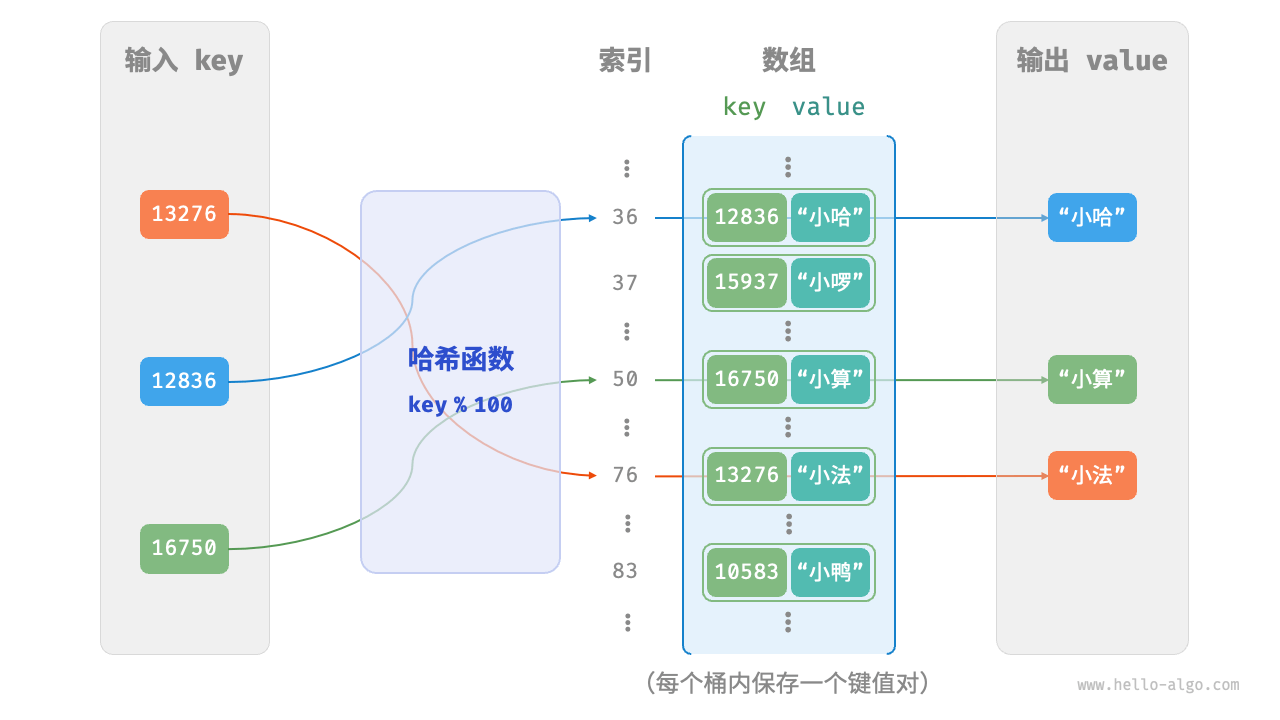

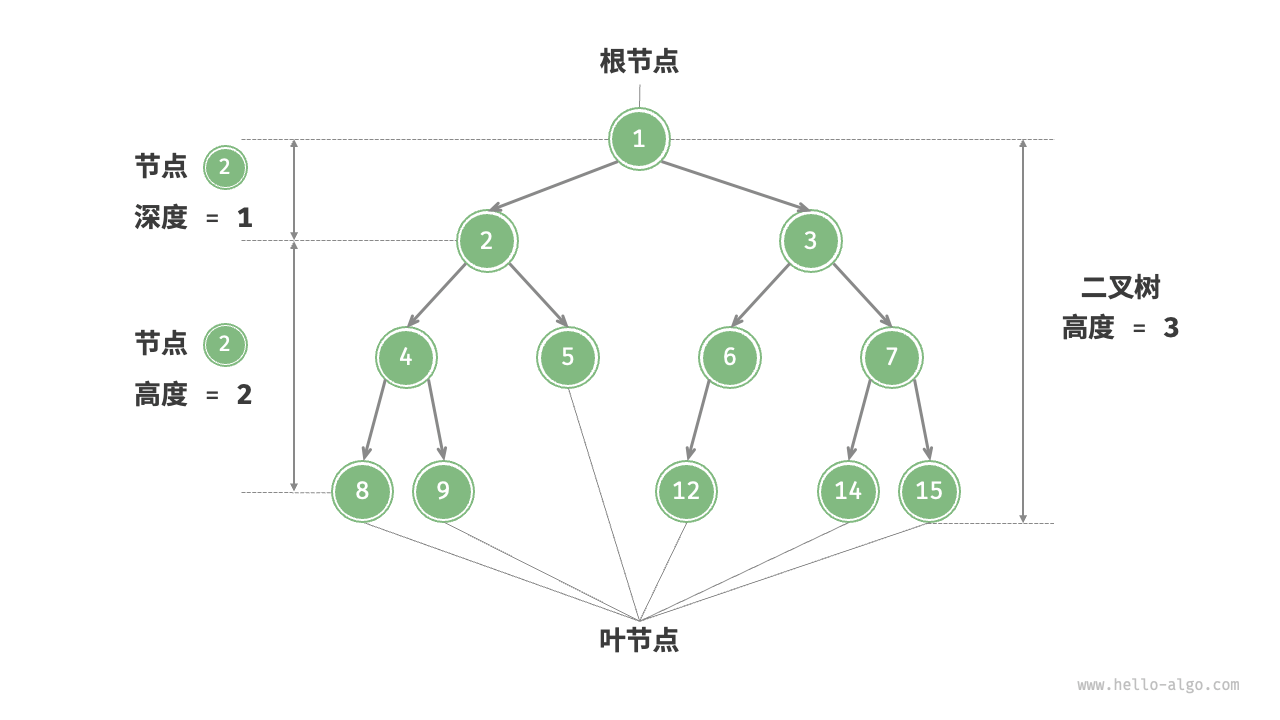
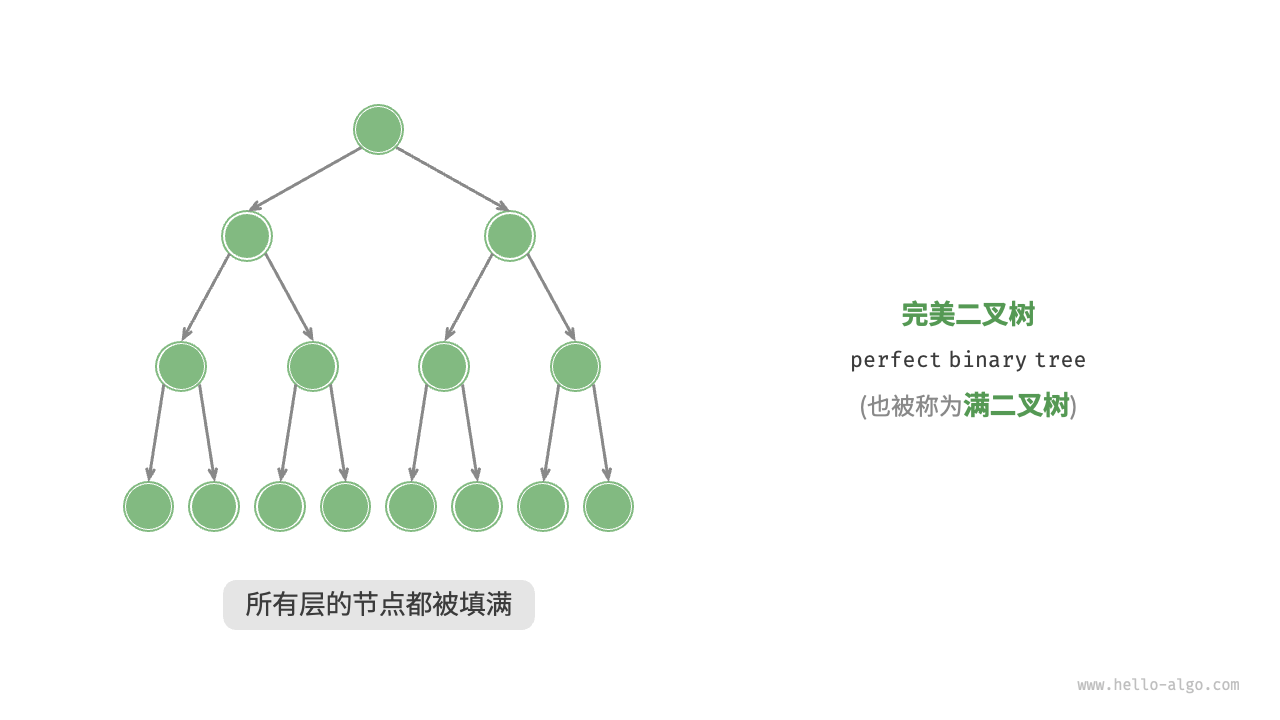
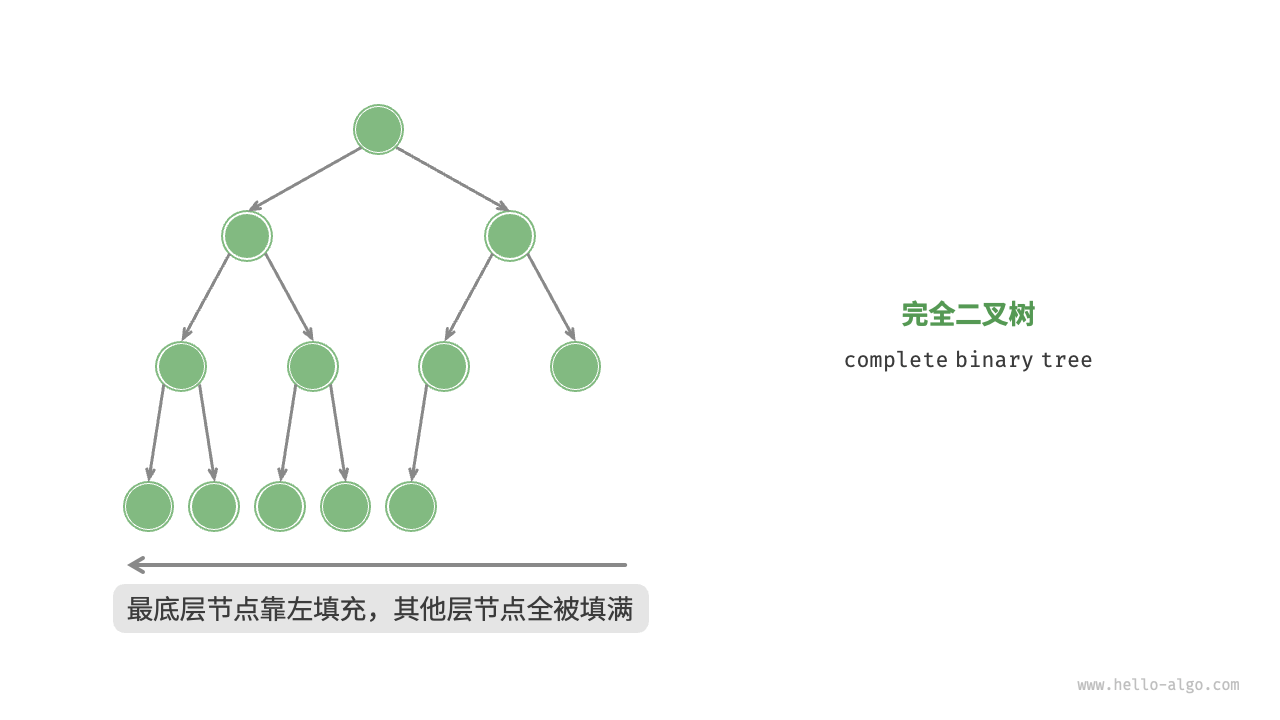
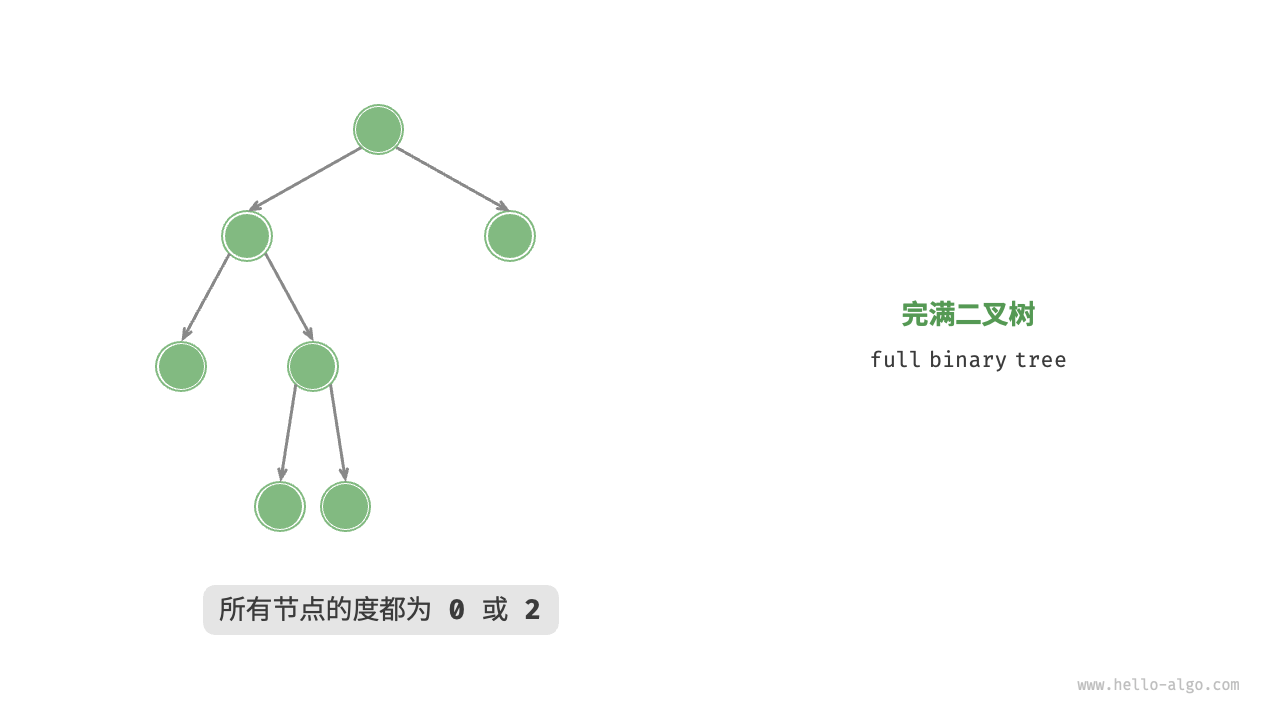
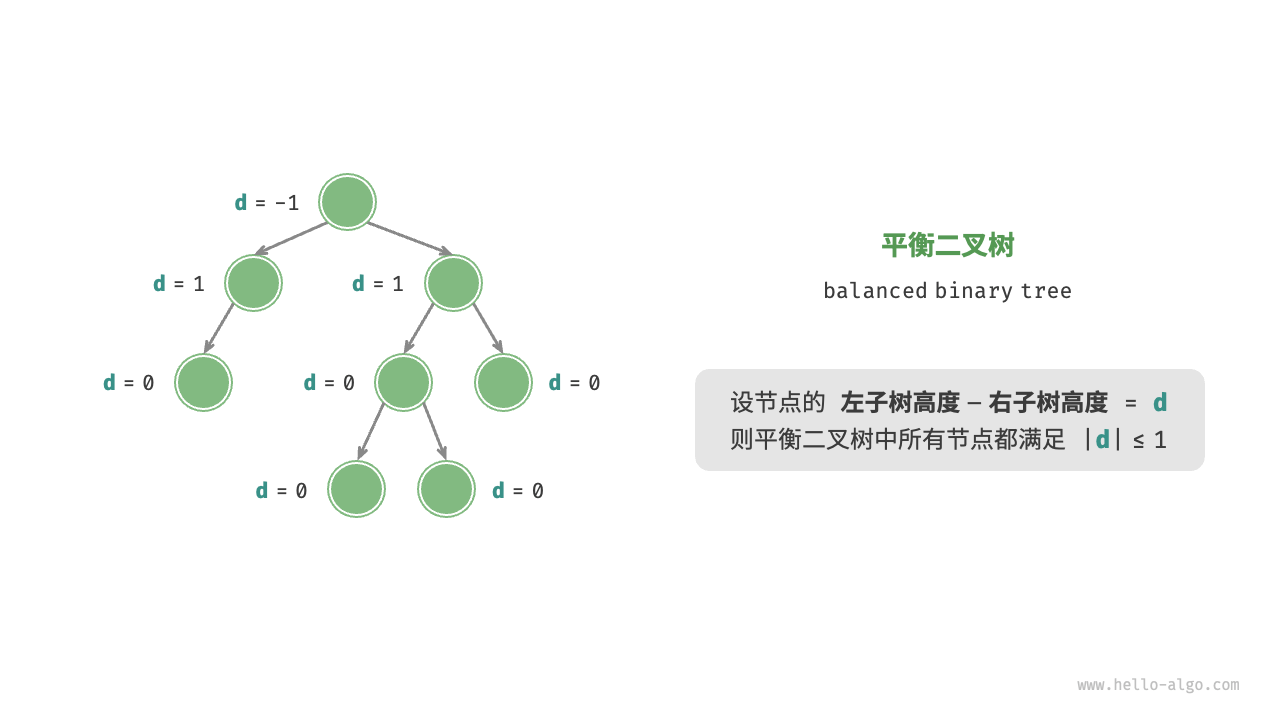
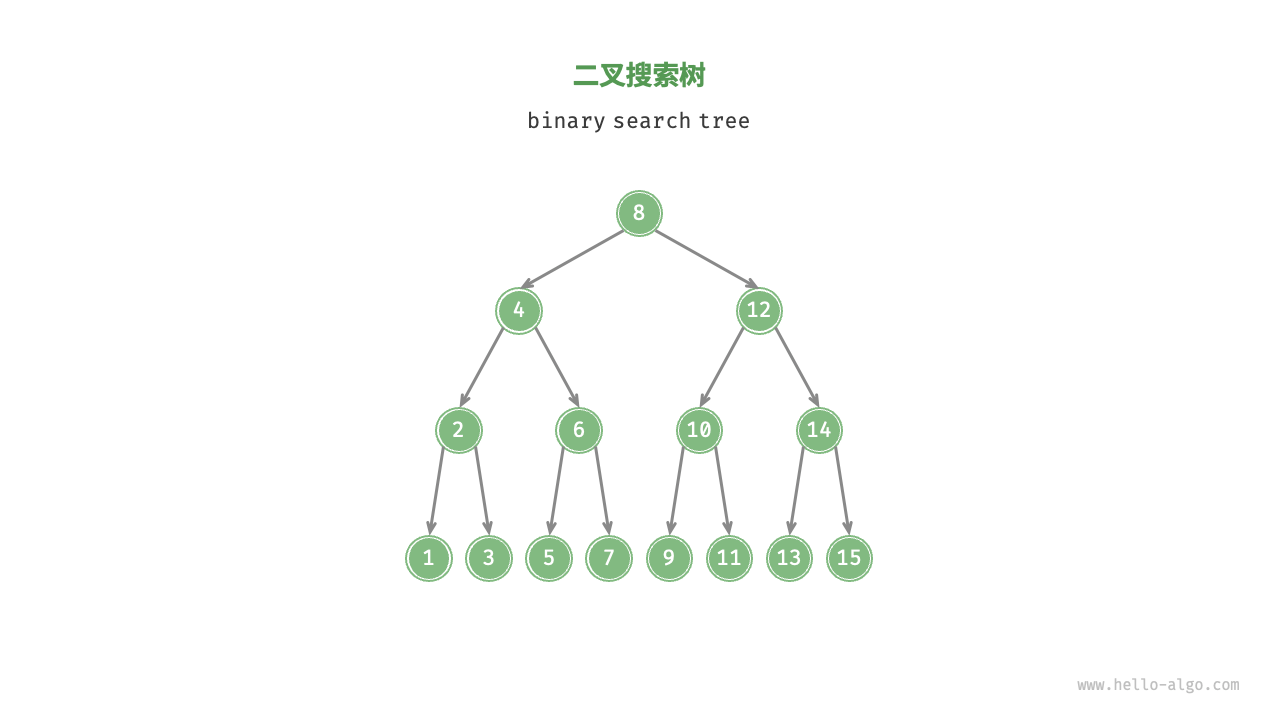
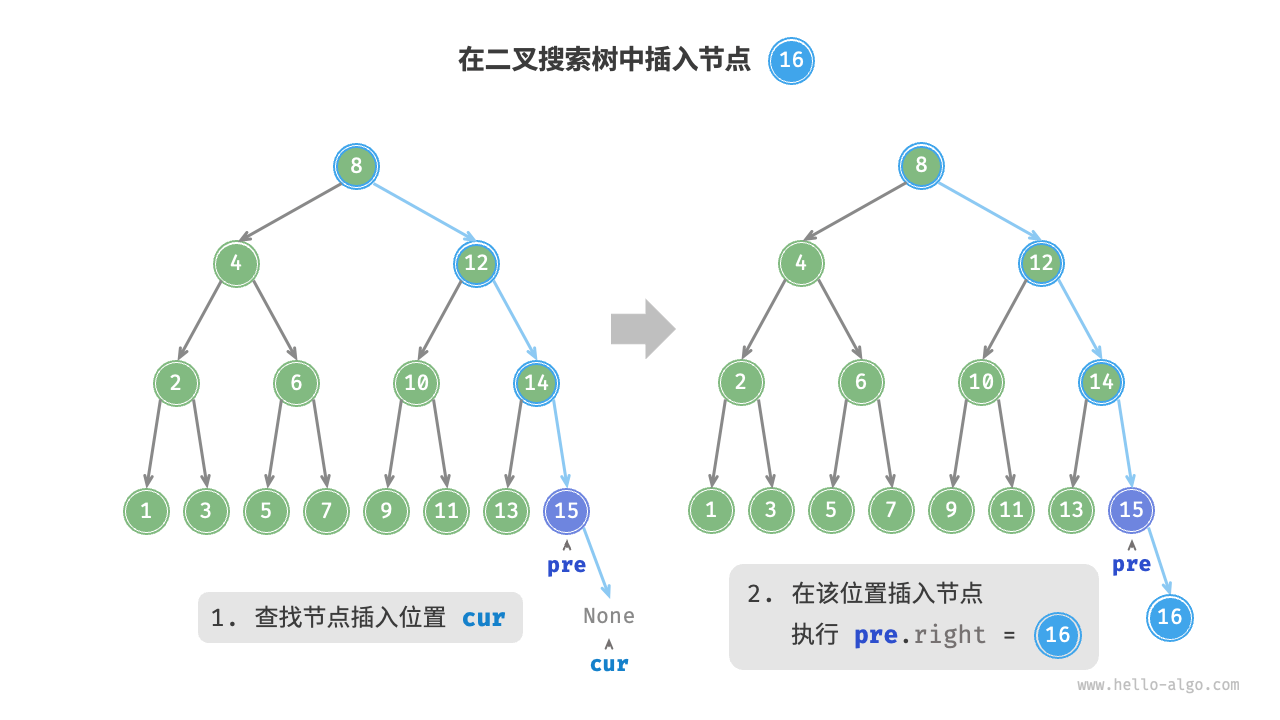
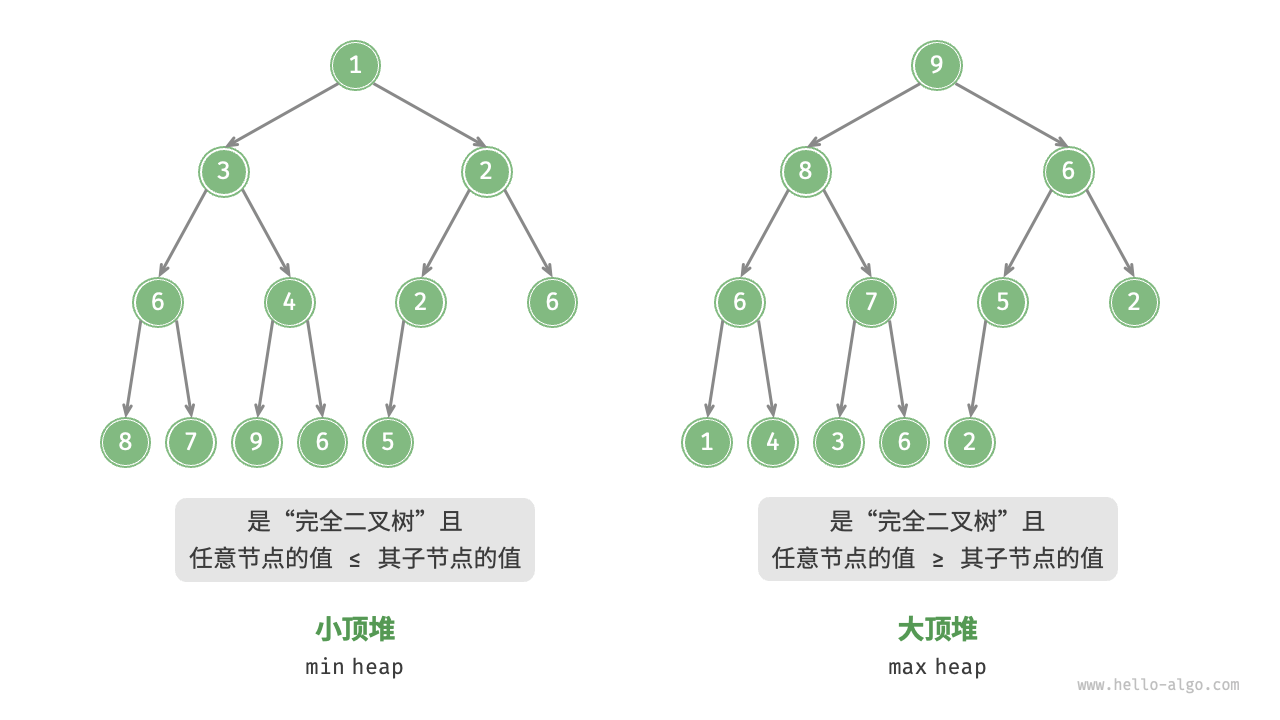
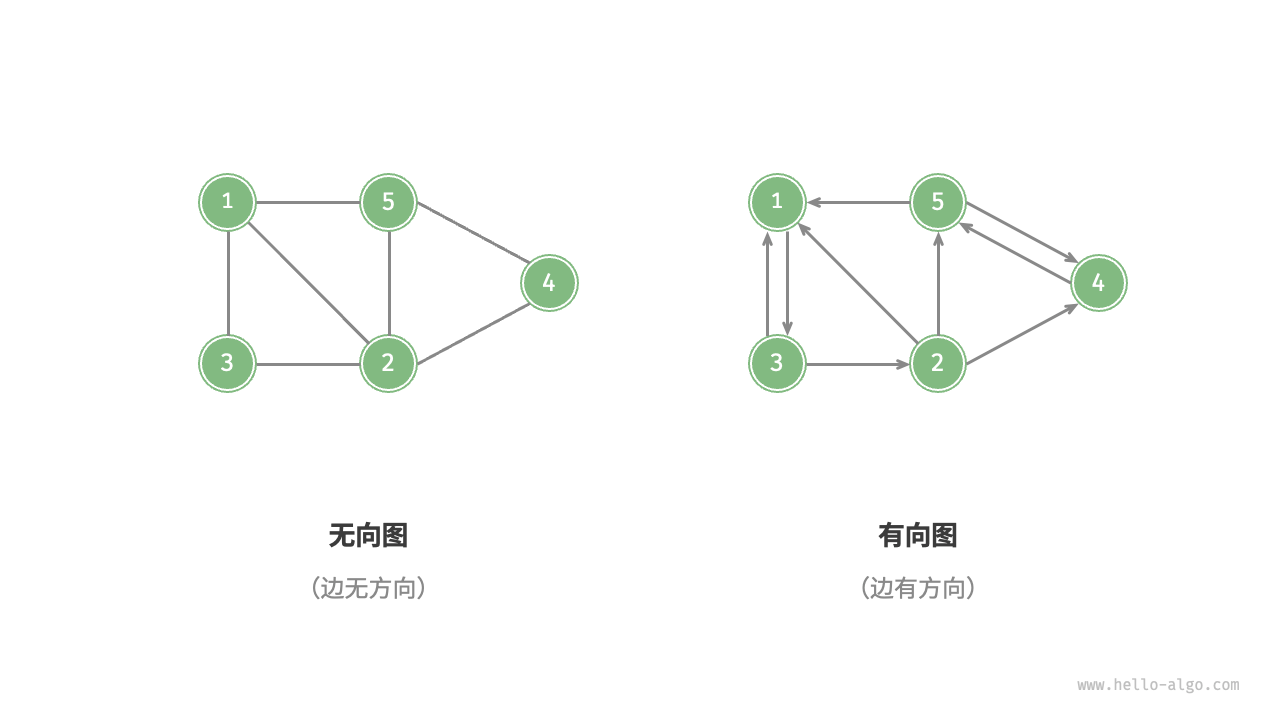
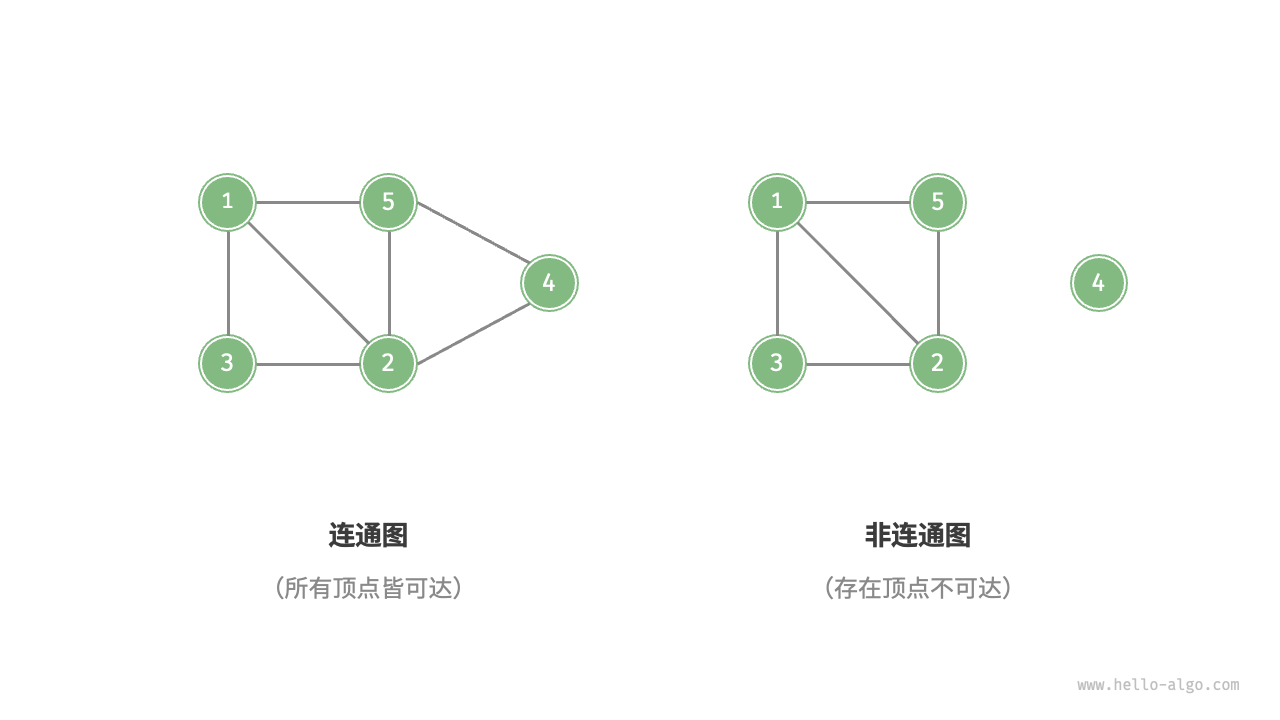
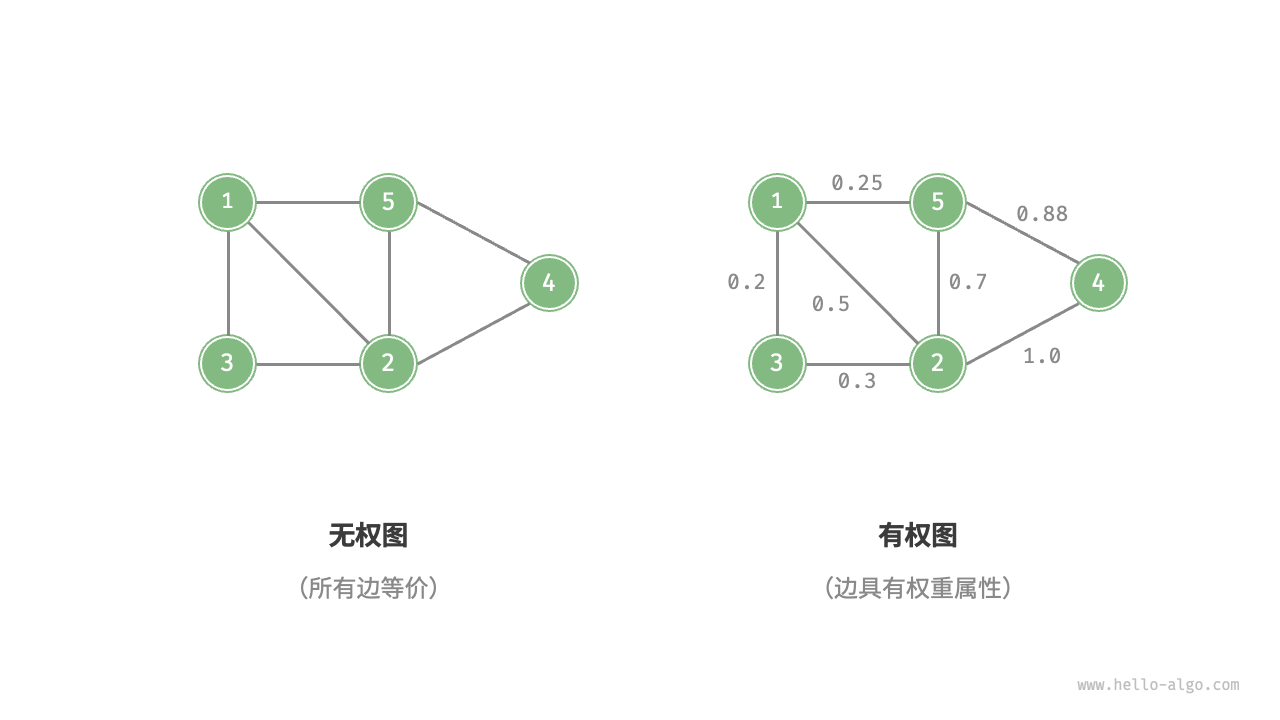
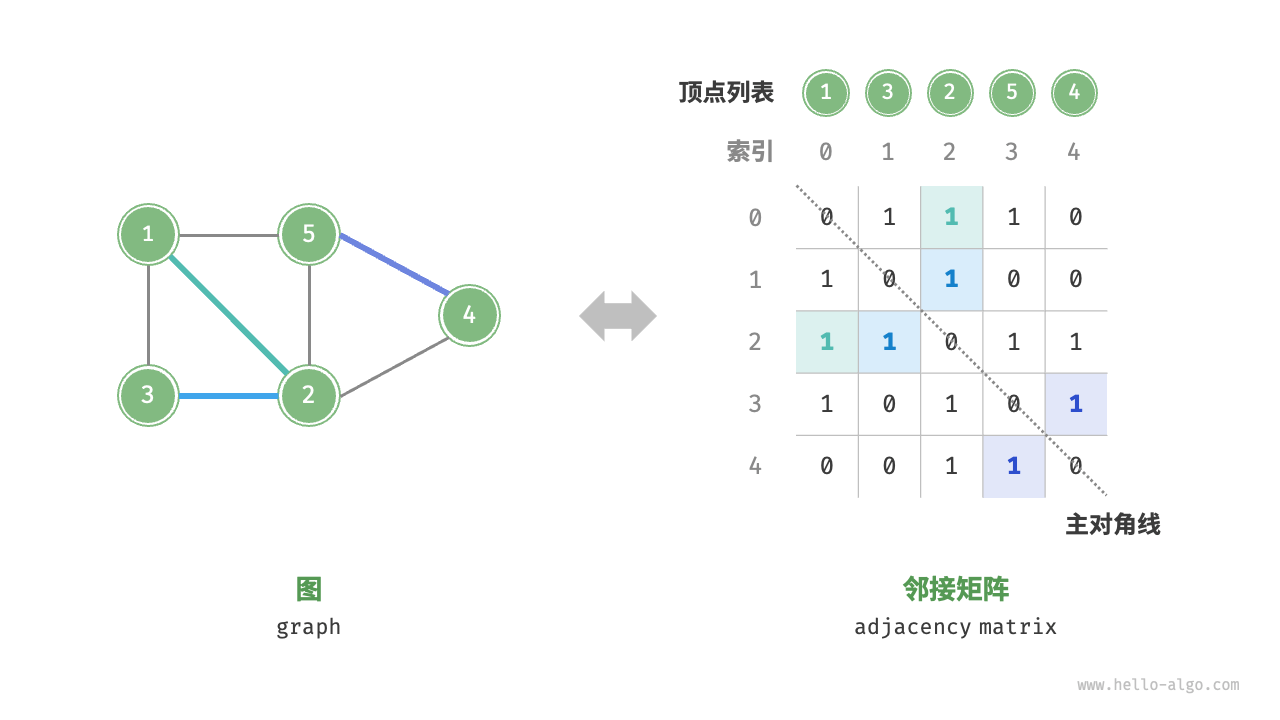
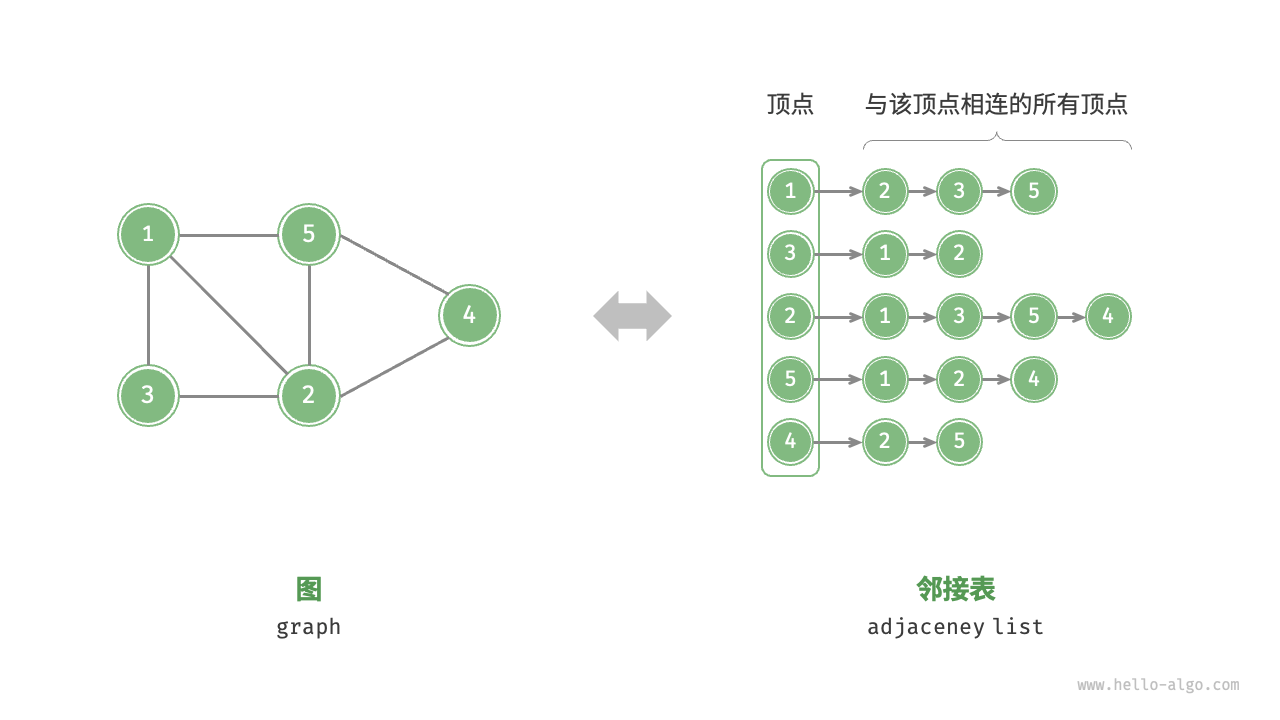
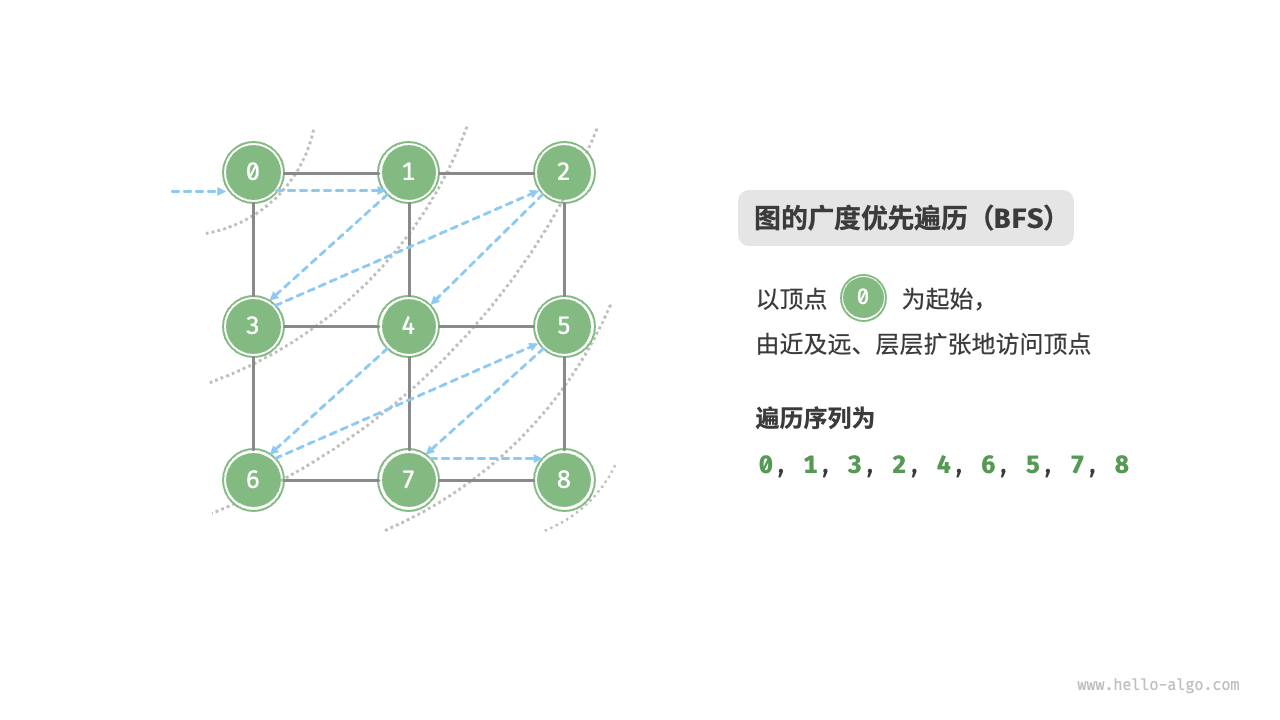
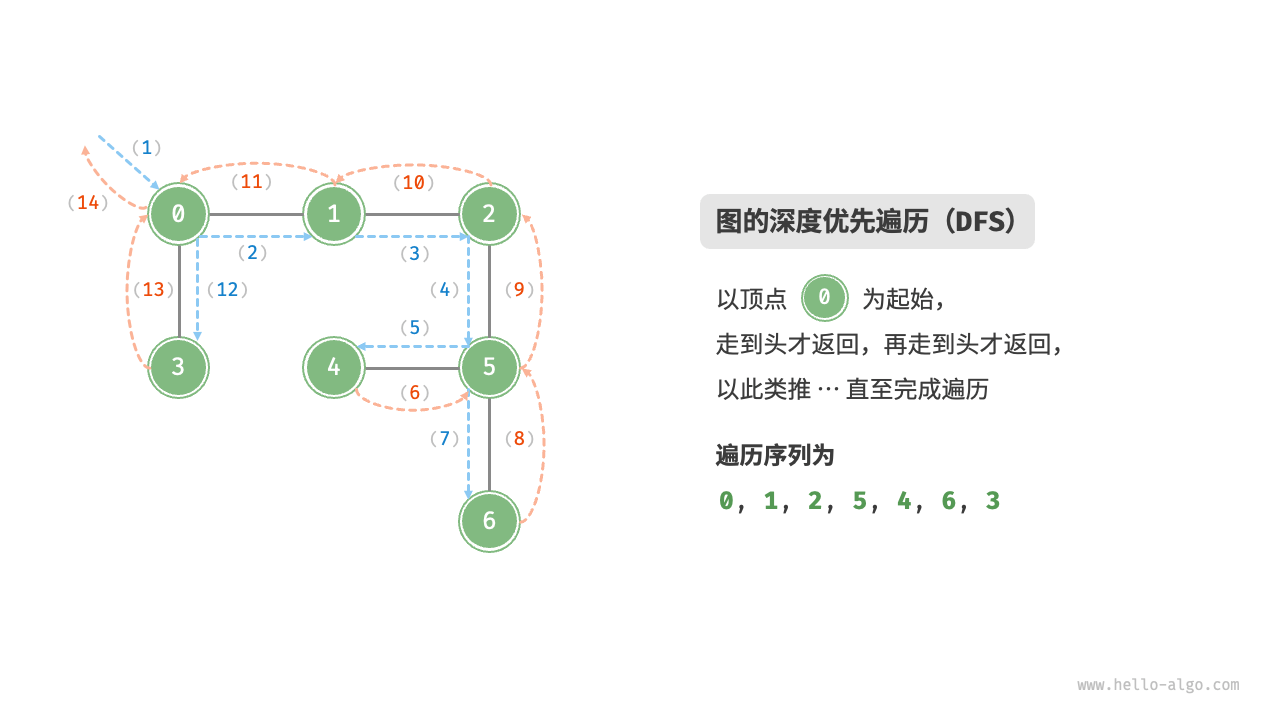
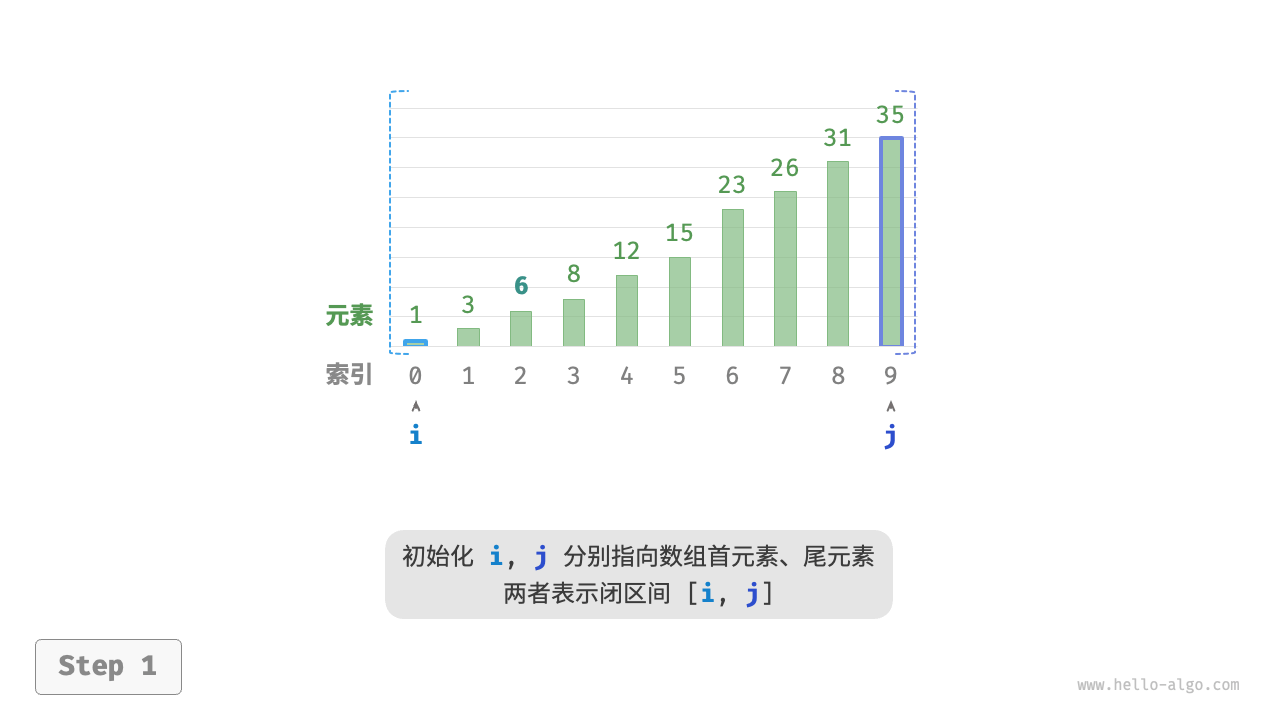
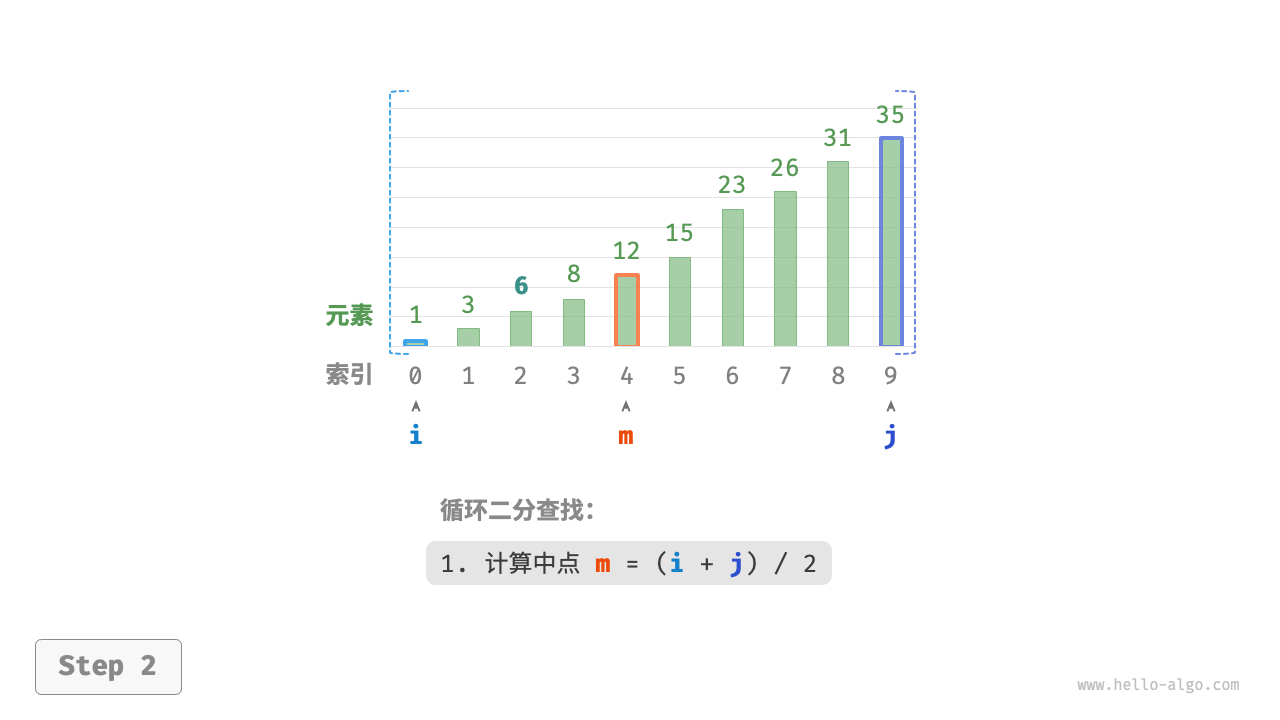
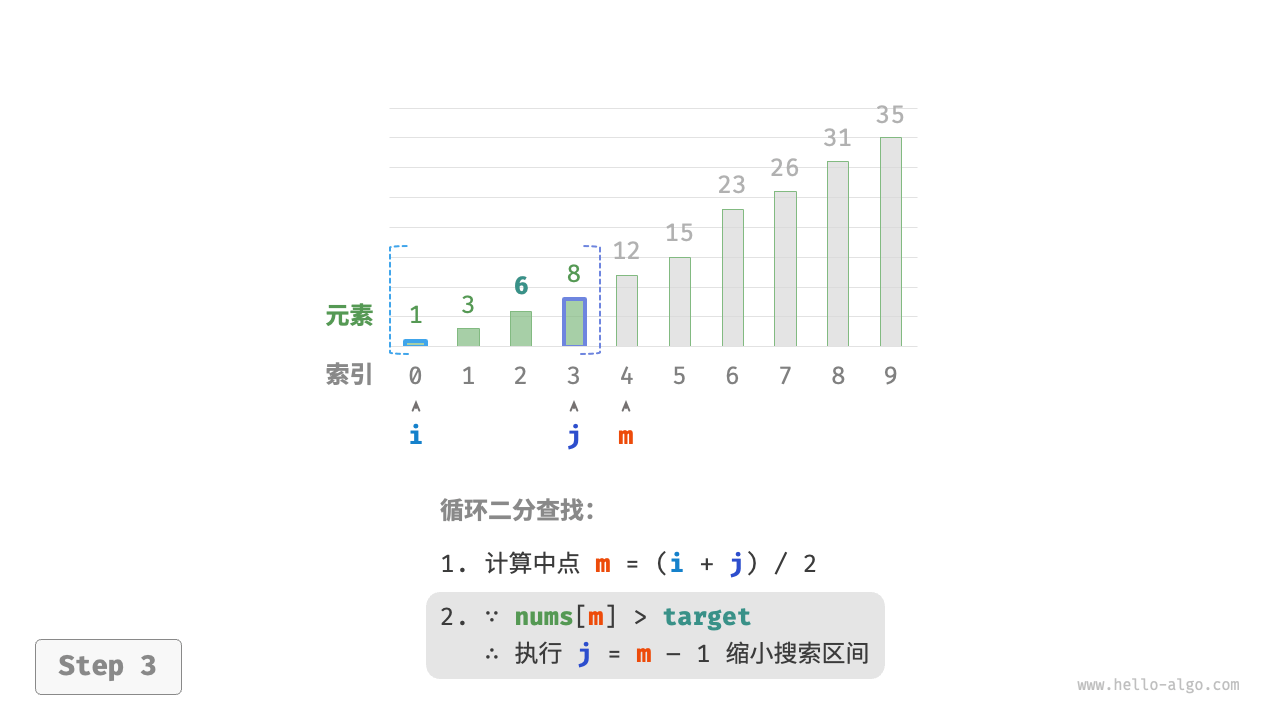
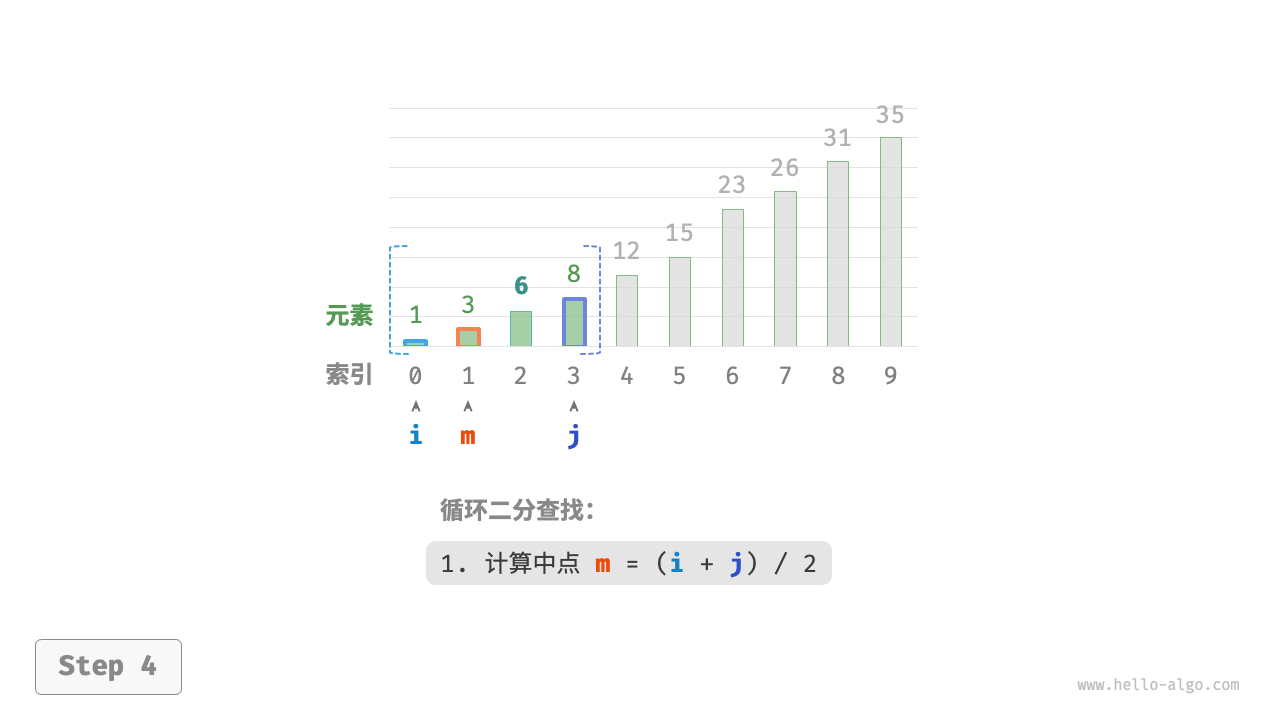
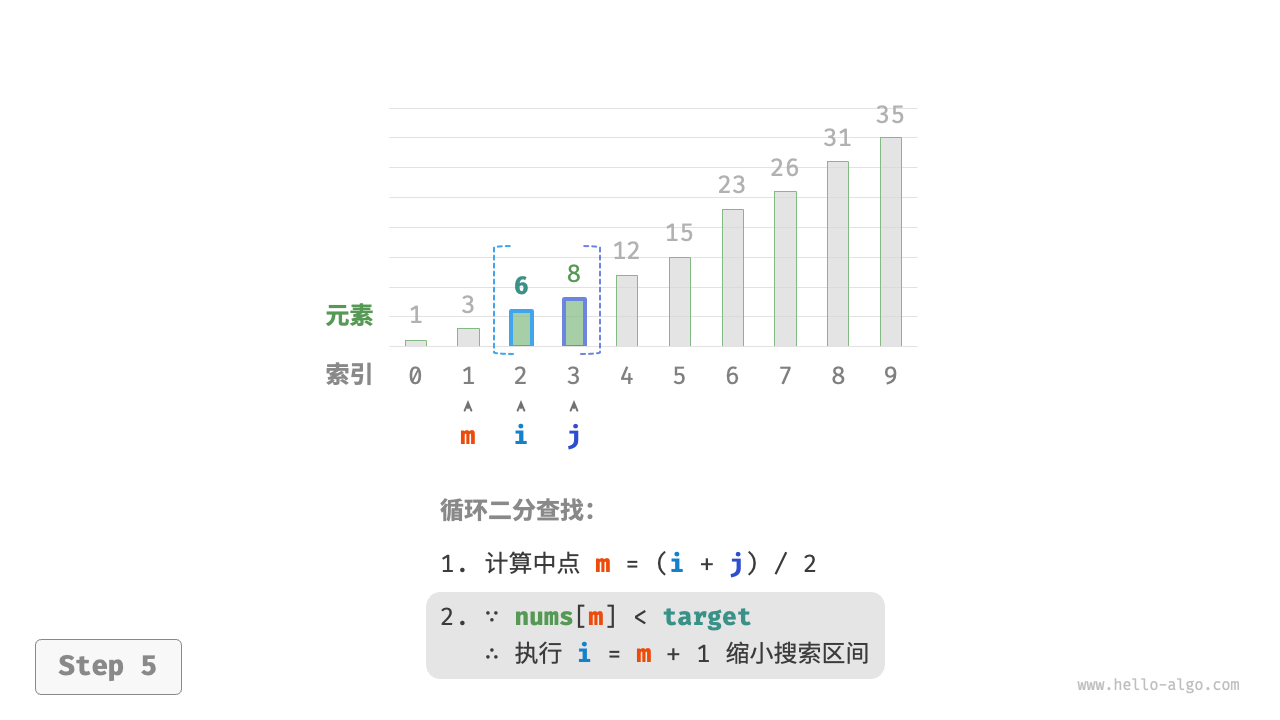
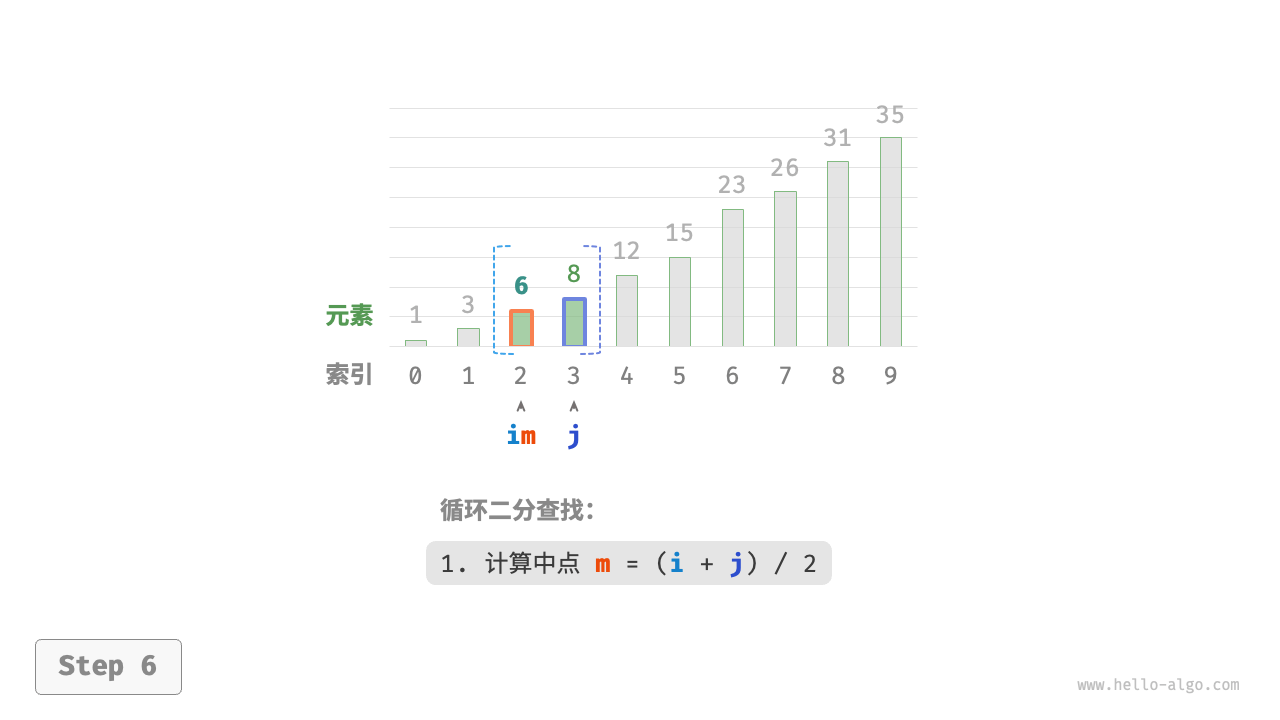
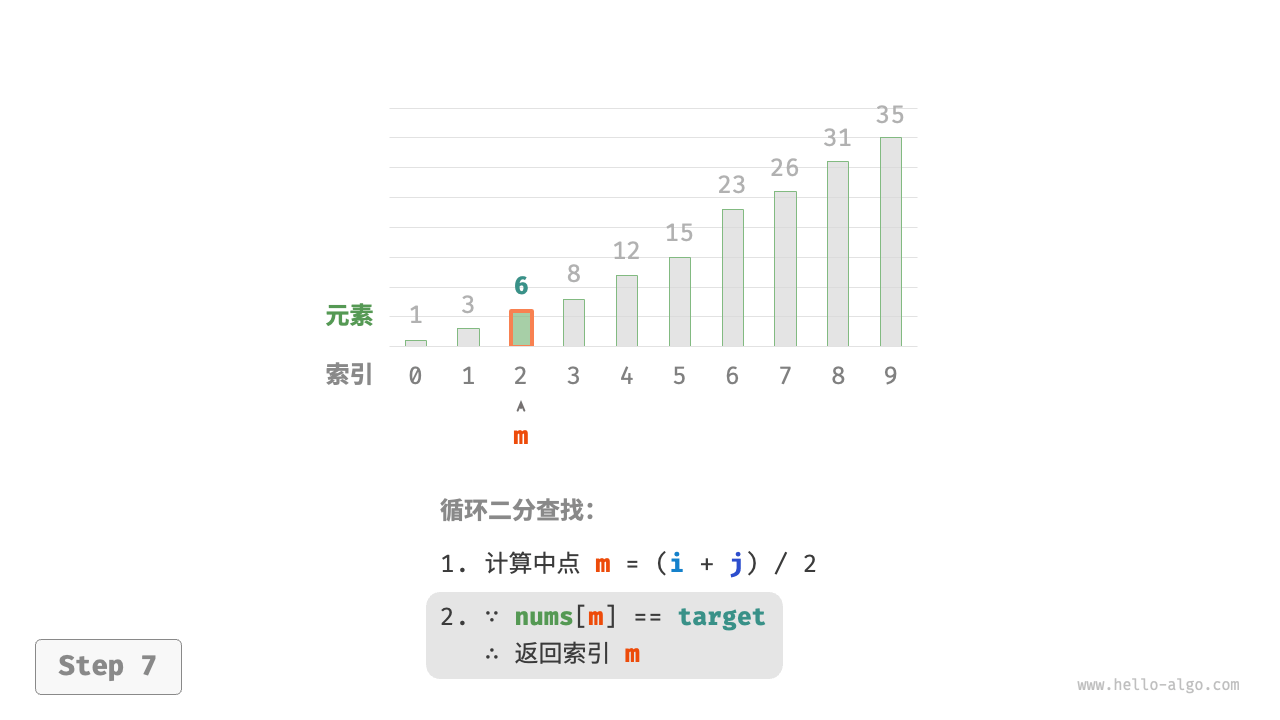
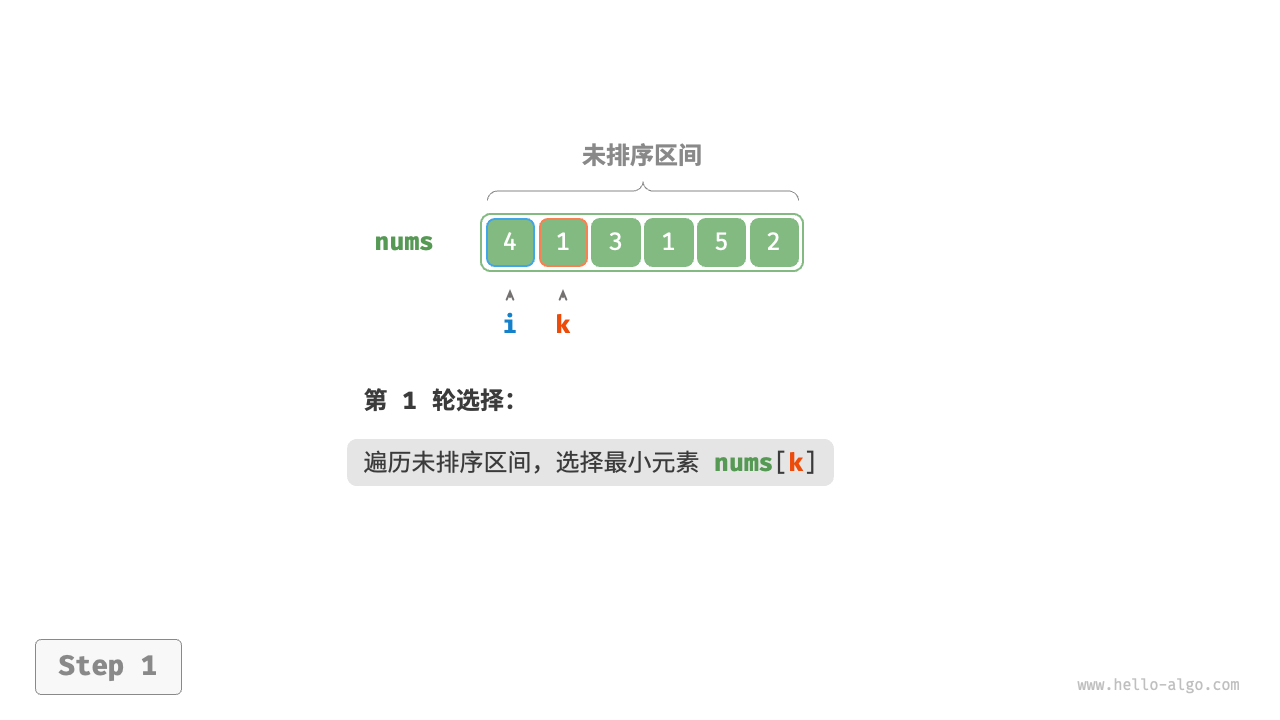
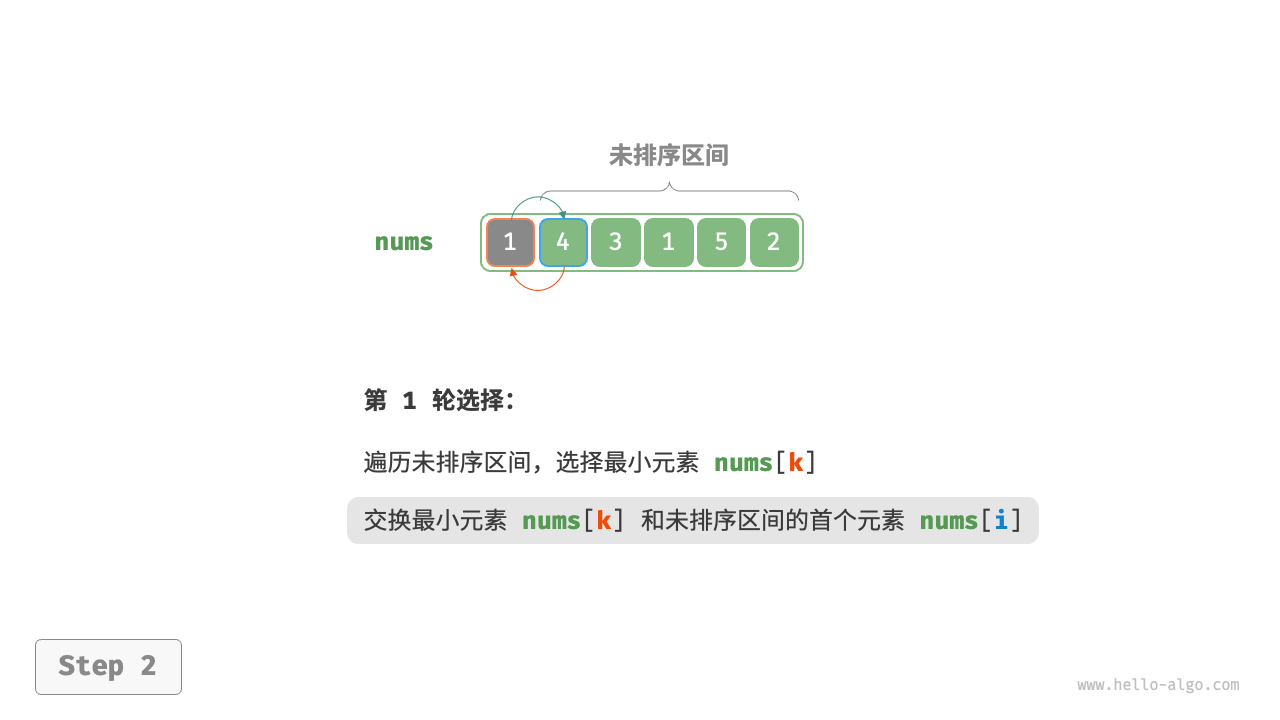
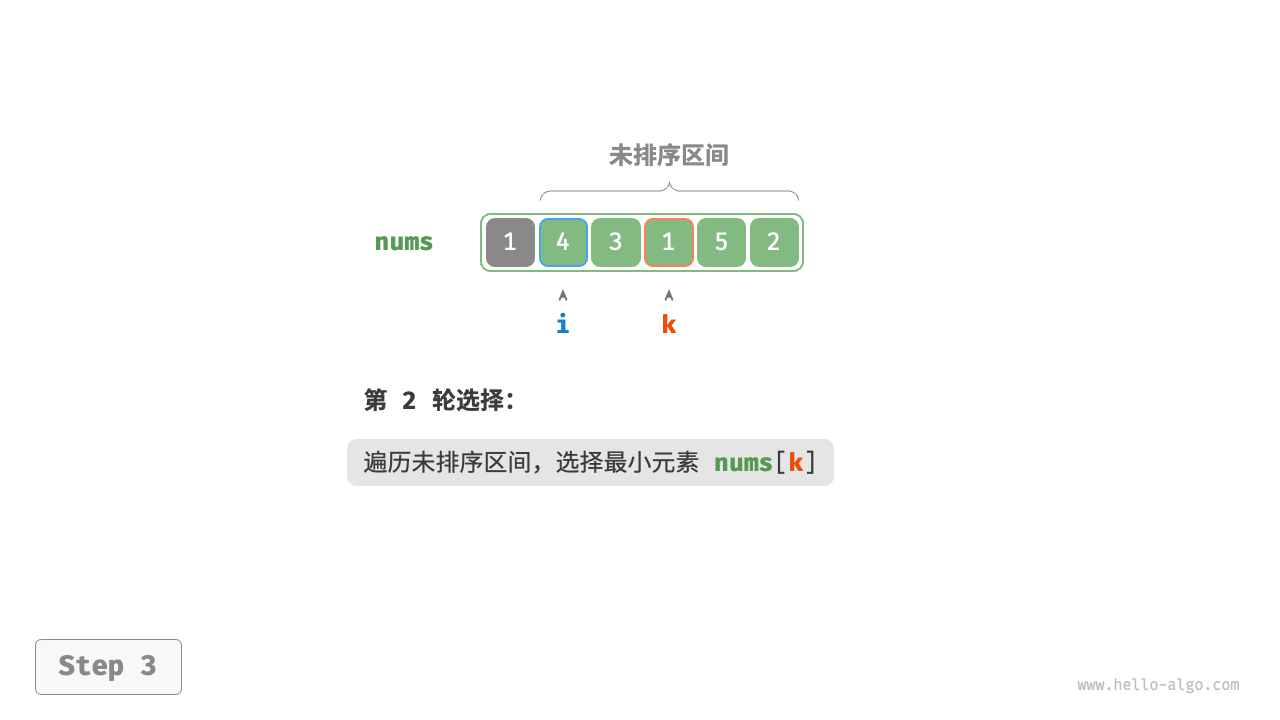








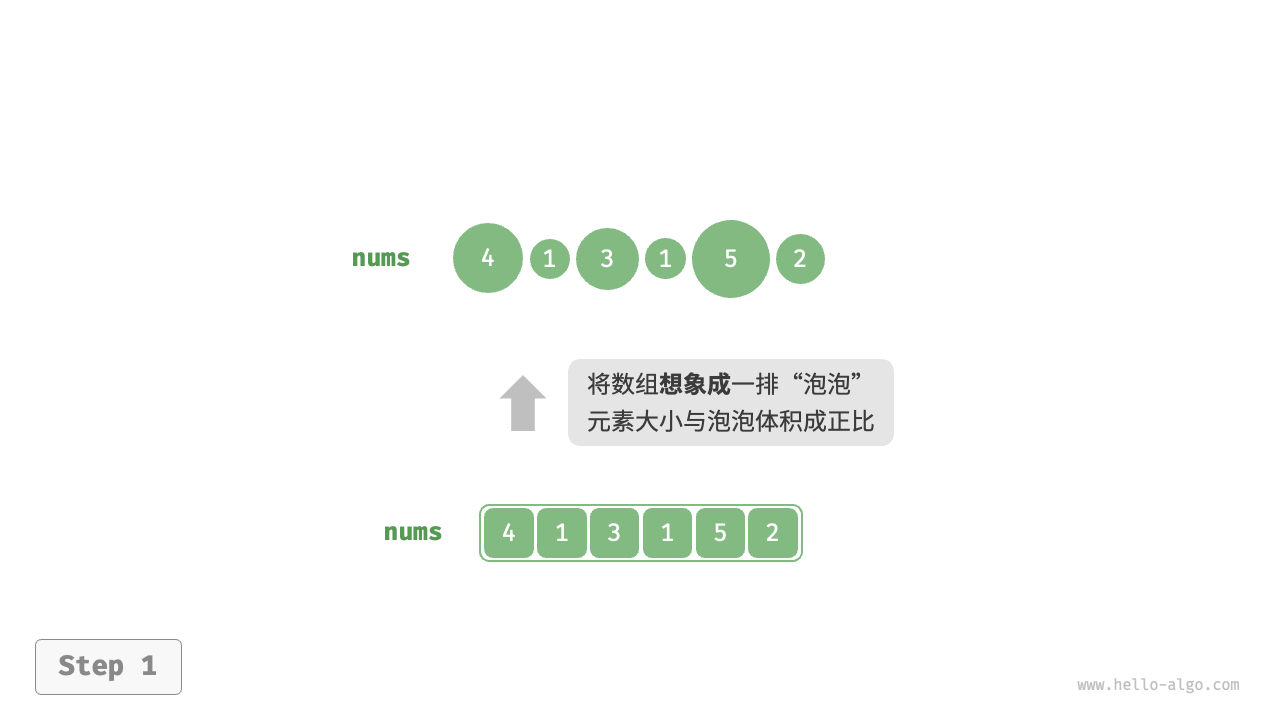
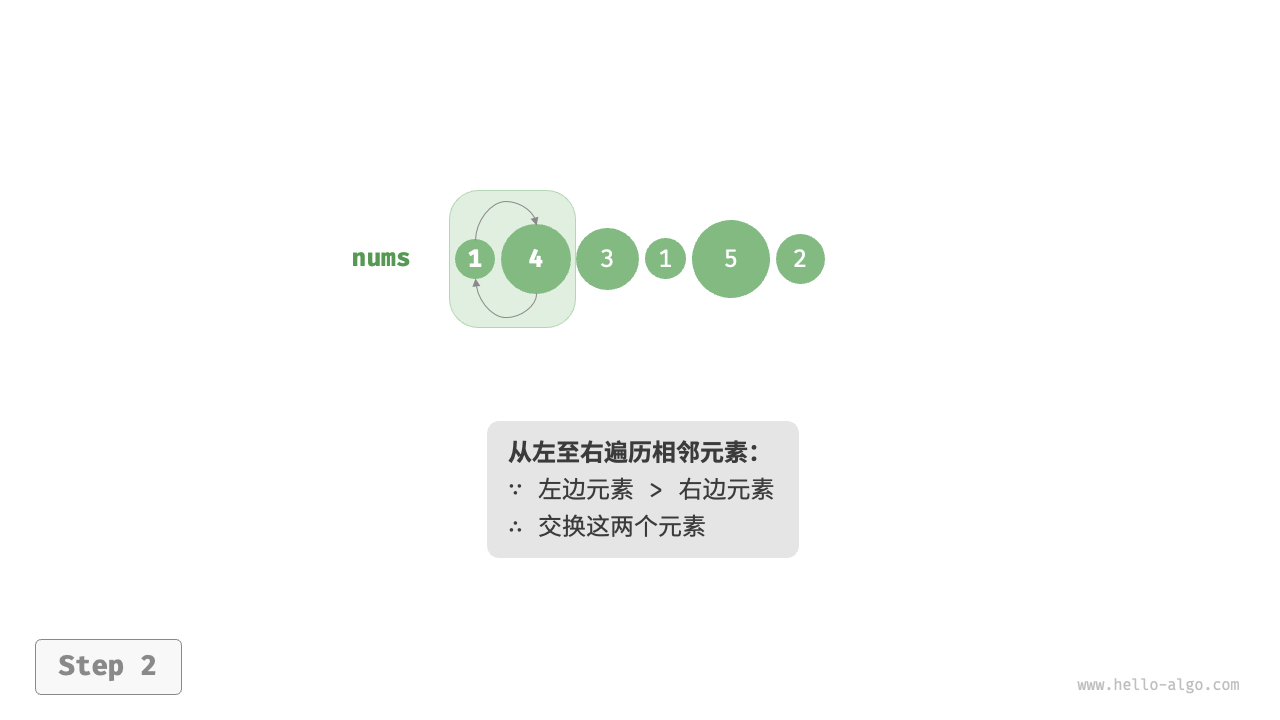

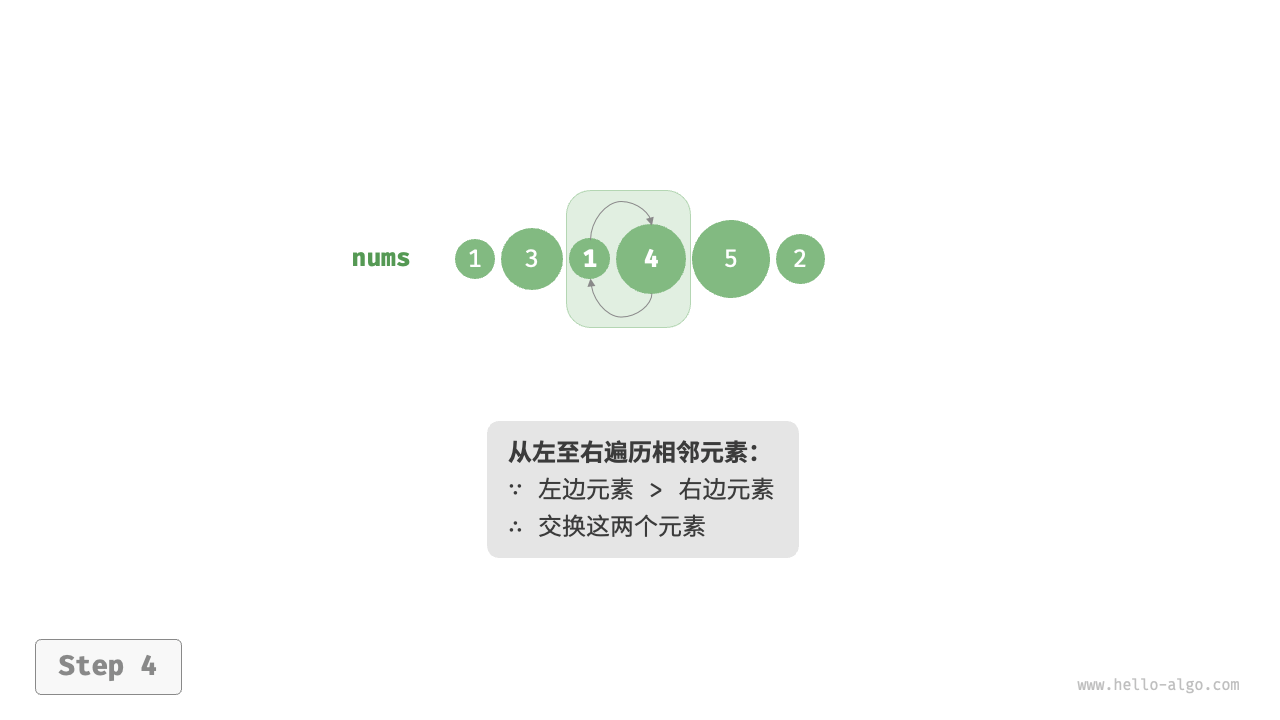


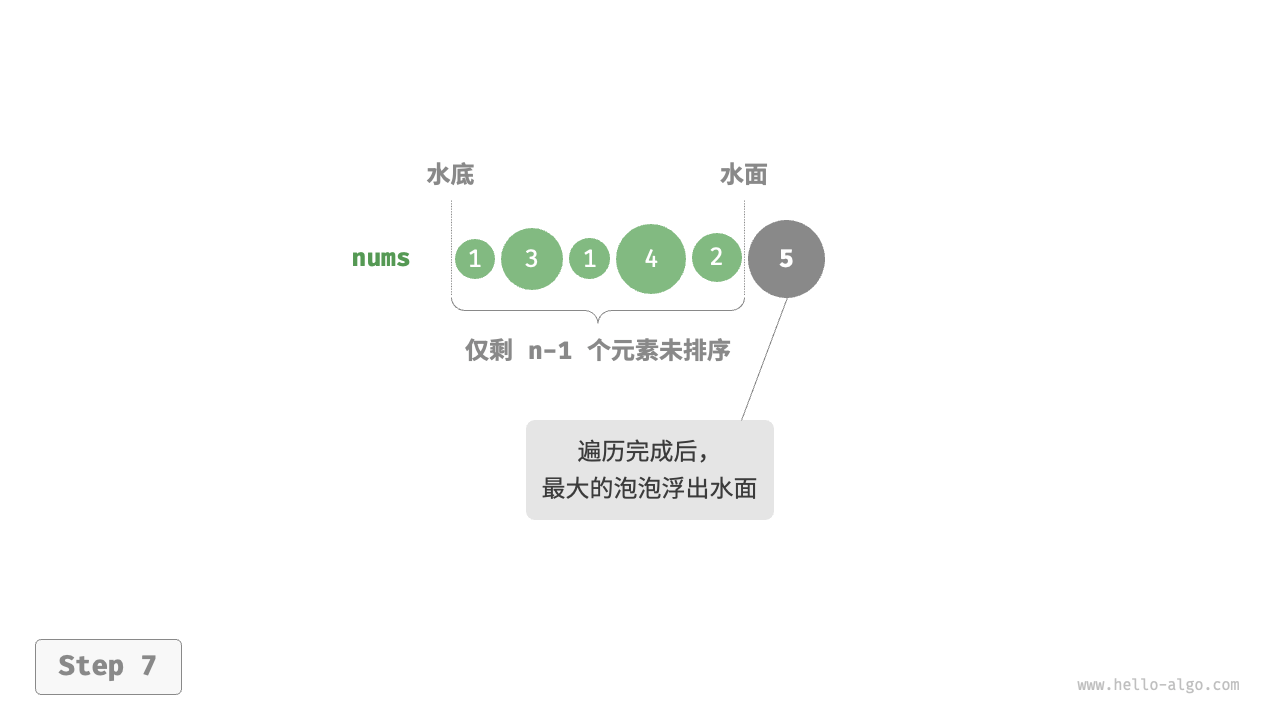
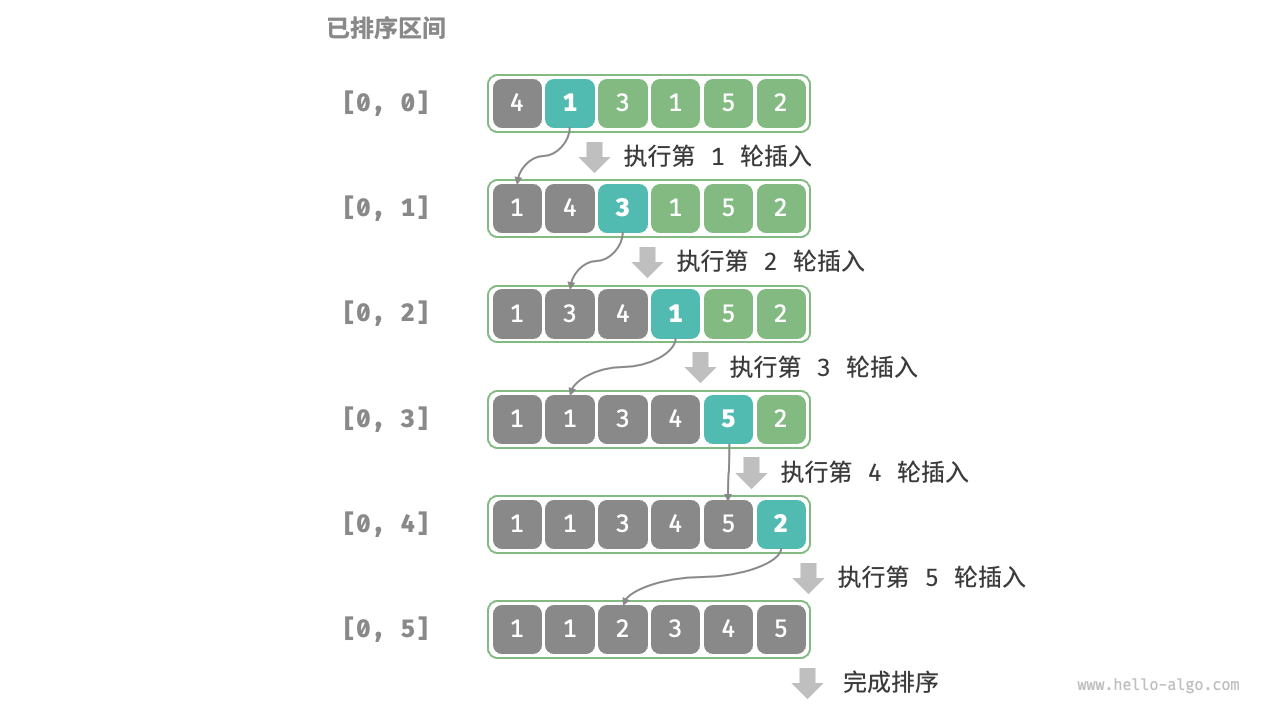
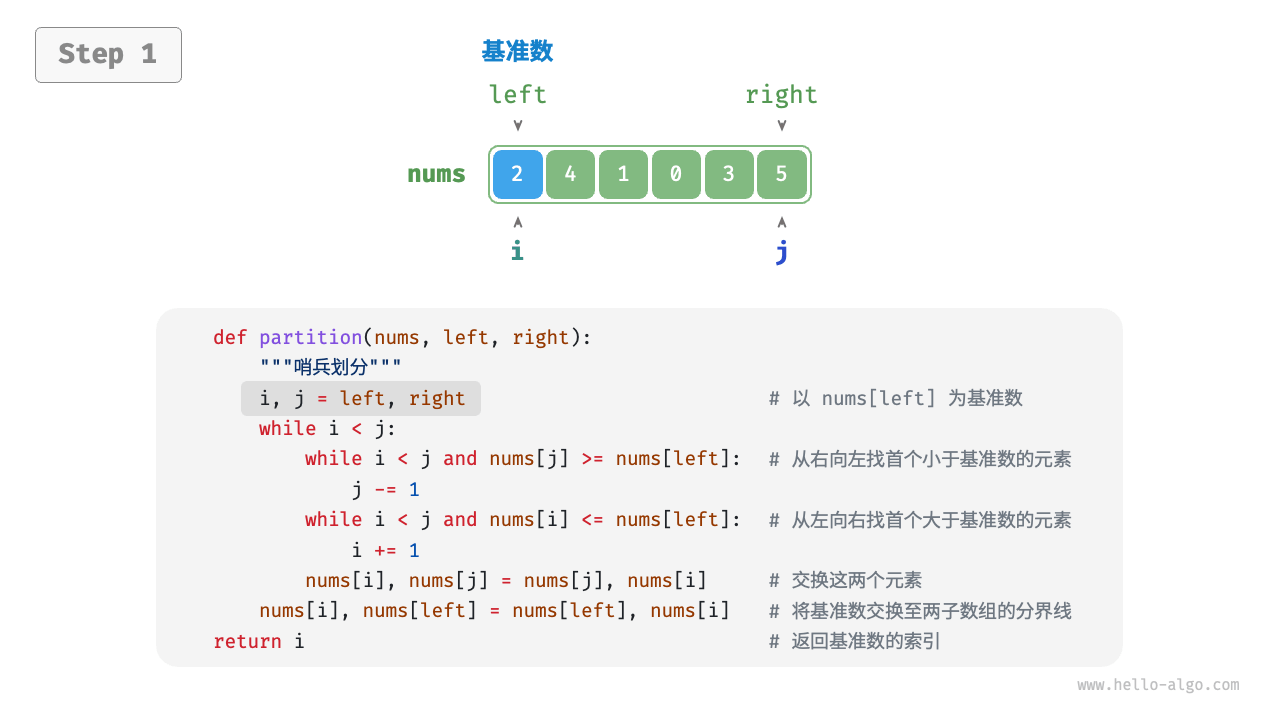
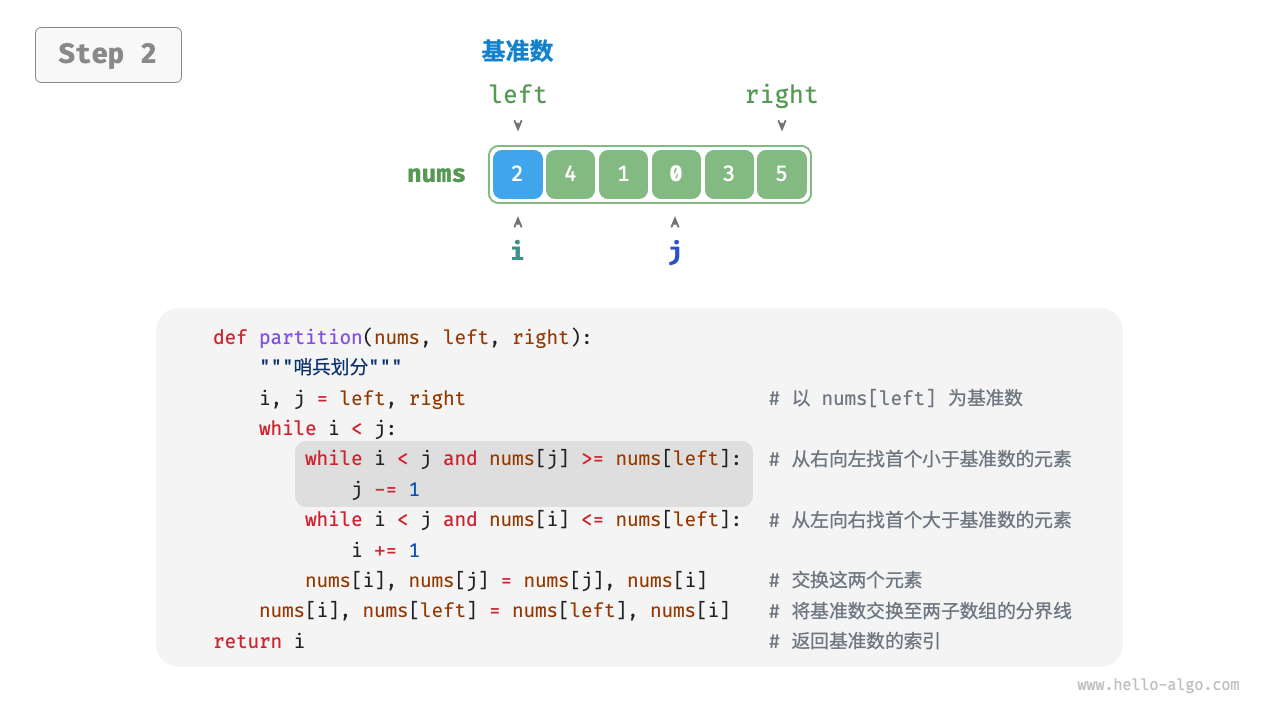
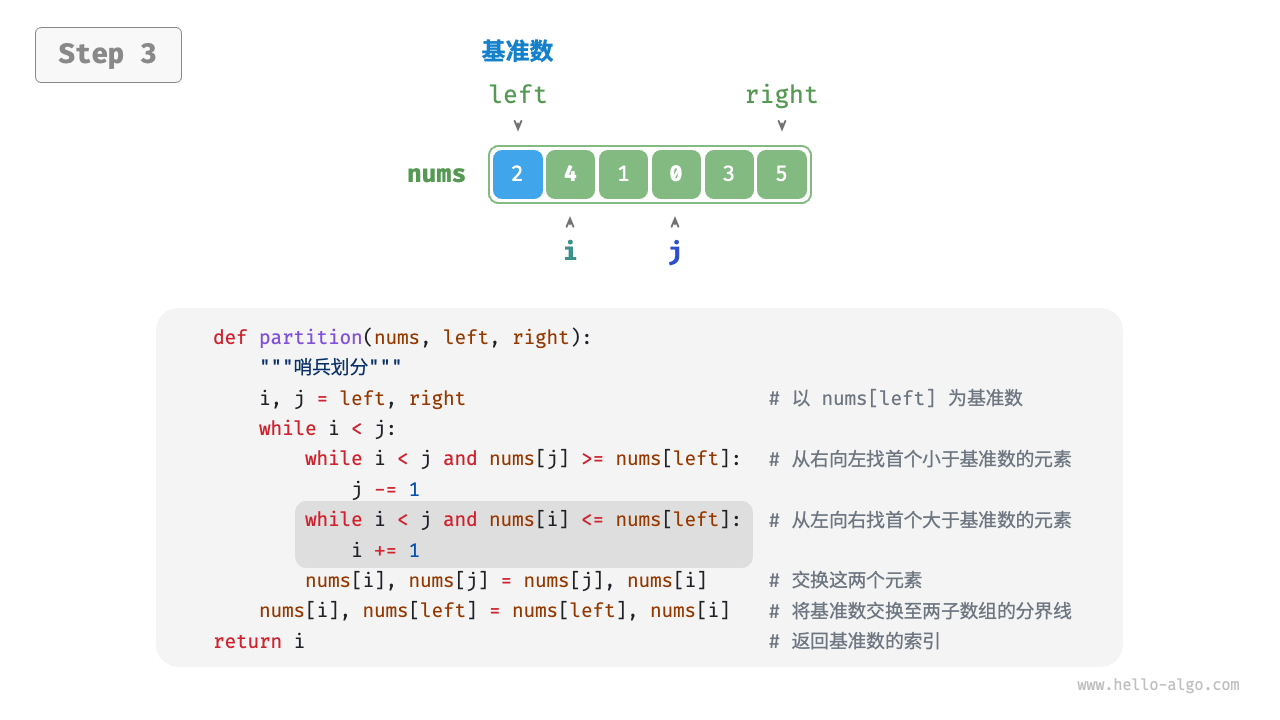
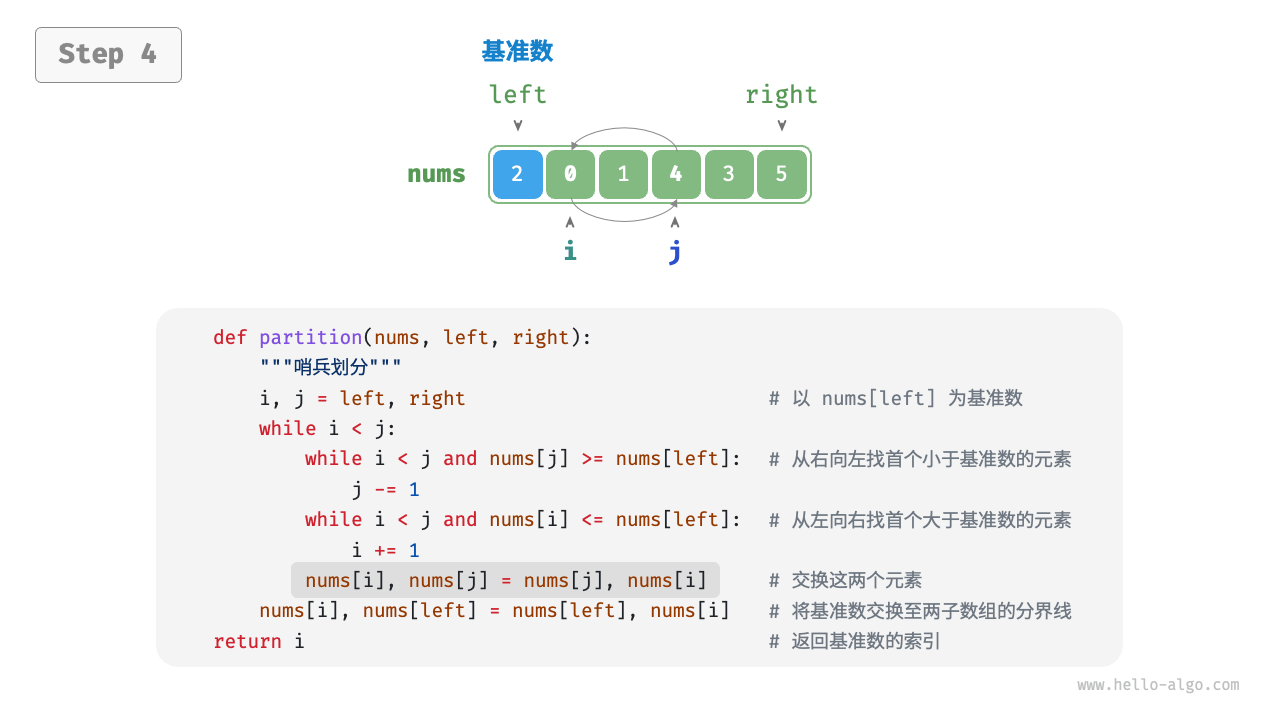
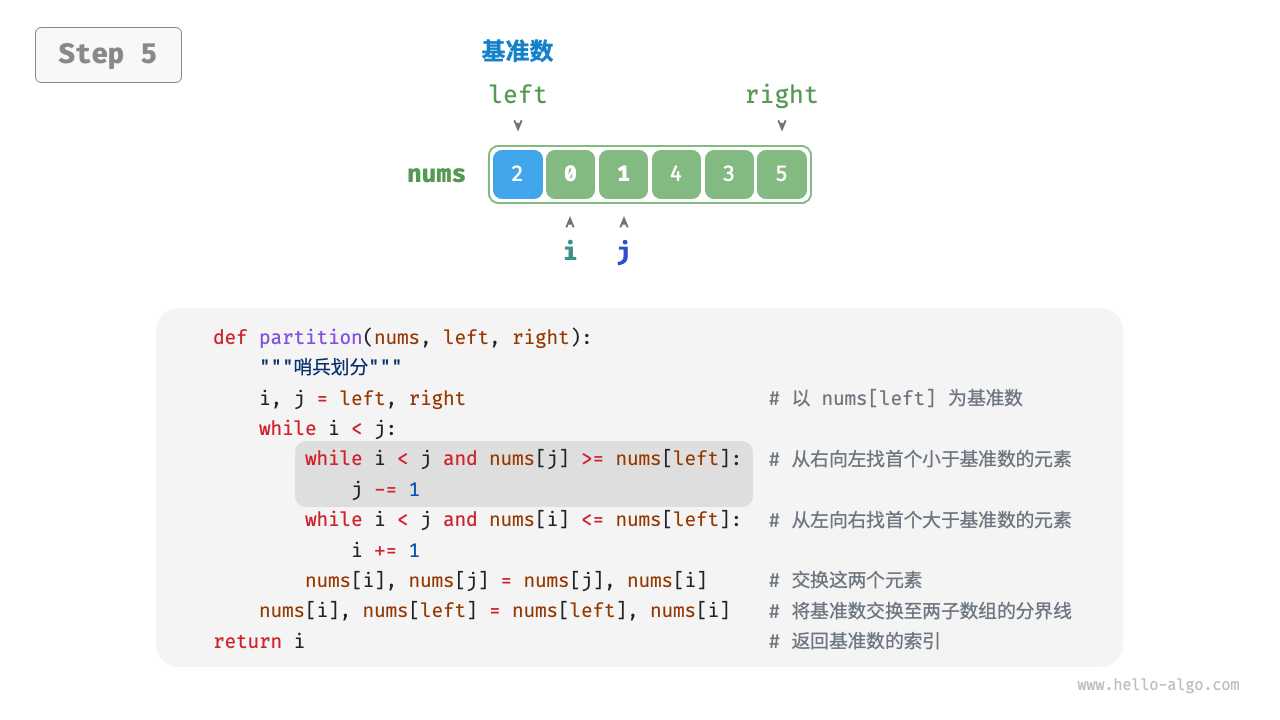
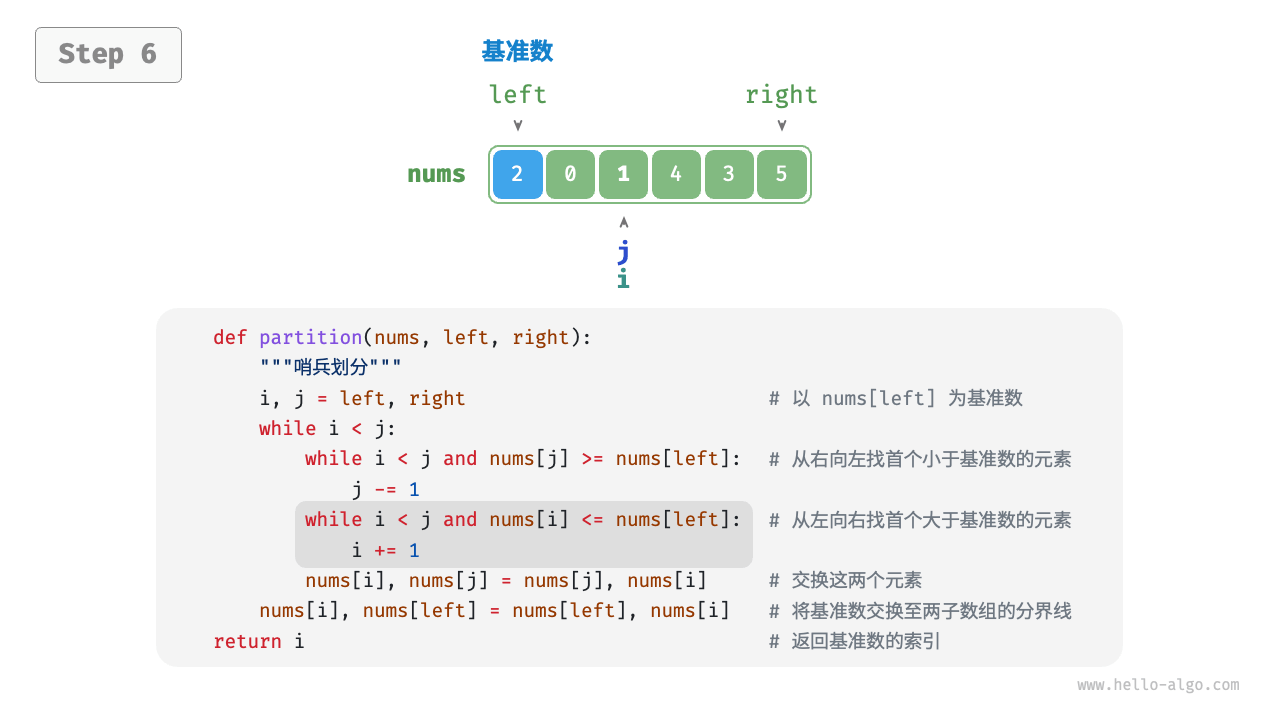
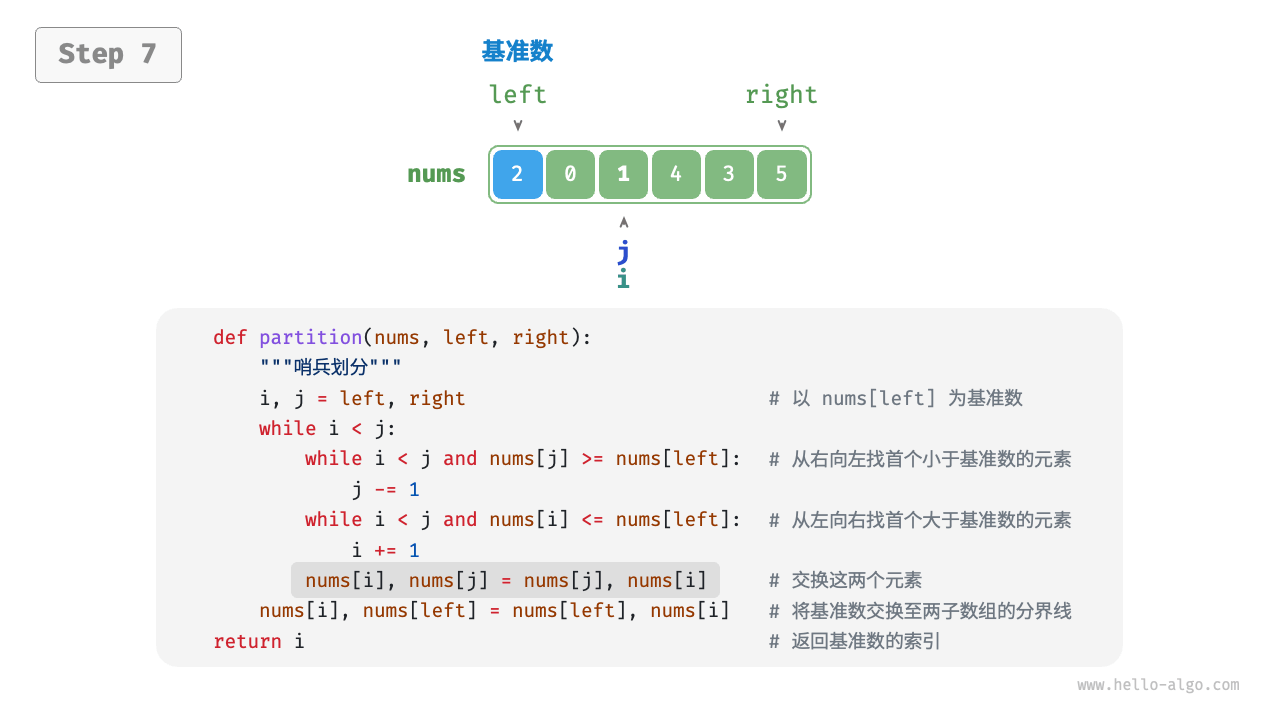
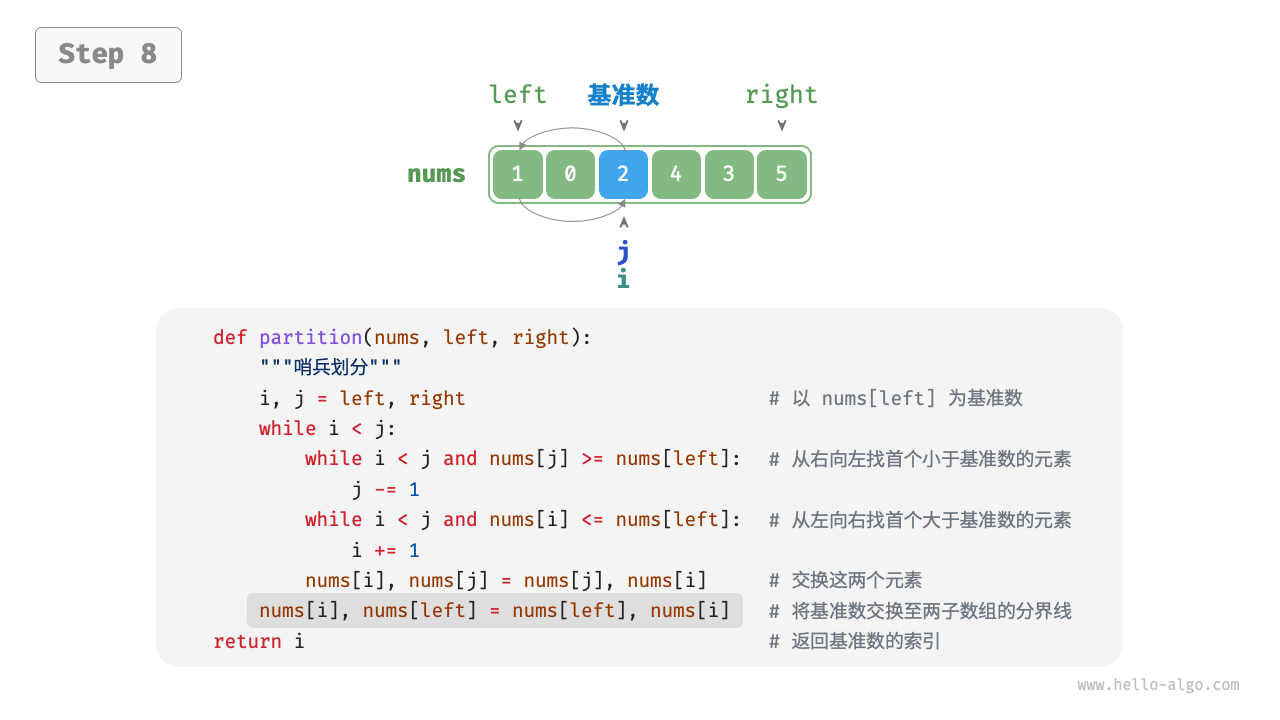
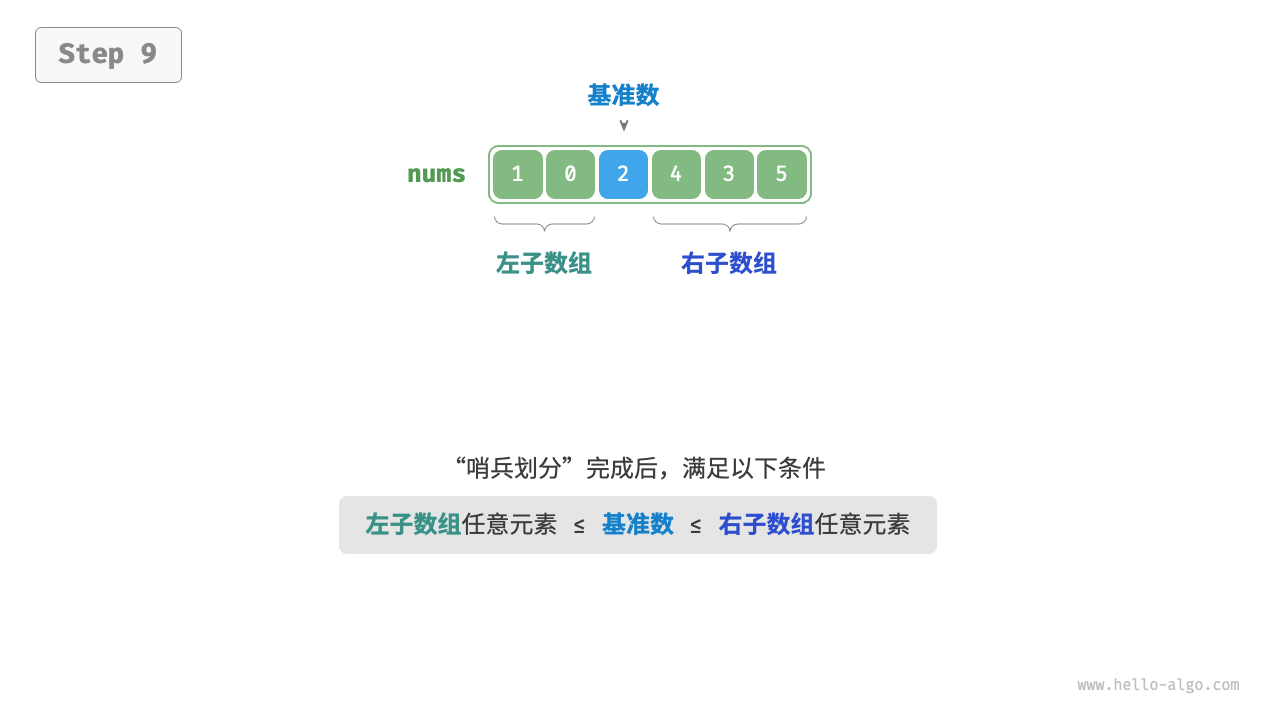
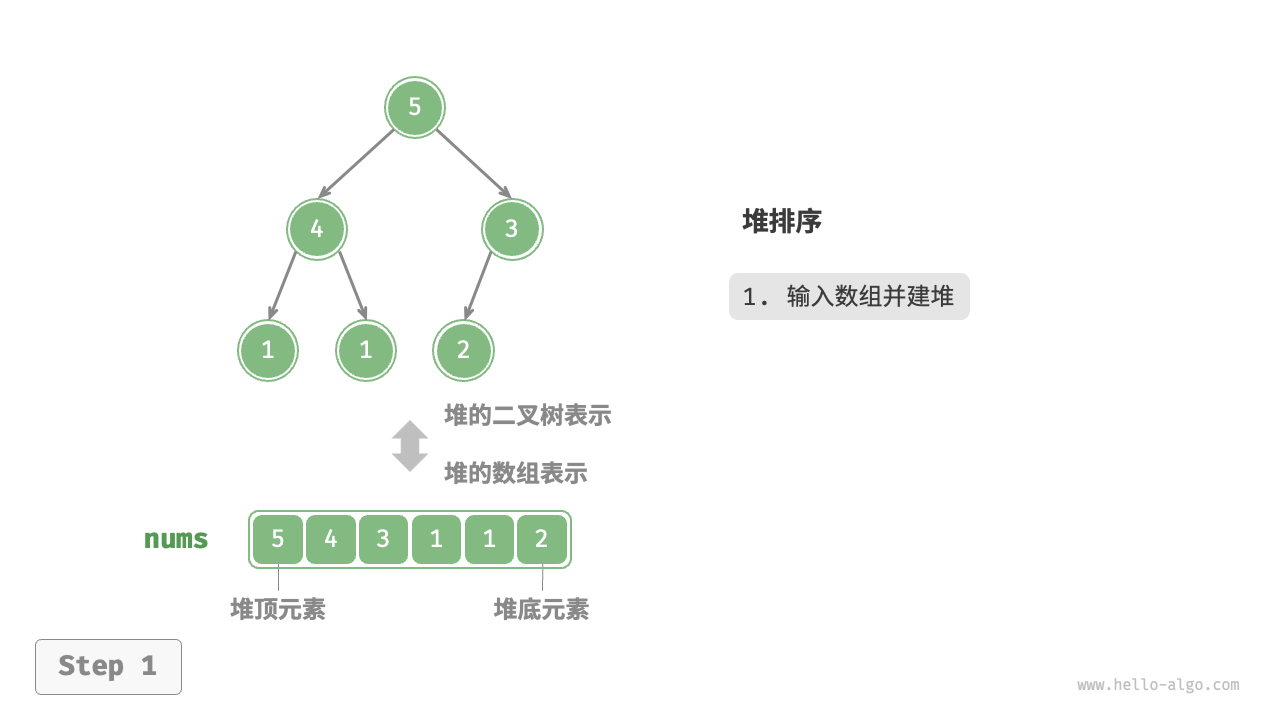
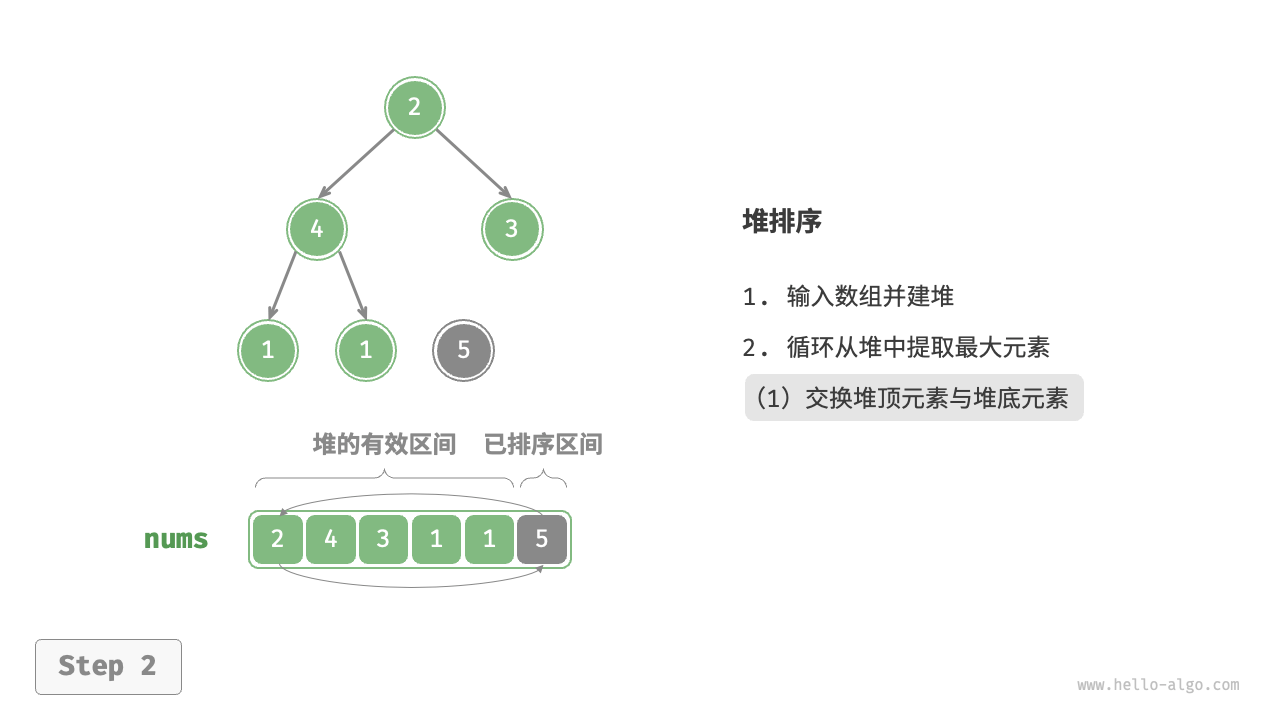
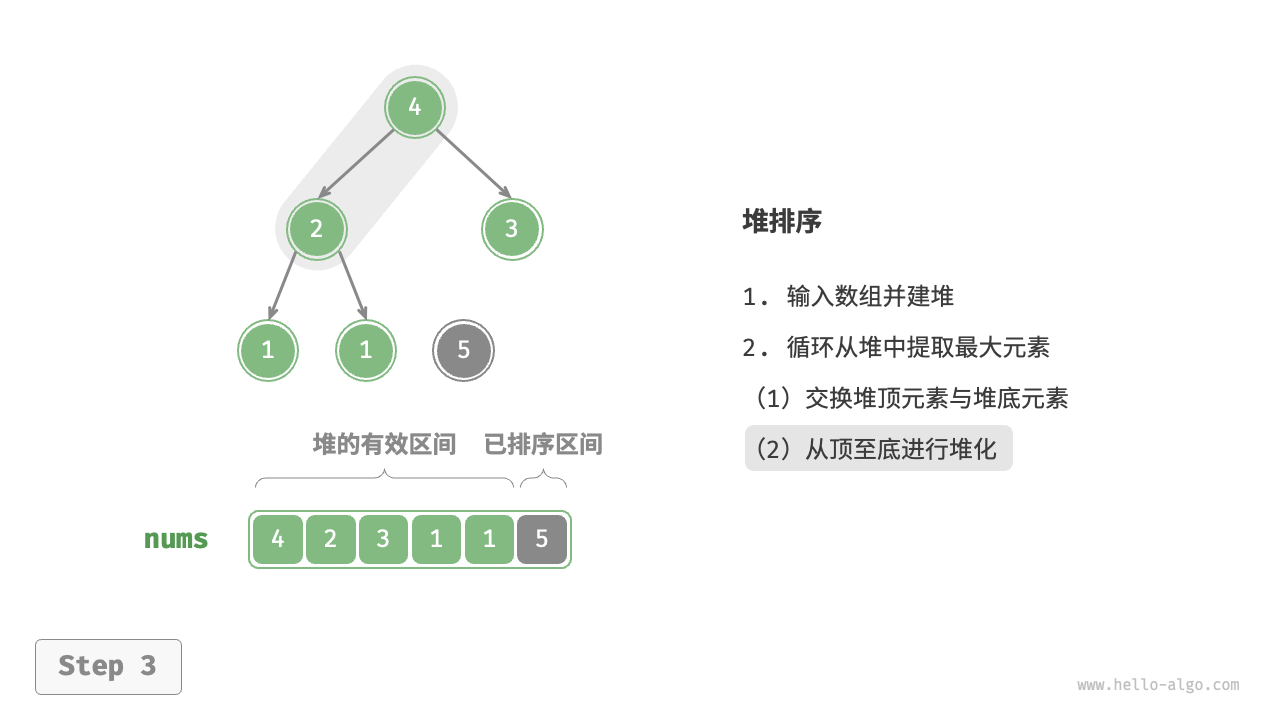
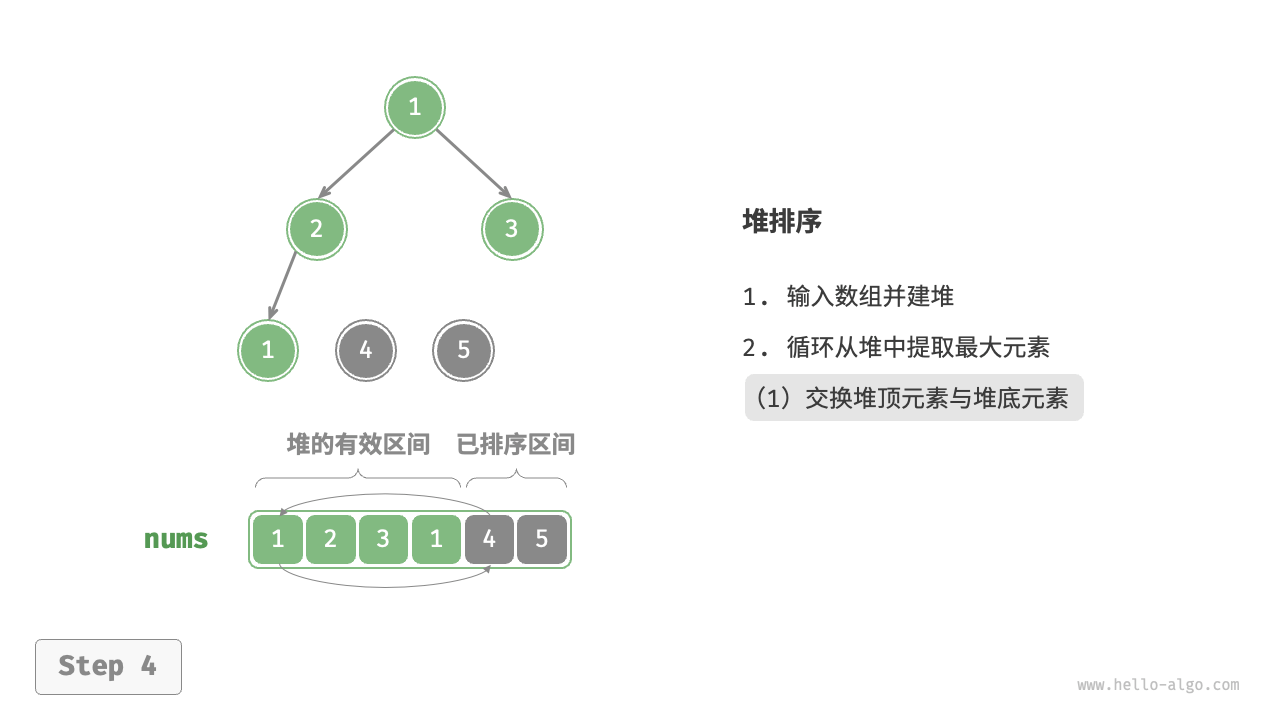
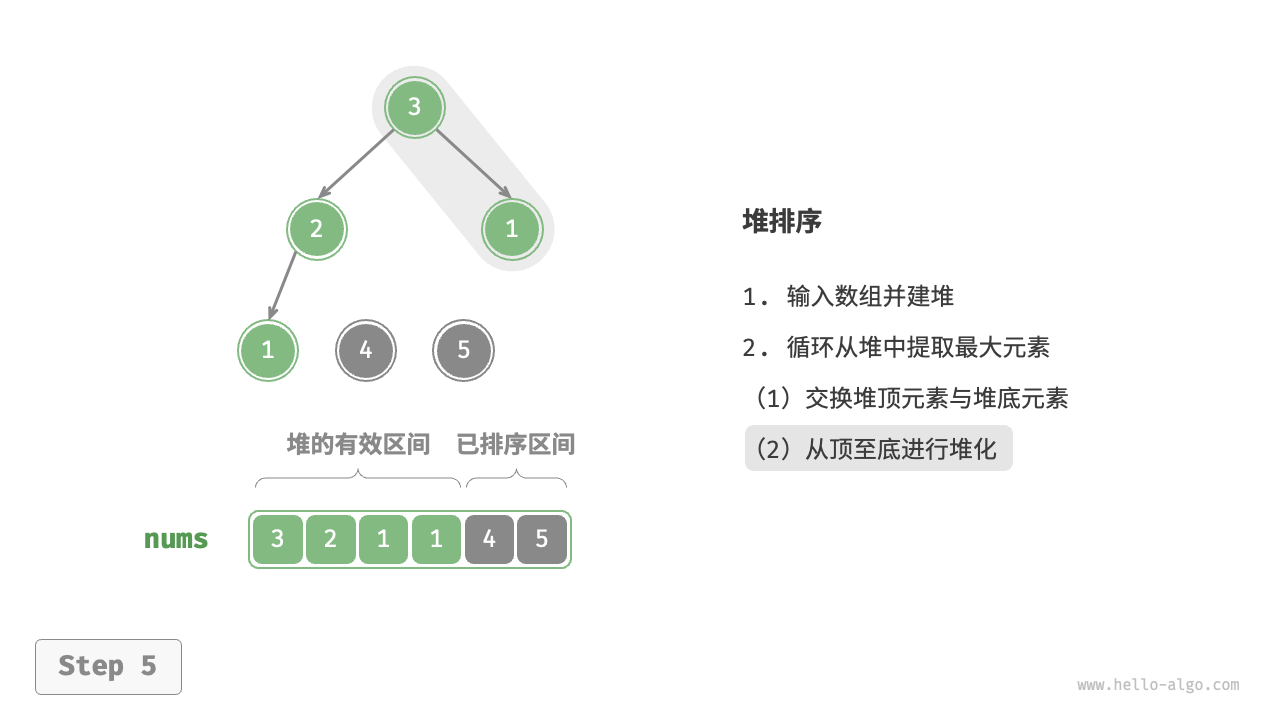
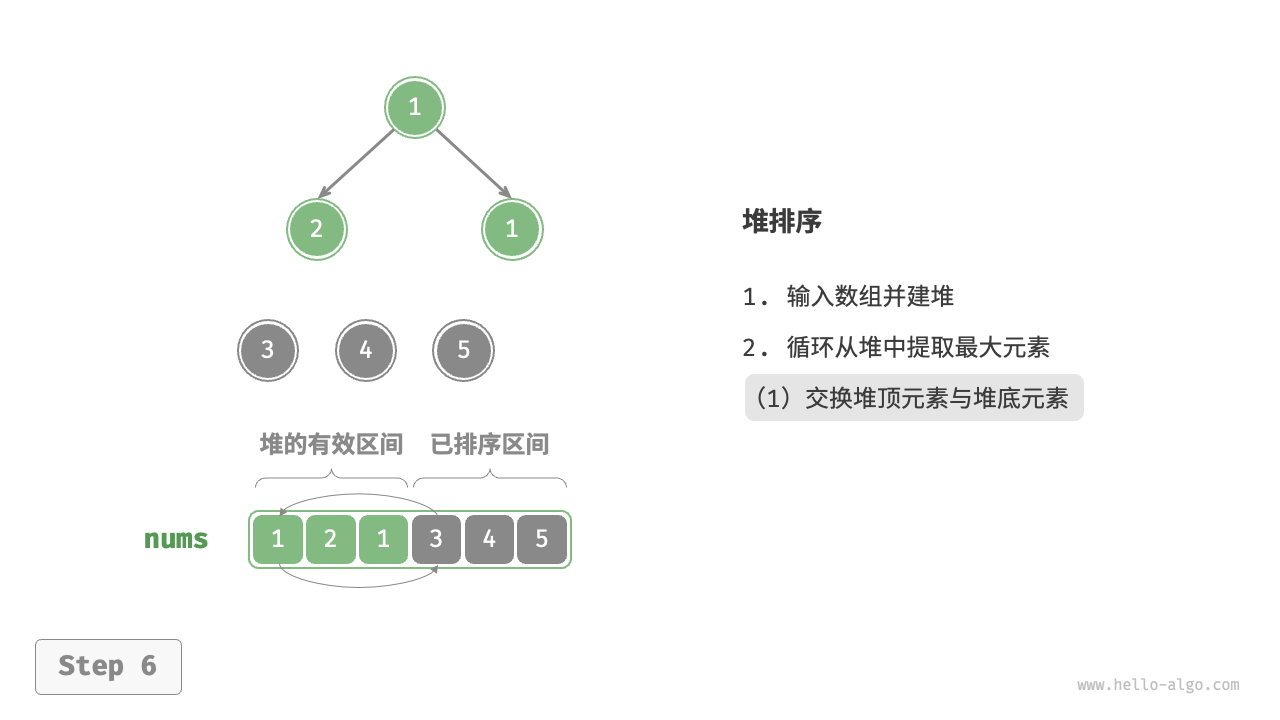
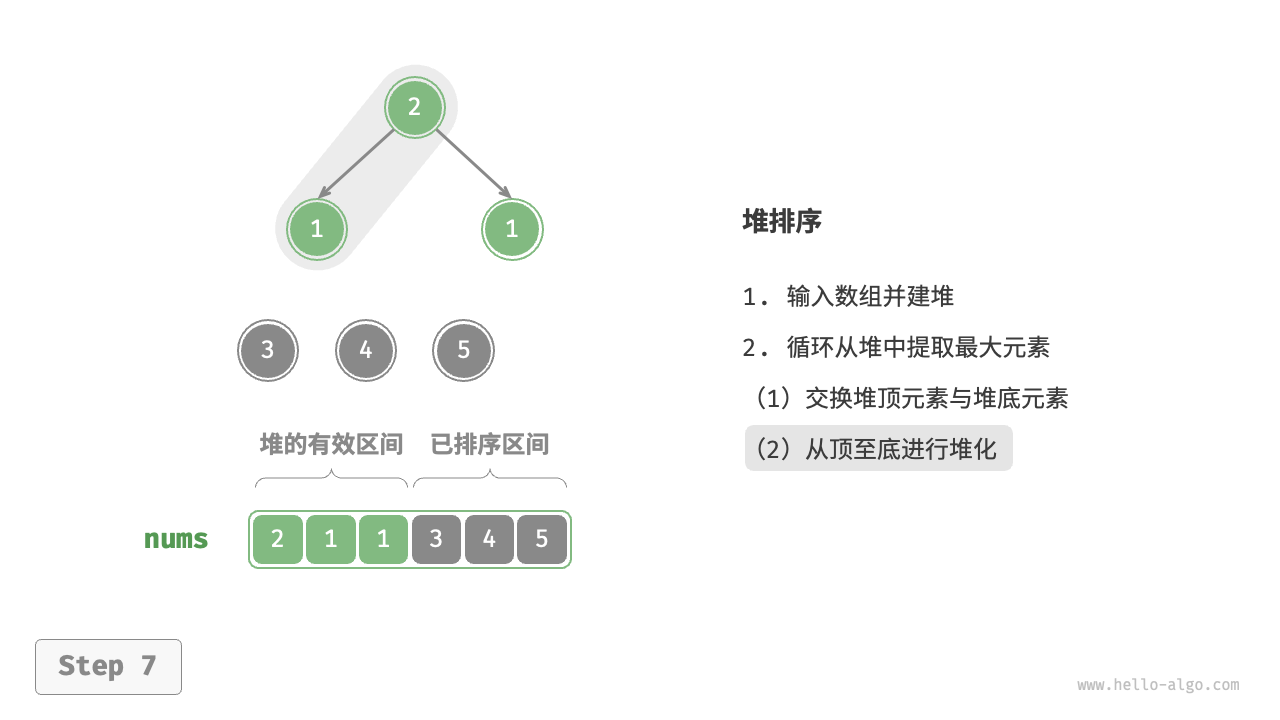
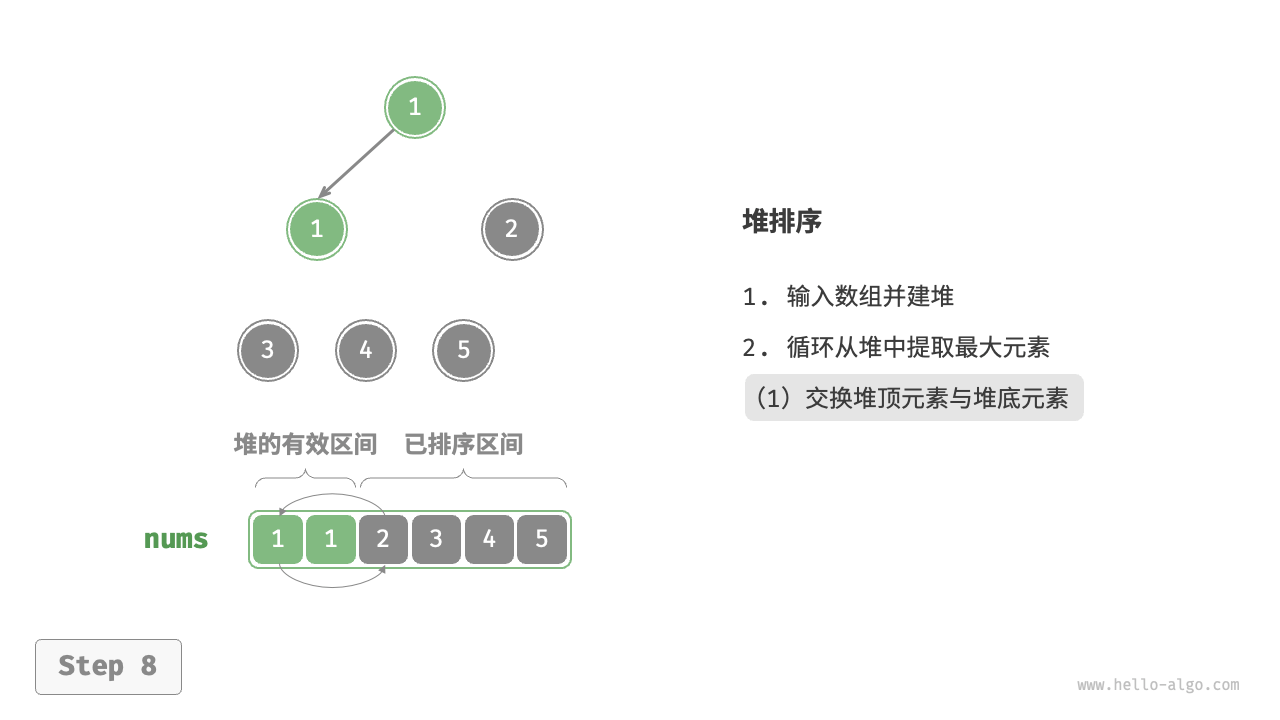
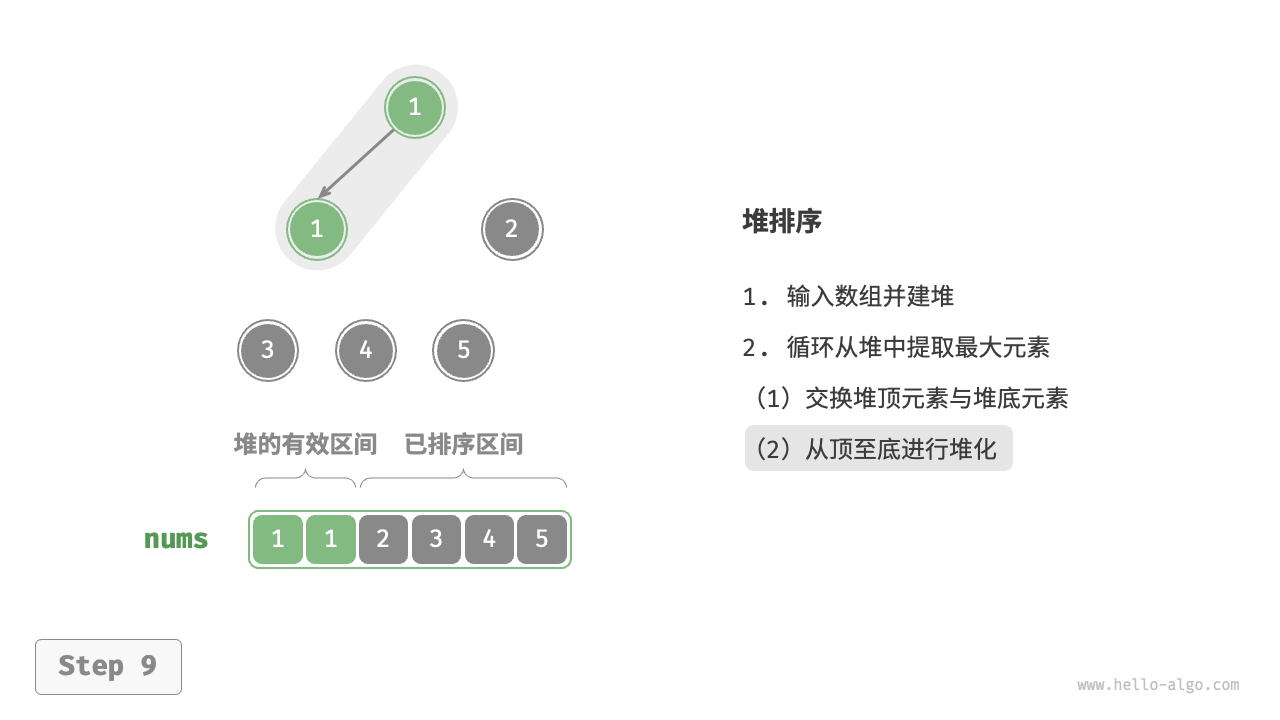
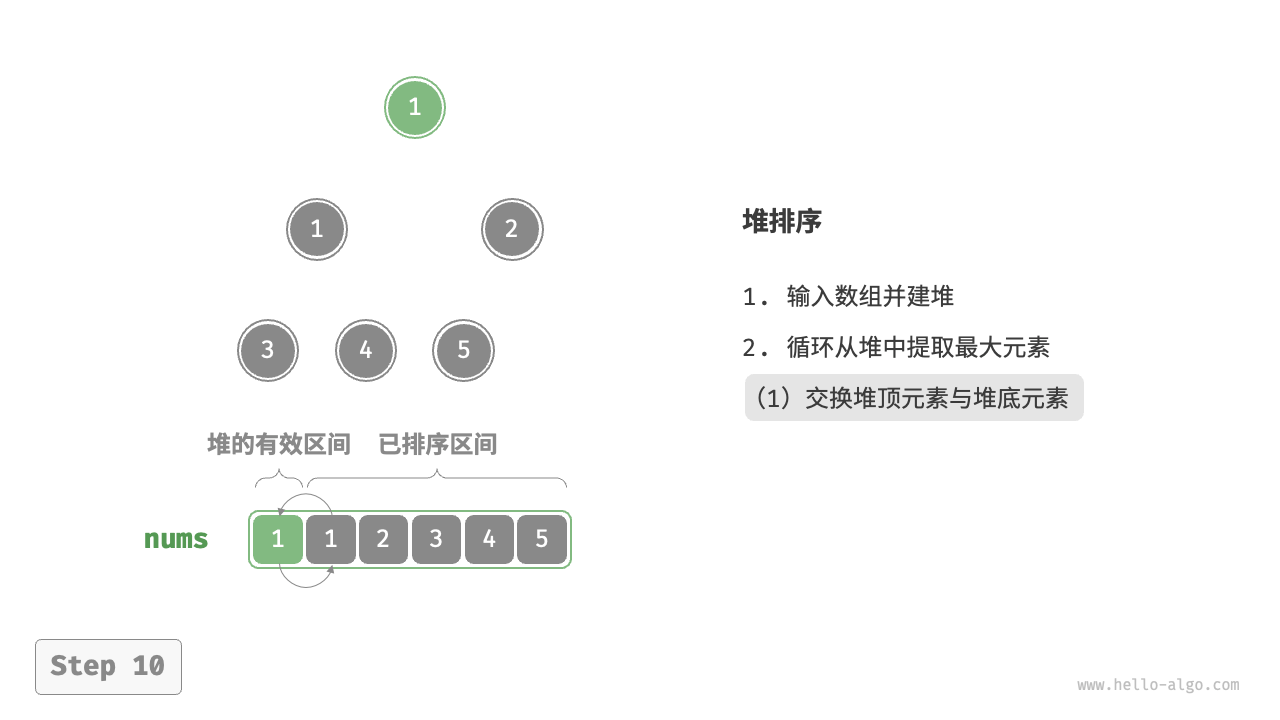
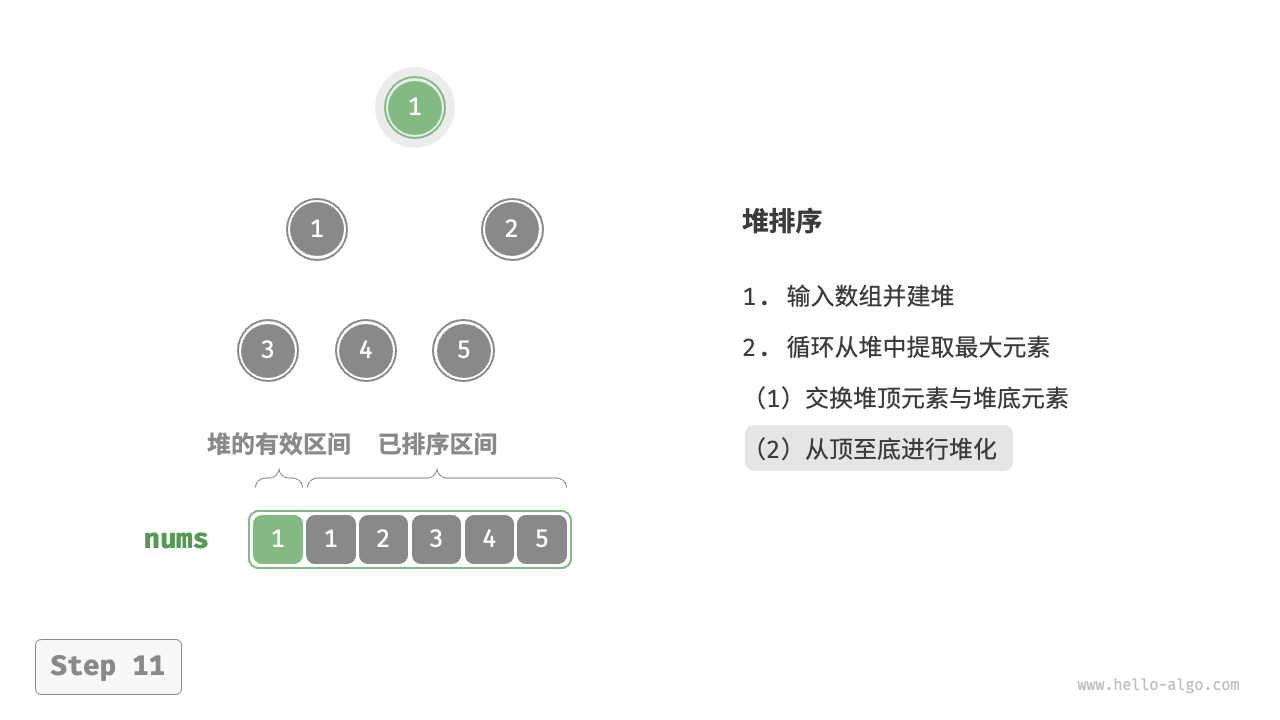
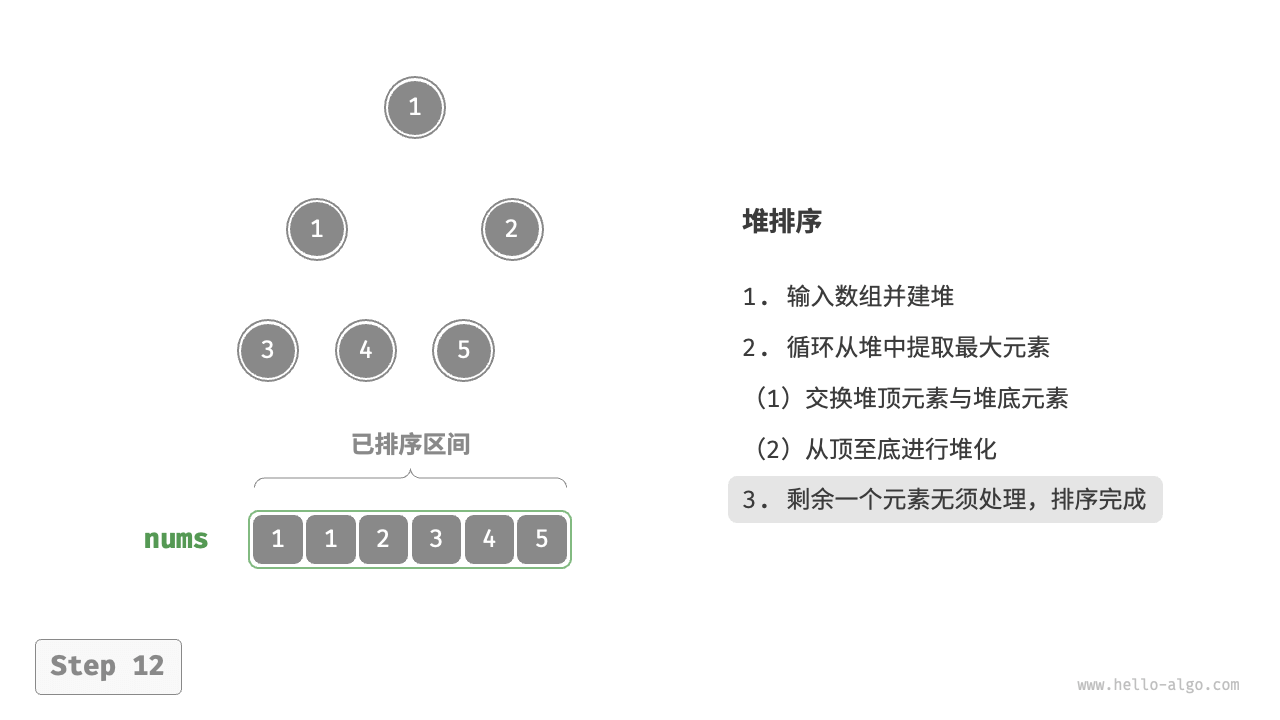
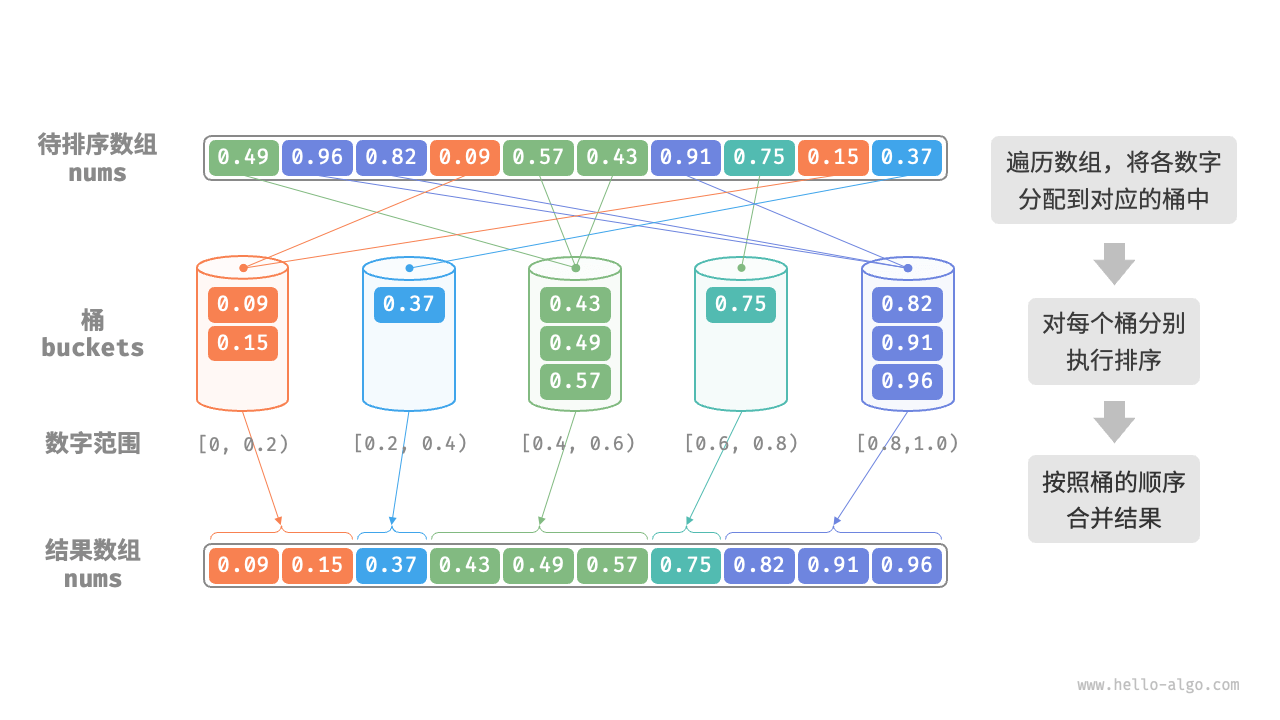
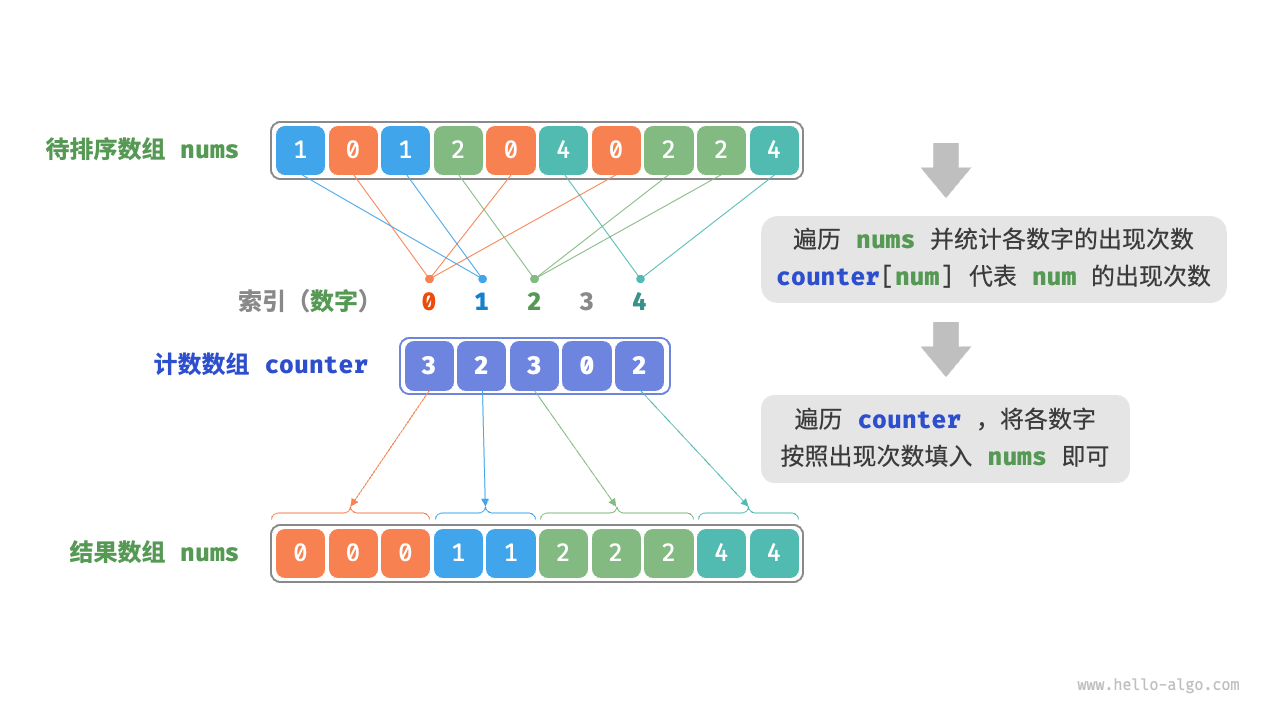
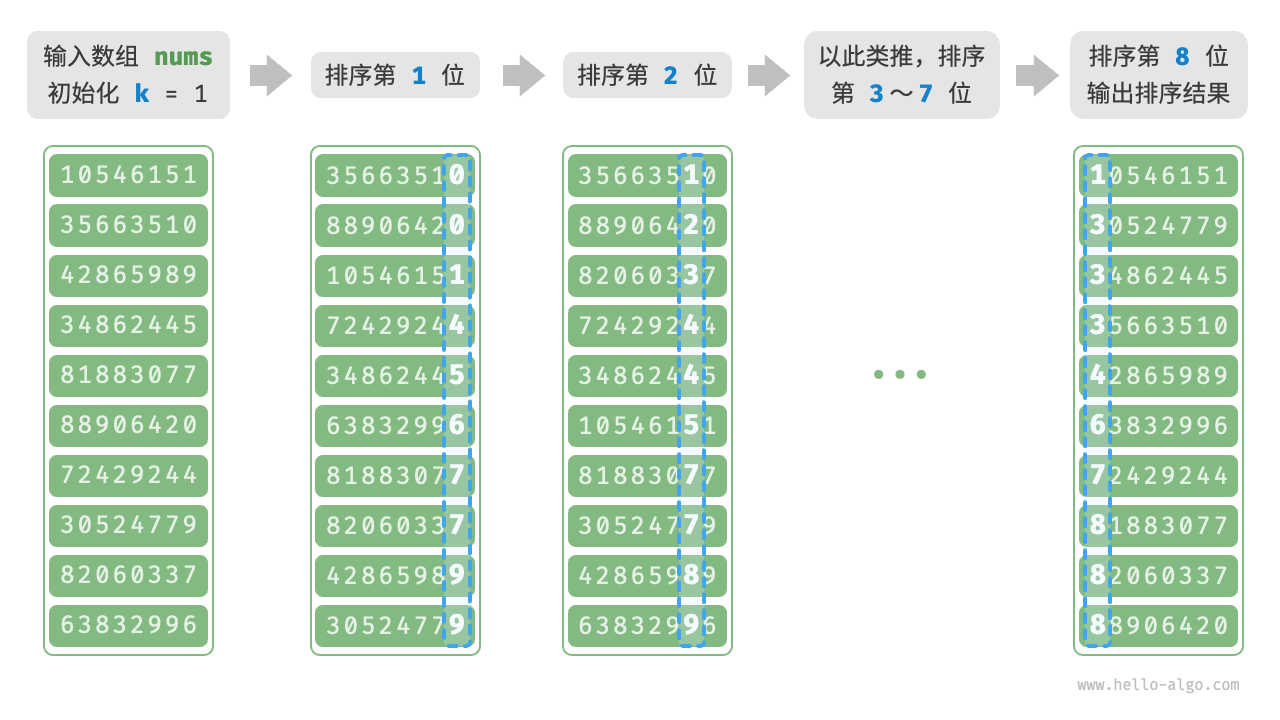
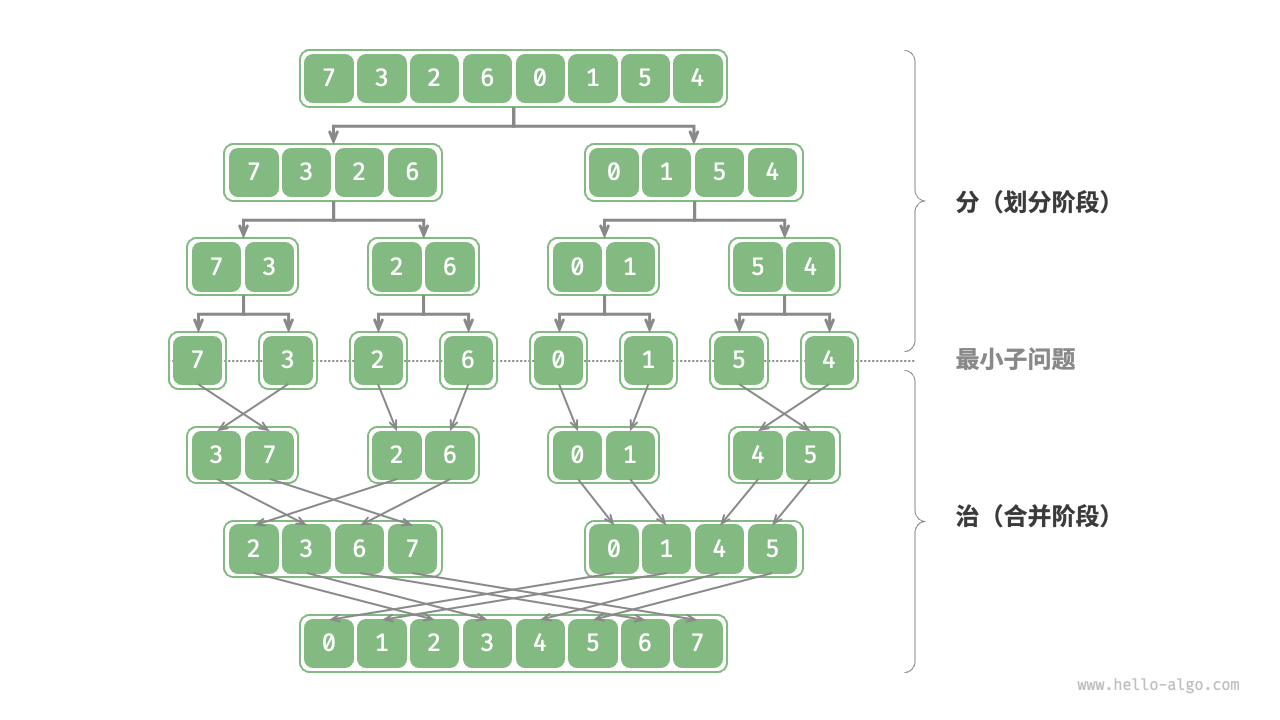

 浙公网安备 33010602011771号
浙公网安备 33010602011771号