软件工程作业(一)—最短路径问题
项目介绍
主要功能
提供一副地铁线路图(以北京地铁为例)
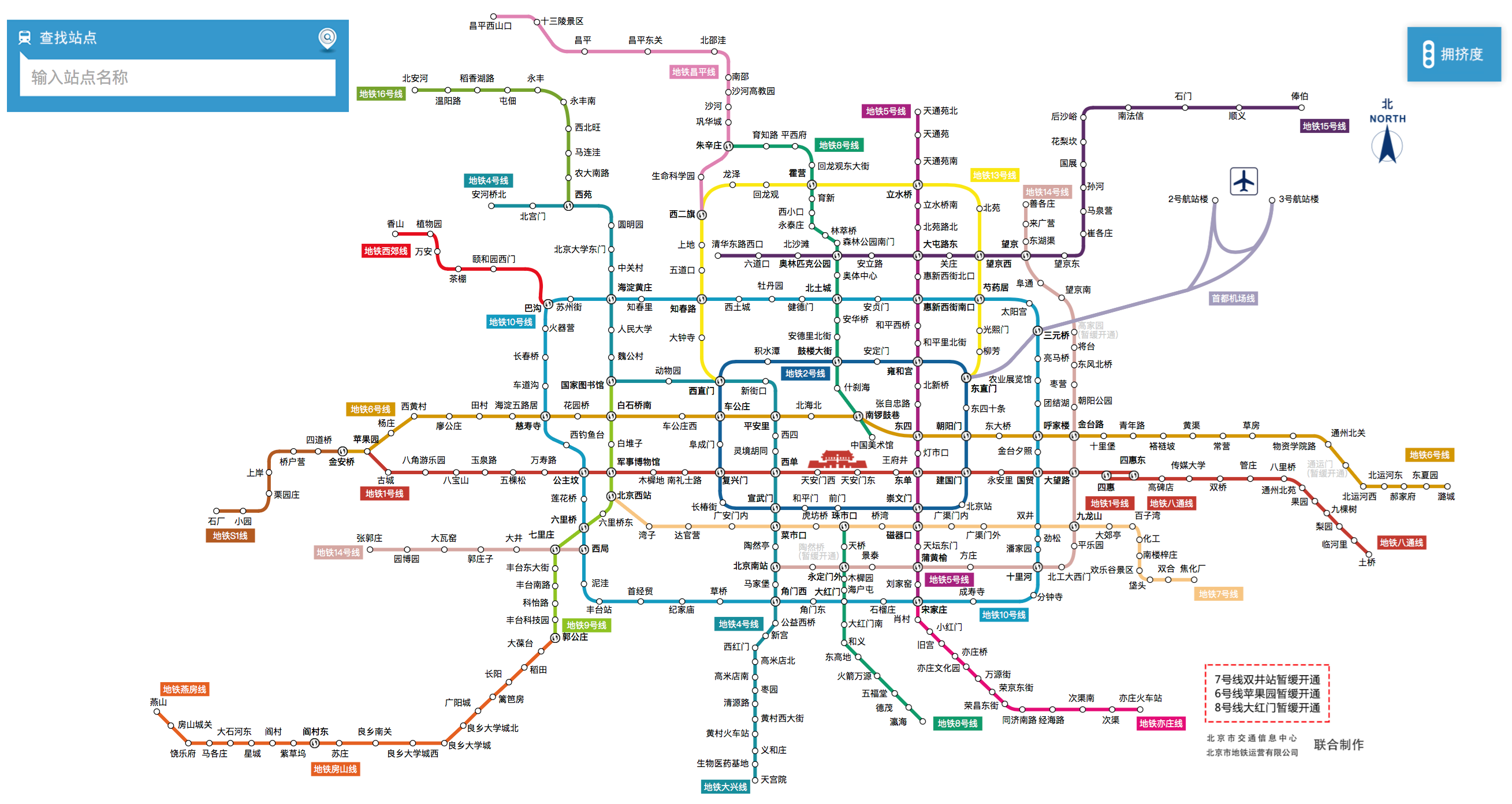
- 计算指定两站之间最短(最少经过站数)乘车路线;
- 输出指定地铁线路的所有站点。
- 写一篇个人博客,并将代码上传至github:https://github.com/nowaEve/Subway-Line-Shortest-Path
地铁线路信息保存在data.txt中,格式为
地铁线路总数
线路名1 站名1 站名2 站名3 ...
线路名2 站名1 站名2 站名3 ...
线路名3 站名1 站名2 站名3 ......
实现语言
Java
实现算法
Dijkstra算法
类职责划分
- LineModel:
private String name; //线名
private List<StationModel> stations; //该线中所有站的List
- StationModel:
private String StationName; //站名
private List<String> LineName; //该站所在线的线名的List
private List<StationModel> NeighborStation; //该站所临近的站的List
- ResultModel
//每一个站都有一个ResultModel,start为上一站,end为该站,distance为从起点到该站的距离,记录换乘
private StationModel start; //起点
private StationModel end; //途中到每个点最近的路,该点作为终点
private int distance = 0;
private boolean isExchange = false; //true为换乘,false为没有换乘
-
MainUtil
程序的入口,包含了核心代码,通过dijkstra找出最短路径。
-
DataProcessing
数据处理,将data.txt中的数据进行导入,并进行处理,建立图。
核心代码
DataProcessing
- 读入数据
File filename = new File(pathname);
InputStreamReader input = new InputStreamReader(new FileInputStream(filename));
BufferedReader br = new BufferedReader(input);
-
获取线的数量后,初始化即将被读入的线,循环读入该线中的站点;
-
每次读入站点,都要对当前站是否为换乘站和环线进行判断,如果是的话,该站的neighborStation就要进行添加,已经加入到线中的站点也要进行同步;
-
完善各个站点的neighborStation的添加;
-
将已经成型的Line加入到Line的集合LineSet中。
完整代码
public class DataProcessing {
public static List<LineModel> lineSet = new ArrayList<LineModel>(); //地铁线路信息
public DataProcessing(String pathname) throws IOException {
File filename = new File(pathname);
InputStreamReader input = new InputStreamReader(new FileInputStream(filename));
BufferedReader br = new BufferedReader(input);
String readstr = "";
readstr = br.readLine();
int numline = Integer.parseInt(readstr);
List<String> lines = new ArrayList<String>(); //所有的线名的集合
//获取线路图
for(int i=0;i<numline;i++) {
readstr = br.readLine();
String[] stationsOfLine = readstr.split(" ");
LineModel line = new LineModel();
List<StationModel> stations = new ArrayList<StationModel>();
line.setName(stationsOfLine[0]);//线路名
//处理每一个站点:换乘站,隔壁站.并加入到相应的线中
for(int j=0;j<stationsOfLine.length-1;j++) {
StationModel station = new StationModel();
List<String> lineName = new ArrayList<String>(); //每个站中的线名
List<StationModel> neighborStation = new ArrayList<StationModel>();
station.setStationName(stationsOfLine[j+1]);
int isExist = 0;
int isCircle = 0;
//确定是否为换乘站(已存在),lineSet不包括目前处理线
int flagnum=0,stationNum=0;
for(int lineindex = 0;lineindex<lineSet.size();lineindex++) {
for( int k=0;k<lineSet.get(lineindex).getStations().size();k++) {
if(stationsOfLine[j+1].equals(lineSet.get(lineindex).getStations().get(k).getStationName())) {
flagnum=lineindex;
stationNum = k;
station = lineSet.get(lineindex).getStations().get(k);
lineName = station.getLineName();
neighborStation = station.getNeighborStationName();
lineName.add(line.getName());
isExist = 1;
break;
}
}
}
if(isExist==0) { //该站还不存在
lineName.add(line.getName());
}
//添加neighborStation
//该line中已经存在该站了,为环线,且为最后一站,那么前面为换乘站已经判断过了
int p;
for(p=1;p<j+1;p++) {
if(stationsOfLine[p].equals(station.getStationName())) {
station = line.getOneStation(p-1);
lineName = station.getLineName();
neighborStation = station.getNeighborStationName();
}
}
//添加上一站到该站的neighbor列表
if(j!=0) {
neighborStation.add(line.getStations().get(j-1));
}
station.setLineName(lineName);
station.setNeighborStationName(neighborStation);
//等待station成型,添加这站到上一站的neighbor列表
if(j!=0) {
List<StationModel> newNeighborStations = new ArrayList<StationModel>();
newNeighborStations = line.getStations().get(j-1).getNeighborStationName();
newNeighborStations.add(station);
line.getStations().get(j-1).setNeighborStationName(newNeighborStations);
}
stations.add(station);
if(isExist == 1) {
List<StationModel> newStations = new ArrayList<StationModel>();
newStations = lineSet.get(flagnum).getStations();
newStations.set(stationNum, station);
lineSet.get(flagnum).setStations(newStations);
}
if(isCircle == 1) {
stations.set(p-1, station);
}
line.setStations(stations);
}
lineSet.add(line);
}
}
}
MainUtil
public static void searchLineData(String name)
根据线路名查找该线的所有站点
public static void searchLineData(String name) {
int flagnum=-1;
for(int i=0;i<dataProcessing.lineSet.size();i++) {
if(name.equals(dataProcessing.lineSet.get(i).getName())){
flagnum = i;
break;
}
}
if(flagnum==-1) {
System.out.print("该地铁线路不存在");
}
else {
System.out.print(name+": ");
for(StationModel stm:dataProcessing.lineSet.get(flagnum).getStations()) {
System.out.print(stm.getStationName()+" ");
}
}
}
public static void dijkstraToMin(String start,String end)
dijkstra算法查找两站之间的最佳路径(经过最短路径)
public static void dijkstraToMin(String start,String end) {
//作为neighbor刚被分析完的结果站点,等待进一步深度分析,分析它的neighbor,分析完了删除
List<StationModel> resultStation = new ArrayList<StationModel>();
//已经全部分析完的station,分析完一个就加入到这里,并将它的neighbor加入前一个List
List<StationModel> analyzedStation = new ArrayList<StationModel>();
//结果集
List<ResultModel> result = new ArrayList<ResultModel>();
//存放最终需要的站点的结果
List<ResultModel> endResult = new ArrayList<ResultModel>();
//找到起点
StationModel startStation = new StationModel();
startStation = findStation(start);
if(startStation==null) {
System.out.println("起点不存在");
System.exit(1);
}
//找到终点
StationModel endStation = new StationModel();
endStation = findStation(end);
if(endStation==null) {
System.out.println("终点不存在");
System.exit(1);
}
//起点终点结果相同
if(start.equals(end)) {
System.out.print("已经到达终点"+start);
System.exit(1);
}
//构建起点结果
ResultModel startResult = new ResultModel();
startResult.setDistance(0);
startResult.setStart(startStation);
startResult.setEnd(startStation);
startResult.setExchange(false);
ResultModel tempResult = new ResultModel();
StationModel tempStation = new StationModel();
result.add(startResult);
resultStation.add(startStation);
//通过neighbor的站点遍历,从待深度分析的station中get station
while(!resultStation.isEmpty()) {
tempStation = resultStation.get(0); //当前等待分析其neighbor的station
//tempResult中为以当前station为end的result,需要寻找从当前的结果集中
tempResult = findResult(tempStation, result);
//若在已经深度分析结束的List中,已经分析过邻居了
if(analyzedStation.contains(tempStation)) {
continue;
}
//若当前的tempResult已为最终需要的终点,已在结果集中,可以退出查找
if(tempStation.getStationName().equals(end)) {
break;
}
//遍历neighbor
for(int i=0;i<tempStation.getNeighborStationName().size();i++) {
int flag = 0;
ResultModel rm = new ResultModel(); //每一个station都只有一个result,其为result中end
StationModel stm = new StationModel(); //该station
stm = tempStation.getNeighborStationName().get(i);
//判断该station是否在结果集中,比较距离,更小的话就替换,如果进行了深度分析的话,说明当前待分析的距离一定>=该距离,已经为最小距离
for(int j=0;j<result.size();j++) {
if(result.get(j).getEnd().equals(stm)) {
flag = 1;
if(tempResult.getDistance()+1<result.get(j).getDistance()) {
//不可能发生
}
else {
break;
}
}
}
//在结果集中
if(flag==1) {
continue;
}
//不在结果集中,构建结果,并传入结果集,将station加入待深度分析
else {
rm.setDistance(tempResult.getDistance()+1);
rm.setStart(tempStation);
rm.setEnd(tempStation.getNeighborStationName().get(i));
result.add(rm);
resultStation.add(tempStation.getNeighborStationName().get(i));
}
}
analyzedStation.add(tempStation);
resultStation.remove(0);
}
endResult = findEndResult(start,end,result);
Collections.reverse(endResult);
if(endResult==null) {
System.out.println("终点不存在");
System.exit(1);
}
int number = endResult.size()+1;
System.out.println("共"+number+"站");
for(int i=0;i<endResult.size();i++) {
//换乘了,显示几号线
if(endResult.get(i).isExchange()) {
System.out.print(endResult.get(i).getEnd().getStationName());
System.out.println();
String str = new String();
str = returnExchangeLine(endResult.get(i).getStart(), endResult.get(i).getEnd(), endResult.get(i+1).getEnd());
System.out.println("->"+str);
}
if(i==0) {
String str = new String();
str = returnFirstLine(endResult.get(i).getEnd(), endResult.get(i).getStart());
System.out.println(str);
System.out.print(endResult.get(i).getStart().getStationName()+" ");
}
System.out.print(endResult.get(i).getEnd().getStationName()+" ");
}
}
在dijkstra函数用到的函数
在结果集中寻找需要的从起点到终点的结果
public static List<ResultModel> findEndResult(String start,String end,List<ResultModel> data) {
//根据终点开始遍历,直到找到起点,并且判断换乘,这站的前一站和后一站有没有同一条线
List<ResultModel> result = new ArrayList<ResultModel>();
String nowend = new String();
nowend = end;
int flag=0;
while(!nowend.equals(start)) {
for(int i=0;i<data.size();i++) {
if(data.get(i).getEnd().getStationName().equals(nowend)) {
result.add(data.get(i));
nowend = data.get(i).getStart().getStationName();
}
}
if(nowend.equals(start)) {
flag=1;
}
}
if(flag==1) {
//返回result前对是否换乘进行判断
for(int i=1;i<result.size();i++) {
if(i!=result.size()-1&&isExchange(result.get(i-1).getEnd(), result.get(i+1).getEnd())) {
result.get(i).setExchange(true);
}
}
return result;
}
else
return null;
}
其它函数
public static ResultModel findResult(StationModel s,List<ResultModel> result) {
for(ResultModel rm:result) {
if(rm.getEnd().getStationName().equals(s.getStationName())) {
return rm;
}
}
return null;
}
public static boolean isExchange(StationModel s1,StationModel s2) {
int isExchange = 1;
for(String ln1:s1.getLineName()) {
for(String ln2:s2.getLineName()) {
if(ln1.equals(ln2)) {
isExchange = 0;
//没有换乘
return false;
}
}
}
//换乘了
return true;
}
//寻找起点站
public static StationModel findStation(String name) {
StationModel station = new StationModel();
for(int i=0;i<dataProcessing.lineSet.size();i++) {
for(int j=0;j<dataProcessing.lineSet.get(i).getStations().size();j++) {
if(name.equals(dataProcessing.lineSet.get(i).getStations().get(j).getStationName())) {
station = dataProcessing.lineSet.get(i).getStations().get(j);
return station;
}
}
}
return null;
}
测试用例
-
查询路线,为环线

-
查询路线,不为环线
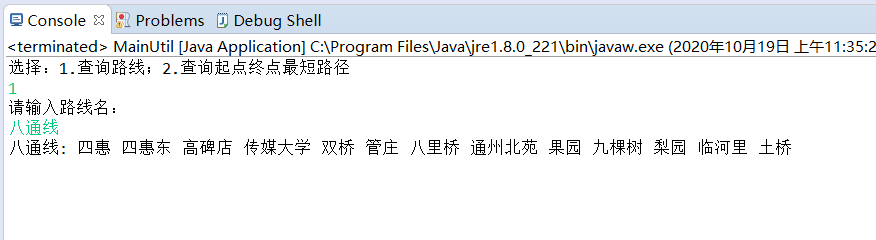
-
查询路线,路线不存在
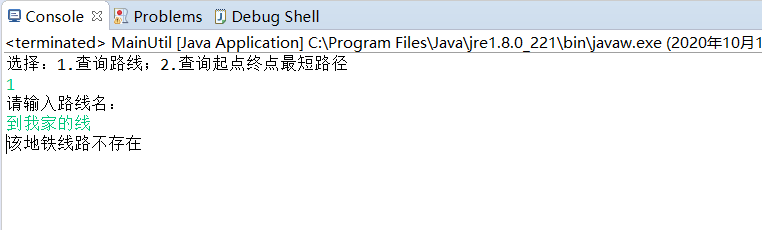
-
查询最佳路径,起点不存在

-
查询最佳路径,终点不存在
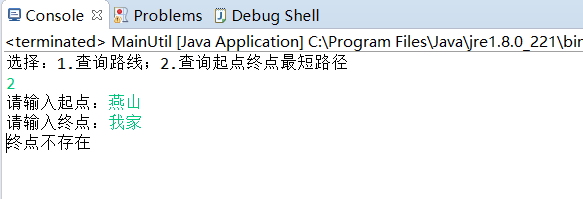
-
查询最佳路径,起点终点都在

-
查询最佳路径,起点终点相同
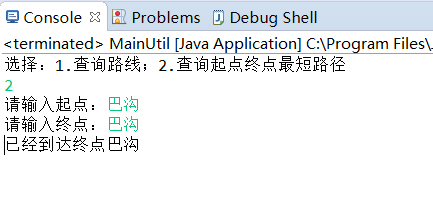
总结
从看题目到全部完成一共花了将近2天
整个过程分为
-
看题目,建立框架
-
数据传入并处理
-
dijkstra算法计算最佳路径
-
处理结果并输出
锻炼了我的代码能力和写博客的能力。
本题的全部代码已上传至github,地址为:https://github.com/nowaEve/Subway-Line-Shortest-Path



