[整理] 时间复杂度 (B-Tree树)

时间复杂度是一个函数，它定量描述了该算法的运行时间。

常见的时间复杂度有以下几种。
1，log(2)n，n，n log(2)n ，n的平方，n的三次方，2的n次方，n!

1指的是常数。即，无论算法的输入n是多大，都不会影响到算法的运行时间。这种是最优的算法。而n！（阶乘）是非常差的算法。当n变大时，算法所需的时间是不可接受的。

用通俗的话来描述，我们假设n=1所需的时间为1秒。那么当n = 10，000时。

• O（1）的算法需要1秒执行完毕。
• O（n）的算法需要10，000秒 ≈ 2.7小时 执行完毕。
• O（n2）的算法需要100，000，000秒 ≈ 3.17年 执行完毕。
• O（n！）的算法需要XXXXXXXX(系统的计算器已经算不出来了)。
  可见算法的时间复杂度影响有多大。

---

假如一张表有一亿条数据 ，需要查找其中某一条数据，按照常规逻辑，一条一条的去匹配的话，最坏的情况下需要匹配一亿次才能得到结果，用大O标记法就是O(n)最坏时间复杂度。
这是无法接受的，而且这一亿条数据显然不能一次性读入内存供程序使用， 因此，这一亿次匹配在不经缓存优化的情况下就是一亿次IO开销，以现在磁盘的IO能力和CPU的运算能力，有可能需要几个月才能得出结果 。

如果把这张表转换成平衡树结构（一棵非常茂盛和节点非常多的树），

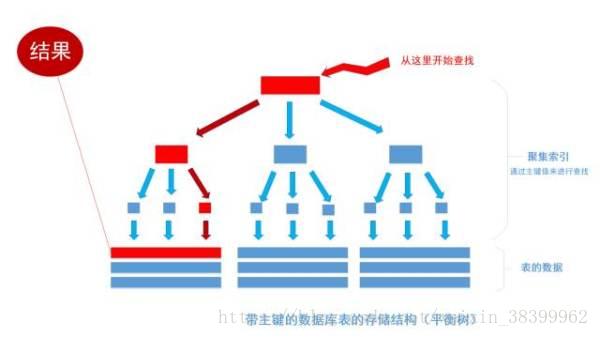
(图示:该树只有三个节点)

假设这棵树有10层，那么只需要10次IO开销就能查找到所需要的数据， 速度以指数级别提升，用大O标记法就是O(log n)，n是记录总树，底数是树的分叉数，结果就是树的层次数。换言之，查找次数是以树的分叉数为底，记录总数的对数，用公式来表示就是

\[\log_{树的分叉数}{记录总数} = 查找次数 \]

用程序来表示就是Math.Log(100000000,10)，100000000是记录数，10是树的分叉数（真实环境下分叉数远不止10）， 结果就是查找次数，这里的结果从亿降到了个位数。因此，利用索引会使数据库查询有惊人的性能提升。