[整理] JDK8中Arrays.sort的排序算法

点进sort方法：

// Use Quicksort on small arrays
if (right - left < QUICKSORT_THRESHOLD) {//QUICKSORT_THRESHOLD = 286
  sort(a, left, right, true);
  return;
}

点进去sort(a, left, right, true);方法：

// Use insertion sort on tiny arrays
    if (length < INSERTION_SORT_THRESHOLD) { //INSERTION_SORT_THRESHOLD（47）
        if (leftmost) {
        ......

 如果元素少于47这个阀值，就用插入排序

            /*
             * Traditional (without sentinel) insertion sort,
             * optimized for server VM, is used in case of
             * the leftmost part.
             */
            for (int i = left, j = i; i < right; j = ++i) {
                int ai = a[i + 1];
                while (ai < a[j]) {
                    a[j + 1] = a[j];
                    if (j-- == left) {
                        break;
                    }
                }
                a[j + 1] = ai;

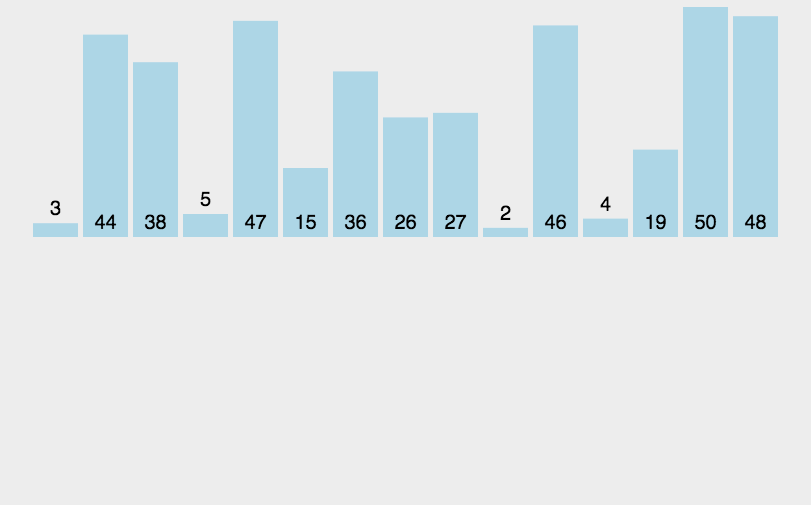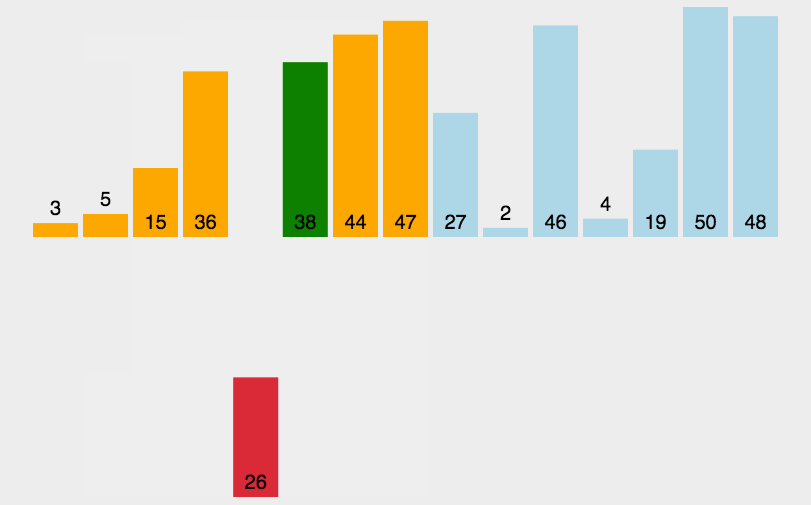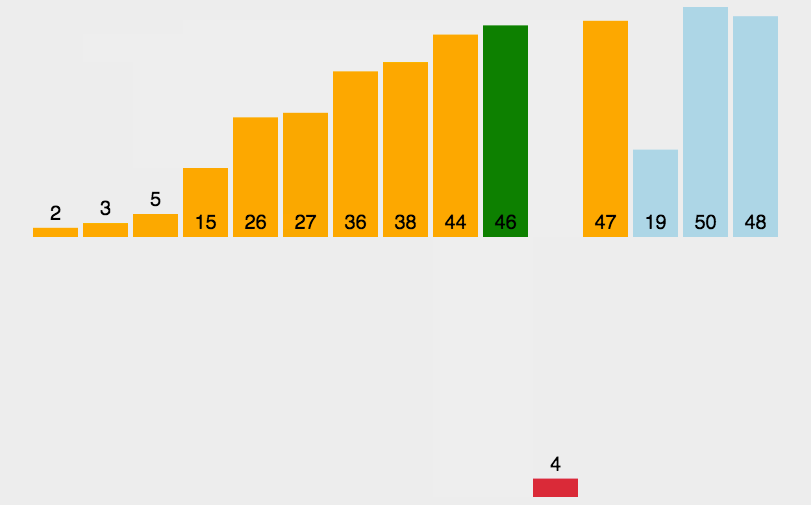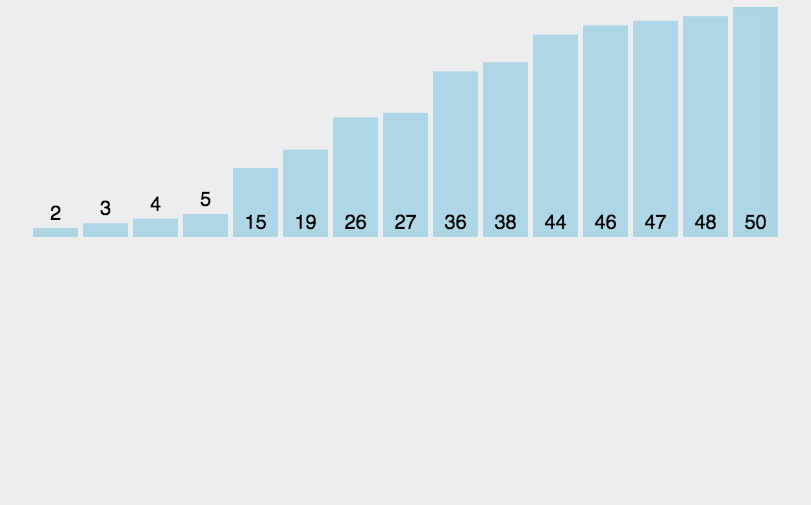
 插入排序

 

大过INSERTION_SORT_THRESHOLD（47）的，用一种快速排序的方法：
1.从数列中挑出五个元素，称为 “基准”（pivot）；
2.重新排序数列，所有元素比基准值小的摆放在基准前面，所有元素比基准值大的摆在基准的后面（相同的数可以到任一边）。在这个分区退出之后，该基准就处于数列的中间位置。这个称为分区（partition）操作；
3.递归地（recursive）把小于基准值元素的子数列和大于基准值元素的子数列排序。

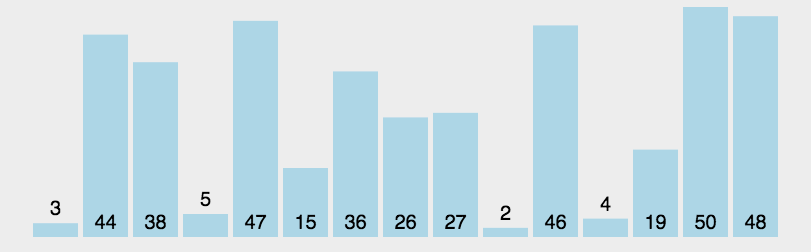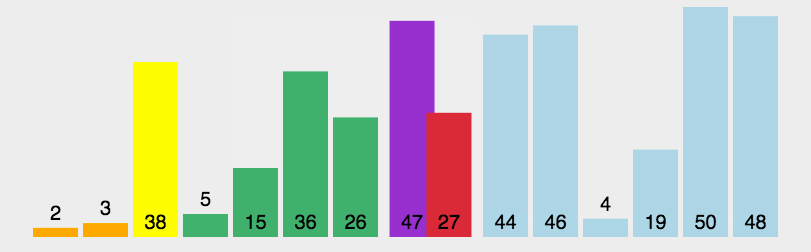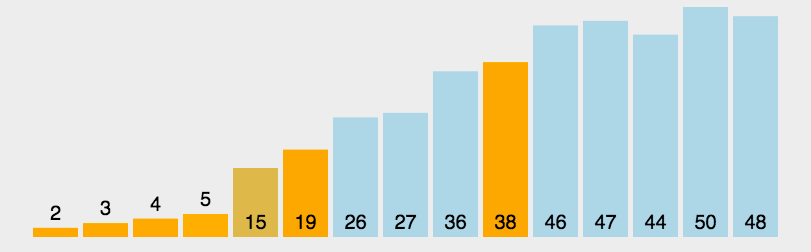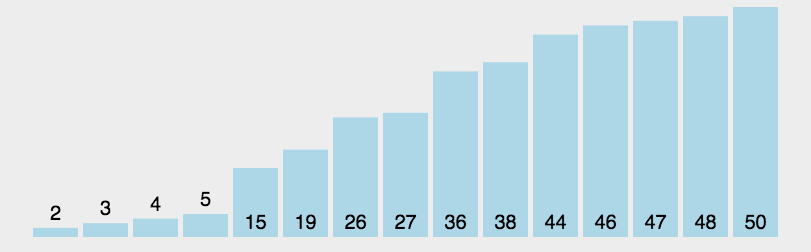
快速排序（Quick Sort）

 

至于大于286的，它会进入归并排序（Merge Sort），但在此之前，它有个小动作：

    // Check if the array is nearly sorted
    for (int k = left; k < right; run[count] = k) {
        if (a[k] < a[k + 1]) { // ascending
            while (++k <= right && a[k - 1] <= a[k]);
        } else if (a[k] > a[k + 1]) { // descending
            while (++k <= right && a[k - 1] >= a[k]);
            for (int lo = run[count] - 1, hi = k; ++lo < --hi; ) {
                int t = a[lo]; a[lo] = a[hi]; a[hi] = t;
            }
        } else { // equal
            for (int m = MAX_RUN_LENGTH; ++k <= right && a[k - 1] == a[k]; ) {
                if (--m == 0) {
                    sort(a, left, right, true);
                    return;
                }
            }
        }

        /*
         * The array is not highly structured,
         * use Quicksort instead of merge sort.
         */
        if (++count == MAX_RUN_COUNT) {
            sort(a, left, right, true);
            return;
        }
    }

这里主要作用是看他数组具不具备结构：实际逻辑是分组排序，每降序为一个组，像1,9,8,7,6,8。9到6是降序，为一个组，然后把降序的一组排成升序：1,6,7,8,9,8。然后最后的8后面继续往后面找。。。

每遇到这样一个降序组，++count，当count大于MAX_RUN_COUNT（67），被判断为这个数组不具备结构（也就是这数据时而升时而降），然后送给之前的sort(里面的快速排序)的方法（The array is not highly structured,use Quicksort instead of merge sort.）。

如果count少于MAX_RUN_COUNT（67）的，说明这个数组还有点结构，就继续往下走下面的归并排序：

   // Determine alternation base for merge
    byte odd = 0;
    for (int n = 1; (n <<= 1) < count; odd ^= 1);

从这里开始，正式进入归并排序（Merge Sort）！

    // Merging
    for (int last; count > 1; count = last) {
        for (int k = (last = 0) + 2; k <= count; k += 2) {
            int hi = run[k], mi = run[k - 1];
            for (int i = run[k - 2], p = i, q = mi; i < hi; ++i) {
                if (q >= hi || p < mi && a[p + ao] <= a[q + ao]) {
                    b[i + bo] = a[p++ + ao];
                } else {
                    b[i + bo] = a[q++ + ao];
                }
            }
            run[++last] = hi;
        }
        if ((count & 1) != 0) {
            for (int i = right, lo = run[count - 1]; --i >= lo;
                b[i + bo] = a[i + ao]
            );
            run[++last] = right;
        }
        int[] t = a; a = b; b = t;
        int o = ao; ao = bo; bo = o;
    }

总结：
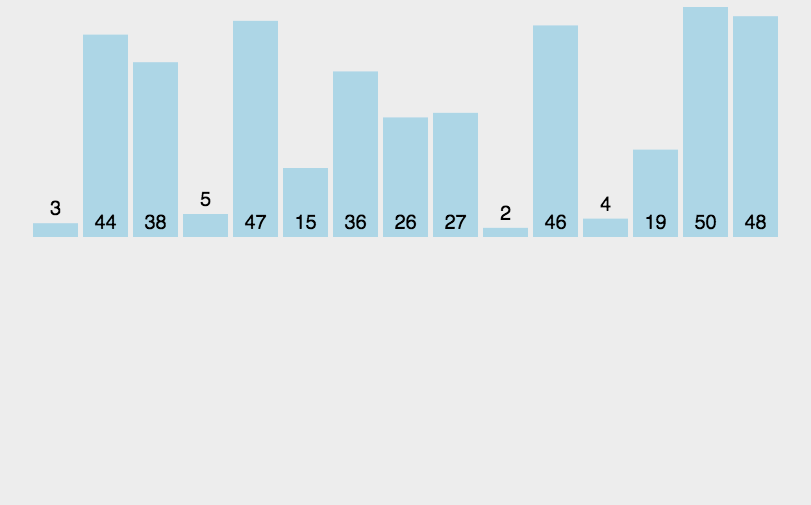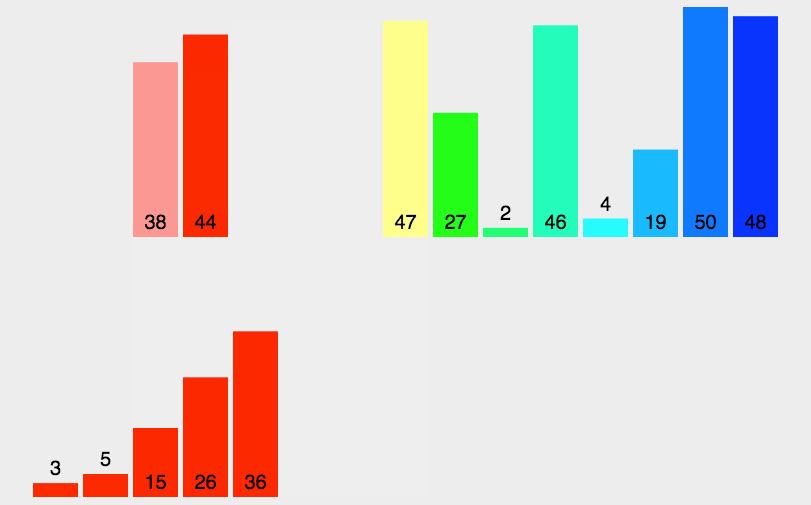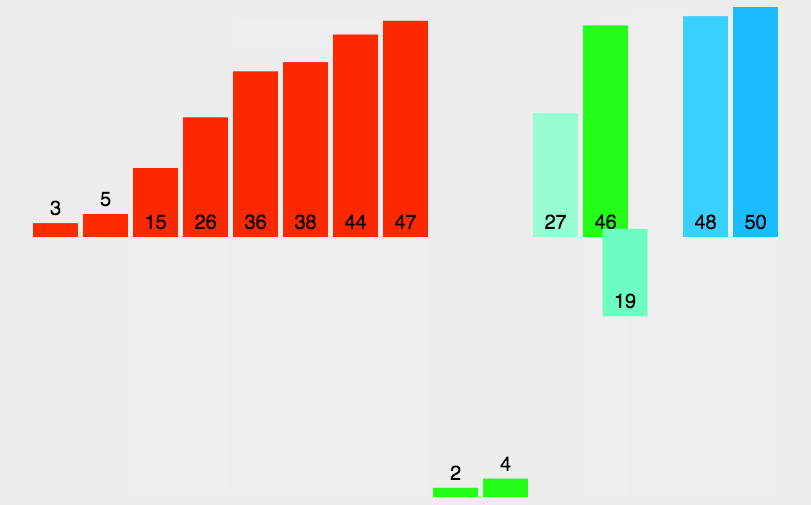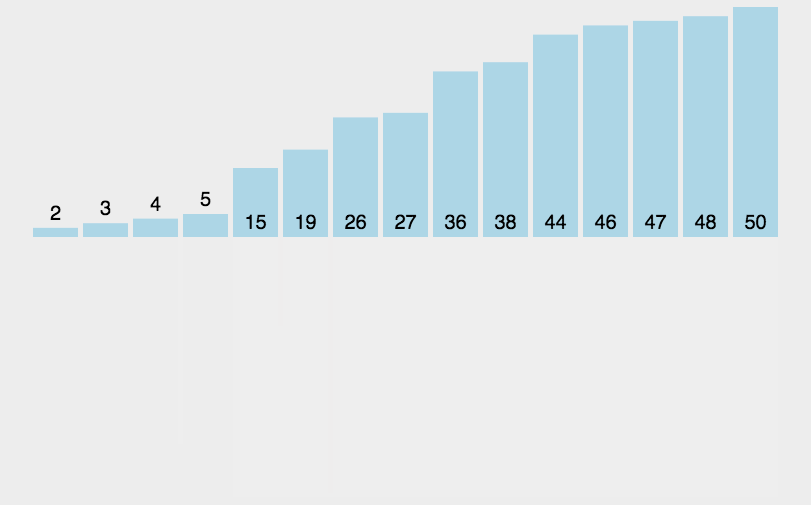
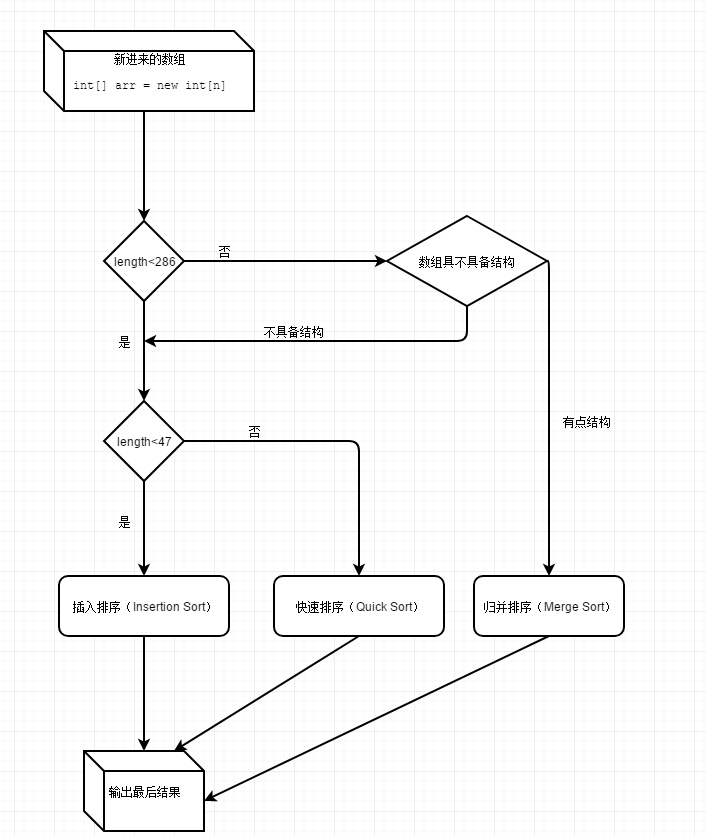
从上面分析，Arrays.sort并不是单一的排序，而是插入排序，快速排序，归并排序三种排序的组合，流程图如下：