图概念总结

一.思维导图

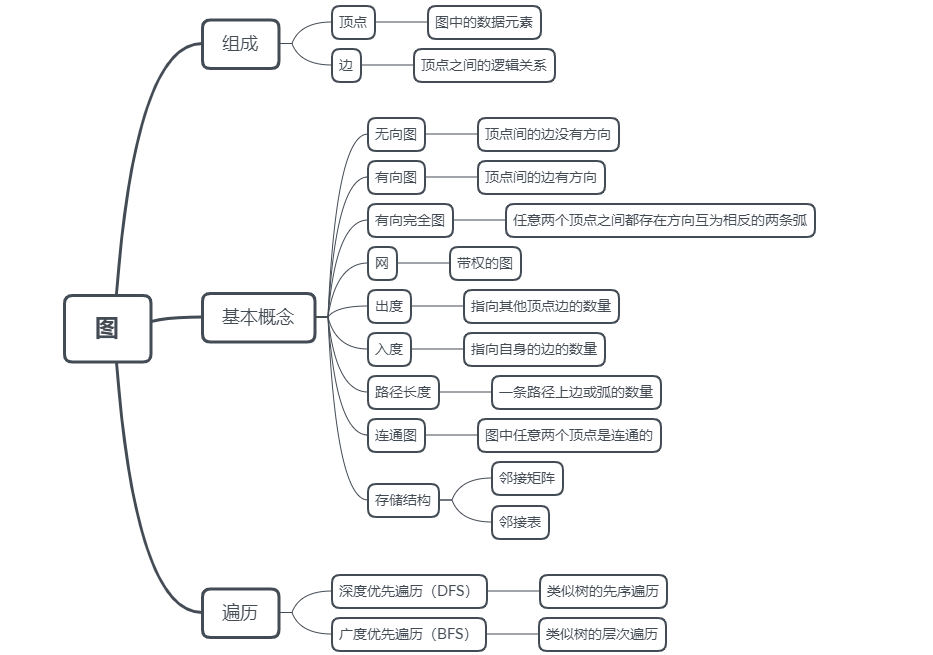
二.重要的概念

深度优先遍历

深度优先遍历在遍历过程中每当访问到某一个顶点后，需要递归地访问此顶点的所有未访问过的相邻顶点。因而，这种遍历将尽可能深地持续探索，直到无法继续为止。

广度优先遍历

广度优先遍历在探索图中的顶点之前，先访问当前顶点的所有邻接顶点。

最小生成树

1.普利姆算法（prime）

先选中一个结点，在剩下所有结点与该结点的所有边中选一条最短的边，将这条边的顶点选出，然后重复之前的操作，直到所有结点遍历完，这时就能得到最小生成树。

时间复杂度 ：O(n^2)

适用于稠密网

2.克鲁斯卡尔算法（ kluskal）

将所有边按照权值的大小进行升序排序，然后从小到大一一判断 ，且要保证每次选择的边和之前的边集不能构成回路。

时间复杂度：O(eloge)

适用于稀疏网

最短路径

1.迪杰斯特拉算法（Dijkstra)

把图中的顶点集合V分成两组，第一组为已求出最短路径的顶点集合S；第二组是未确定最短路径的顶点集合U。

1. 初始化时，S中只有初始结点
2. 从U中选取一个距离v最小的顶点k加入S中
3. 以k为中间点，修改U中各顶点的距离；若从初始结点v到顶点u的距离（经过顶点k）比原来距离（不经过顶点k）短，则修改顶点u的距离值，修改后的距离值是顶点k的距离加上k到u的距离
4. 重复步骤第2步和第3步，直到终点进入S

2.弗洛伊德算法（Floyd）

1. 从任意一条单边路径开始。所有两点之间的距离是边的权，如果两点之间没有边相连，则权为∞
2. 对于每一对顶点 u 和 v，看看是否存在一个顶点 w 使得从 u 到 w 再到 v 比已知的路径更短。如果是则更新它
3. 重复直到更新到终点

三.疑难问题