强化学习学习笔记（5）：

在前面的介绍中，我们都是使用参数θ近似动作值或状态值函数，

\(\begin{array}{l} {V_\theta }\left( s \right) \approx {V^\pi }\left( s \right) \\ {Q_\theta }\left( {s,a} \right) \approx {Q^\pi }\left( {s,a} \right) \\ \end{array}\)
直接从价值函数生成策略，比如使用贪婪策略，也就是选择值函数最大的方法来确定最优策略。
在本节中，我们将直接对策略进行参数化
\({\pi _\theta }\left( {s,a} \right) = {\rm P}\left[ {a\left| {s,\theta } \right.} \right]\)
我们将再次专注于无模型的强化学习

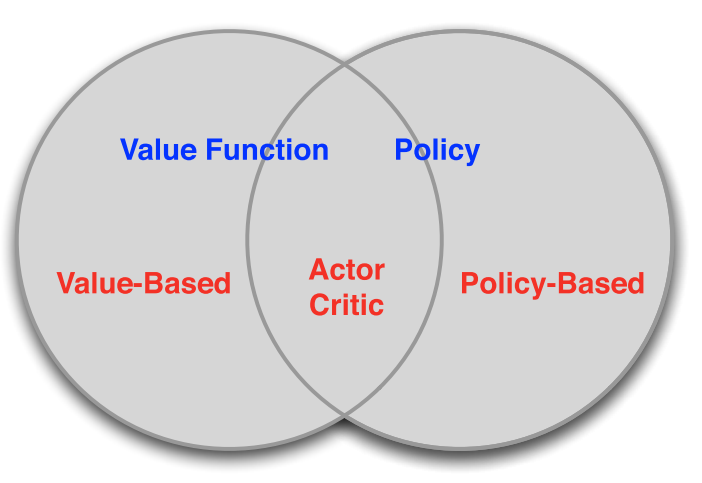
基于值
学习价值函数
隐性策略
基于策略
没有值函数
直接学习策略
Actor-Critic
学习值函数，学习策略。
直接策略强化学习方法有以下优点
更好的收敛性
在高维或连续动作空间中有效
可以学习随机策略
但也有一些缺点
通常收敛到局部而不是全局最优
评估策略通常效率低下且方差很大

目标：给的策略\({\pi _\theta }\left( {s,a} \right)\)，寻找最优的参数 \(\[\theta \]\)
在情景环境中，我们可以使用初始值
\({J_1}\left( \theta \right) = {V^{{\pi _\theta }}}\left( {{s_1}} \right) = {{\rm E}_{{\pi _\theta }}}\left[ {{v_1}} \right]\)
在持续的环境中，我们可以使用平均值
\({J_{av}}{}_V\left( \theta \right) = {\sum\limits_s {{d^{{\pi _\theta }}}\left( s \right)V} ^{{\pi _\theta }}}\left( s \right)\)
或每个时间步的平均奖励
${J_{av}}{}_R\left( \theta \right) = \sum\limits_s {{d^{{\pi _\theta }}}\left( s \right)\sum\limits_a {{\pi _\theta }\left( {s,a} \right)} R_s^a} \( 基于策略的强化学习是一个优化问题，寻找是\)J\left( \theta \right)$ 最大的参数$\theta \( 使用梯度通常可以提高效率，包括梯度下降，共轭梯度，准牛顿。我们专注于梯度下降，可能有许多扩展。以及利用顺序结构的方法。 通过提高政策的梯度，策略梯度方法搜索\)J\left( \theta \right)\(的一个局部最大值。 \)\Delta \theta = \alpha {\nabla _\theta }J\left( \theta \right)\( 其中，\){\nabla _\theta }J\left( \theta \right)\(是策略梯度。 \){\nabla _\theta }J\left( \theta \right) = \left( {\begin{array}{*{20}{c}}
{\frac{{\partial J\left( \theta \right)}}{{\partial {\theta _1}}}} \
\vdots \
{\frac{{\partial J\left( \theta \right)}}{{\partial {\theta _n}}}} \
\end{array}} \right)\( α是步长参数 为了评估\){\pi _\theta }\left( {s,a} \right)\(的策略梯度，对于每一个维度\)k \in \left[ {1,n} \right]\( 估计目标函数的第k个偏导数w.r.t. θ，通过第k维的小扰动\)\varepsilon \( \)\frac{{\partial J\left( \theta \right)}}{{\partial {\theta _k}}} \approx \frac{{J\left( {\theta + \varepsilon {u_k}} \right) - J\left( \theta \right)}}{\varepsilon }\( 使用n个评估来计算n个维度中的策略梯度，简单，嘈杂，效率低下-但有时有效。适用于任意策略，即使策略不可区分。 现在，我们分析计算策略梯度，假设策略πθ非零时是可微的，并且我们知道梯度\){\nabla _\theta }{\pi _\theta }\left( {s,a} \right)$
可能性比利用以下

\(\begin{array}{l} {\nabla _\theta }{\pi _\theta }\left( {s,a} \right) = {\pi _\theta }\left( {s,a} \right)\frac{{{\nabla _\theta }{\pi _\theta }\left( {s,a} \right)}}{{{\pi _\theta }\left( {s,a} \right)}} \\ = {\pi _\theta }\left( {s,a} \right){\nabla _\theta }\log {\pi _\theta }\left( {s,a} \right) \\ \end{array}\)
得分函数是\(\log {\pi _\theta }\left( {s,a} \right)\)
我们将使用softmax策略作为运行示例,使用特征$\phi {\left( {s,a} \right)^{\rm T}}\theta \(的线性组合进行权重动作，动作概率与加权指数成正比 \){\pi _\theta }\left( {s,a} \right) \propto {e^{\phi {{\left( {s,a} \right)}^{\rm T}}\theta }}\( 得分函数为： \){\nabla _\theta }\log {\pi \theta }\left( {s,a} \right) = \phi \left( {s,a} \right) - {{\rm E}{{\pi _\theta }}}\left[ {\phi \left( {s, \cdot } \right)} \right]$

在连续动作空间中，自然会采用高斯策略,均值是状态特征的线性组合$u\left( s \right) = \phi {\left( s \right)^{\rm T}}\theta \(。 方差是\){{\sigma ^2}}\( 策略是高斯分布，\)a \sim N\left( {\mu \left( s \right),{\sigma ^2}} \right)\( 得分函数为： \){\nabla \theta }\log {\pi \theta }\left( {s,a} \right) = \frac{{\left( {a - \mu \left( s \right)} \right)\phi \left( s \right)}}{{{\sigma ^2}}}\( 考虑一类简单的一步式MDP,使用似然比来计算策略梯度 \)\begin{array}{l}
J\left( \theta \right) = {{\rm E}{{\pi \theta }}}\left[ r \right] \
= \sum\limits {d\left( s \right)} \sum\limits {{\pi \theta }\left( {s,a} \right){R{s,a}}} \
{\nabla \theta }J\left( \theta \right) = \sum\limits {d\left( s \right)} \sum\limits_{a \in A} {{\pi _\theta }\left( {s,a} \right){\nabla _\theta }\log {\pi \theta }\left( {s,a} \right)} \
= {{\rm E}{{\pi _\theta }}}\left[ {{\nabla _\theta }\log {\pi _\theta }\left( {s,a} \right)r} \right] \
\end{array}\( 策略梯度定理推广了多步MDP的似然比方法,用长期值\){Q^\pi }\left( {s,a} \right)$代替瞬时奖励r,策略梯度定理适用于初始状态目标，平均奖励和平均值目标

Monte-Carlo Policy Gradient,通过随机梯度上升来更新参数,使用策略梯度定理
将return vt用作Qπθ的无偏样本,
\(\Delta {\theta _t} = \alpha {\nabla _\theta }\log {\pi _\theta }\left( {{s_t},{a_t}} \right){v_t}\)

蒙特卡洛策略梯度仍然存在较大方差，我们使用评论家来估算行动价值函数，
\({Q_w}\left( {s,a} \right) \approx {Q^{{\pi _\theta }}}\left( {s,a} \right)\)
Actor-Crit算法维护两组参数
Critic:更新动作值函数参数w
Actor:按照评论家的建议更新策略参数θ
参与者评论算法遵循近似策略梯度
\(\begin{array}{l} {\nabla _\theta }J\left( \theta \right) \approx {{\rm E}_{{\pi _\theta }}}\left[ {{\nabla _\theta }\log {\pi _\theta }\left( {s,a} \right){Q_w}\left( {s,a} \right)} \right] \\ \Delta \theta = \alpha {\nabla _\theta }\log {\pi _\theta }\left( {s,a} \right){Q_w}\left( {s,a} \right) \\ \end{array}\)
评论家正在解决一个熟悉的问题：政策评估
基于行动价值评论者的简单行动者批评算法
使用线性值函数近似。\({Q_w}\left( {s,a} \right) = \phi {\left( {s,a} \right)^{\rm T}}w\)
Critic:通过线性TD(0)更新w
Actor:通过策略梯度更新\(\[\theta \]\)

近似策略梯度会引入偏差，有偏差的策略梯度可能找不到正确的解决方案
幸运的是，如果我们仔细选择值函数近似，这样我们就可以避免引入任何偏差。即我们仍然可以遵循确切的策略梯度。

如果选择w以最小化均方误差，则εw.r.t的斜率。 w必须为零，