强化学习学习笔记（二）-基于模型的动态规划方法

基于模型的动态规划算法

动态规划方法的动态一词指的是问题的顺序或时间组成部分，规划一词指优化一个“程序”，即策略。动态规划是解决复杂问题的一种方法。复杂问题可以分解为很多子问题，解决子问题并把这些子问题结合一起。
动态规划假定完全了解MDP，即已知环境模型。可以用于一个MDP的规划。

动态规划（DP）一词是指一组算法，这些算法可用于在给定环境完美模型作为马尔可夫决策过程（MDP）的情况下计算最佳策略。经典的DP算法在强化学习中的作用有限，这既是因为它们假设了一个完美的模型，又是因为它们的计算量很大，但是它们在理论上仍然很重要。DP为理解本书其余部分中介绍的方法提供了必要的基础。 实际上，所有这些方法都可以看作是试图实现 与DP几乎相同的效果，只是需要较少的计算，而无需假设理想的环境模型。
从本章开始，我们通常假设环境是有限的MDP。尽管DP方法可以应用于具有连续状态和动作空间的问题，但是只有在特殊情况下才可能提供精确的解决方案。 DP的关键思想以及一般情况下的强化学习的关键思想是利用价值函数来组织和构造对良好策略的搜索。 在本章中，我们说明如何使用DP来计算第3章中定义的值函数。如此处所讨论的，一旦找到满足Bellman最优函数的最优价值函数\({v_*}\)或\({q_*}\)，就可以轻松获得最优策略。
\(\begin{array}{l} {v_*}(s) = \mathop {\max }\limits_a {\rm E}\left[ {{R_{t + 1}} + \gamma {v_*}({S_{t + 1}})\left| {{S_t} = s,{A_t} = a} \right.} \right] \\ = \mathop {\max }\limits_a \sum\limits_{s',r} {p\left( {s',r|s,a} \right)\left[ {r + \gamma {v_*}(s')} \right]} , \\ or \\ {q_*}\left( {s,a} \right) = {\rm E}\left[ {{R_{t + 1}} + \gamma \mathop {\max }\limits_{a'} {q_{\rm{*}}}\left( {{S_{t + 1}},a'} \right)|{S_t} = s,{A_t} = a} \right] \\ = \sum\limits_{s',r} {p\left( {s',r|s,a} \right)\left[ {r + \gamma \mathop {\max }\limits_{a'} {q_*}(s',a')} \right]} , \\ \end{array}\)
正如我们将看到的，DP算法是通过将诸如此类的Bellman方程转化为赋值，即转化为用于改善所需值函数的近似值的更新规则而获得的。

策略评估

首先，我们考虑如何为任意策略$\pi \(计算状态值函数\){v_\pi }$。

\(\begin{array}{l} {v_\pi }\left( s \right)\dot = {{\rm E}_\pi }\left[ {{G_t}\left| {{S_t} = s} \right.} \right] = {{\rm E}_\pi }\left[ {{R_{t + 1}} + \gamma {G_{t + 1}}\left| {{S_t} = s} \right.} \right] \\ = {{\rm E}_\pi }\left[ {{R_{t + 1}} + \gamma {v_\pi }\left( {{S_{t + 1}}} \right)\left| {{S_t} = s} \right.} \right] \\ = \sum\limits_a {\pi \left( {a\left| s \right.} \right)} \sum\limits_{s',r} {p\left( {s',r\left| {s,a} \right.} \right)} \left[ {r + \gamma {v_\pi }\left( {s'} \right)} \right] \\ \end{array}\)

\(\begin{array}{l} {v_{k + 1}}\left( s \right)\dot = {{\rm E}_\pi }\left[ {{R_{t + 1}} + \gamma {v_k}\left( {{S_{t + 1}}} \right)\left| {{S_t} = s} \right.} \right] \\ = \sum\limits_a {\pi \left( {a\left| s \right.} \right)} \sum\limits_{s',r} {p\left( {s',r\left| {s,a} \right.} \right)} \left[ {r + \gamma {v_k}\left( {s'} \right)} \right], \\ \end{array}\)

如图所示为策略评估算法的伪代码。需要注意的是，在每次迭代中都需要对状态集进行一次遍历（扫描）以便评估每个状态的值函数。
接下来，我们举个策略评估的例子。如图所示为网格世界，其状态空间为：\(S = \left\{ {1,2, \cdots ,14} \right\}\)，动作空间A={东，南，西，北}，回报函数为r=-1。需要评估的策略为均匀随机策略，即每个动作的概率均为0.25。

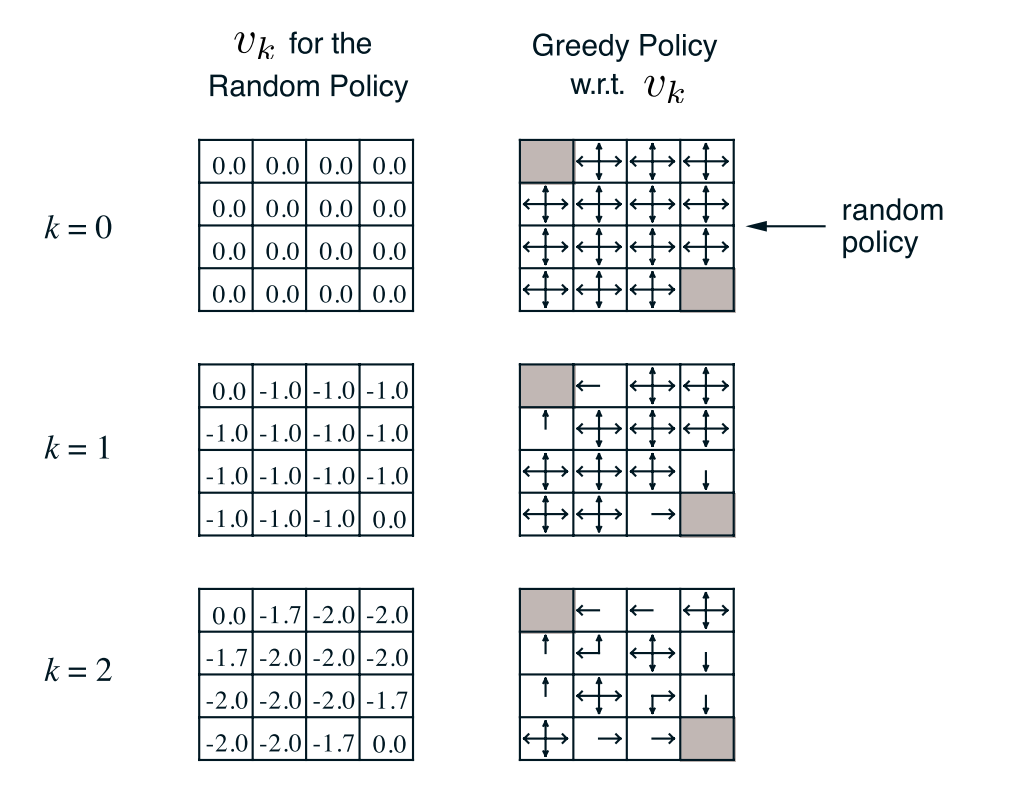
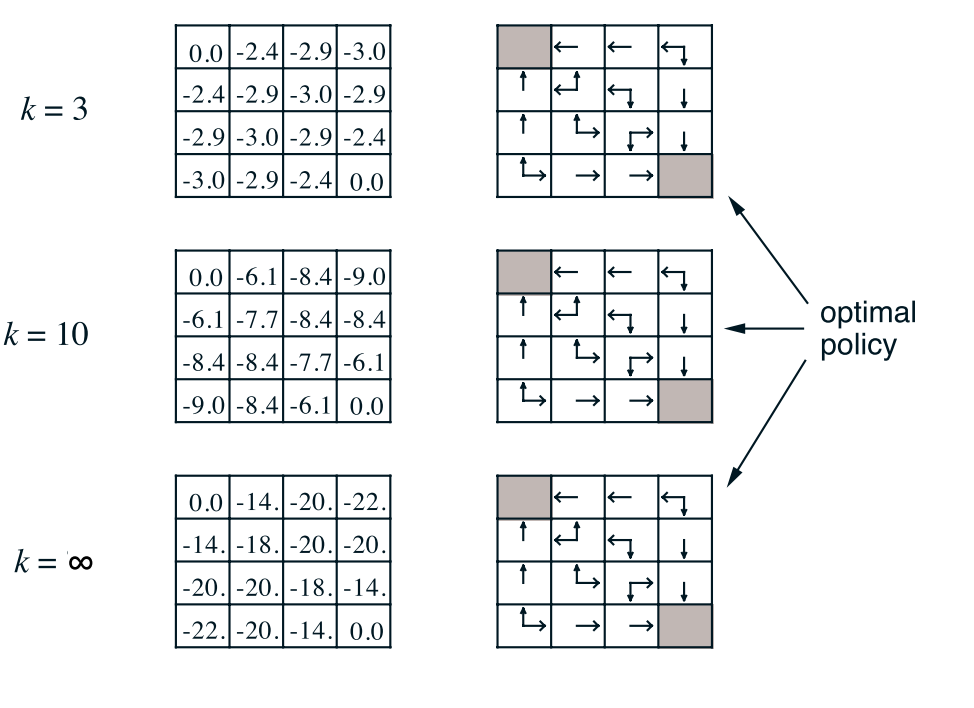
上图为值函数迭代过程值函数的变化。为了进一步说明，我们举个具体的例子，比如从K=1到K=2时，状态1处的值函数计算过程
策略改进
我们计算策略的价值函数的原因是为了帮助找到更好的策略。在DP文献中，这称为策略评估。 我们也将其称为预测问题。
由更新公式得：
\({v_2}(1) = 0.25*\left( {{\rm{ - 1 - 1}}} \right){\rm{ + 0}}{\rm{.25*}}\left( {{\rm{ - 1 - 1}}} \right){\rm{ + 0}}{\rm{.25*}}\left( { - 1 - 1} \right) + 0.25*\left( {0 - 1} \right) = - 1.75\)
保留两位有效数字便是-1.7。

策略迭代

计算值函数的目的是利用值函数找到最优策略。第二个要解决的问题是：如何利用值函数进行策略改善，从而得到最优策略。
一个很自然的方法是当已知当前策略的值函数时，在每个状态采用贪婪策略对当前策略进行改进，即：
\({\pi _{l + 1}}\left( s \right) \in \mathop {\arg \max }\limits_a {q^{{\pi _l}}}\left( {s,a} \right)\)

上图是方格世界谈论策略的示意图。我们仍然以状态1为例得到改进的贪婪策略：
\(\begin{array}{l} {\pi _1}\left( 1 \right) = \mathop {\arg \max }\limits_a \left\{ {q\left( {1,n} \right),q\left( {1,e} \right),q\left( {1,s} \right),q\left( {1,w} \right)} \right\} \\ = \mathop {\arg \max }\limits_a \left\{ { - 1 - 8.4, - 1 - 7.7, - 1{\rm{ + 0, - 1 - 6}}{\rm{.1}}} \right\}{\rm{ = }}\left\{ w \right\} \\ \end{array}\)
至此，我们已经给出了策略评估和策略改进算法。万事已具备，将策略评估算法和策略改进算法组合起来便组成了策略迭代算法。

值迭代

策略迭代的一个缺点是其每次迭代都涉及策略评估，策略评估本身可能是旷日持久的迭代计算，需要对状态集进行多次扫描。如果策略评估是反复进行的，则仅在极限内才发生与v⇡的精确收敛。我们必须等待精确的收敛，还是可以停止收敛？ 图4.1中的示例肯定表明，有可能截断策略评估。 在该示例中，超过前三个的策略评估迭代对相应的贪婪策略没有影响。
实际上，可以以几种方式截断策略迭代的策略评估步骤，而不会丢失策略迭代的收敛性保证。一种重要的特殊情况是，仅一次扫描（每个状态一次更新）后就停止了策略评估。 此算法称为值迭代。 它可以写为一种特别简单的更新操作，将策略改进和缩短的策略评估步骤结合在一起：

价值迭代有效地将策略评估的一次扫描和策略改进的一次扫描结合在一起。通常，可以通过在每个策略改进扫描之间插入多个策略评估扫描来实现更快的收敛。 通常，可以将整类的截断策略迭代算法视为一系列扫描，其中一些使用策略评估更新，而另一些使用值迭代更新。因为（4.10）中的最大操作是这些更新之间的唯一区别，所以这仅意味着将最大操作添加到某些策略评估扫描中。 所有这些算法都收敛到折扣有限MDP的最优策略。