第三单元总结
关于自测
- 我的构造数据主要是根据
JML规格里构造相应的测试数据的,针对于一个函数或者一条指令来构造相应的函数,我也想过写一个数据生成器,但后来发现根据JML规格来进行一些测试貌似更加方便一些,于是便开始了Junit测试。这样可以使得数据尽可能得覆盖到所有的情况。当然这也只适合一些基础的测试(但往往把基础的函数写好了,后面一般不会出现大问题)。当然我还采用了跟其他同学对拍的方法进行测试,这也发现了我的一些bug(啪啪打脸)主要的测试流程也就是这些了。
架构分析
并查集
- 第九次作业主要是有一个
qbs以及一个qci,涉及到判断两个点是否连通、判断有几个连通块的问题。考虑到使用dfs非常有可能会超时(即使过了强测,也躲不过互测),因此我采用了并查集 + 路径压缩的方式进行优化,并在优化过程中维护连通块的数目,这就大大缩短了询问时间,无疑是很好的选择。同时考虑到如果说就以personId存储在数组中的话会很浪费资源并且为了便于维护,解决方法是:每添加一个元素,就新建立一个映射,这样充分利用了数组资源,缺点便是这样debug时会不太方便查看是哪个person出了错。
public void addElement(int x) {
map.put(x, size);
size++;
father[map.get(x)] = map.get(x);
setNumber++;
}
public void union(int x, int y) {
int root1 = find(x);
int root2 = find(y);
father[root1] = root2;
if (root1 != root2) {
setNumber--;
}
}
public int find(int x) {
if (x != father[x]) {
father[x] = find(father[x]);
}
return father[x];
}
- 这次架构不足之处便是没有把关于并查集的部分封装成一个类,是我的架构不足之处。
Kruskal
- 第十次作业中的
qlc指令是要寻找某个节点的最小生成树的权值,考虑到并查集可以优化时间,于是我采用了Kruskal算法并使用并查集进行了优化。
public class Kruskal {
private final DisjointSet disjointSet;
private final ArrayList<Edge> edges;
public Kruskal(ArrayList<Edge> edges) {
this.edges = edges;
disjointSet = new DisjointSet();
}
public int run() {
ArrayList<Edge> edges1 = new ArrayList<>();
int min = 0;
for (Edge edge : edges) {
int st = edge.getSt();
int end = edge.getEnd();
int value = edge.getValue();
if (!disjointSet.getMap().containsKey(st)) {
disjointSet.addElement(st);
}
if (!disjointSet.getMap().containsKey(end)) {
disjointSet.addElement(end);
}
int root1 = disjointSet.find(disjointSet.getMap().get(st));
int root2 = disjointSet.find(disjointSet.getMap().get(end));
if (root1 != root2) {
edges1.add(edge);
disjointSet.union(disjointSet.getMap().get(st), disjointSet.getMap().get(end));
min += value;
}
}
// for debug
/*
for (Edge edge : edges1) {
System.out.println("the st is: " + edge.getSt() +
", the end is: " + edge.getEnd() + ", the weight is: " + edge.getValue());
}*/
return min;
}
}
- 这次架构的不足之处大家也可以从上面的代码中看不出来吗,其实我当时写的时候并没有新建并查集的类,而是把那些方法复制了一遍过来,这个问题在第十一次作业我
checkstyle没过时才想到了可以这样做,看来checkstyle还是很有用滴!!!
- 另外此次作业中
group的一些查询方法需要注意,这些方法的复杂度是O(n^2),如果不实时维护该变量的话,指令稍微过多便很有可能会超时(笔者这里就错了
PriorityQueue
- 第十一次作业中的
sim是将消息发送给没有直接关系的两者并且要求是最短路径,这次我采用了Dijkstra算法,一开始并没有进行优化,后来经过计算复杂度发现不进行堆优化很有可能会超时,PriorityQueue会自动进行堆排序,并且每次poll出来的都是最小的元素,于是采用了PriorityQueue进行优化,不得不说实在是太方便了。
public int dijkstraOptimize(int st, int end) {
int[] result = new int[people.size()];
boolean[] visit = new boolean[people.size()];
PriorityQueue<Edge> myQueue = new PriorityQueue<>();
myQueue.add(new Edge(st, st, 0));
for (int i = 0; i < people.size(); i++) {
visit[i] = false;
result[i] = Integer.MAX_VALUE;
}
// System.out.println("the st is " + st + " the end is " + end);
while (!myQueue.isEmpty()) {
Edge minEdge = myQueue.poll();
int idx = minEdge.getEnd();
int min = minEdge.getValue();
visit[idx] = true;
result[idx] = min;
if (idx == end) {
break;
}
// System.out.println("the select point is: " + idx);
// System.out.println("the min distance is " + min);
for (Edge edge : table.get(idx)) {
int x = edge.getEnd();
int dis = edge.getValue();
if (!visit[x] && min + dis < result[x]) {
result[x] = min + dis;
myQueue.add(new Edge(st, x, min + dis));
}
}
}
/*
for (Integer integer : result.keySet()) {
System.out.println("the key is " + integer + " the value is " + result.get(integer));
}*/
return result[end];
}
- 这次作业我的最大敌人是
checkstyle,因为MyNetWork超了500行,我于是便想着封装一些方法为类,于是便把原来两次作业架构遗忘的并查集架构封装了起来,形成了一个比较好的架构。
性能问题和修复情况
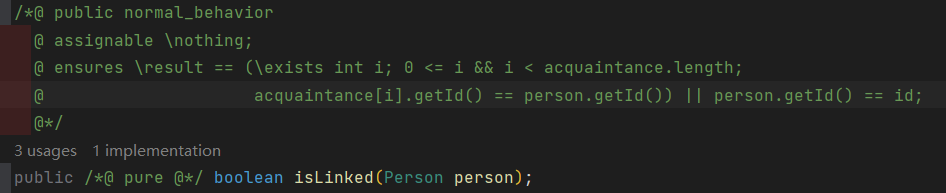
- 第九次作业强测出问题有两个原因,首先在维护连通块的数目是出现了问题,没有判断两点是否已在一个连通块了,直接减1了,导致出现了负数的情况。。。第二个问题就是我没有选择一个好一点的
JML阅读器,就是下面这句话,我看错了括号的位置,导致当查询的Id和personId相同时会返回false,当然下面这个设置是我后来改的,原来的看起来太难受了。。。。
![image]()
- 由于采用了并查集、
Kruskal、PriorityQueue、Dijkstra等方法,并且采用一些便于维护的数据结构,后两次作业强测中没有出现问题,第十次作业互测出问题的原因是qgsv超时,这也是我所没有想到的情况,后添加了一个变量并进行实时维护才修复了此问题。第十二次作业互测没有出现问题。
NetWork拓展
- 假设出现了几种不同的
Person
Advertiser:持续向外发送产品广告Producer:产品生产商,通过Advertiser来销售产品Customer:消费者,会关注广告并选择和自己偏好匹配的产品来购买
- 所谓购买,就是直接通过
Advertiser给相应Producer发一个购买消息
Person:吃瓜群众,不发广告,不买东西,不卖东西
- 如此
Network可以支持市场营销,并能查询某种商品的销售额和 销售路径等
- 请讨论如何对
Network扩展,给出相关接口方法,并选择3个核心 业务功能的接口方法撰写JML规格(借鉴所总结的JML规格模式)
- 三者都应继承于
Peason,并且应当新增一些自身属性,Advertiser新增产品id,并为该产品发送广告,Producer新增产品的数量,代表可以销售的产品,Customer新增reference,代表偏爱的产品,一个product可以有多个producer,但每个producer只能生产一种product
- 发送广告
/*@ public normal_behavior
@ requires containsAdvertisement(advertisementId);
@ assignable advertisements;
@ ensures !containsAdvertisement(advertisementId) && advertisements.length == \old(advertisements.length) - 1 &&
@ (\forall int i; 0 <= i && i < \old(advertisements.length) && \old(advertisements[i].getId()) != advertisementId;
@ (\exists int j; 0 <= j && j < advertisements.length; advertisements[j].equals(\old(advertisements[i]))));
@ ensures (\forall int i; 0 <= i && i < people.length; (people[i].getReference() == advertisementId) ==>
@ (\exists int j; 0 <= j && j < people[i].advertisements.length; people[i].advertisements[j] == advertisementId) &&
@ people[i].advertisements.length == \old(people[i].advertisements.length) + 1);
@ ensures (\forall int i; 0 <= i && i < people.length; !people[i].isFavorable(advertisementId) ==>
@ !(\exists int j; 0 <= j && j < people[i].advertisements.length; people[i].advertisements[j] == advertisementId)) &&
@ people[i].advertisements.length == \old(people[i].advertisements.length));
@ ensures (\forall int i; 0 <= i && i < people.length;
@ (\forall int j; 0 <= j < \old(people[i].advertisements.length)
@ (\exists int k; 0 <= k < people[i].advertisements.length;
@ \old(people[i].advertisements[j]) == people[i].advertisements[k])));
@ also
@ public exceptional_behavior
@ signals (AdvertisementIdNotFoundException e) !containsAdvertisement(advertisementId);
@*/
public void sendAdvertisement(int advertisementId) throws AdvertisementIdNotFoundException;
/*@ public normal_behavior
@ requires contains(customerId) && contains(advertiserId) && containsProduct(getProducer(producerId).getProductId);
@ ensures (getPerson(customerId).getMoney()) = \old((getPerson(customerId).getMoney())) - queryProductPrice(productId);
@ ensures (getProducer(producerId)).getProductNum = \old((getProducer(producerId)).getProductNum) - 1;
@ also
@ public exceptional_behavior
@ signals (PersonIdNotFoundException e) !contains(customerId) || !contains(advertiserId);
@ signals (PersonIdNotFoundException e) contains(customerId) && contains(advertiserId) && !containsProduct(getProducer(producerId).getProductId);
@*/
public void sendPurchaseMessage(int customerId, int advertiserId, int producerId) throws PersonIdNotFoundException, ProductIdNotFoundException;
/*@ public normal_behavior
@ requires contains(producerId)
@ ensures ((Producer) getPerson(producerId)).productNum = \old(((Producer) getPerson(producerId)).productNum) + 1;
@ also
@ public exceptional_behavior
@ signals (PersonIdNotFoundException e) !contains(id);
@*/
public void produceProduct(int producerId) throws PersonIdNotFoundException;
体会与感想
- 这以单元学习了很多关于
JML规格的事情,使得我对于契约式编程有了初步了解,该设计思维在递归设计、函数式编程、约束求解等都有应用。这一单元主要是通过不断迭代最终实现了一个社交模拟网络,可以发送红包、发送表情等功能,难度相比于前两单元下降了一些,但还是会有一些琐碎的bug,这些bug原因都是由于思维不严谨导致的,因此,在往后编程的时候我会更加注重思维的严谨性,同时也会加强自己的测试,非常感谢在这三次作业自测环节陪我一起对拍的小伙伴们。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号