(数据科学学习手札36)tensorflow实现MLP
一、简介
我们在前面的数据科学学习手札34中也介绍过,作为最典型的神经网络,多层感知机(MLP)结构简单且规则,并且在隐层设计的足够完善时,可以拟合任意连续函数,而除了利用前面介绍的sklearn.neural_network中的MLP来实现多层感知机之外,利用tensorflow来实现MLP更加形象,使得使用者对要搭建的神经网络的结构有一个更加清醒的认识,本文就将对tensorflow搭建MLP模型的方法进行一个简单的介绍,并实现MNIST数据集的分类任务;
二、MNIST分类
作为数据挖掘工作中处理的最多的任务,分类任务占据了机器学习的大半江山,而一个网络结构设计良好(即隐层层数和每个隐层神经元个数选择恰当)的多层感知机在分类任务上也有着非常优越的性能,依然以MNIST手写数字数据集作为演示,上一篇中我们利用一层输入层+softmax搭建的分类器在MNIST数据集的测试集上达到93%的精度,下面我们使用加上一层隐层的网络,以及一些tricks来看看能够提升多少精度;
网络结构:
这里我们搭建的多层前馈网络由784个输入层神经元——200个隐层神经元——10个输出层神经元组成,而为了减少梯度弥散现象,我们设置relu(非线性映射函数)为隐层的激活函数,如下图:
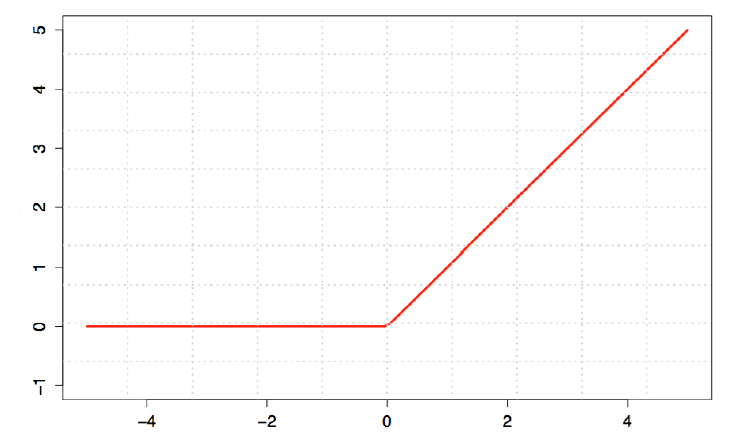
这种激活函数更接近生物神经元的工作机制,即在达到阈值之前持续抑制,在超越阈值之后开始兴奋;而对输出层,因为对数据做了one_hot处理,所以依然使用softmax进行处理;
Dropout:
过拟合是机器学习尤其是神经网络任务中经常发生的问题,即我们的学习器将训练集的独特性质当作全部数据集的普遍性质,使得学习器在训练集上的精度非常高,但在测试集上的精度却非常低(这里假设训练集与测试集数据分布一致),而除了随机梯度下降的一系列方法外(如上一篇中我们提到的在每轮训练中使用全体训练集中一个小尺寸的训练批来进行本轮的参数调整),我们可以使用类似的思想,将神经网络某一层的输出节点数据随机丢弃一部分,即令这部分被随机选中的节点输出值令为0,这样做等价于创造出很多新样本,通过增大样本量,减少特征数量来防止过拟合,dropout也算是一种bagging方法,可以将每次丢弃节点输出视为对特征的一次采样,相当于我们训练了一个ensemble的神经网络模型,对每个样本都做特征采样,并构成一个融合的神经网络
学习效率:
因为神经网络的训练通常不是一个凸优化问题,它充满了很多局部最优,因此我们通常不会采用标准的梯度下降算法,而是采用一些有更大可能跳出局部最优的算法,常用的如SGD,而SGD本身也不稳定,其结果也会在最优解附近波动,且设置不同的学习效率可能会导致我们的网络落入截然不同的局部最优之中,对于SGD,我们希望开始训练时学习率大一些,以加速收敛的过程,而后期学习率低一些,以更稳定地落入局部最优解,因此常使用Adagrad、Adam等自适应的优化方法,可以在其默认参数上取得较好的效果;
下面。就结合上述策略,利用tensorflow搭建我们的多层感知机来对MNIST手写数字数据集进行训练:
2.1 风格一
先使用朴素的风格来搭建网络,首先还是照例从tensorflow自带的数据集中提取出mnist数据集:
import tensorflow as tf from tensorflow.examples.tutorials.mnist import input_data '''导入MNIST手写数据''' mnist = input_data.read_data_sets('MNIST_data/', one_hot = True)
接着使用交互环境下会话的方式,将生成的第一个会话作为默认会话:
'''注册默认的session,之后的运算都会在这个session中进行''' sess = tf.InteractiveSession()
接着初始化输入层与隐层间的784x300个权值、隐层神经元的300个bias、隐层与输出层之间的300x10个权值、输出层的10个bias,其中为了避免隐层的relu激活时陷入0梯度的情况,对输入层和隐层间的权值初始化为均值为0,标准差为0.2的正态分布随机数,对其他参数初始化为0:
'''定义输入层神经元个数''' in_units = 784 '''定义隐层神经元个数''' h1_units = 300 '''为输入层与隐层神经元之间的连接权重初始化持久的正态分布随机数,这里权重为784乘300,300是隐层的尺寸''' W1 = tf.Variable(tf.truncated_normal([in_units, h1_units],mean=0,stddev=0.2)) '''为隐层初始化bias,尺寸为300''' b1 = tf.Variable(tf.zeros([h1_units])) '''初始化隐层与输出层间的权重,尺寸为300X10''' W2 = tf.Variable(tf.zeros([h1_units, 10])) '''初始化输出层的bias''' b2 = tf.Variable(tf.zeros([10]))
接着我们定义自变量、隐层神经元dropout中的保留比例keep_prob的输入部件:
'''定义自变量的输入部件,尺寸为 任意行X784列''' x = tf.placeholder(tf.float32, [None, in_units]) '''为dropout中的保留比例设置输入部件''' keep_prob = tf.placeholder(tf.float32)
接着定义隐层relu激活部分的计算部件、隐层dropout部分的操作部件、输出层softmax的计算部件:
'''定义隐层求解部件''' hidden1 = tf.nn.relu(tf.matmul(x, W1) + b1) '''定义隐层dropout操作部件''' hidden1_drop = tf.nn.dropout(hidden1, keep_prob) '''定义输出层softmax计算部件''' y = tf.nn.softmax(tf.matmul(hidden1_drop, W2) + b2)
还有样本真实分类标签的输入部件以及loss_function部分的计算组件:
'''定义训练label的输入部件''' y_ = tf.placeholder(tf.float32, [None, 10]) '''定义均方误差计算部件,这里注意要压成1维''' loss_function = tf.reduce_mean(tf.reduce_sum((y_ - y)**2, reduction_indices=[1]))
这样我们的网络结构和计算部分全部搭建完成,接下来至关重要的一步就是定义优化器的组件,它会完成自动求导调整参数的工作,这里我们选择自适应的随机梯度下降算法Adagrad作为优化器,学习率尽量设置小一些,否则可能会导致网络的测试精度维持在一个很低的水平不变即在最优解附近来回震荡却难以接近最优解(亲测):
'''定义优化器组件,这里采用AdagradOptimizer作为优化算法,这是种变种的随机梯度下降算法''' train_step = tf.train.AdagradOptimizer(0.18).minimize(loss_function)
接下来就到了正式的训练过程了,我们激活当前会话中所有计算部件,并定义训练步数为15000步,每一轮迭代选择一个批量为100的训练批来进行训练,dropout的keep_prob设置为0.76,并在每50轮训练完成后将测试集输入到当前的网络中计算预测精度,注意在正式预测时dropout的keep_prob应设置为1.0,即不进行特征的丢弃:
'''激活当前session中的全部部件''' tf.global_variables_initializer().run() '''开始迭代训练过程,最大迭代次数为3001次''' for i in range(15000): '''为每一轮训练选择一个尺寸为100的随机训练批''' batch_xs, batch_ys = mnist.train.next_batch(100) '''将当前轮迭代选择的训练批作为输入数据输入train_step中进行训练''' train_step.run({x: batch_xs, y_: batch_ys, keep_prob:0.76}) '''每500轮打印一次当前网络在测试集上的训练结果''' if i % 50 == 0: print('第',i,'轮迭代后:') '''构造bool型变量用于判断所有测试样本与其真是类别的匹配情况''' correct_prediction = tf.equal(tf.argmax(y, 1), tf.argmax(y_, 1)) '''将bool型变量转换为float型并计算均值''' accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32)) '''激活accuracy计算组件并传入mnist的测试集自变量、标签及dropout保留比率,这里因为是预测所以设置为全部保留''' print(accuracy.eval({x: mnist.test.images, y_: mnist.test.labels, keep_prob: 1.0}))
经过全部迭代后,我们的多层感知机在测试集上达到了0.9802的精度表现如下图:
事实上在训练到10000轮左右的时候我们的多层感知机就已经到达这个精度了,说明此时的网络已经稳定在当前的最优解中,后面的训练过程只是在这个最优解附近微弱的震荡而已,所以实际上可以设置更小的迭代轮数;
2.2 风格二
除了上述的将网络结构部件的所有语句一条一条平铺直叙般编写的风格外,还有一种以自编函数来快捷定义网络结构的编程风格广受欢迎,如下:
在添加神经层的时候,我们可以事先编写自编函数如下:
'''自定义神经层添加函数''' def add_layer(inputs, in_size, out_size, activation_function=None): '''定义权重项''' Weights = tf.Variable(tf.random_normal([in_size,out_size])) '''定义bias项''' biases = tf.Variable(tf.zeros([1,out_size]) + 0.1) '''权重与输入值的矩阵乘法+bias项''' Wx_plus_b = tf.matmul(inputs, Weights) + biases '''根据激活函数的设置来处理输出项''' if activation_function is None: outputs = Wx_plus_b else: outputs = activation_function(Wx_plus_b) return outputs
这样就可以用一个函数来代替数条语句,下面我们用这种风格来实现前面同样的功能:
import tensorflow as tf from tensorflow.examples.tutorials.mnist import input_data '''导入MNIST手写数据''' mnist = input_data.read_data_sets('MNIST_data/', one_hot = True) '''自定义神经层添加函数''' def add_layer(inputs, in_size, out_size, activation_function=None): '''定义权重项''' Weights = tf.Variable(tf.truncated_normal([in_size,out_size],mean=0, stddev=0.2)) '''定义bias项''' biases = tf.Variable(tf.zeros([1,out_size]) + 0.1) '''权重与输入值的矩阵乘法+bias项''' Wx_plus_b = tf.matmul(inputs, Weights) + biases '''根据激活函数的设置来处理输出项''' if activation_function is None: outputs = Wx_plus_b else: outputs = activation_function(Wx_plus_b) return outputs '''创建样本数据和dropout参数的输入部件''' x = tf.placeholder(tf.float32, [None, 784]) y = tf.placeholder(tf.float32, [None, 10]) keep_prob = tf.placeholder(tf.float32) '''利用自编函数来生成隐层的计算部件,这里activation_function设置为relu''' l1 = add_layer(x, 784,300, activation_function=tf.nn.relu) '''对l1进行dropout处理''' l1_dropout = tf.nn.dropout(l1,keep_prob) '''利用自编函数对dropout后的隐层输出到输出层输出创建计算部件,这里将activation_function改成softmax''' prediction = add_layer(l1_dropout, 300, 10, activation_function=tf.nn.softmax) '''根据均方误差构造loss function计算部件''' loss = tf.reduce_mean(tf.reduce_sum((prediction - y)**2, reduction_indices=[1])) '''定义优化器部件''' train_step = tf.train.AdagradOptimizer(0.3).minimize(loss) '''激活所有部件''' init = tf.global_variables_initializer() '''创建新会话''' sess = tf.Session() '''在新会话中激活所有部件''' sess.run(init) '''10001次迭代训练,每200次输出一次当前网络在测试集上的精度''' for i in range(10001): '''每次从训练集中抽出批量为200的训练批进行训练''' x_batch,y_batch = mnist.train.next_batch(200) '''激活sess中的train_step部件''' sess.run(train_step, feed_dict={x:x_batch, y:y_batch, keep_prob:0.75}) '''每200次迭代打印一次当前精度''' if i %200 == 0: print('第',i,'轮迭代后:') '''创建精度计算部件''' whether_correct = tf.equal(tf.argmax(y, 1), tf.argmax(prediction, 1)) accuracy = tf.reduce_mean(tf.cast(whether_correct, tf.float32)) '''在sess中激活精度计算部件来计算当前网络的精度''' print(sess.run(accuracy, feed_dict={x:mnist.test.images, y:mnist.test.labels, keep_prob:1.0}))
同样的,在10000次迭代后,我们的单隐层前馈网络取得了0.98的精度:
以上就是关于tensorflow搭建MLP模型的基本内容,如有笔误,望指出。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号