（数据科学学习手札35）tensorflow初体验

一、简介

　　TensorFlow时谷歌于2015年11月宣布在Github上开源的第二代分布式机器学习系统，目前仍处于快速开发迭代中，有大量的新功能新特性在陆续研发中；

　　TensorFlow既是一个实现机器学习算法的接口，同时也是执行机器学习算法的框架。它的前端支持Python、C++、Go、Java等多种开发语言，后端使用C++、CUDA等编写，其实现的算法可以在很多不同的系统上进行移植，虽然TensorFlow主要用来执行的是深度学习算法，但其也可以用来实现很多其他算法，诸如线性回归、逻辑回归、随机森林等，目前，TensorFlow依然成为最流行的深度学习框架；

　　TensorFlow的特点是它使用数据流式图来进行计算流程的规划，其内部的计算都可以表示为一个有向图（directed graph），或称计算图（computation graph），其中每一个运算操作（operation）将作为一个节点（node），而节点之间的连接称为边（edge），通过这个规划好的计算图，很清楚的描述了数据的计算流程，它也负责维护和更新状态，用户可以对计算图的分支进行条件控制或循环操作。用户可以使用Python、C++、Go、Java等几种语言设计这个数据计算的有向图。计算图的每一个结点都可以有任意多个输入和任意多个输出，每一个节点描述了一种运算操作，节点相当于运算操作的实例化（instance）。

　　而对于tensorflow完成实际学习任务时的工作机制的介绍，下面以一个广为人知的分类任务为引；

 

二、MNIST手写数字识别

　　作为机器学习中hello world级别的案例，MNIST是一个非常简单的计算机视觉数据集，它由数万张28X28像素的手写数字图片组成，这些图片只包含灰度值信息，而我们的训练任务是实现对这些数字进行分类至0-9一共10类，tensorflow和sklearn一样自带了这个数据集，并且已经分成55000个训练集样本，10000个测试集样本，以及5000个验证集样本，每个样本有28X28=784个维度特征作为自变量，即已经将图片展开成一行（本篇只是对tensorflow进行一个基本的初探，关于结构化数据的处理之后的博文会介绍），以及一个数字做为因变量，即其真实代表的数字，我们载入这个数据集中训练集、验证集与测试集，并对因变量进行one hot处理，即用一个10维的向量来代替原来的因变量，譬如，真实数字为0，则它one hot编码后的结果为[1,0,0,0,0,0,0,0,0,0]，即除了它真实数值所在的位置，其他位置全为0；并且我们随意挑选绘制其中的一个样本：

import matplotlib.pyplot as plt
from tensorflow.examples.tutorials.mnist import input_data

'''载入MNIST数据集，并进行one hot处理'''
mnist = input_data.read_data_sets('MNIST_data',one_hot=True)

'''抽出训练集中的一行出来并reshape为28X28的形式'''
test = mnist.train.images[666,:].reshape([28,28])

'''绘制格点图'''
plt.matshow(test)

运行结果：

我们一眼就能看出这是个5，接下来我们利用tensorflow训练模型来实现机器对其的分类，这里因为是初探tensorflow的演示，故不选择进阶的复杂模型，而是采用softmax regression算法，这是一个经典的处理多分类问题的算法，softmax函数会对每一种类别输出的概率进行估算，然后选取其中最大的那个作为正式输出，是神经网络中多分类模型的基础，其基础的解释如下，更细致的解析将会在下一篇博文中介绍：

Softmax Regression：

　　对我们前面提到的one hot的结果，即转换后的10个特征，用i代表第i个类，j代表一个样本的第i个自变量特征即第i个像素点，bias表示数据集本身的倾向，类似先验分布，有如下式子：

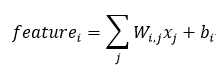
 接着，经过前面的加权加偏移的输入过程，就到了softmax的部分，对于前面传入的每一个feature，先经过：

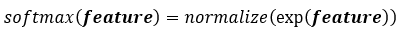
即对每一个位置的输入特征进行指数化（将非正数正数化）再进行标准化（使得所有输出相加等于1，即对每个特征输入指数化后的结果施加一个伸缩系数），再于是得到每个特征位置输出的概率值：

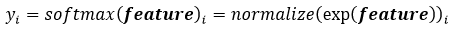
将上述的过程转化为矩阵乘法形式（这里指的是单个样本的计算过程）即为：

 

 即

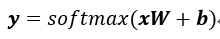
理清楚上面这个过程，下面就来利用tensorflow搭建一系列部件来实现softmax regression，因为Python本身运算效率不高，因此为了加速运算，tensorflow在利用Python语句搭建好计算图结构后，运行时将计算部分利用C++放在CPU中或利用CUDA运行在GPU上，我们首先载入tf库，并创建一个新的InteractiveSession作为默认的session，之后的运算在不更改session的情况都在该session中运行：

import tensorflow as tf

'''注册默认的session，之后的运算都会在这个session中进行'''
sess = tf.InteractiveSession()

接着我们创建一个placeholder对象作为自变量的入口，这是tensorflow中用于输入数据的部件，其中的第一个参数指定的传入数据的精度类型，第二个列表形式的参数指定了该数据入口允许的数据集形状（行数、列数），行设置为None表示输入的样本数没有限制，但输入数据的特征维数一定是784个：

'''创建placeholder用来定义数据的入口部件，其中第一个参数设置数据类型，第二个参数控制输入数据的shape，None表示样本数不限，784列表示特征维度限制为784维'''
x = tf.placeholder(tf.float32, [None, 784])

接下来要为模型中逐轮调整的参数创建容器，tensorflow中的variable对象就是专门为模型的参数设置的容器部件，不同于存储数据的tensor一经使用便马上消失，variable在模型的训练过程中是一直存在的，并且模型训练完成后还可以被导出，它们在每一轮迭代中被更新，这里我们将weights和biases全部初始化为0，因为这里的演示比较简单，真实的训练任务中往往会利用少量数据进行预训练以确定一个较好的weights和biases起点，按照我们之前推导的公式，则W的形状为784X10，biases的形状为1X10：

'''为权重和bias设置持久化的variable，这里权重为784乘10,10是输出层的尺寸'''
W = tf.Variable(tf.zeros([784,10]))

b = tf.Variable(tf.zeros([10]))

初始化所有参数后，下面要进行的就是对softmax函数计算部分部件的初始化，我们使用tensorflow.nn中的softmax()组件，tensorflow.nn用于存放各种神经网络组件，我们在softmax求解器中按照前面的计算公式部署我们前面所有参数及变量，tf.matmul()表示tf中的矩阵乘法：

'''定义输出层softmax求解部件'''
y = tf.nn.softmax(tf.matmul(x, W) + b)

所有计算图中forward的部分基本完成，下面要为BP算法来设置一个loss function，考虑这样一个例子：

对于某个样本的真实值y和某轮算法的输出值y’（这里均指one hot后的形式）：

 

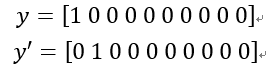
可以看出，算法的估计值并没有完美达到真实值y，因此基于均方误差的思想，构造loss function如下：

 

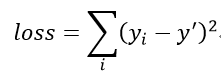
则我们的训练目标即BP算法优化的方向是一轮一轮地削减这个loss function，因此我们将训练样本真实的标签也设置一个入口部件，并在loss function中进行计算，对应的代码如下：

'''将均方误差作为loss function来描述模型的分类精度'''

'''定义均方误差求解的计算入口部件,y_代表真实类别'''
y_ = tf.placeholder(tf.float32, [None, 10])

'''根据均方误差的计算公式定义计算部件'''
loss_function = tf.reduce_mean((y_ - y)**2)

现在我们有了模型，有了loss function，接下来需要的就是根据梯度进行求解的优化器了，这里我们选择比价简单的标准梯度下降算法，tf.train中集成了很多优化器，这里我们选择梯度下降法对应的tf.train.GradientDescentOptimizer：

'''定义优化器组件，这里采用标准的梯度下降法作为优化算法'''
train_step = tf.train.GradientDescentOptimizer(0.5).minimize(loss_function)

至此，我们所有的训练计算图部分都已经搭建好，下面需要激活所有计算图，并进行迭代，我们对全局参数初始化器tf.global_variables_initializer()使用run()方法，：

'''使用全局参数初始化器并进行run'''
tf.global_variables_initializer().run()

这样我们的计算图就搭建好了，下面通过循环迭代进行前面定义的train_step，设定最大迭代次数，以及要feed给模型的各项输入即可，这里我们为了收敛更快且以更大的可能跳出局部最优，每一轮迭代从总的训练集中抽出100个样本进行训练，这就相当于随机梯度下降，我们使用next_batch()来实现这个抽样的过程，并对train_step施加run方法，传入参数为字典指定的自变量与因变量，具体代码如下：

'''迭代执行训练操作'''
for i in range(10000):
    batch_xs, batch_ys = mnist.train.next_batch(100)
    train_step.run({x:batch_xs, y_:batch_ys})

这样经过些许等待，我们就可以得到10000次迭代后的模型，下面利用测试集对其准确率进行考察，还是像以前一样，先搭建涉及到的计算图，再feed数据，这里的eval()和Session.run()的效用是等价的，就是激活计算图：

'''判断预测值与真实值是否相等并保存到bool型变量中'''
correct_prediction = tf.equal(tf.argmax(y, 1), tf.argmax(y_, 1))

'''统计正确率，这里tf.cast用来将bool型变量转化为float32，再求平均值，即正确率'''
accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))

print(accuracy.eval({x:mnist.test.images, y_:mnist.test.labels}))

运行结果：

但不要觉得0.93了挺不错的，实际上早在上个世纪90年代就已经利用LeNet5实现了在MNIST数据集上99%的正确率，因为我们本文只是简单初体验一下tensorflow，并没有对MNIST的图片结构信息有什么利用；

　　我们将上述过程概括一下，主要有以下几个核心步骤：

　　1、初始化session，定义算法中，在神经网络里是forward的计算部分计算图部件；

　　2、定义loss function、优化器以及优化器优化loss的计算图部件；

　　3、激活所有部件，并在循环中自定义数据的feed方式进行训练；

　　4、在测试集上利用训练好的模型来计算各种评价指标；

 

三、现状

　　自从2006年Hinton等人提出了逐层预训练来初始化权重的方法，以及利用多层RBM（受限玻尔兹曼机，Restricted Boltzmann Machine，一种基于分布的神经网络）堆叠成了DBN（深度信念网络，Deep Belief Network）神经网络后，人们又对神经网络赋予了极大的期待，大量新结构的神经网络也应孕而生，神经网络的最大价值在于对特征的自动提取和抽象，免去了人工做特征工程的繁琐，可以自动找出复杂且有效的高阶特征，这一点类似人的学习过程，对知识的理解从浅入深，神经网络的隐层越多，能够提取到的特征就更抽象；

　　当下，深度学习在复杂机器学习问题上的碾压性优势已经确定，只要有足够多数据，设计完善的神经网络都可以取得比其他算法更好的效果，其实本篇中的模型可以算是一个没有隐层的神经网络，而在之后的文章中，我将就一些流行的更加复杂的神经网络进行介绍，敬请期待。