(数据科学学习手札26)随机森林分类器原理详解&Python与R实现
一、简介
作为集成学习中非常著名的方法,随机森林被誉为“代表集成学习技术水平的方法”,由于其简单、容易实现、计算开销小,使得它在现实任务中得到广泛使用,因为其来源于决策树和bagging,决策树我在前面的一篇博客中已经详细介绍,下面就来简单介绍一下集成学习与Bagging;
二、集成学习
集成学习(ensemble learning)是指通过构建并结合多个学习器来完成学习任务,有时也被称为多分类器系统(multi-classifier system)等;
集成学习的一般结构如下:
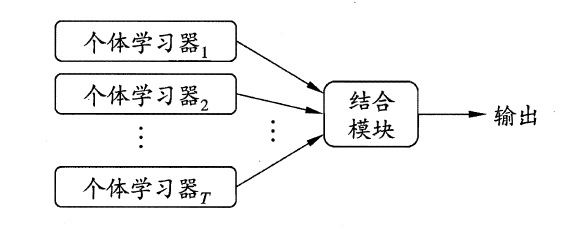
可以看出,集成学习的一般过程就是先产生一组“个体学习器”(individual learner),再使用某种策略将这些学习器结合起来。个体学习器通常由一个现有的学习算法从训练数据产生,例如C4.5决策树算法,BP神经网络算法等,此时集成中只包含同种类型的个体学习器,譬如“决策树集成”纯由若干个决策树学习器组成,这样的集成是“同质”(homogeneous),同质集成中的个体学习器又称作“基学习器”(base learner),相应的学习算法称为“基学习算法”(base learning algorithm)。集成也可以包含不同类型的个体学习器,例如可以同时包含决策树与神经网络,这样的集成就是“异质”的(heterogenous),异质集成中的个体学习器由不同的学习算法组成,这时不再有基学习算法;对应的,个体学习器也不再称作基学习器,而是改称为“组件学习器”(component learner)或直接成为个体学习器;
集成学习通过将多个学习器进行结合,常可获得比单一学习器更加显著优越的泛化性能,尤其是对“弱学习器”(weak learner),因此集成学习的很多理论研究都是针对弱学习器来的,通过分别训练各个个体学习器,预测时将待预测样本输入每个个体学习器中产出结果,最后使用加权和、最大投票法等方法将所有个体学习器的预测结果处理之后得到整个集成的最终结果,这就是集成学习的基本思想;
三、Bagging
通过集成学习的思想,我们可以看出,想要得到泛化性能强的集成,则集成中的个体学习器应当尽可能相互独立,但这在现实任务中几乎无法实现,所以我们可以通过尽可能增大基学习器间的差异来达到类似的效果;一方面,我们希望尽可能增大基学习器间的差异:给定一个数据集,一种可能的做法是对训练样本进行采样,分离出若干个子集,再从每个子集中训练出一个基学习器,这样我们训练出的各个基学习器因为各自训练集不同的原因就有希望取得比较大的差异;另一方面,为了获得好的集成,我们希望个体学习器的性能不要太差,因为如果非要使得采样出的每个自己彼此不相交,则由于每个子集样本数量不足而无法进行有效学习,从而无法确保产生性能较好的个体学习器,为了解决这矛盾的问题,Bagging应运而生;
Bagging是并行式集成学习方法最著名的代表,它基于自助采样法(bootstrap sampling),对给定包含m个样本的数据集,我们先随机取出一个样本放入采样集中,再把该样本放回初始数据集,即一次有放回的简单随机抽样,这样重复指定次数的抽样,得到一个满足要求的采样集合,且样本数据集中的样本有的在该采样集中多次出现,有的则从未出现过,我们可以将那些没有在该采样集出现过的样本作为该采样集对应训练出的学习器的验证集,来近似估计该个体学习器的泛化能力,这被称作“包外估计”(out-of-bag estimate),令Dt表示第t个个体学习器对应的采样集,令Hoob(x)表示该集成学习器对样本x的包外预测,即仅考虑那些未使用x训练的学习器在x上的预测表现,有:
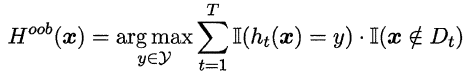
则Bagging泛化误差的包外估计为:

而且包外样本还可以在一些特定的算法上实现较为实用的功能,例如当基学习器是决策树时,可使用保外样本来辅助剪枝,或用于估计决策树中各结点的后验概率以辅助对零训练样本节点的处理;当基学习器是神经网络时,可以用包外样本来辅助进行早停操作;
四、随机森林
随机森林(Random Forest)是Bagging的一个扩展变体。其在以决策树为基学习器构建Bagging集成的基础上,进一步在决策树的训练过程中引入了随机属性选择,即:传统决策树在选择划分属性时是在当前结点的属性集合中(假设共有d个结点)基于信息纯度准则等选择一个最优属性,而在随机森林中,对基决策树的每个结点,先从该结点的属性集合中随机选择一个包含k个属性的子集,再对该子集进行基于信息准则的划分属性选择;这里的k控制了随机性的引入程度;若令k=d,则基决策树的构建与传统决策树相同;若令k=1,则每次的属性选择纯属随机,与信息准则无关;一般情况下,推荐k=log2d。

随机森林对Bagging只做了小小的改动,但是与Bagging中基学习器的“多样性”仅通过样本扰动(即改变采样规则)不同,随机森林中基学习器的多样性不仅来自样本扰动,还来自属性扰动,这就使得最终集成的泛化性能可通过个体学习器之间差异度的增加而进一步提升;
随机森林的收敛性与Bagging类似,但随机森林在基学习器数量较为可观时性能会明显提升,即随着基学习器数量的增加,随机森林会收敛到更低的泛化误差;
五、Python实现
我们使用sklearn.ensemble中的RandomForestClassifier()来进行随机森林分类,其细节如下:
常用参数:
n_estimator:整数型,控制随机森林算法中基决策树的数量,默认为10,我建议取一个100-1000之间的奇数;
criterion:字符型,用来指定做属性划分时使用的评价准则,'gini'表示基尼系数,也就是CART树,'entropy'表示信息增益;
max_features:用来控制每个结点划分时从当前样本的属性集合中随机抽取的属性个数,即控制了随机性的引入程度,默认为'auto',有以下几种选择:
1.int型时,则该传入参数即作为max_features;
2.float型时,将 传入数值*n_features 作为max_features;
3.字符串时,若为'auto',max_features=sqrt(n_features);'sqrt'时, 同'auto';'log2'时,max_features=log2(n_features);
4.None时,max_features=n_features;
max_depth:控制每棵树所有预测路径的长度上限(即从根结点出发经历的划分属性的个数),建议训练时该参数从小逐渐调大;默认为None,此时每棵树只有等到所有的叶结点中都只存在一种类别的样本或结点中样本数小于min_samples_split时化成叶结点时该预测路径才停止生长;
min_samples_split:该参数控制当结点中样本数量小于某个整数k时将某个结点标记为叶结点(即停止该预测路径的生长),传入参数即控制k,当传入参数为整数时,该参数即为k;当传入参数属于0.0~1.0之间时,k=传入参数*n_samples;默认值为2;
max_leaf_nodes:控制每棵树的最大叶结点数量,默认为None,即无限制;
min_impurity_decrease:控制过拟合的一种措施,传入一个浮点型的数,则在每棵树的生长过程中,若下一个节点中的信息纯度与上一个结点中的节点纯度差距小于这个值,则这一次划分被剪去;
booststrap:bool型变量,控制是否采取自助法来划分每棵树的训练数据(即每棵树的训练数据间是否存在相交的可能),默认为True;
oob_score:bool型变量,控制是否用包外误差来近似学习器的泛化误差;
n_jobs:控制并行运算时的核心数,默认为单核即1,特别的,设置为-1时开启所有核心;
random_rate:设置随机数种子,目的是控制算法中随机的部分,默认为None,即每次运行都是随机地(伪随机);
class_weight:用于处理类别不平衡问题,即为每一个类别赋权,默认为None,即每个类别权重都为1;'balanced'则自动根据样本集中的类别比例为算法赋权;
函数输出项:
estimators_:包含所有训练好的基决策树细节的列表;
classes:显示所有类别;
n_classes_:显示类别总数;
n_features_:显示特征数量(训练之后才有这个输出项);
feature_importances_:显示训练中所有特征的重要程度,越大越重要;
oob_score_:学习器的包外估计得分;
下面我们以sklearn.datasets自带的威斯康辛州乳腺癌数据作为演示数据,具体过程如下:
from sklearn.ensemble import RandomForestClassifier from sklearn.model_selection import train_test_split from sklearn.metrics import f1_score as f1 from sklearn.metrics import confusion_matrix as con from sklearn import datasets ###载入威斯康辛州乳腺癌数据 X,y = datasets.load_breast_cancer(return_X_y=True) ###分割训练集与测试集 X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.3) ###初始化随机森林分类器,这里为类别做平衡处理 clf = RandomForestClassifier(class_weight='balanced',random_state=1) ###返回由训练集训练成的模型对验证集预测的结果 result = clf.fit(X_train,y_train).predict(X_test) ###打印混淆矩阵 print('\n'+'混淆矩阵:') print(con(y_test,result)) ###打印F1得分 print('\n'+'F1 Score:') print(f1(y_test,result)) ###打印测试准确率 print('\n'+'Accuracy:') print(clf.score(X_test,y_test))
运行结果如下:

可以看出,随机森林的性能十分优越。
六、R实现
在R语言中我们使用randomForest包中的randomForest()函数来进行随机森林模型的训练,其主要参数如下:
formula:一种 因变量~自变量 的公式格式;
data:用于指定训练数据所在的数据框;
xtest:randomForest提供了一种很舒服的(我窃认为)将训练与验证一步到位的体制,这里xtest传入的就是验证集中的自变量;
ytest:对应xtest的验证集的label列,缺省时则xtest视为无标签的待预测数据,这时可以使用test$predicted来调出对应的预测值(实在是太舒服了);
ntree:基决策树的数量,默认是500(R相当实在),我建议设定为一个大小比较适合的奇数;
classwt:用于处理类别不平衡问题,即传入一个包含因变量各类别比例的向量;
nodesize:生成叶结点的最小样本数,即当某个结点中样本数量小于这个值时自动将该结点标记为叶结点并计算输出概率,好处是可以尽量避免生长出太过于庞大的树,也就减少了过拟合的可能,也在一定程度上缩短了训练时间;
maxnodes:每颗基决策树允许产生的最大的叶结点数量,缺省时则每棵树无限制生长;
importance:逻辑型变量,控制是否计算每个变量的重要程度;
proxi:逻辑型变量,控制是否计算每颗基决策树的复杂度;
函数输出项:
call:训练好的随机森林模型的预设参数情况;
type:输出模型对应的问题类型,有'regression','classification','unsupervised';
importance:输出所有特征在模型中的贡献程度;
ntree:输出基决策树的颗数;
test$predicted:输出在ytest缺省,xtest给出的情况下,其对应的预测值;
test$confusion:输出在xtest,ytest均给出的条件下,xtest的预测值与ytest代表的正确标记之间的混淆矩阵;
test$votes:输出随机森林模型中每一棵树对xtest每一个样本的投票情况;
下面我们以鸢尾花数据为例,进行演示,具体过程如下:
> rm(list=ls()) > library(randomForest) > > #load data > data(iris) > > #split data > sam = sample(1:150,120) > train = iris[sam,] > test = iris[-sam,] > > #训练随机森林分类器 > rf = randomForest(Species~.,data=train, + classwt=table(train$Species)/dim(train)[1], + ntree=11, + xtest=test[,1:4], + importance=T, + proximity=T) > > #打印混淆矩阵 > rf$test$confusion NULL > > #打印正确率 > sum(diag(prop.table(table(test$Species,rf$test$predicted)))) [1] 1 > > #打印特征的重要性程度 > importance(rf,type=2) MeanDecreaseGini Sepal.Length 8.149513 Sepal.Width 1.485798 Petal.Length 38.623601 Petal.Width 31.085027 > > #可视化特征的重要性程度 > varImpPlot(rf)
特征重要程度可视化:

上图每个点表示将对应的特征移除后平均减少了正确率,所以点在图中位置越高就越重要;
输出每个样本接受基决策树投票的具体情况:
> #vote results of base decision tree > rf$test$votes setosa versicolor virginica 2 1.0000000 0.00000000 0.0000000 8 1.0000000 0.00000000 0.0000000 13 1.0000000 0.00000000 0.0000000 14 1.0000000 0.00000000 0.0000000 15 0.9090909 0.09090909 0.0000000 18 1.0000000 0.00000000 0.0000000 20 1.0000000 0.00000000 0.0000000 25 1.0000000 0.00000000 0.0000000 26 1.0000000 0.00000000 0.0000000 27 1.0000000 0.00000000 0.0000000 32 1.0000000 0.00000000 0.0000000 36 1.0000000 0.00000000 0.0000000 37 1.0000000 0.00000000 0.0000000 39 1.0000000 0.00000000 0.0000000 61 0.0000000 1.00000000 0.0000000 62 0.0000000 1.00000000 0.0000000 87 0.0000000 1.00000000 0.0000000 91 0.0000000 1.00000000 0.0000000 96 0.0000000 1.00000000 0.0000000 97 0.0000000 1.00000000 0.0000000 104 0.0000000 0.00000000 1.0000000 108 0.0000000 0.00000000 1.0000000 110 0.0000000 0.00000000 1.0000000 111 0.0000000 0.00000000 1.0000000 113 0.0000000 0.00000000 1.0000000 122 0.0000000 0.09090909 0.9090909 126 0.0000000 0.00000000 1.0000000 128 0.0000000 0.00000000 1.0000000 140 0.0000000 0.00000000 1.0000000 143 0.0000000 0.09090909 0.9090909 attr(,"class") [1] "matrix" "votes"
以上就是关于随机森林的基本内容,本篇今后会陆续补充更深层次的知识,如有笔误,望指出。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号