（数据科学学习手札23）决策树分类原理详解&Python与R实现

　　作为机器学习中可解释性非常好的一种算法，决策树(Decision Tree)是在已知各种情况发生概率的基础上，通过构成决策树来求取净现值的期望值大于等于零的概率，评价项目风险，判断其可行性的决策分析方法，是直观运用概率分析的一种图解法。由于这种决策分支画成图形很像一棵树的枝干，故称决策树。在机器学习中，决策树是一个预测模型，他代表的是对象属性与对象值之间的一种映射关系。

 

一、初识决策树

　　决策树是一种树形结构，一般的，一棵决策树包含一个根结点，若干个内部结点和若干个叶结点：

叶结点：树的一个方向的最末端，表示结果的输出；

根结点：初始样本全体；

内部结点：每个内部结点对应一个属性测试（即一次决策）

从根结点——每个叶结点，形成各条判定序列；我们的进行决策树分类器训练的学习目的是产生一棵泛化能力强，即处理未见示例能力强的决策树，其基本流程遵循“分而治之”的策略：

算法过程：

　　Step1：输入样本集D{(x₁,y₁),(x₂,y₂),...,(x_n,y_n)}，属性集A{a₁,a₂,...,a_d}，全体样本集储存在根结点中；

　　Step2：从属性集A中经过一定的规则（具体规则由算法决定）挑选出一个最佳属性a₁,所有样本从根结点流向该决策结点，根据样本在a₁这个属性上的取值，流向对应的方向（如下图）：

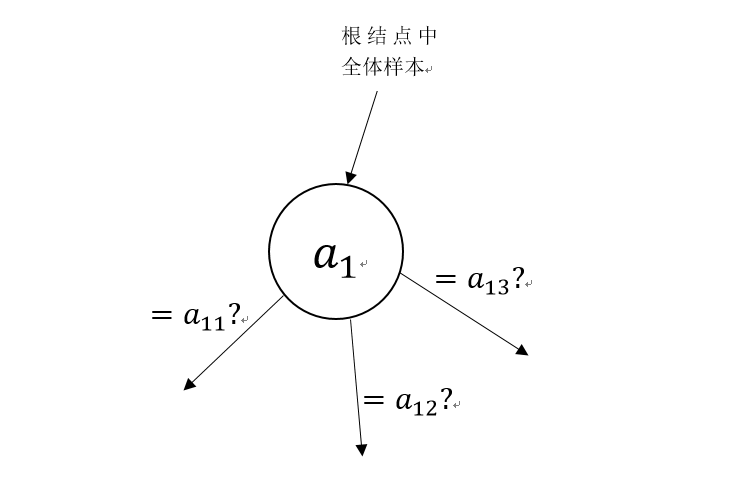
在样本集通过某个属性判断，确定不同的流向后，会有以下几种情况:

　　　　1.流向某个方向的所有样本只存在一个类别y₀，这时把这个方向标记为叶结点，即最终从这个方向流出的样本都可直接判定为类别y₀；

　　　　2.通过当前属性判断后，某个方向没有样本流出，这通常是样本量不够多导致的样本多样性不足，这时可以将这方向标记为叶结点，将训练集中各类别的比例作为先验概率，将所有从这个方向流出的新样本都标记为先验概率最大的那个类别；

　　　　3.在某个属性判断上，所有训练样本都取同一个值，和情况2相似，也是在其他可能方向上无训练样本流出，在对新样本处理时方法同2；

　　Step3：通过Step2的过程将所有属性利用完之后，形成了一棵完整的树，其每个判断路径上都经过了所有属性，这时对所有的叶结点规定输出类别为训练过程中到达该叶结点中的样本中比例最大（即利用了先验分布）的那一类，至此，一棵决策树训练完成。

 

二、训练过程属性的选择

现在我们知道了决策树的训练过程，但对于哪一个属性放在第一位，哪个放在第二位以此类推，还依然不知晓，这就是决策树中非常重要也非常巧妙的一点——划分选择；

划分选择：决策树学习的关键是如何选择最优划分属性，我们希望随着划分过程不断进行，决策树的分支结点所包含的样本尽可能属于同一类别，即结点的纯度（purity）越来越高，下面我们介绍几种不同的衡量样本纯度的规则，他们也分别产生了不同的决策树算法：

1.信息增益

在定义信息增益之前，我们先介绍以下概念：

信息熵（information entropy）：

度量样本集合纯度最常用的一种指标，假定当前样本集合D中第k类样本所占的比例为p_k(k=1,2,...,|y|)，则D的信息熵定义为：

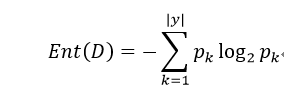
Ent(D)越小，D的纯度越高，其中|y|表示属性的可能取值数，假定对离散属性a有V个可能的取值{a¹,a²,...,a^V}，使用a来对样本集D进行划分，产生V个分支结点，其中第v个分枝结点流入D中所有在属性a取值为a^V的样本，记作D^V，则属性a对D进行划分所获得的信息增益为：

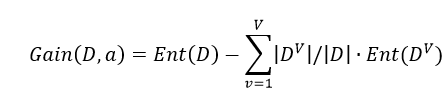
其中|D^V|指D中在a属性取a^V的样本数量，则|D^V| / |D|可看作在a^V方向上的权重；

*原则：信息增益越大，意味着使用a属性进行划分所划得的“纯度提升”最大，即当前最优划分为：

 

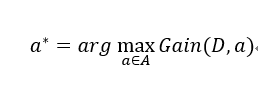
2.增益率

有些时候，若样本集中含有“编号”这种使得分支结点纯度远大于其他有效属性的非有效属性（因为编号会将每一个样本独立分开），导致各个编号的分支能变成叶结点（对应特殊情况中的1），这样的决策树显然不具有泛化能力，无法对新样本进行预测，即，这种情况下信息增益准则对可取值数目较多的属性有所偏好，为减少这种偏好可能带来的不利影响，下面引入：

C4.5算法：

不直接使用信息增益，而是使用“增益率”来选择当前最优划分属性；

增益率定义为：

其中，

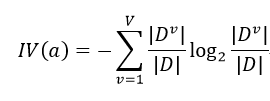
叫做属性a的固有值，属性a的可能取值数目越大（即V越大），则IV(a)的值通常会越大；与信息增益相比，增益率对属性取值数目较少的属性有偏好，因此C4.5算法并不直接以所有属性的增益率作为比较依据，而是有一个启发式的过程：先选择候选划分属性中信息增益高于平均水平的属性，再从中选择增益率最高的。

 

3.基尼系数

CART决策树（Classfication and Regression Tree）使用基尼指数来选择划分属性，则数据D的纯度可用基尼值来度量：

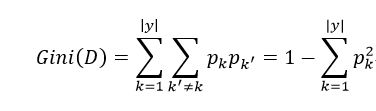
Gini(D)反映了从数据集D中抽取两个样本，其类别标记不一致的概率，即Gini(D)越小，数据集D的纯度越高，则对一个属性a，其基尼指数为：

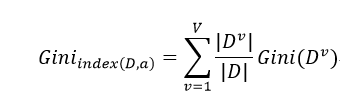
所以在候选属性集合A中，选择当前剩余属性中使得划分后基尼指数最小的作为当前最优划分属性，即：

 

 三、剪枝处理

 　　在决策树学习中，为了尽可能正确分类训练样本，结点划分过程不断重复，有时会造成决策树分支过多，这时就可能因训练集过度学习，以致于把训练集本身的一些特点当作所有数据都具有的一般性质，从而导致过拟合。

　　通过主动去掉一些分支来降低过拟合的风险的过程就叫做剪枝。

决策树剪枝的基本策略：

　　1.预剪枝（prepruning）

在决策树生成过程中，对每个结点在划分前先进行性能估计，若当前结点的划分不能带来决策树泛化性能的提升，则停止划分并将当前结点标记为叶结点；

　　2.后剪枝（post-pruning）

先从训练集生成一棵完整的决策树，然后自底向上地对非叶结点进行考察，若将该结点对应的子树替换成叶结点能带来决策树泛化能力提升，则将该子树替换成叶结点。

预剪枝：

　　步骤：

　　Step1：为衡量泛化能力，利用留出法，划分样本集为训练集和验证集；

　　Step2：根据信息增益准则，选出a^*作为根结点下第一个非叶结点，分别训练通过这一属性进行分类的模型，和将该结点作为叶结点的模型，比较这两个模型在验证集上的正确率，选择更优的方案；

　　Step3：重复Step2对所有属性进行考察，直到最终决策树完成；

*仅有一层划分的决策树称为“决策树桩”（decision stump）

　　原则：剪去（淘汰）正确率小于或等于当前正确率（即当前最高正确率）的分支操作；

　　优点：预剪枝使得决策树的很多分支没有展开，降低了模型过拟合的风险，还显著减少了决策树的训练时间开销和测试时间开销；

　　缺点：有些分支的当前划分虽不能提升泛化能力，甚至可能导致泛化能力暂时下降，但在其基础上进行的后续划分却有可能导致性能显著提升；

　　　　　预剪枝基于“贪心”本质禁止这些分支展开，只关心当前性能表现，给预剪枝决策树模型带来了欠拟合的风险。

 

后剪枝： 

　　步骤：

　　Step1：对于不经任何剪枝处理，仅依据某个信息纯度评价方法最终形成的一棵完整的使用了所有属性的决策树，从其最靠后的非叶结点开始，分别训练不剪去该结点和剪去该结点时的模型，比较泛化能力；

　　Step2：若泛化能力得到了提高，则采取相应的模型变更/维持原状操作；

　　Step3：重复上述过程直到所有非叶结点完成剪枝效果评估。

　　原则：若剪枝后正确率得到提高，则采取剪枝操作，否则不变；

　　优点：欠拟合风险很小，泛化能力往往优于预剪枝决策树；

　　缺点：后剪枝过程是在生成完全决策树之后进行的，并且需自底向上对树中所有非叶结点进行逐一考察后，因此训练时间开销巨大。

 

以上就是决策树算法的一些基本常识，下面我们分别在Python和R中实现决策树算法：

 

四、Python

　　我们利用sklearn模块中的tree下属的DecisionTreeClassifier()进行决策树分类，关于其细节在sklearn的官网中有详细介绍：http://scikit-learn.org/stable/modules/generated/sklearn.tree.DecisionTreeClassifier.html#sklearn.tree.DecisionTreeClassifier，下面我们对其主要参数进行介绍：

criterion : 字符型，用来确定划分选择依据的算法，有对应CART树算法的“gini”和对应ID3算法的“entropy”，默认为“gini”

splitter : 字符型，用来确定选择每个属性判断结点的方式，依据的是criterion中确定的指标数值，有对应最佳结点的“best”和对应随机选择的“random”，默认是“best”

max_depth :整型，用来确定决策树的最大深度（即最多的非叶结点数目规模），默认为None，即不限制深度

min_samples_split :有两种情况，

　　1.整型，这时该参数确定用于分割非叶结点的最小样本数，即如果小于该预设值，则该结点因为信息不足可以直接根据先验分布生成为叶结点输出结果，默认值2；

　　2.浮点型，这时该参数功能不变，只是确定的min_samples_split变为min_samples_split*n_samples，这里代表百分比。

min_samples_leaf :有两种情况，

　　1.整型，这时该参数确定用于生成叶结点的最小样本数，即小于该数值时不可生成叶结点，默认值为1；

　　2.浮点型，同min_samples_split

min_weight_fraction_leaf :浮点型，该参数用于确定每个样品的权重，在最终在叶结点产生结果时起作用，主要用于类别不平衡时的再缩放操作，默认每个样品权重相等；

max_features : 该参数用于确定每一次非叶结点属性划分时使用到的属性数目（在信息增益和基尼指数的计算中起作用），默认使用全部属性，有以下几种情况：

　　1.整型，这时传入的整数即为每次分割时考虑的最大属性数；

　　2.浮点型，这时最大属性数是该浮点参数*属性总数；

　　3.字符型，“auto”时，最大属性数为属性总数开根号；“sqrt”时，同“auto”；“log2”时，最大属性数为属性总数取对数；

　　4.None，这时最大属性数即为属性总数；

 max_leaf_nodes : 该参数用于确定最终的决策树模型的最大叶结点数量，默认为无限制，即None

 class_weight :用于处理类别不平衡问题的权重，建议使用“balanced”，即自动根据先验分布赋权，默认为None，即忽略权重，每一类同等看待

以上就是sklearn.tree.DecisionTreeClassifier的主要参数介绍，下面我们以kaggle playground中的泰坦尼克号遇难者数据作为演示数据对生还与否进行二分类：

数据说明：

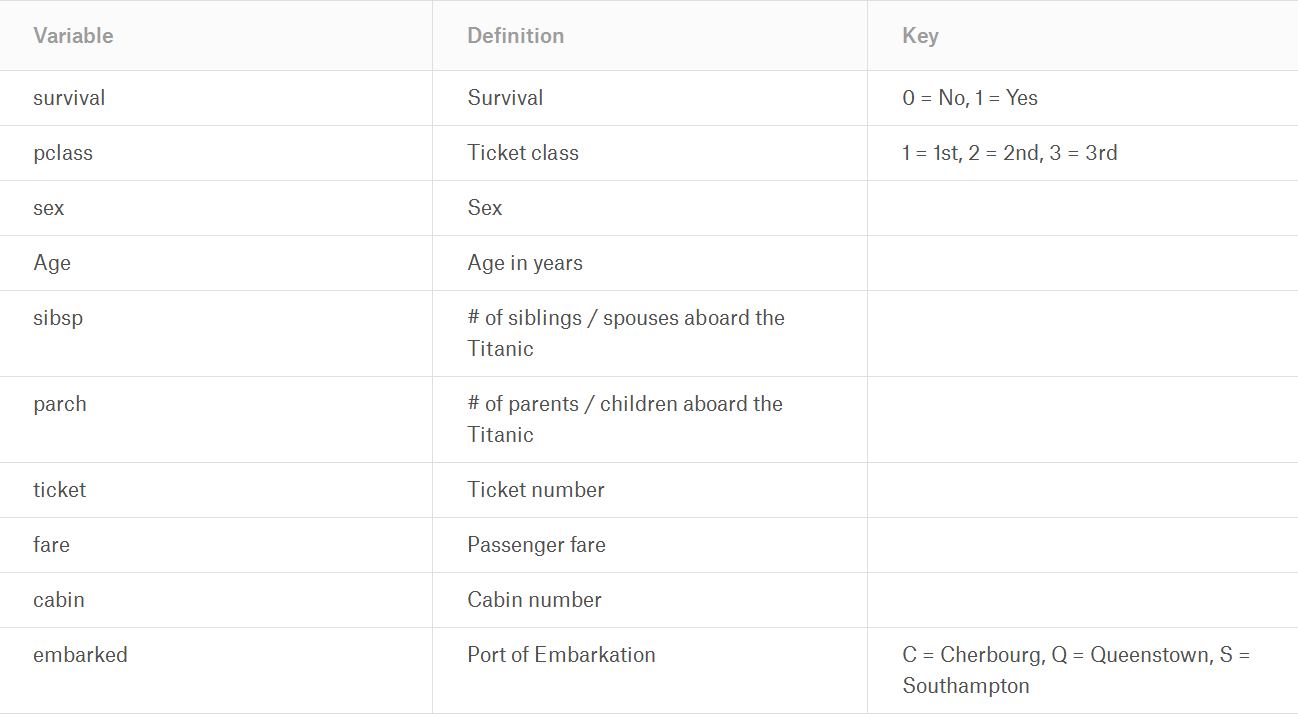
 代码：

 

from sklearn.tree import DecisionTreeClassifier
from sklearn.model_selection import train_test_split
import pandas as pd
import numpy as np


'''读入数据'''
raw_train_data = pd.read_csv('train.csv')

train = raw_train_data.dropna()

target_train = train['Survived'].tolist()

#Ticket class
pclass = train['Pclass'].tolist()
sex = train['Sex'].tolist()

Sex = []
for i in range(len(sex)):
    if sex[i] == 'male':
        Sex.append(1)
    else:
        Sex.append(0)
age = train['Age'].tolist()

#在船上兄弟姐妹的数量
SibSp = train['SibSp'].tolist()

#在船上父母或孩子的数量
Parch = train['Parch'].tolist()

Fare = train['Fare'].tolist()

#登船的港口
Embarked = train['Embarked'].tolist()
sabor_C = []
sabor_Q = []

#为登船港口设置哑变量
for i in range(len(Embarked)):
    if Embarked[i] == 'C':
        sabor_C.append(1)
        sabor_Q.append(0)
    elif Embarked[i] == 'Q':
        sabor_Q.append(1)
        sabor_C.append(0)
    else:
        sabor_Q.append(0)
        sabor_C.append(0)

'''定义自变量与目标'''
train_ = np.array([Sex,age,sabor_C,sabor_Q]).T
target_ = np.array(target_train)

'''重复多次随机分割样本集的训练取正确率平均值'''
S = []
for i in range(1000):
    X_train, X_test, y_train, y_test = train_test_split(train_, target_, test_size=0.3)
    clf = DecisionTreeClassifier(class_weight='balanced',max_depth=2)
    clf = clf.fit(X_train,y_train)
    S.append(clf.score(X_test,y_test))

'''打印结果'''
print('平均正确率：'+str(np.mean(S)))

 

训练效果：

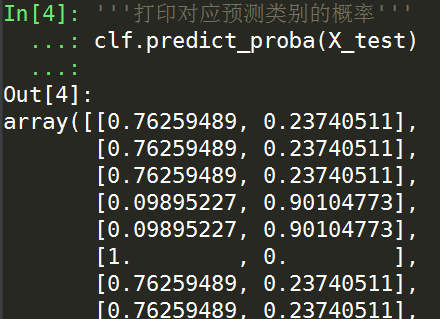
 利用训练好的模型不仅可以输出新样本值类别的预测值，还可以输出对应的概率，这个概率即是叶结点的先验分布：

'''打印对应预测类别的概率'''
clf.predict_proba(X_test)

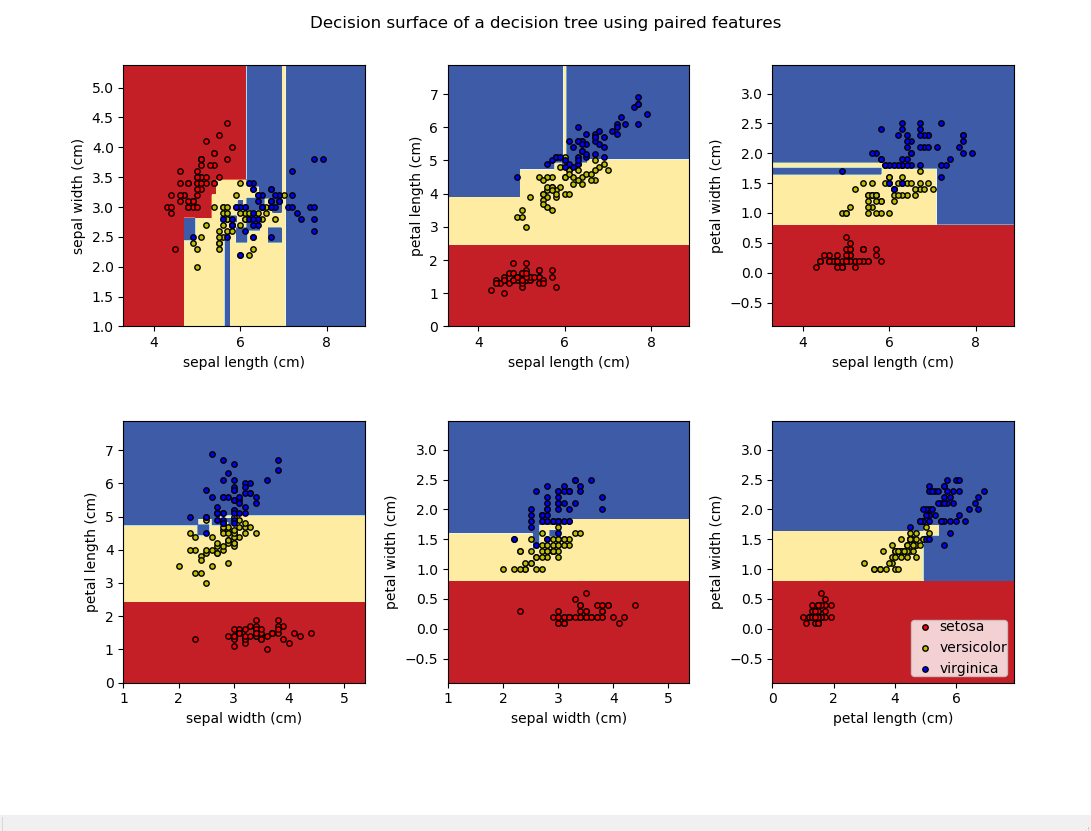
 我们都知道决策树是利用与各坐标轴平行的线段拼凑而成组成决策边界来划分样本点，在自变量个数不多时我们可以绘制出决策边界的示意图来加强可解释性，下面以鸢尾花数据为例：

print(__doc__)

import numpy as np
import matplotlib.pyplot as plt

from sklearn.datasets import load_iris
from sklearn.tree import DecisionTreeClassifier

# Parameters
n_classes = 3
plot_colors = "ryb"
plot_step = 0.02

# Load data
iris = load_iris()

for pairidx, pair in enumerate([[0, 1], [0, 2], [0, 3],
                                [1, 2], [1, 3], [2, 3]]):
    # 对变量中所有两两变量间进行匹配
    X = iris.data[:, pair]
    y = iris.target

    # Train
    clf = DecisionTreeClassifier().fit(X, y)

    # 绘制决策边界
    plt.subplot(2, 3, pairidx + 1)

    x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
    y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
    xx, yy = np.meshgrid(np.arange(x_min, x_max, plot_step),
                         np.arange(y_min, y_max, plot_step))
    plt.tight_layout(h_pad=0.5, w_pad=0.5, pad=2.5)

    Z = clf.predict(np.c_[xx.ravel(), yy.ravel()])
    Z = Z.reshape(xx.shape)
    cs = plt.contourf(xx, yy, Z, cmap=plt.cm.RdYlBu)

    plt.xlabel(iris.feature_names[pair[0]])
    plt.ylabel(iris.feature_names[pair[1]])

    # 绘制训练样本点
    for i, color in zip(range(n_classes), plot_colors):
        idx = np.where(y == i)
        plt.scatter(X[idx, 0], X[idx, 1], c=color, label=iris.target_names[i],
                    cmap=plt.cm.RdYlBu, edgecolor='black', s=15)

plt.suptitle("Decision surface of a decision tree using paired features")
plt.legend(loc='lower right', borderpad=0, handletextpad=0)
plt.axis("tight")
plt.show()

 

 

五、R

在R中使用决策树相关算法有一个很大的方便之处，就是在对决策树可视化的时候，我们都知道决策树是一种解释性很强的机器学习算法，这是它被广泛使用的一个原因之一，在R中绘制决策树非常方便；在R中，一棵决策树的初步生成与剪枝是使用两个不同的函数进行操作的，我们这里使用rpart包来创建分类树，其中rpart()函数创建决策树，prune()函数用来进行树的剪枝，具体参数如下：

对rpart():

formula：这是R中很多算法的输入格式，用~连接左端的target列名称和右端的自变量列名称；

data：输入数据框的名称；

weights：可选的自定义类别权重，主要在类别不平衡时使用，类似逻辑分类中的再缩放；

na.action：对缺失值进行处理，默认删去target列缺失的样本，但保留自变量存在缺失的样本（决策树中对缺失值较为宽容，有对应的处理方法）

parms：默认为“gini”指数，即CART决策树分割结点的方法；

control：这是一个非常重要的参数集合，与Python在主体函数中赋参不同，rpart中关于决策树的调参都集合在这个control参数中，control的赋值格式为control=rpart.control()，对于rpart.control可以调节的参数如下：

　　minspilt：整数，默认为20，表示对节点中样本进行划分的最小样本数，小于这个数目则直接根据先验分布生成叶结点；

　　minbucket：整数，默认值为round(minspilt/3)，表示一个阈值，若当前结点样本数小于这个阈值，则生成叶结点；

　　cp：复杂度，默认0.01；

　　maxcompete：在每次节点划分中选择使用的变量个数，默认为4，用于计算信息增益指标；

　　xval：交叉验证的数量，默认10，即十折交叉验证；

　　maxdepth：控制决策树的最大深度，这个最大深度指的是所有叶结点中距离根结点最远的距值，所以决策树桩深度为0；

 对prune():

tree：指定先前保存生成好的决策树的变量名；

cp：复杂度，默认0.1，用于决定对决策树裁剪的程度；

下面我们以Fisher的鸢尾花数据进行决策树分类演示：

> rm(list=ls())
> library(rpart.plot)
> library(rpart)
> #挂载数据
> data(iris)
> data <- iris
> #留出法抽出0.8的训练集与0.2的测试集
> sam <- sample(1:150,120)
> train_data <- data[sam,]
> test_data <- data[-sam,]
> #训练决策树
> dtree <- rpart(Species~.,data=train_data)
> #绘制决策树复杂度变化情况
> plotcp(dtree)
> #进行剪枝，这里设置复杂度阈值为0.01
> dtree.pruned <- prune(dtree, cp=0.01)
> #绘制剪枝后的决策树模型结构
> prp(dtree.pruned,type=0)
> title('Decision Tree for Iris Data')
> #对验证集代入训练好的模型进行预测
> dtree.pred <- predict(dtree.pruned,test_data[,1:4],type='class')
> #打印混淆矩阵
> (dtree.perf <- table(test_data[,5],dtree.pred))
            dtree.pred
             setosa versicolor virginica
  setosa         10          0         0
  versicolor      0         10         2
  virginica       0          0         8

决策树结构：

 

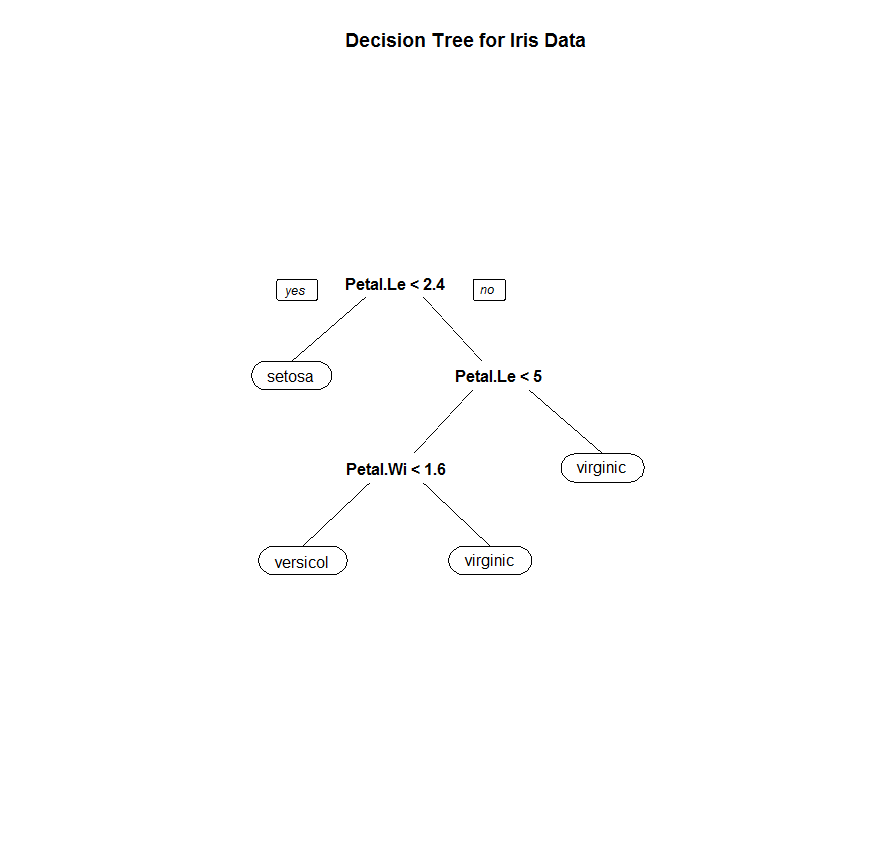
 可以看出，决策树在该数据集上的预测效果非常不错，且只使用了有效的数据，节省了计算时间成本。

 

六、关于决策树实践中的建议

本节内容选自sklearn官网决策树页面：http://scikit-learn.org/stable/modules/tree.html#tree-classification，由笔者自行摘抄翻译：

　　1.决策树在应对高维数据时很容易过拟合，因此保持自变量个数和样本个数间的比例非常重要，其实不管是对什么预测算法，当样本个数接近自变量个数时都容易发生过拟合；

　　2.可以考虑对自变量进行维数约简，或进行特征选择，以最大程度保留较少更有说服力的自变量，以尽量减少过拟合的风险；

　　3.多使用决策树结构的可视化方法，可以帮助你理解你当前树的生长效果，也可以更好的与现实业务联系起来进行解释；

　　4.树的深度（即距离最远的叶结点对应距离根结点的距离）初始化设置为3较好，再逐步增长该参数，观察训练效果的变化情况，以作出最好的选择，以及控制过拟合情况；

　　5.使用min_samples_spilt或与其等价的参数来控制生成叶结点时的样本个数下限，因为通常该参数越小，树过拟合的风险都越大，因此尽早生成叶结点可以缓解对样本数据独特性的放大，进而减少过拟合风险；

　　6.在训练之前尽量平衡类别间的比例，以避免训练结果因为类别的严重不平衡而产生虚假结果（比如样本中9个正例1个反例，训练出的模型全部归类为正例也能取得90%的正确率，但这不可靠），或者调节sample_weight来对所有类别进行再缩放；

 

以上就是决策树的基本知识，若有笔误，请指出。