(数据科学学习手札20)主成分分析原理推导&Python自编函数实现
主成分分析(principal component analysis,简称PCA)是一种经典且简单的机器学习算法,其主要目的是用较少的变量去解释原来资料中的大部分变异,期望能将现有的众多相关性很高的变量转化为彼此互相独立的变量,并从中选取少于原始变量数目且能解释大部分资料变异情况的若干新变量,达到降维的目的,下面我们先对PCA算法的思想和原理进行推导:
主成分即为我们通过原始变量的线性组合得到的新变量,这里假设xi(i=1,2,...,p)为原始变量,yi(i=1,2,...,p)为主成分,他们之间的关系如下:
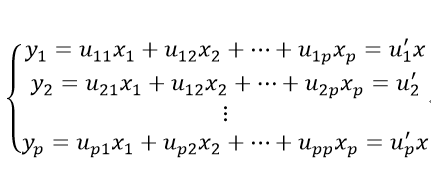
其中,uij为第i个主成分yi与第j个原始变量xj间的线性相关系数,y1,y2,... ... ,yp分别为第一、二...、p主成分,且u11,... ... ,u1p通过与对应的原始变量进行线性组合,使得y1得到最大解释变异的能力,接着u21,... ... ,u2p通过与对应的原始变量进行线性组合,使得y2对原始变量中的未被y1解释的变异部分获得最大的解释能力,依次类推,直到p个主成分均求出;通常我们基于对原始变量降维的目的,会从这p个主成分中选取少于p的m个成分,且希望m越小的同时,总的解释能力能超过80%,值得注意的是,得到的这些主成分彼此之间线性无关;
设y=a1x1+a2x2+...+apxp=a'x,其中a=(a1,a2,...,ap)',x=(x1,x2,...,xp)',求主成分就是寻找x的线性函数a'x,使得相应的方差达到最大,即var(a'x)=a'∑a,且a'a=1(使a唯一),∑为x的协方差矩阵;
推导:
基于实对称矩阵的性质(每个实对称矩阵都可以分解为单位实特征向量和实特征值),譬如对任意实对称矩阵A,有
A=QΤQ'
其中,Q为列向量由A的特征向量组成的矩阵,T为对角线元素为A的特征值降序排列的对角矩阵,注意这里的特征值与Q中特征列向量一一对应;而针对这个性质,回到PCA中,因为x的协方差矩阵∑为实对称矩阵,设∑的特征根为λ1≥λ2≥...≥λp,相对应的单位特征向量为u1,u2,...,up,令U=(u1,u2,...,up),则U'U=UU'=I,即U为正交阵,且:
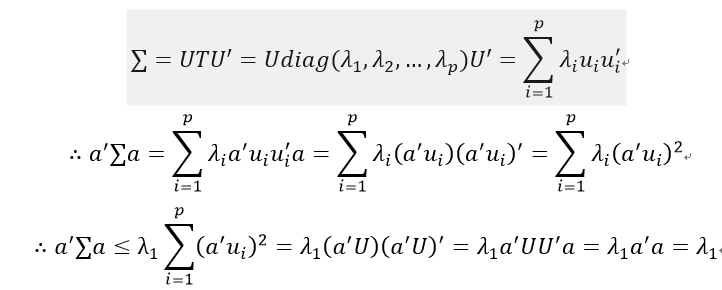
当取a=u1时:
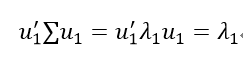
所以y1=u'1x就是第一主成分,它的方差为:
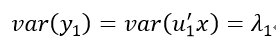
同理:
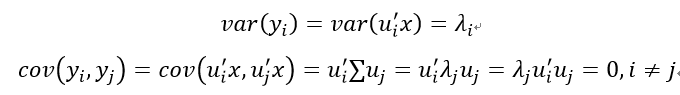
通过上述推导,我们可以使用原始变量的协方差矩阵来求解各主成分,在计算出所有主成分之后,就要进行主成分的选择,由于主成分与原始变量的协方差矩阵直接挂钩,我们定义第k个主成分yk的方差贡献率:
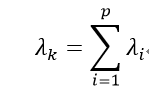
则主成分的选择过程即为从贡献率最大的主成分算起,一直到累计贡献率满足要求为止;
再定义主成分负荷(loadings,在因子分析中称为因子载荷):
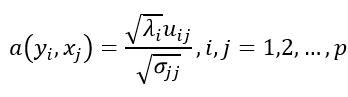
即为第i个主成分与第j原始变量的相关系数,矩阵A=(aij)称为因子载荷矩阵,在实际中常用aij代替uij作为主成分系数,因为它是标准化系数,能反映变量影响的大小;
到此我们已经知道了主成分分析的主要原理,接下来我们分别在Python中自编函数来实现这个过程:
Python
使用numpy和sklearn包搭建自定义的PCA算法(除标准化和求解特征值、特征向量外其余功能均由自定义函数实现)
import numpy as np import pandas as pd from sklearn import preprocessing '''读入数据''' original_data = pd.read_csv(r'C:\Users\windows\Desktop\kaggle\A\wine_red.csv',encoding='ANSI') '''数据预处理''' data = np.asmatrix(original_data.iloc[:,4:]) class My_PCA(): def __init__(self): print('自编PCA算法') '''根据输入的数据集和指定的累计贡献率阈值''' def PCA(self,data,alpha=0.8): '''数据标准化''' scaler = preprocessing.StandardScaler().fit(data) input = scaler.transform(data).astype(dtype='float32') '''计算相关系数矩阵''' cor = np.corrcoef(input) '''计算相关系数矩阵的特征值与对应的特征向量''' eigvalue = np.linalg.eig(cor)[0].astype(dtype='float32') eigvector = np.linalg.eig(cor)[1].astype(dtype='float32') '''计算各主成分方差贡献''' contribute = [eigvalue[i] / np.sum(eigvalue) for i in range(len(eigvalue))] '''保存特征值排序后与之前对应的位置''' sort = np.argsort(contribute) '''根据传入的累计贡献率阈值alpha提取所需的主成分''' pca = [] token = 0 i = 1 while (token <= alpha): token = token + contribute[sort[len(input) - i]] pca.append(sort[len(input) - i]) i += 1 '''将得到的各主成分对应的特征值和特征向量保存下来并作为返回值''' PCA_eig = {} for i in range(len(pca)): PCA_eig['第{}主成分'.format(str(i+1))] = [eigvalue[pca[i]], eigvector[pca[i]]] return PCA_eig '''将算法所在的类赋值给自定义变量''' test = My_PCA() '''调用类中的PCA算法来产出所需的主成分对应的特征值和特征向量''' pca = test.PCA(data) '''显示最大的主成分对应的特征值和特征向量''' pca['第1主成分']
查看第1主成分结果如下:
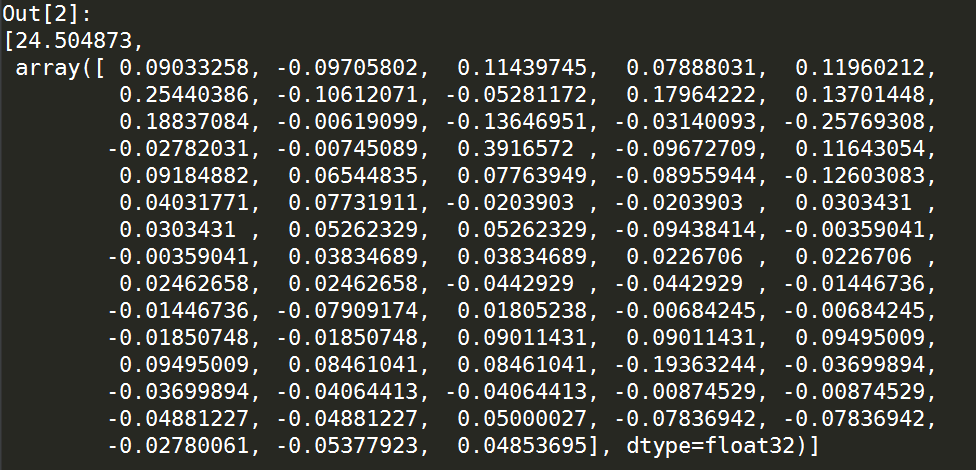
以上就是关于PCA算法的原理及自编函数实现,下一篇中我们将仔细介绍Python和R中各自成熟的第三方PCA函数,敬请期待。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号