数据的表示和运算
数值与编码
进位计数制及其相互转换
在计算机系统内部, 所有的信息都是用二进制进行编码的, 这样做的原因有以下几点
1. 二进制只有两种状态, 使用有两个稳定状态的物理器件就可以表示二进制的每一位, 制造成本比较低。
2. 二进制位1和0正好与逻辑值"真"和"假"对应, 为计算机实现逻辑运算和程序中的逻辑判断提供了便利的条件
3. 二进制的编码和运算规则都比较简单, 通过逻辑门电路能方便地实现算术运算
r进制计数法
进位计数法是一种计数方法, 常用的进位计数法有十进制、二进制、八进制、十六进制等。在进位计数法中, 每个数位所用到的不同数码的个数称为基数。十进制的基数为10(0~9),每个数位记满10就向高位进位, 即"逢十进一"
一个r进制数\(K_{n}K_{n-1}...K_{0}K_{-1}...K_{-m}\)的数值可表示为\(K_{n}r^n+K_{n-1}r^{n-1}+...+K_{-1}r^{-1}+...+K_{-m}r^{-m}=\sum_{i=n}^{{-m}}K_{i}r^i\)
基数: 每个数码位所用到的不同符号的个数, r进制的基数为r
二进制: 0, 1 八进制: 0, 1, 2, 3, 4, 5, 6, 7 十进制: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 十六进制: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F
二进制转换为八进制和十六进制
对于一个二进制混合数(即包含整数部分, 又包含小数部分), 在转换时应以小数点为界。其整数部分, 从小数点开始往左数, 将一串二进制数分为3位(八进制)一组或4位(十六进制一组), 在数的最左边可根据需要加"0补齐"; 对于小数部分, 从小数点开始往右数, 也将一串二进制数分为3位一组或4位一组, 在数的最右边可根据需要加"0"补齐。最终使总的位数为3或4的整数倍, 然后分别用对应的八进制数或十六进制数取代
二进制 --> 八进制 3位一组, 每组转换成对应的八进制符号 001 111 000 101 . 011 010 1 7 0 2 . 3 2 八进制 二进制 -> 十六进制 4位一组, 每组转换成对应的十六进制符号 0011 1100 0010 . 0110 1000 3 C 2 . 6 8 十六进制
同样, 由八进制数或十六进制数转换成二进制数, 只需要将每位改为3位或4位二进制数即可(必要时同时去掉整数最高位或小数最低位的0)。八进制和十六进制之间的转换也能方便实现, 十六进制数转八进制数(或八进制数转十六进制数)时, 先将十六进制(八进制)数转为二进制数, 然后由二进制数转换为八进制(十六进制)数较为方便
八进制 --> 二进制 每位八进制对应的3位二进制 (251.5)8 --> (010 101 001. 101)2 十六进制 -> 二进制 每位十六进制对应的4位二进制 (AE86.1)16 --> (1010 1110 0110. 0001)2
各种进制的常见书写方式
二进制(Binary) -- (1010001010010)2 1010001010010B 八进制 -- (1652)8 十六进制(Hexadecimal) -- (1652)16 1652H 0x1652 十进制(Decimalism) -- (1652)10 1652D
十进制数转换为任意进制数
一个十进制数转换为任意进制数, 常采用基数乘除法。这种转换方法对十进制数的整数部分和小数部分将分别进行处理, 对整数部分用除基取余法, 对小数部分用乘基取整法, 最后将整数部分与小数部分的转换结果拼接起来。
除基取余法(整数部分的转换): 整数部分除基取余, 最先取得的余数为数的最低位, 最后取得的余数为数的最高位, 商为0时结束
乘基取整法(小数部分的转换): 小数部分乘基取整, 最先取得的整数为数的最高位, 最后取得的整数为数的最高位, 乘积为1.0(或满足精度要求)时结束
十进制 --> 二进制 (123.6875)10 --> (1111011.1011)2
真值和机器数
在日常生活中, 通常用正号、负号来分别表示正数(正号可省略)和负数, 如+15, -8等。这种带"+", "-"符号的数称为真值。真值是机器数所代表的实际值
在计算机中, 通常采用的符号和数值一起编码的方式来表示数据, 通常用"0"表示"正", 用"1"表示"负"。如0101表示+5, 这种把符号"数字化"的数称为机器数
BCD码
二进制编码的十进制数(Binary-Coded Decimal, BCD)通常采用4位二进制来表示一位十进制数中的0~9这10个数码。这种编码方法使二进制数和十进制数之间的转换得以快速进行。但4位二进制可以组合出16种代码, 因此必有6种状态为冗余状态
1) 8421码, 它是一种有权码, 设其各位的数值为b3, b2, b1, b0, 则权值从高到低依次为8, 4, 2, 1, 它表示的十进制数为D=8b3 + 4b2 + 2b1 + 1b3。如8-->1000; 9-->1001, 若两个8421码相加之和小于等于(1001)2即(9)10, 则不需要修正; 若相加之和大于等于(1010)2即(10)10, 则要加6修正(从1010到1111这6个为无效码, 当运算结果落于这个区间时, 需要将运算结果加上6), 并向高位借位
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 0000 | 0001 | 0010 | 0011 | 0100 | 0101 | 0110 | 0111 | 1000 | 1001 |
2) 余3码, 这是一种无权码, 是在8421码的基础上加(0011)2形成的, 因此每个数都多余"3"。 如8-->1011; 9-->1100
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 0011 | 0100 | 0101 | 0110 | 0111 | 1000 | 1001 | 1010 | 1011 | 1100 |
3) 2421码, 也是一种有权码, 权值由高到低分别为2, 4, 2, 1, 特点是大于等于5的4位二进制数中最高位为1, 小于等于5的最高位为0, 如5->1011, 而非0101
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 0000 | 0001 | 0010 | 0011 | 0100 | 1011 | 1100 | 1101 | 1110 | 1111 |
字符与字符串
由于计算机内部只能识别和处理二进制代码, 所以字符都必须按照一定的规则用一组二进制编码来表示
1. ASCII码
国际上普遍采用的一种字符系统是7位二进制编码的ASCII码, 它可表示10个十进制数码、52个英文大写字母和小写字母(A~Z、a~z)及一定数量的专用符号(如$、%、+、=等)、共128个字符
在ASCII码中, 编码值0~31为控制字符, 用于通信控制或设备的功能控制; 编码值127是DEL码, 编码值32是空格SP; 编码值32~126共95个字符可称为可印刷字符。
2. 汉字的表示和编码
国家标准GB2312-80中, 每个编码用两字节表示, 收录了汉字和各种符号共7445个。区位码是国家标准局1981年颁布的标准, 它用两个字节表示一个汉字, 每字节用7位码, 并将汉字和图形符号排列在一个94行94列的二维代码表中。区位码是4位十进制数, 前2位是区码, 后2位是位码, 所以称为区位码
国标码将十进制的区位码转换为十六进制后, 再在每个字节上加上20H。国标码两字节的最高位都是0, ASCII码的最高位也是0, 为了方便计算机区分中文字符和英文字符, 将国标码两个字节的最高位都改为"1", 这就是汉字内码。
区位码和国标码都是输入码, 他们和汉字内码的关系(十六进制): 国标码 = (区位码)16 + 2020H 汉字内码 = (国标码)16 + 8080H
仅有英文的字符串在计算机中的表示
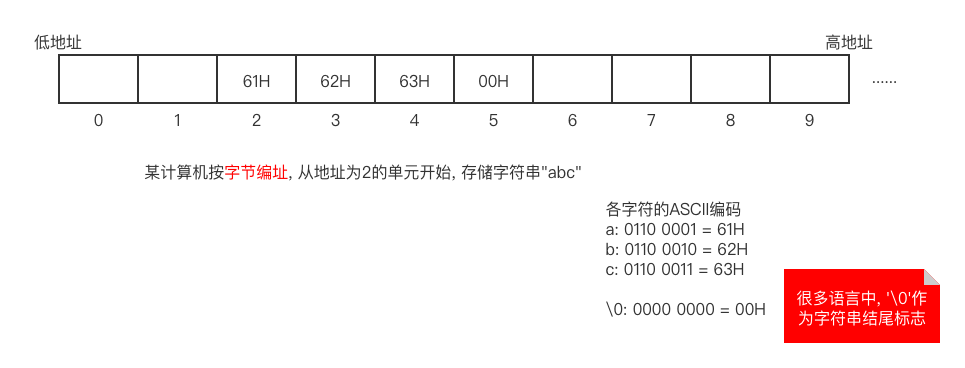
带有中文的字符串再计算机中的表示

校验码
校验码是指能够发现或能够自动纠正错误的数据编码, 也称为检错纠错编码。校验码的原理是通过增加一些冗余码, 来校验或纠错编码。
由若干位代码组成的一个字叫做码字。将两个码字逐步进行对比, 具有不同的位的个数称为两个码字之间的距离。一种编码方案可能有若干个合法码字, 各合法码字间的最小距离称为"码距"d。
当d=1时, 无检错能力; 当d=2时, 有检错能力; 当d>=3时, 若涉及合理, 可能具有检错、纠错能力
1 奇偶校验码
奇校验码: 整个校验码(有效信息位和校验位)中"1"的个数为奇数
偶校验码: 整个校验码(有效信息位和校验位)中"1"的个数为偶数
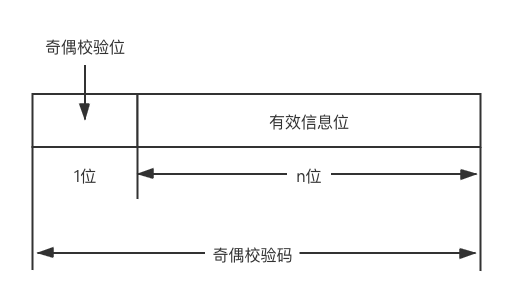
例: 给出两个编码1001101和1010111的奇校验码和偶校验码 设最高位为校验位, 余7位是信息位, 则对应的奇偶校验码为: 奇校验码: 11001101 01010111 偶校验码: 01001101 11010111 偶校验的硬件实现: 各信息进行异或(模2加运算), 得到的结果即为偶校验位 求偶校验位: 1 0 0 1 1 0 1 = 0 1 0 1 0 1 1 1 = 1 进行偶校验(所有位进行异或, 若结果为为1说明出错) 0 1 0 0 1 1 0 1 = 0 1 1 0 1 0 1 1 0 = 1
2 海明校验码
海明码是广泛采用的一种有效的校验码, 它实际上是一种多重奇偶校验码。其实现原理是在有效信息中加入几个校验位形成海明码, 并把海明码的每个二进制为分配到几个奇偶校验组中。当某一位出错后, 就会引起有关的几个校验位的值发生变化, 这不但可以发现错位, 还能指出错位的位置, 为自动纠错提供依据。
假设信息位为n, 校验位为k, 那么则共有\(2^k\)种状态, 且信息位+校验位共n+k位, 那么可以得出\(2^k \geqslant n + k + 1\), 因为n+k位中任何一位都可能出错, 并且还需要包含一种正确的方式
例如: 信息位: 1010
1. 确定海明码的位数: \(2^k\geq n+k+1\)
n = 4 --> k=3
设信息位\(D_{4}D_{3}D_{2}D_{1}\)(1010)共4位, 校验位\(P_{3}P_{2}P_{1}\)共3位, 对应的海明码位\(H_{7}H_{6}H_{5}H_{4}H_{3}H_{2}H_{1}\)
2. 确定校验位的分布
校验位\(P_{i}\)放在海明位号为\(2^{i-1}\)的位置上, 其余各位为信息位
H7 H6 H5 H4 H3 H2 H1 D4 D3 D2 P3 D1 P2 P1 1 0 1 0
3. 求校验位的值
H3: 3 --> 0 1 1
H5: 5 --> 1 0 1
H6: 6 --> 1 1 0
H7: 7 --> 1 1 1
\(P_{1} = H_{3}\bigoplus H_{5}\bigoplus H_{7} = D_{1}\bigoplus D_{2}\bigoplus D_{4}=0\)
\(P_{2} = H_{3}\bigoplus H_{6}\bigoplus H_{7} = D_{1}\bigoplus D_{3}\bigoplus D_{4}=1\)
\(P_{3} = H_{5}\bigoplus H_{6}\bigoplus H_{7} = D_{2}\bigoplus D_{3}\bigoplus D_{4}=0\)
4. 纠错
校验方程:
\(S_{1}=P_{1}\bigoplus D_{1}\bigoplus D_{2}\bigoplus D_{4}\)
\(S_{2}=P_{2}\bigoplus D_{1}\bigoplus D_{3}\bigoplus D_{4}\)
\(S_{3}=P_{3}\bigoplus D_{2}\bigoplus D_{3}\bigoplus D_{4}\)
接收到: 1010010 无错误
\(S_{1}=P_{1}\bigoplus D_{1}\bigoplus D_{2}\bigoplus D_{4}\) = 0
\(S_{2}=P_{2}\bigoplus D_{1}\bigoplus D_{3}\bigoplus D_{4}\) = 0
\(S_{3}=P_{3}\bigoplus D_{2}\bigoplus D_{3}\bigoplus D_{4}\) = 0
接收到: 1010000
\(S_{1}=P_{1}\bigoplus D_{1}\bigoplus D_{2}\bigoplus D_{4}\) = 0
\(S_{2}=P_{2}\bigoplus D_{1}\bigoplus D_{3}\bigoplus D_{4}\) = 1 第101位出错
\(S_{3}=P_{3}\bigoplus D_{2}\bigoplus D_{3}\bigoplus D_{4}\) = 0
循环冗余校验码(CRC码)
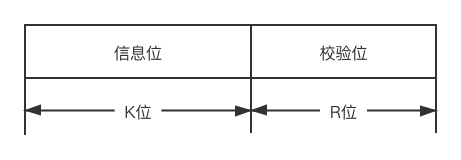
循环冗余校验码的思想: 数据发送、接收方约定一个"除数", K个信息位+R个校验位作为"被除数", 添加校验位后需要保证除法的余数为0, 收到数据后, 进行除法检查余数是否为0, 若余数非0说明出错, 则进行重传或纠错


 浙公网安备 33010602011771号
浙公网安备 33010602011771号