支撑向量机 SVM 学习笔记二 （Matlab代码）

今天调试了一下非线性核的SVM  并粗略显示一下分界线

 

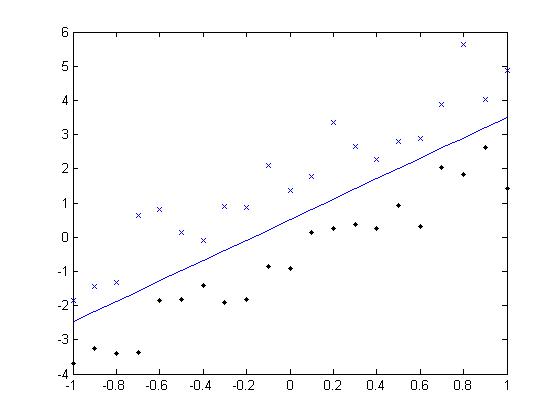
线性核  分界线

 

 

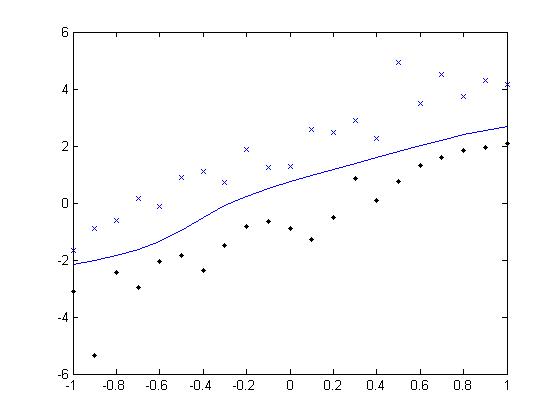
径向基核  分界线             可以看出非线性核可以拟合非线性曲线（对应 核空间中的线性曲线）

 

 

 

代码如下  还有部分小bug  例如有时候随机生成的数据 对应奇异矩阵  解二次规划 解不出来    此时可以重新运行

 

代码

 1function Result=CalcKernel(kernel,X,Y)
 2
 3
 4dimensionX=size(X);
 5m=dimensionX(1);
 6
 7
 8dimensionY=size(Y);
 9n=dimensionY(1);
10
11
12
13Result=zeros(m,n);
14
15if strcmp(kernel.type,'linear')==1
16    
17    for row=1:m
18        for col=1:n
19            Result(row,col)=X(row,:)*Y(col,:)';
20        end
21    end
22end
23
24
25if strcmp(kernel.type,'q-order polynomial kernel')==1
26    
27    q=kernel.value;
28    
29    for row=1:m
30        for col=1:n         
31            Result(row,col)=(X(row,:)*Y(col,:)' +1)^q;
32        end
33    end
34end
35
36
37if strcmp(kernel.type,'Radial basis kernel')==1
38    
39    q=2*kernel.value*kernel.value;
40    
41    for row=1:m
42        for col=1:n         
43            t=X(row,:)-Y(col,:);
44            Result(row,col)=exp(-t*t'/q);
45        end
46    end
47end
48
49

 

 

 

 1function result=CalcValueBySVM(svm, x)
 2
 3
 4result=svm.b;
 5
 6n=size(svm.y);
 7
 8for j=1:n
 9    result=result+ svm.a(j)*svm.y(j)*CalcKernel(svm.ker, x, svm.x(j,:));
10end
11
12
13

 

 

 1
 2function SVM_Test
 3
 4
 5clear all
 6% ------------------------------------------------------------%
 7% 构造两类训练数据集    以 y=ax^2+ b*x+c 为分界线   shift   
 8%  if a==0  then it is a line
 9
10a=0;
11b=3;
12c=0.5;
13
14shift=0.5;
15
16b1=0.5;       
17
18xx=-1:0.1:1;
19
20n = length(xx);
21
22x1=zeros(n,2);
23x2=zeros(n,2);
24
25x1(:,1) = xx';
26x2(:,1)=xx';
27
28
29
30x1(:,2)=a*x1(:,1).*x1(:,1)+b*x1(:,1)+c + shift+   abs(randn(n,1)) ;
31x2(:,2)=a*x2(:,1).*x2(:,1)+b*x2(:,1)+c - shift-  abs(randn(n,1)) ;
32
33y1 = ones(n,1);
34y2 = -ones(n,1);
35
36figure;
37plot(x1(:,1),x1(:,2),'bx',x2(:,1),x2(:,2),'k.');
38hold on;
39
40X = [x1;x2]; % 训练样本
41Y = [y1;y2]; % 训练目标,n×1的矩阵,n为样本个数,值为+1或-1
42
43
44
45% ------------------------------------------------------------%
46
47%ker=struct('type','linear');
48ker=struct('type','Radial basis kernel','value',1);
49
50svm=SVM_DivideTwoClass(ker,X,Y)
51
52
53
54
55
56%plot the  decision function curve
57
58for i=1:n
59
60    tx1=x1(i,1);    
61    tx2=a*tx1*tx1+b*tx1+c;    
62      
63    min=1000;
64    
65    for step=-2:0.01:2  
66           
67        tx=[tx1,tx2+step];      
68        
69        f=CalcValueBySVM(svm,tx);
70        
71        if(abs(f)<min)
72            min=abs(f);            
73            decisionCurve(i,:)=tx;
74        end
75    end
76end
77
78
79plot(decisionCurve(:,1),decisionCurve(:,2));    
80
81
82
83 
84 
85 for i=1:2*n
86     f=CalcValueBySVM(svm,X(i,:));
87    
88     YY(i)=sign(f);        
89 end
90 YY=YY'
91
92

 

 补充以前漏的，呵呵，刚刚调试出来的

%---------------- author: feathersky----------------

function svm=SVM_DivideTwoClass(ker, X,Y)

% 解二次优化方城
n = length(Y);
 %H = (Y*Y').*(X*X'); % liner kernel
H = (Y*Y').*CalcKernel(ker,X,X); %  kernel
f = -ones(n,1);
A = [];
b = [];
Aeq = Y';
beq = 0;
lb = zeros(n,1);
ub = 1000*ones(n,1);
a0 = zeros(n,1);
options = optimset;
options.LargeScale = 'off';
options.Display = 'off';
[a,fval,eXitflag,output,lambda] = quadprog(H,f,A,b,Aeq,beq,lb,ub,a0,options);
eXitflag

svm.ker=ker;
svm.x=X;
svm.y=Y;
svm.a=a;



% aLarge=find(a>0.01);    %找到第一个不等于0的a ,   
% j=aLarge(1);
% svm.b=Y(j)-CalcKernel(ker,X(j,:),w);


% ------------------------------------------------------------%%
% 求 b
epsilon = 1e-8; % 如果小于此值则认为是0
i_sv = find(a>epsilon); % 支持向量下标
tmp = (Y.*a)'*CalcKernel(ker,X,X(i_sv,:)); % 行向量
b = 1./Y(i_sv)-tmp';
b = mean(b);
svm.b=b
fprintf('Construct function Y = sign(tmp+b):')

% ------------------------------------------------------------%