梯度下降法

梯度下降法用处：寻找目标函数最小化的方法。

也就是求函数的局部最小值。

梯度的数学解释：梯度：https://baike.baidu.com/item/%E6%A2%AF%E5%BA%A6/13014729?fr=aladdin

      梯度下降法的简单解释：

梯度下降法就好比一个蒙着眼睛的人下山，每次在负梯度最大的方向，向前走一步，走出一步后，比较前后的的落差，若落差小于一定阈值，则认为到达山谷，若落差大于阈值，则继续向前走，直到到达山谷。

 

 

 数学公式：

 

 

也可以这样表示

 

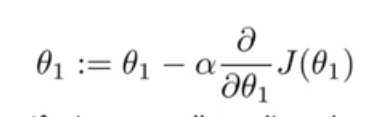
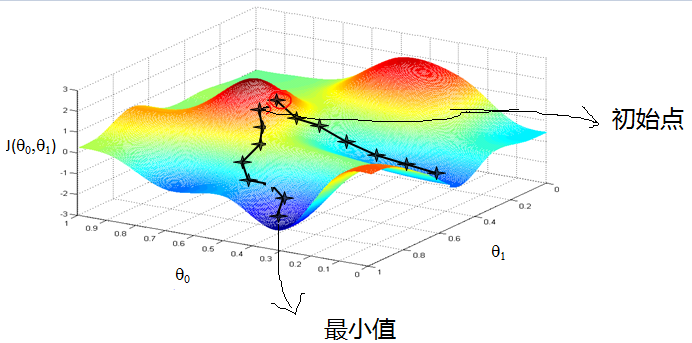
 J是关于θ的一个函数，我们当前所处的位置为θ₀点，要从这个位置走到J的最小值点，也就是山底。首先我们先确定前进的方向，也就是梯度的方向，然后走一段距离的步长，

也就是α走完这个段步长，就到达了θ1​这个点。

 

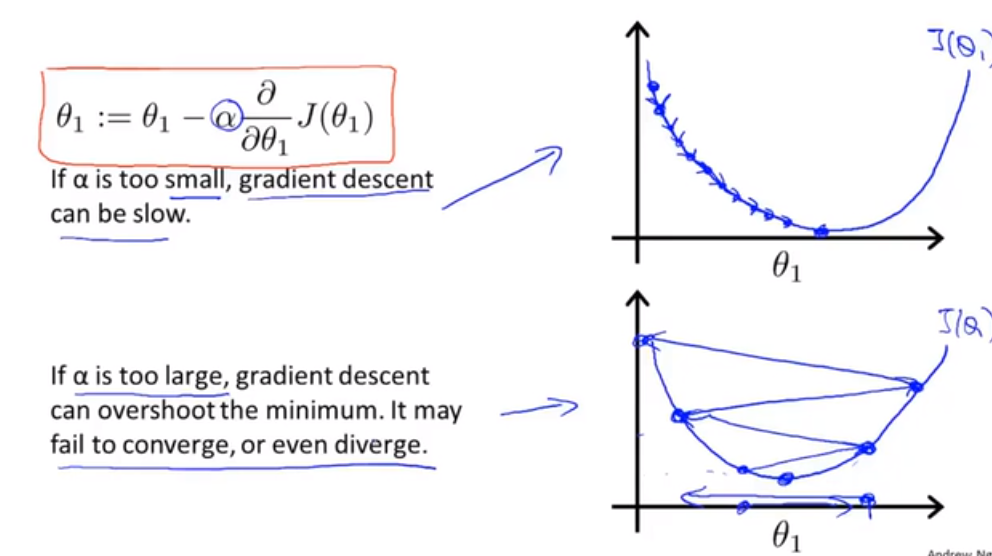
α太小，可能导致迟迟走不到最低点，太大，会导致错过最低点！

在梯度下降法中调优比较重要的是3个因素，步长、初始值、归一化。

1. 步长：步长太小，收敛慢，步长太大，会远离最优解。所以需要从小到大，分别测试，选出一个最优解。
2. 初始值：随机选取初始值，当损失函数是非凸函数时，找到的解可能是局部最优解，需要多测试几次，从局部最优解中选出最优解。当损失函数是凸函数时，得到的解就是最优解。
3. 归一化：如果不归一化，会收敛的很慢，会形成之字的路线。

由此可以看出梯度下降法的不同方法（有多种梯度下降法）就是根据这3个因素的选取来命名的。