SIFT算法原理（3）-确定关键点的主方位，构建关键点描述符

介绍官网：https://docs.opencv.org/3.0-beta/doc/py_tutorials/py_feature2d/py_sift_intro/py_sift_intro.html

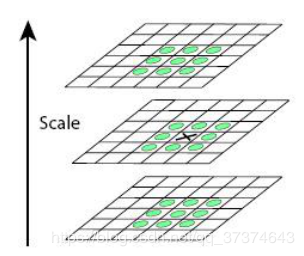
在极值点的精确定位后，还需要为找到的特征点进行方向匹配；

特征点方向分配：

   可参考：SIFT算法详解和SIFT算法原理详解

对于在DOG金字塔中检测出的关键点点，采集其所在高斯金字塔图像3σ领域窗口内像素的梯度和方向分布特征。梯度的模值和方向如下：

 

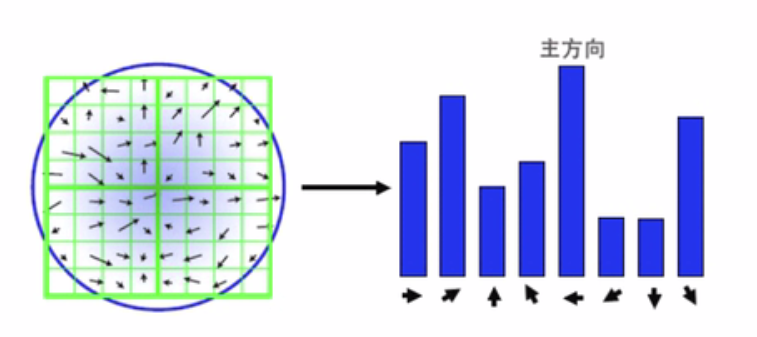
也就是说我们在高斯差分图中找到了极值点，再回到原来的高斯金字塔图中寻找与σ（尺度）相近的高斯图像， 在以关键点为中心的邻域窗口内采样，并用直方图统计邻域像素的梯度方向。梯度直方图的范围是0～360度，其中每10度一个方向，总共36个方向。直方图的峰值则代表了该关键点处邻域梯度的主方向，即作为该关键点的方向。

        考虑离极值点近的方向的像素点对极值点影响较大，我们会做一个高斯滤波（1.5σ），这样就有一个权重，计算方向直方图时，需要用一个参数等于关键点所在尺度1.5倍的高斯权重窗对方向直方图进行加权，上图中用蓝色的圆形表示，中心处的蓝色较重，表示权值最大，边缘处颜色潜，表示权值小。如下图所示，该示例中为了简化给出了8方向的方向直方图计算结果，实际sift创始人David Lowe的原论文中采用36方向的直方图。

权值为幅度m(x,y )和贡献因子的乘积。贡献因子是采样点到关键点（窗口中心）距离的量度，距离越大，贡献因子越小.直方图的峰值代表了该关键点处邻域梯度的主方向.

 

 

 

特征点主方向的确定

方向直方图的峰值则代表了该特征点处邻域梯度的方向，以直方图中最大值作为该关键点的主方向。为了增强匹配的鲁棒性，只保留峰值大于主方向峰值80％的方向（另一个方向的直方图的幅值大于主方向峰值80％的方向）作为该关键点的辅方向。因此，对于同一梯度值的多个峰值的关键点位置，在相同位置和尺度将会有多个关键点被创建但方向不同。仅有15％的关键点被赋予多个方向，但可以明显的提高关键点匹配的稳定性。实际编程实现中，就是把该关键点复制成多份关键点，并将方向值分别赋给这些复制后的关键点，并且，离散的梯度方向直方图要进行插值拟合处理，来求得更精确的方向角度值。

 

为了防止某个梯度方向角度因受到噪声的干扰而突变，我们还需要对梯度方向直方图进行平滑处理。Opencv  所使用的平滑公式为：

其中i∈[0,35],h 和H 分别表示平滑前和平滑后的直方图。由于角度是循环的，即0⁰=360⁰，如果出现h(j)，j超出了(0,…,35)的范围，那么可以通过圆周循环的方法找到它所对应的、在0⁰=360⁰之间的值，如h(-1) = h(35)。

梯度直方图的抛物线插值

 

 

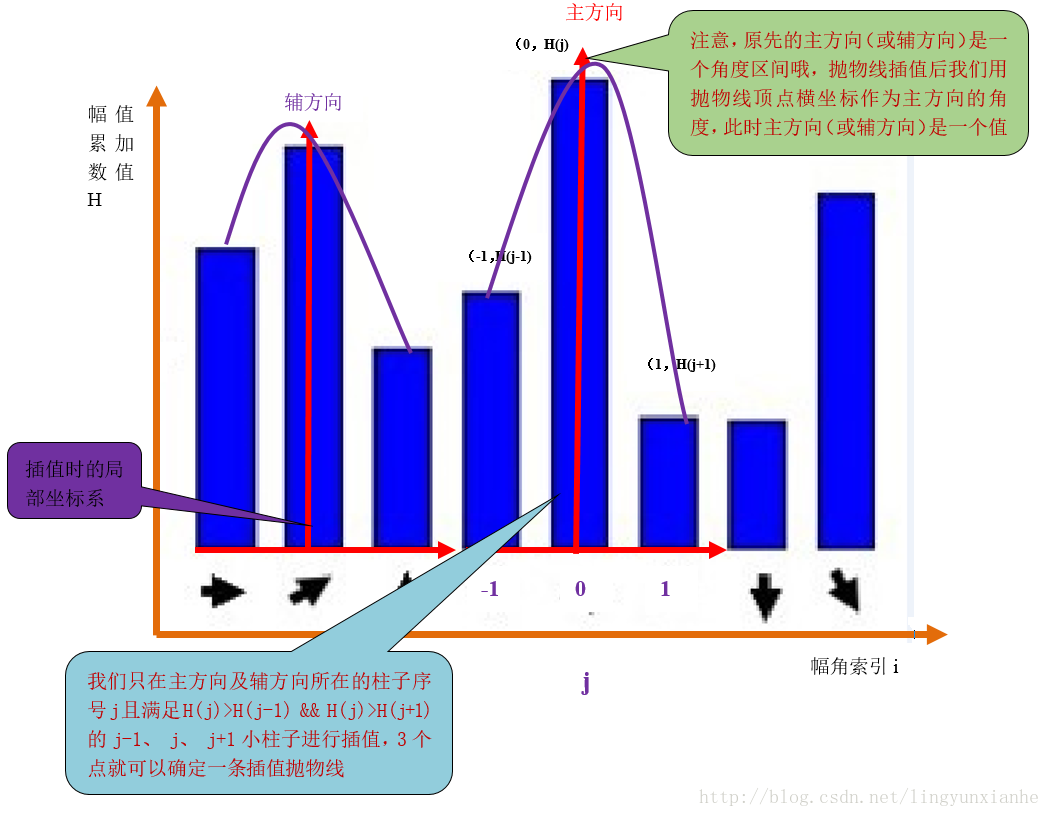
假设我们在第i个小柱子要找一个精确的方向，那么由上面分析知道：

设插值抛物线方程为h(t)=at²+bt+c,其中a、b、c为抛物线的系数，t为自变量，t∈[-1,1],此抛物线求导并令它等于0。

即h(t)´=0 得t_max=-b/(2a)

现在把这三个插值点带入方程可得：

 

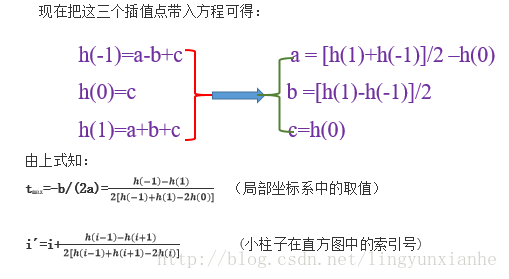
得到特征点的主方向后，对于每个特征点可以得到三个信息(x,y,σ,θ)，即位置、尺度和方向。由此可以确定一个SIFT特征区域，一个SIFT特征区域由三个值表示，中心表示特征点位置，半径表示关键点的尺度，箭头表示主方向。具有多个方向的关键点可以被复制成多份，然后将方向值分别赋给复制后的特征点，一个特征点就产生了多个坐标、尺度相等，但是方向不同的特征点。

构建关键点描述符

上面我们已经找到图片的关键点，但是我们只找到一个图片的关键点是不可以的，必须找到两个图片的关键点并把他们匹配起来，因此我们就需要用描述符将其匹配；

那么描述符是什么呢？

描述符是一组向量

       使用一组向量来描述关键点也就是生成特征点描述子，这个描述符不只包含特征点，也含有特征点周围对其有贡献的像素点。描述子应具有较高的独立性，以保证匹配率。
特征描述符的生成大致有三个步骤：
1.校正旋转主方向，确保旋转不变性。

 

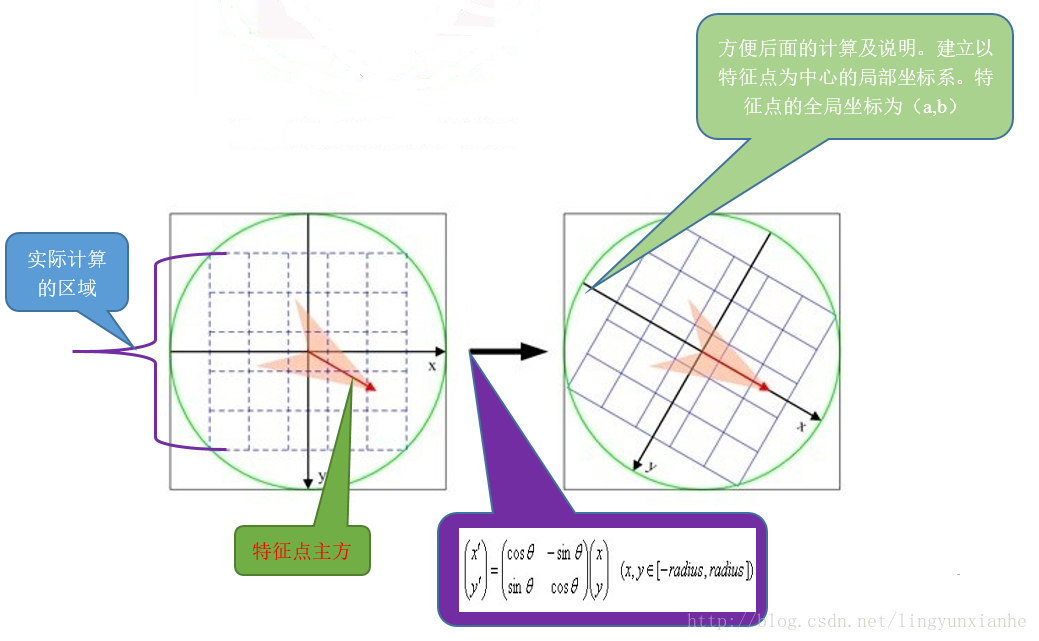
为了保证特征矢量的旋转不变性，要以特征点为中心，在附近邻域内将坐标轴旋转θ（特征点的主方向）角度，即将坐标轴旋转为特征点的主方向。旋转后邻域内像素的新坐标为：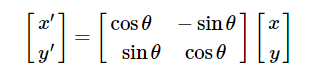

参考：为什么拉普拉斯算子具有旋转不变性

梯度直方图的生成

将邻域内的采样点分配到对应的子区域内，将子区域内的梯度值分配到8个方向上，计算其权值。

旋转后的采样点 落在子区域的下标为

 

 

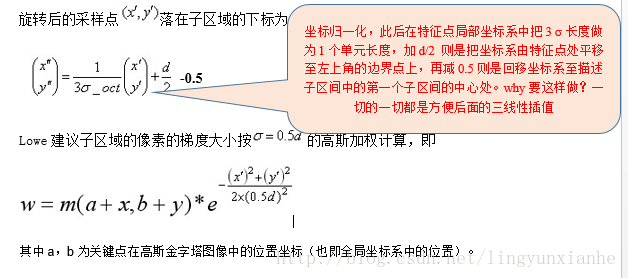
2.生成描述子，最终形成一个128维的特征向量 

旋转后以主方向为中心取 8×8的窗口。下图所示，左图的中央为当前关键点的位置，每个小格代表为关键点邻域所在尺度空间的一个像素，求取每个像素的梯度幅值与梯度方向，箭头方向代表该像素的梯度方向，长度代表梯度幅值，然后利用高斯窗口对其进行加权运算。最后在每个4×4的小块上绘制8个方向的梯度直方图，计算每个梯度方向的累加值，即可形成一个种子点，如右图所示。每个特征点由4个种子点组成，每个种子点有8个方向的向量信息。这种邻域方向性信息联合增强了算法的抗噪声能力，同时对于含有定位误差的特征匹配也提供了比较理性的容错性。

 

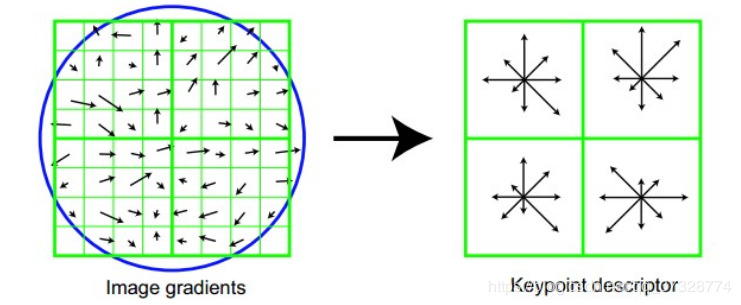
 与求主方向不同，此时每个种子区域的梯度直方图在0-360之间划分为8个方向区间，每个区间为45度，即每个种子点有8个方向的梯度强度信息。
在实际的计算过程中，为了增强匹配的稳健性，Lowe建议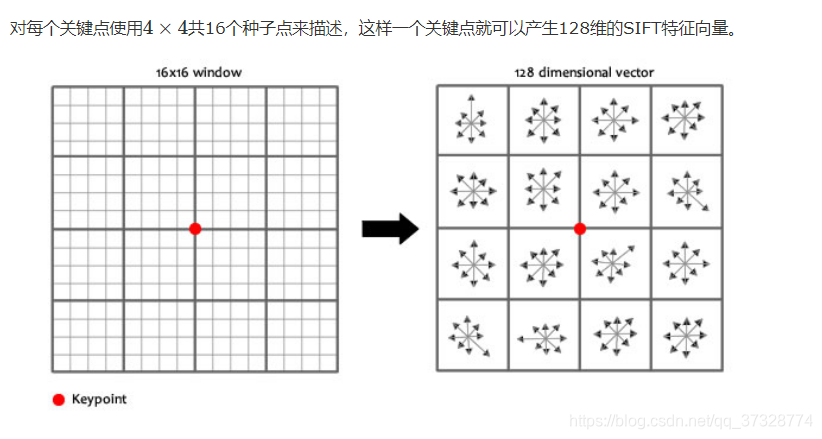
通过对特征点周围的像素进行分块，计算块内梯度直方图，生成具有独特性的向量，这个向量是该区域图像信息的一种抽象，具有唯一性。

3.归一化处理，将特征向量长度进行归一化处理，进一步去除光照的影响。

在大佬论文中使用三线差值？（这一部分占时没看太懂）

 

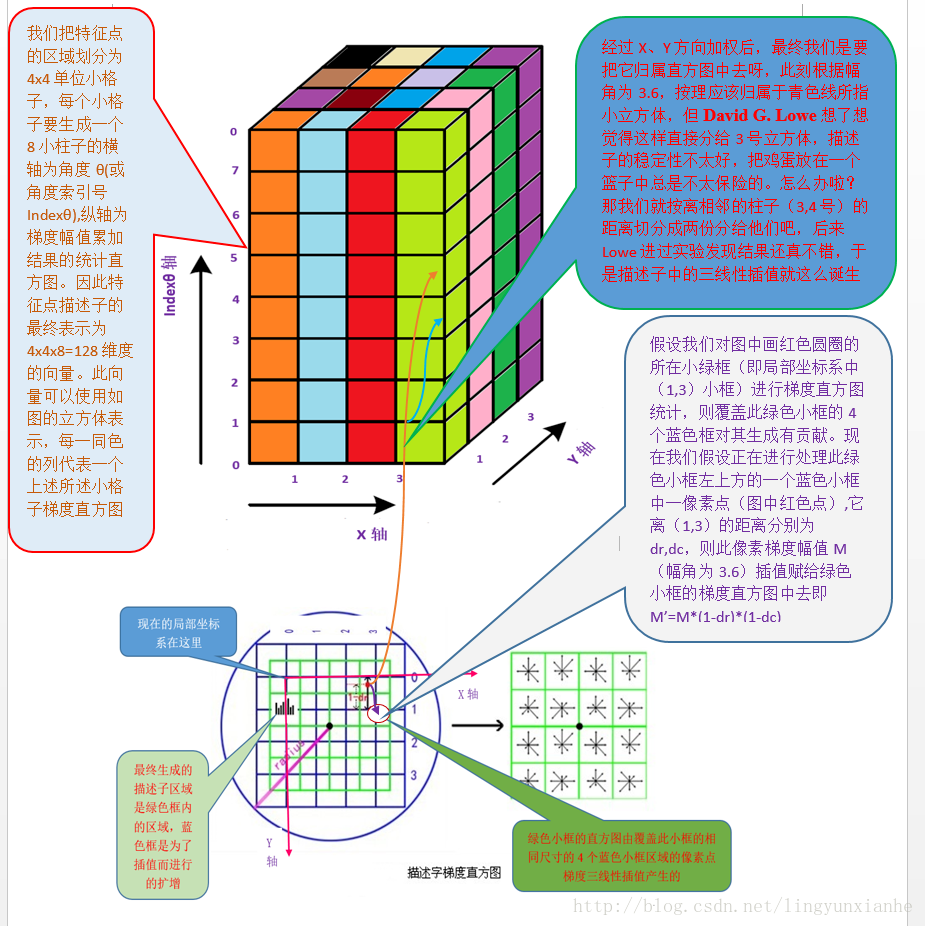
采样点在子区域中的下标(x'',y'')  (图中蓝色窗口内红色点)线性插值，计算其对每个种子点的贡献。如图中的红色点，落在第0行和第1行之间，对这两行都有贡献。对第0行第3列种子点的贡献因子为dr，对第1行第3列的贡献因子为1-dr，同理，对邻近两列的贡献因子为dc和1-dc，对邻近两个方向的贡献因子为do和1-do。则最终累加在每个方向上的梯度大小为：

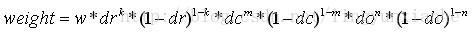
其中k，m，n为0（像素点超出了对要插值区间的四个邻近子区间所在范围）或为1（像素点处在对要插值区间的四个邻近子区间之一所在范围）。 

特征描述子

如上统计的4*4*8=128个梯度信息即为该关键点的特征向量。
      特征向量形成后，为了去除光照变化的影响，需要对它们进行归一化处理，对于图像灰度值整体漂移，图像各点的梯度是邻域像素相减得到，所以也能去除。得到的描述子向量为H=(h1,h2,.......,h128)，归一化后的特征向量为L=(L1,L2,......,L128)，则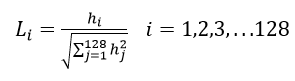

描述子的门限化

非线性光照，相机饱和度变化对造成某些方向的梯度值过大，而对方向的影响微弱。因此设置门限值(向量归一化后，一般取0.2)截断较大的梯度值(大于0.2的则就令它等于0.2，小于0.2的则保持不变)。然后再进行一次归一化处理，提高特征的鉴别性。

描述子相关分析

用一组图来概括描述子的生成过程

描述子生成总括

 

 

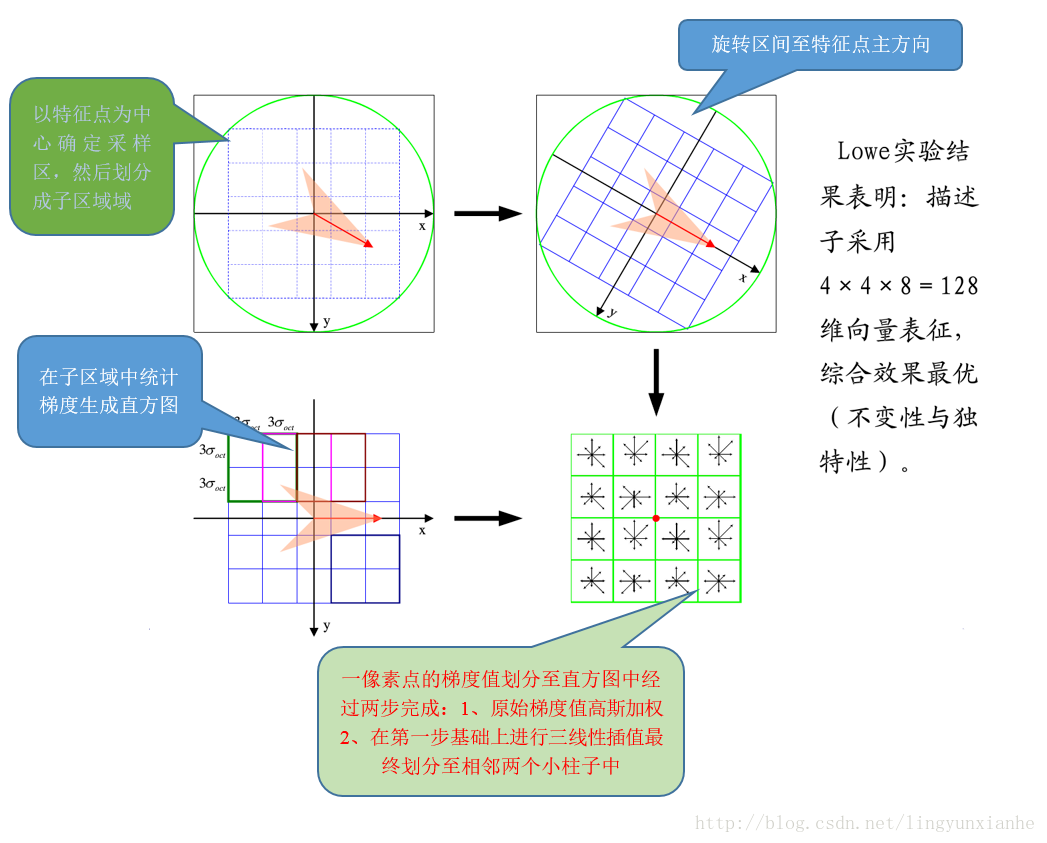
 参考：SIFT算法原理详解

https://blog.csdn.net/qq_37328774/article/details/88617952