SIFT解析(一)建立高斯金字塔
高斯金字塔是SIFT特征提取的第一步,之后特征空间中极值点的确定,都是基于高斯金字塔,因此SIFT特征学习的第一步是如何建立的高斯金字塔。
八度(octave) 简单地说八度就是在特定尺寸(长宽)下,经不同高斯核模糊的图像的集合。八度的集合是高斯金字塔。
为什么要构建高斯金字塔:
整个高斯金字塔,或者说是差分高斯金字塔是我们确定SIFT特征的基础,让我们首先想想高斯金字塔到底干了一件什么事情,他到底模仿的是什么?答案很容易确定,高斯金字塔模仿的是图像的不同的尺度,尺度应该怎样理解?对于一副图像,你近距离观察图像,与你在一米之外观察,看到的图像效果是不同的,前者比较清晰,后者比较模糊,前者比较大,后者比较小,通过前者能看到图像的一些细节信息,通过后者能看到图像的一些轮廓的信息,这就是图像的尺度,图像的尺度是自然存在的,并不是人为创造的。好了,到这里我们明白了,其实以前对一幅图像的处理还是比较单调的,因为我们的关注点只落在二维空间,并没有考虑到“图像的纵深”这样一个概念,如果将这些内容考虑进去我们是不是会得到更多以前在二维空间中没有得到的信息呢?于是高斯金字塔横空出世了,它就是为了在二维图像的基础之上,榨取出图像中自然存在的另一个维度:尺度。因为高斯核是唯一的线性核,也就是说使用高斯核对图像模糊不会引入其他噪声,因此就选用了高斯核来构建图像的尺度。
下图两幅图像是典型的图像高斯金字塔,这就是模仿的图像离你远去时在你视网膜上的成像,图像分别以动态方式表示。

高斯金字塔的构建步骤:
根据Lowe的论文,高斯金字塔的构建还是比较简单的,高斯卷积和是尺度变换的唯一的线性核。
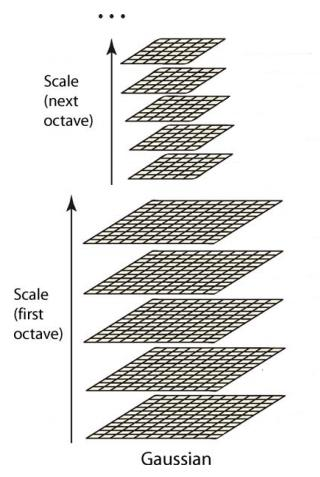
构建出的金字塔如下图所示:

图1
也就是用不同的ó来进行高斯卷积,Octave1进行ó1的高斯模糊得到的图片在进行降采样;得到Octave2最底层(如上图...号下的图片),此图片进行ó2的高斯模糊得到的图片在进行降采样;如此循环;得到高斯金字塔;
图像的金字塔模型是指,将原始图像不断降阶采样,得到一系列大小不一的图像,由大到小,从下到上构成的塔状模型。原图像为金子塔的第一层,每次降采样所得到的新图像为金字塔的一层(每层一张图像),每个金字塔共n 层。为了让尺度体现其连续性,高斯金字塔在简单降采样的基础上加上了高斯滤波。高斯金字塔上一组图像的初始图像(底层图像)是由前一组图像的倒数第三张图像隔点采样得到的。
具体可见:opencv-图像上采样和降采样

在同一组内,不同层图像的尺寸是一样的,后一层图像的高斯平滑因子σ是前一层图像平滑因子的k倍;
在不同组内,后一组第一个图像是前一组倒数第三个图像的二分之一采样,图像大小是前一组的一半;
以上已经从人视觉感知的角度让大家感性认识了“尺度”,上文也提到使用高斯核来实现尺度的变换,那么具体实现过程中,尺度体现在哪里?是如何量化的呢?高斯核的ó如何确定呢?
在图1中,S表示每组提取多少层,s表示第几层,o第几个八度;
八度(octave) 简单地说八度就是在特定尺寸(长宽)下,经不同高斯核模糊的图像的集合。八度的集合是高斯金字塔。
在高斯金字塔中,两个变量很重要,即第几个八度(o)和八度中的第几层(s),这两个量合起来(o,s)就构成了高斯金字塔的尺度空间。尺度空间也不难理解,首先一个八度中图像的长和宽是相等的,即变量o控制的是塔中尺寸这个尺度;区分同一个尺寸尺度下的图像,就需要s了,s控制了一个八度中不同的模糊程度。这样(o,s)就能够确定高斯金字塔中的唯一一幅图像了,这是个三维空间,两维坐标,一维是图像。
根据lowe的论文,(o,s)作用于一幅图像是通过公式
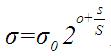
确定的。通过公式也可以看出,尺度空间是连续的,两个变量控制着δ的值,其中在第一个八度中有 1<(o+s/S)<=2 ,同理在第二个八度中有2<(o+s/S)<=3,以此类推,δ中的关键部分(o+s/S)部分是逐渐增大的(具体实现时,有些高斯金字塔中这个值是增大,但不是逐渐均匀增大,只能说是连续的)。
上图中第一个八度的中图像的尺度分别是δ,kδ,k^2δ......,第二个八度的尺度分别是2δ,2kδ,2k^2δ........,同理第三个八度的尺度分别是4δ,4kδ,4k^2δ........。这个序列是通过下式来确定的:
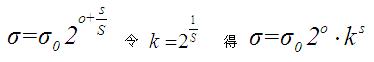
所以每增加一级八度,δ都要扩大2倍,在一个八度中,k的上标s来区分不同的高斯核。
至此,高斯金字塔中的尺度空间已经说得差不多了,包括尺度是什么,包括高斯金字塔中尺度的连续性,后文将详细说明尺度空间的连续性。
高斯差分金字塔
上面可以知道高斯金字塔构建过程中,一般首先将图像扩大一倍,在扩大的图像的基础之上构建高斯金字塔,然后对该尺寸下图像进行高斯模糊,几幅模糊之后的图像集合构成了一个八度,然后对该八度下的最模糊的一幅图像进行下采样的过程,长和宽分别缩短一倍,图像面积变为原来四分之一。这幅图像就是下一个八度的初始图像,在初始图像图像的基础上完成属于这个八度的高斯模糊处理,以此类推完成整个算法所需要的所有八度构建,这样这个高斯金字塔就构建出来了。
这样每一组中就有几幅高斯金字塔的图片;
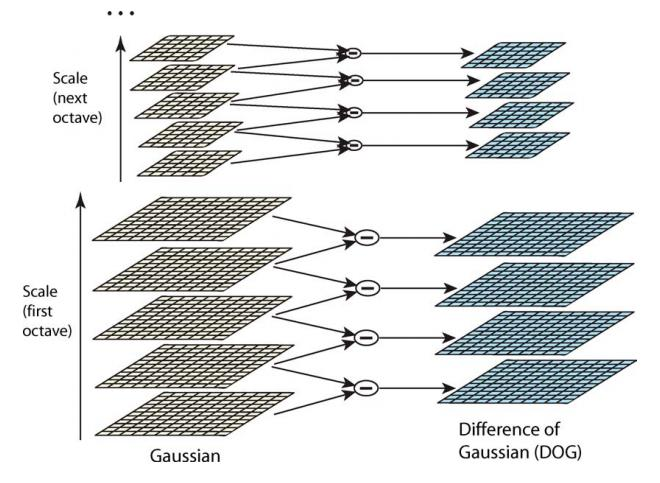
构建高斯金字塔是为了后续构建差分高斯金字塔。对同一个八度的两幅相邻的图像做差得到插值图像,所有八度的这些插值图像的集合,就构成了差分高斯金字塔。过程如下图所示,差分高斯金字塔的好处是为后续的特征点的提取提供了方便。
【尺度空间】
图像的尺度空间解决的问题是如何对图像在所有尺度下描述的问题。
在高斯金字塔中一共生成O组L层不同尺度的图像,这两个量合起来(O,L)就构成了高斯金字塔的尺度空间,也就是说以高斯金字塔的组O作为二维坐标系的一个坐标,不同层L作为另一个坐标,则给定的一组坐标(O,L)就可以唯一确定高斯金字塔中的一幅图像。
尺度空间的形象表述:
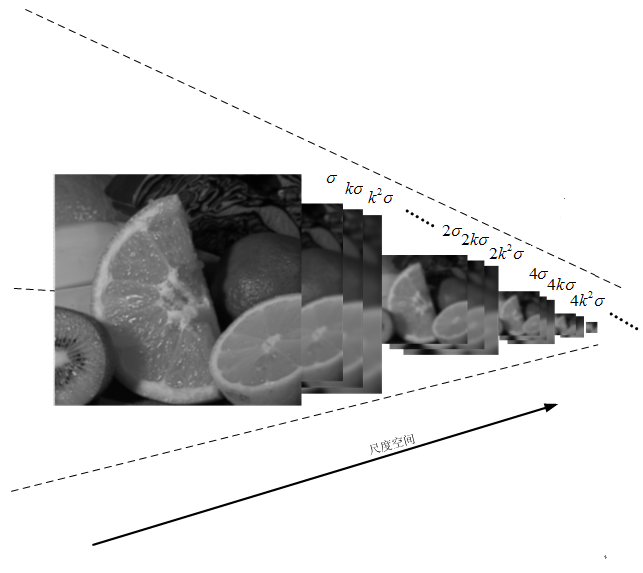
上图中尺度空间中k前的系数n表示的是第一组图像尺寸是当前组图像尺寸的n倍。
【DoG 角点检测】
DoG (Difference of Gaussian)是灰度图像增强和角点检测的方法,其做法较简单,证明较复杂,具体讲解如下:Difference of Gaussian(DOG)是高斯函数的差分。我们已经知道可以通过将图像与高斯函数进行卷积得到一幅图像的低通滤波结果,即去噪过程,这里的Gaussian和高斯低通滤波器的高斯一样,是一个函数,即为正态分布函数。

那么difference of Gaussian 即高斯函数差分是两幅高斯图像的差,
一维表示: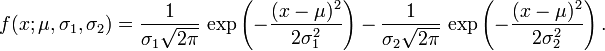
二维表示: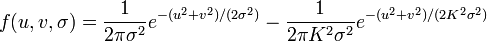
具体到图像处理来讲,就是将两幅图像在不同参数下的高斯滤波结果相减,得到DoG图。
参考文章:
图像金字塔、高斯金字塔、差分金字塔(DOG金字塔)、尺度空间、DoG (Difference of Gaussian)角点检测
DoG (Difference of Gaussian)角点检测
Sift中尺度空间、高斯金字塔、差分金字塔(DOG金字塔)、图像金字塔



