opencv-图像上采样和降采样

 

 

 

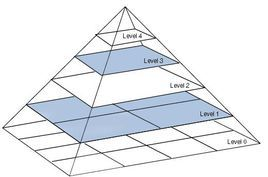
图像金字塔

      图像金字塔是图像多尺度表达的一种，是一种以多分辨率来解释图像的有效但概念简单的结构。一幅图像的金字塔是一系列以金字塔形状排列的分辨率逐步降低，且来源于同一张原始图的图像集合。其通过梯次向下采样获得，直到达到某个终止条件才停止采样。我们将一层一层的图像比喻成金字塔，层级越高，则图像越小，分辨率越低。

降采样，即是采样点数减少。对于一幅N*M的图像来说，如果降采样系数为k,则即是在原图中 每行每列每隔k个点取一个点组成一幅图像。降采样很容易实现. 
升采样，也即插值。对于图像来说即是二维插值。如果升采样系数为k,即在原图n与n+1两点之间插入k-1个点，使其构成k分。二维插值即在每行插完之后对于每列也进行插值。 
插 值的方法分为很多种，一般主要从时域和频域两个角度考虑。对于时域插值，最为简单的是线性插值。除此之外，Hermite插值，样条插值等等均可以从有关 数值分析书中找到公式，直接代入运算即可。对于频域，根据傅里叶变换性质可知，在频域补零等价于时域插值。所以，可以通过在频域补零的多少实现插值运 算。

高斯金字塔采样相关API
（1）上采样(cv::pyrUp) – 放大（zoom in），向底端发展

pyrUp(Mat src, Mat dst, Size(src.cols*2, src.rows*2)); //生成的图像是原图在宽与高各放大两倍

pyrUp(src, dst, Size(src.cols * 2, src.rows * 2)); //上采样


（2）降采样 (cv::pyrDown) – 缩小（zoom out），向顶端发展

pyrDown(Mat src, Mat dst, Size(src.cols/2, src.rows/2)); //生成的图像是原图在宽与高各缩小1/2

pyrDown(src, dst2, Size(src.cols / 2, src.rows / 2)); //降采样

高斯金字塔–降采样

• 高斯金字塔从底向上，逐层降采样取得，不能跨域越层；
• 对当前层删除偶数行与列就得到降采样后上一层的图片；
• 降采样后的图像大小是之前图像大小的1414；
• 高斯金字塔生成步骤： 
  
  • ①进行高斯模糊；
  • ②删除偶数行与列。

 

 

 

#include <opencv2/opencv.hpp>
#include <iostream> 
#include <math.h>
using namespace cv;      //使用cv命名空间
int main(int argc, char** argv) {    //argc 表示命令行输入参数的个数（以空白符分隔），argv中存储了所有的命令行参数
	Mat src, dst, dst2;
	src = imread("E:\\VS2015Opencv\\vs2015\\project\\picture\\091.jpg");
	if (src.empty()) {
		printf("could not load image...\n");
		return -1;
	}
	namedWindow("input image", CV_WINDOW_AUTOSIZE);
	imshow("input image", src);
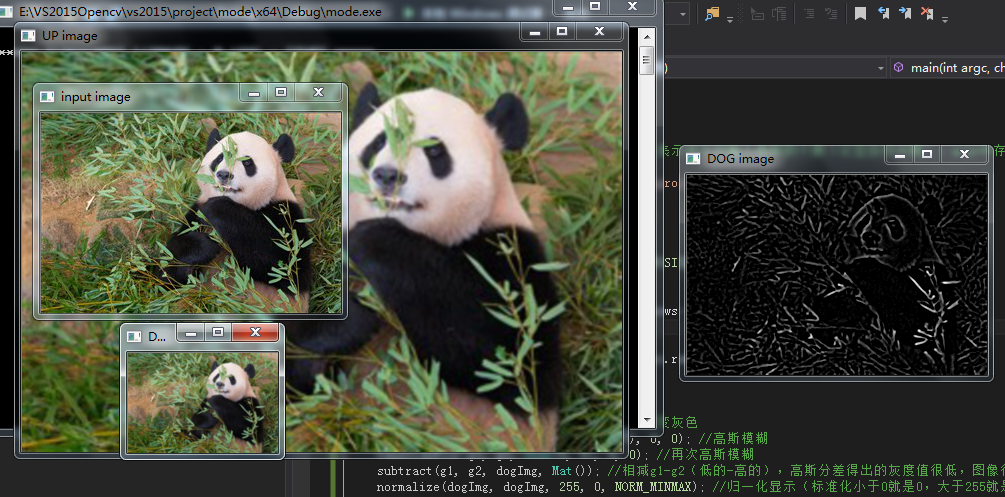
	/*上采样*/
	pyrUp(src, dst, Size(src.cols * 2, src.rows * 2)); //上采样
	imshow("UP image", dst);
	/*降采样*/
	pyrDown(src, dst2, Size(src.cols / 2, src.rows / 2)); //降采样
	imshow("DOWN image", dst2);
	/*高斯不同DOG*/
	Mat gray_src, g1, g2, dogImg;
	cvtColor(src, gray_src, CV_BGR2GRAY); //变灰色
	GaussianBlur(gray_src, g1, Size(5, 5), 0, 0); //高斯模糊
	GaussianBlur(g1, g2, Size(5, 5), 0, 0); //再次高斯模糊
	subtract(g1, g2, dogImg, Mat()); //相减g1-g2（低的-高的），高斯分差得出的灰度值很低，图像很暗
	normalize(dogImg, dogImg, 255, 0, NORM_MINMAX); //归一化显示（标准化小于0就是0，大于255就是255），最大值255，最小值0，最大最小类型
	imshow("DOG image", dogImg);
	waitKey(0);
	return 0;
}　　

参考文章：

https://blog.csdn.net/qq_25343557/article/details/78694722

https://zhuanlan.zhihu.com/p/40489916