超参数，正则化

超参数：在机器学习中，超参数是在开始学习过程之前定义的参数，而不是通过训练得到的参数；

过拟合：神经网络模型在训练数据集上的准确率较高，但此模型在新的数据进行预测或分类时准确率较低，则说明这个模型的泛化能力差。 

正则化：在损失函数中给每个参数 w 加上权重，引入模型复杂度指标，从而抑制模型噪声，减小过拟合。 
使用正则化后，损失函数 loss 变为两项之和

                           loss = loss(y 与 y_) + REGULARIZER*loss(w) 

               其中，第一项是预测结果与标准答案之间的差距，如之前讲过的交叉熵、均方误差等；第二项是正则化计算结果。
正则化计算方法：

              

                 𝒍𝒐𝒔𝒔_𝑳𝟏 = ∑_𝒊|𝒘_𝒊| 对所有的w求和；

                 𝒍𝒐𝒔𝒔_𝑳𝟐 = ∑_𝒊|𝒘𝒊|^𝟐 对所有的w²求和；

用 Tesnsorflow 函数实现正则化：
         tf.add_to_collection('losses', tf.contrib.layers.l2_regularizer(regularizer)(w)             #把计算好的正则化w加到losses集合中
         loss = cem + tf.add_n(tf.get_collection('losses'))                                                       #把losses和cem(交叉熵）相加构成总损失函数例如： 

           用 300 个符合正态分布的点 X[x0, x1]作为数据集，根据点 X[x0, x1]计算生成标注 Y_，将数据集标注为红色点和蓝色点。 
标注规则为：当 x02 + x12 < 2 时，y_=1，标注为红色；当 x02 + x12 ≥2 时，y_=0，标注为蓝色。
我们分别用无正则化和有正则化两种方法，拟合曲线，把红色点和蓝色点分开。在实际分类时，如果前向传播输出的预测值 y 接近 1 则为红色点概率越大，接近 0 则为蓝色点概率越大，输出的预测值 y 为 0.5 是红蓝点概率分界线。

本例中需要用到matplotlib 模块：Python 中的可视化工具模块，实现函数可视化 ;下面简要讲解一下安装和使用说明；

matplotlib 模块安装：

             我的系统环境ubuntu16.04LTS,系统默认的python版本为2.7；现在安装用于数值计算和绘图的包以及Sklearn 分别是numpy scipy matplotlib pandas 和 sklearn ；apt-get命令如下

sudo apt-get install python-numpy 
sudo apt-get install python-scipy 
sudo apt-get install python-matplotlib 
sudo apt-get install python-pandas 
sudo apt-get install python-sklearn

　选择安装sudo apt-get install python-matplotlib；则安装成功；

安装成功后，在python代码中导入；

　import numpy as np

 import matplotlib.pyplot as plt

函数 plt.scatter（）：利用指定颜色实现点(x,y)的可视化
               plt.scatter (x 坐标, y 坐标, c=”颜色”)
               plt.show()

收集规定区域内所有的网格坐标点： 

              xx, yy = np.mgrid[起:止:步长, 起:止:步长] #找到规定区域以步长为分辨率的行列网格坐标点
              grid = np.c_[xx.ravel(), yy.ravel()] #收集规定区域内所有的网格坐标点
plt.contour()函数：告知 x、y 坐标和各点高度，用 levels 指定高度的点描上颜色
             plt.contour (x 轴坐标值, y 轴坐标值, 该点的高度, levels=[等高线的高度]) plt.show()

其中:

         xx,yy是对应的x，y坐标轴，

        ravel()函数实现的功能是将多维数组降位一维

        np.c_是按行连接两个矩阵，也就是将x,y轴对应坐标配对，组成矩阵

        plt.contour()函数：告知 x、y 坐标和各点高度，用 levels 指定高度的点描上颜色
        plt.contour (x 轴坐标值, y 轴坐标值, 该点的高度, levels=[等高线的高度]) plt.show()

 代码如下：

#coding:utf-8
#0导入模块 ，生成模拟数据集
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
BATCH_SIZE = 30 
seed = 2 
#基于seed产生随机数
rdm = np.random.RandomState(seed)
#随机数返回300行2列的矩阵，表示300组坐标点（x0,x1）作为输入数据集
X = rdm.randn(300,2)
#从X这个300行2列的矩阵中取出一行,判断如果两个坐标的平方和小于2，给Y赋值1，其余赋值0
#作为输入数据集的标签（正确答案）
Y_ = [int(x0*x0 + x1*x1 <2) for (x0,x1) in X]
#遍历Y中的每个元素，1赋值'red'其余赋值'blue'，这样可视化显示时人可以直观区分
Y_c = [['red' if y else 'blue'] for y in Y_]
#对数据集X和标签Y进行shape整理，第一个元素为-1表示，随第二个参数计算得到，第二个元素表示多少列，把X整理为n行2列，把Y整理为n行1列
X = np.vstack(X).reshape(-1,2)
Y_ = np.vstack(Y_).reshape(-1,1)
print X
print Y_
print Y_c
#用plt.scatter画出数据集X各行中第0列元素和第1列元素的点即各行的（x0，x1），用各行Y_c对应的值表示颜色（c是color的缩写） 
plt.scatter(X[:,0], X[:,1], c=np.squeeze(Y_c)) 
plt.show()


#定义神经网络的输入、参数和输出，定义前向传播过程 
def get_weight(shape, regularizer):
    w = tf.Variable(tf.random_normal(shape), dtype=tf.float32)
    tf.add_to_collection('losses', tf.contrib.layers.l2_regularizer(regularizer)(w))
    return w

def get_bias(shape):  
    b = tf.Variable(tf.constant(0.01, shape=shape)) 
    return b
    
x = tf.placeholder(tf.float32, shape=(None, 2))
y_ = tf.placeholder(tf.float32, shape=(None, 1))

w1 = get_weight([2,11], 0.01)    
b1 = get_bias([11])
y1 = tf.nn.relu(tf.matmul(x, w1)+b1)

w2 = get_weight([11,1], 0.01)
b2 = get_bias([1])
y = tf.matmul(y1, w2)+b2 #输出层不过激活层函数


#定义损失函数
loss_mse = tf.reduce_mean(tf.square(y-y_))
loss_total = loss_mse + tf.add_n(tf.get_collection('losses'))


#定义反向传播方法：不含正则化
train_step = tf.train.AdamOptimizer(0.0001).minimize(loss_mse)

with tf.Session() as sess:
    init_op = tf.global_variables_initializer()
    sess.run(init_op)
    STEPS = 40000
    for i in range(STEPS):
        start = (i*BATCH_SIZE) % 300
        end = start + BATCH_SIZE
        sess.run(train_step, feed_dict={x:X[start:end], y_:Y_[start:end]})
        if i % 2000 == 0:
            loss_mse_v = sess.run(loss_mse, feed_dict={x:X, y_:Y_})
            print("After %d steps, loss is: %f" %(i, loss_mse_v))
    #xx在-3到3之间以步长为0.01，yy在-3到3之间以步长0.01,生成二维网格坐标点
    xx, yy = np.mgrid[-3:3:.01, -3:3:.01]
    #将xx , yy拉直，并合并成一个2列的矩阵，得到一个网格坐标点的集合
    grid = np.c_[xx.ravel(), yy.ravel()]
    #将网格坐标点喂入神经网络 ，probs为输出
    probs = sess.run(y, feed_dict={x:grid})
    #probs的shape调整成xx的样子
    probs = probs.reshape(xx.shape)
    print "w1:\n",sess.run(w1)
    print "b1:\n",sess.run(b1)
    print "w2:\n",sess.run(w2)    
    print "b2:\n",sess.run(b2)

plt.scatter(X[:,0], X[:,1], c=np.squeeze(Y_c))
plt.contour(xx, yy, probs, levels=[.5])
plt.show()



#定义反向传播方法：包含正则化
train_step = tf.train.AdamOptimizer(0.0001).minimize(loss_total)

with tf.Session() as sess:
    init_op = tf.global_variables_initializer()
    sess.run(init_op)
    STEPS = 40000
    for i in range(STEPS):
        start = (i*BATCH_SIZE) % 300
        end = start + BATCH_SIZE
        sess.run(train_step, feed_dict={x: X[start:end], y_:Y_[start:end]})
        if i % 2000 == 0:
            loss_v = sess.run(loss_total, feed_dict={x:X,y_:Y_})
            print("After %d steps, loss is: %f" %(i, loss_v))

    xx, yy = np.mgrid[-3:3:.01, -3:3:.01]
    grid = np.c_[xx.ravel(), yy.ravel()]
    probs = sess.run(y, feed_dict={x:grid})
    probs = probs.reshape(xx.shape)
    print "w1:\n",sess.run(w1)
    print "b1:\n",sess.run(b1)
    print "w2:\n",sess.run(w2)
    print "b2:\n",sess.run(b2)

plt.scatter(X[:,0], X[:,1], c=np.squeeze(Y_c)) 
plt.contour(xx, yy, probs, levels=[.5])
plt.show()

数据集实现可视化，x0*x0 + x1*x1 <2的点显示红色，其余显示蓝色，如图

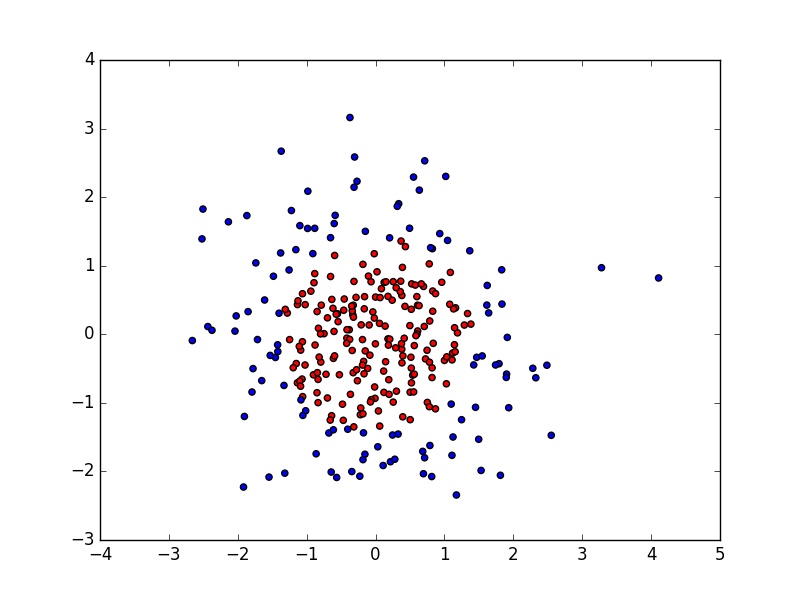
执行无正则化过程，将红色和蓝色的点分开，如下图所示；

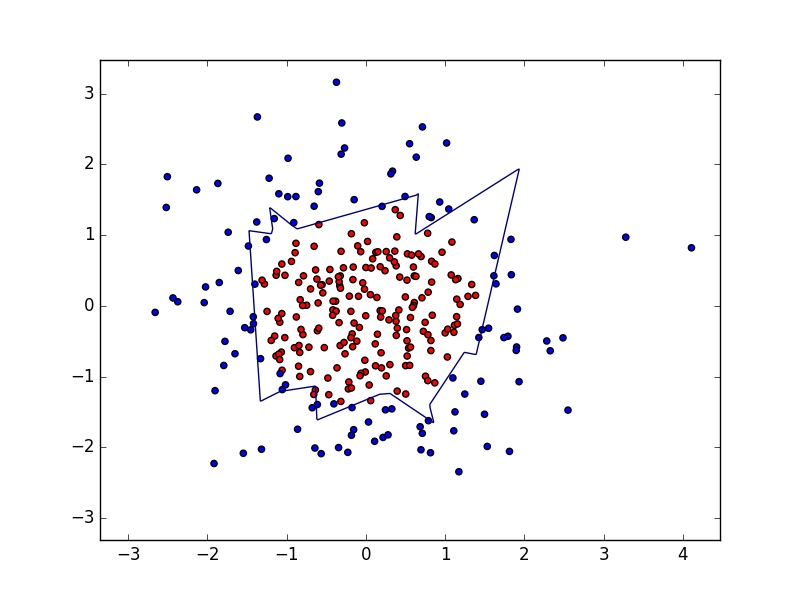
执行正则化过程，将红色和蓝色的点分开，如下图所示；

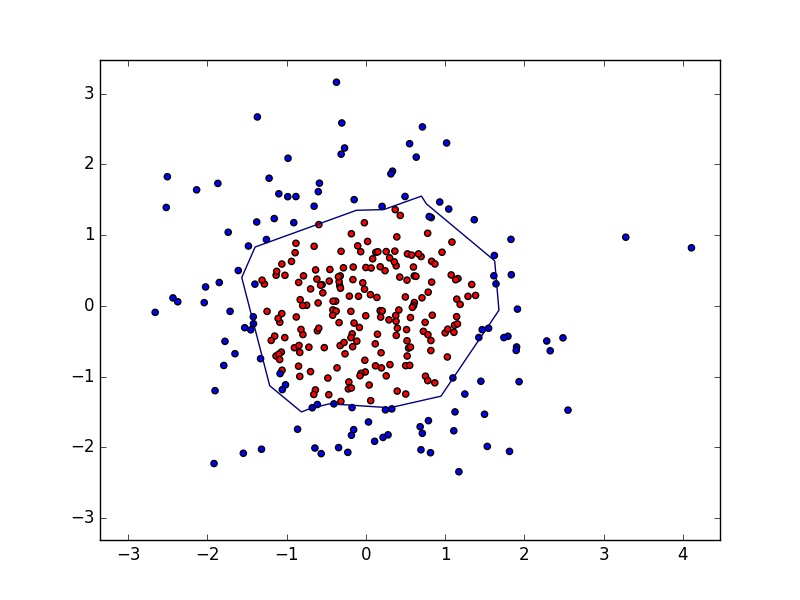
从图中可以看出，正则化的模型曲线平滑。