归并排序之非递归版及优化探讨
本文探讨的是2-路归并排序的算法,在空间复杂度上,需要与待排记录等数量的辅助空间;时间复杂度上,为O(nlogn)。相比较于快速排序与堆排序而言,归并排序的最大特点就是,它是一种稳定的排序算法。书上给出了其递归算法的实现,本人就自己写的非递归版本,在效率与优化上做一点比较。
递归版本
首先先给出递归版本的实现,编译环境:VS2012
统一定义的头文件:
/* c10-1.h 待排记录的数据类型 */
#define MAXSIZE 20 /* 一个用作示例的小顺序表的最大长度 */
typedef int KeyType; /* 定义关键字类型为整型 */
typedef struct
{
KeyType key; /* 关键字项 */
InfoType otherinfo; /* 其它数据项,具体类型在主程中定义 */
}RedType; /* 记录类型 */
typedef struct
{
RedType r[MAXSIZE+1]; /* r[0]闲置或用作哨兵单元 */
int length; /* 顺序表长度 */
}SqList; /* 顺序表类型 */
然后再给出具体的实现,附上测试:将10个关键字的记录重复测试排序一千万次,计算所需时间
/* alg10-10.c 归并排序 */ #pragma warning(disable: 4996) #include<stdio.h> #include <conio.h> typedef int InfoType; /* 定义其它数据项的类型 */ #include "C10-1.h" #include "time.h" /* c9.h 对两个数值型关键字的比较约定为如下的宏定义 */ #define EQ(a,b) ((a)==(b)) #define LT(a,b) ((a)<(b)) #define LQ(a,b) ((a)<=(b)) void Merge(RedType SR[],RedType TR[],int i,int m,int n) { /* 将有序的SR[i..m]和SR[m+1..n]归并为有序的TR[i..n] 算法10.12 */ int j,k,l; for(j=m+1,k=i;i<=m&&j<=n;++k) /* 将SR中记录由小到大地并入TR */ if LQ(SR[i].key,SR[j].key) TR[k]=SR[i++]; else TR[k]=SR[j++]; if(i<=m) for(l=0;l<=m-i;l++) TR[k+l]=SR[i+l]; /* 将剩余的SR[i..m]复制到TR */ if(j<=n) for(l=0;l<=n-j;l++) TR[k+l]=SR[j+l]; /* 将剩余的SR[j..n]复制到TR */ } void MSort(RedType SR[],RedType TR1[],int s, int t) { /* 将SR[s..t]归并排序为TR1[s..t]。算法10.13 */ int m; RedType TR2[MAXSIZE+1]; if(s==t) TR1[s]=SR[s]; else { m=(s+t)/2; /* 将SR[s..t]平分为SR[s..m]和SR[m+1..t] */ MSort(SR,TR2,s,m); /* 递归地将SR[s..m]归并为有序的TR2[s..m] */ MSort(SR,TR2,m+1,t); /* 递归地将SR[m+1..t]归并为有序的TR2[m+1..t] */ Merge(TR2,TR1,s,m,t); /* 将TR2[s..m]和TR2[m+1..t]归并到TR1[s..t] */ } } void MergeSort(SqList *L) { /* 对顺序表L作归并排序。算法10.14 */ MSort((*L).r,(*L).r,1,(*L).length); } void print(SqList L) { int i; for(i=1;i<=L.length;i++) printf("(%d,%d)",L.r[i].key,L.r[i].otherinfo); printf("\n"); } #define N 10 void main() { RedType d[N]={{49,1},{38,2},{97,3},{32,4},{76,5},{13,6},{12,7},{2,8},{3,9},{45,10}}; SqList l; int i,t; clock_t a,b; double c; loop: for(i=0;i<N;i++) l.r[i+1]=d[i]; l.length=N; printf("排序前:\n"); print(l); a=clock(); /*测试用时*/ for(i=0;i<10000000;i++) { for(t=0;t<N;t++) l.r[t+1]=d[t]; MergeSort(&l); } b=clock(); c=(double)(b-a)/1000; printf("用时为%f秒,%d,%d\n",c,a,b); printf("排序后:\n"); print(l); while(1) { printf("是否继续(y/n):"); if((t=getche(),printf("\n\n"),t)=='y') goto loop; if(t=='n') break; } }
在debug版本上,所需时间大约为15.0s,但在release版优化后,就只需2.74s


非递归版本
下面就晒出自己的非递归版本,由于代码写的实在垃圾,无论是debug,还是release都毫无优势,就不做具体分析了,读者自行查看

/* alg10-10.c 归并排序(非递归版) */ #pragma warning(disable: 4996) #include <stdio.h> #include <conio.h> #include <malloc.h> typedef int InfoType; /* 定义其它数据项的类型 */ #include "C10-1.h" #include "time.h" #define N 10 /* c9.h 对两个数值型关键字的比较约定为如下的宏定义 */ #define EQ(a,b) ((a)==(b)) #define LT(a,b) ((a)<(b)) #define LQ(a,b) ((a)<=(b)) void Merge(RedType SR[],RedType TR[],int i,int m,int n) { /* 将有序的SR[i..m]和SR[m+1..n]归并为有序的TR[i..n] 算法10.12 */ int j,k,l; for(j=m+1,k=i;i<=m&&j<=n;++k) /* 将SR中记录由小到大地并入TR */ if LQ(SR[i].key,SR[j].key) TR[k]=SR[i++]; else TR[k]=SR[j++]; if(i<=m) for(l=0;l<=m-i;l++) TR[k+l]=SR[i+l]; /* 将剩余的SR[i..m]复制到TR */ if(j<=n) for(l=0;l<=n-j;l++) TR[k+l]=SR[j+l]; /* 将剩余的SR[j..n]复制到TR */ } int twopow(int i) //此处算2的幂 { int j=1; for(;i>0;i--) j*=2; return j; } void MergeSort(SqList *L) { /* 对顺序表L作归并排序。算法10.14 */ // MSort((*L).r,(*L).r,1,(*L).length); int i,j,k; SqList *L1=(SqList *)malloc(sizeof(SqList)); L1->length=N; for(i=1;i<=N;i++) L1->r[i]=L->r[i]; for(j=1;k=twopow(j-1),(L->length)/k>=1;j++) //确定归并的次数 { for(i=1;(i+k)<=L->length;i+=k*2) { if((i+k)==L->length||i+2*k-1>=L->length) { Merge(L->r,L1->r,i,i+k-1,L->length); continue; } Merge(L->r,L1->r,i,i+k-1,i+2*k-1); } for(i=1;i<=N;i++) L->r[i]=L1->r[i]; } free(L1); } void print(SqList L) { int i; for(i=1;i<=L.length;i++) printf("(%d,%d)",L.r[i].key,L.r[i].otherinfo); printf("\n"); } void main() { RedType d[N]={{49,1},{38,2},{97,3},{32,4},{76,5},{13,6},{12,7},{2,8},{3,9},{45,10}}; SqList l; int i,t; clock_t a,b; double c; loop: for(i=0;i<N;i++) l.r[i+1]=d[i]; l.length=N; printf("排序前:\n"); print(l); a=clock(); /*测试用时*/ //for(i=0;i<10000000;i++) for(i=0;i<10000000;i++) { for(t=0;t<N;t++) l.r[t+1]=d[t]; MergeSort(&l); } b=clock(); c=(double)(b-a)/1000; printf("用时为%f秒,%d,%d\n",c,a,b); printf("排序后:\n"); print(l); while(1) { printf("是否继续(y/n):"); if((t=getche(),printf("\n\n"),t)=='y') goto loop; if(t=='n') break; } }


下面就上面的代码,做一下彻底优化,把一些没必要的冗余计算,比如要算出具体的归并趟数,重复的赋值操作给去掉,得到相对高效的代码
/* alg10-10.c 归并排序(非递归版2) */ #pragma warning(disable: 4996) #include <stdio.h> #include <conio.h> #include <malloc.h> typedef int InfoType; /* 定义其它数据项的类型 */ #include "C10-1.h" #include "time.h" #define N 10 /* c9.h 对两个数值型关键字的比较约定为如下的宏定义 */ #define EQ(a,b) ((a)==(b)) #define LT(a,b) ((a)<(b)) #define LQ(a,b) ((a)<=(b)) void Merge(RedType SR[],RedType TR[],int i,int m,int n) { /* 将有序的SR[i..m]和SR[m+1..n]归并为有序的TR[i..n] 算法10.12 */ int j,k,l; /*int i0=i;*/ for(j=m+1,k=i;i<=m&&j<=n;++k) /* 将SR中记录由小到大地并入TR */ if LQ(SR[i].key,SR[j].key) TR[k]=SR[i++]; else TR[k]=SR[j++]; if(i<=m) for(l=0;l<=m-i;l++) TR[k+l]=SR[i+l]; /* 将剩余的SR[i..m]复制到TR */ //if(j<=n) // for(l=0;l<=n-j;l++) // TR[k+l]=SR[j+l]; /* 将剩余的SR[j..n]复制到TR */ /*for(l=i0;l<=j;l++) SR[l]=TR[l];*/ } void MergeSort(SqList *L) { int step = 1,i,right; int j; SqList *L1=(SqList *)malloc(sizeof(SqList)); L1->length=N; for(i=1;i<=N;i++) L1->r[i]=L->r[i]; while(step < N) { for(i = 1; i +step<= N; i += 2*step) { if(i+step-1 == N||i+2*step-1>=N) right = N; else right = i+step*2-1; Merge(L->r,L1->r , i, i+step-1, right); for(j=i;j<=right;j++) L->r[j]=L1->r[j]; } step *= 2; } free(L1); } void print(SqList L) { int i; for(i=1;i<=L.length;i++) printf("(%d,%d)",L.r[i].key,L.r[i].otherinfo); printf("\n"); } void main() { RedType d[N]={{49,1},{38,2},{97,3},{32,4},{76,5},{13,6},{12,7},{2,8},{3,9},{45,10}}; SqList l; int i,t; clock_t a,b; double c; loop: for(i=0;i<N;i++) l.r[i+1]=d[i]; l.length=N; printf("排序前:\n"); print(l); a=clock(); /*测试用时*/ for(i=0;i<10000000;i++) { for(t=0;t<N;t++) l.r[t+1]=d[t]; MergeSort(&l); } b=clock(); c=(double)(b-a)/1000; printf("用时为%f秒,%d,%d\n",c,a,b); printf("排序后:\n"); print(l); while(1) { printf("是否继续(y/n):"); if((t=getche(),printf("\n\n"),t)=='y') goto loop; if(t=='n') break; } }
测试结果如下:
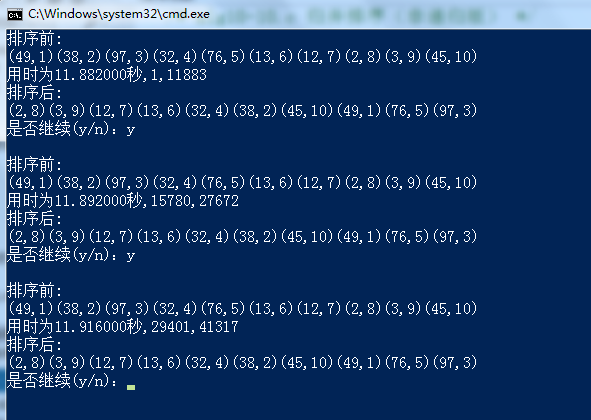

显然,Debug版本的效率要比递归版本的要快,但Release版本优化后的效率还是没有递归版的优化效果好。显然在某些时候,递归形式的写法,虽然理解上费劲,(其实数学归纳法学的好,写正确的递归代码并非难事),实用性较差,很多人为了代码的可读性,都不建议写递归形式,虽然形式上简洁。甚至在一般情况下,递归的写法,会因为频繁的入栈出栈而损耗效率。可是事实也许并非如此,编译器对递归函数的优化,有时候明显要比一般的非递归算法要强。




