HDMI/DVI____TMDS编码
一.编码步骤:

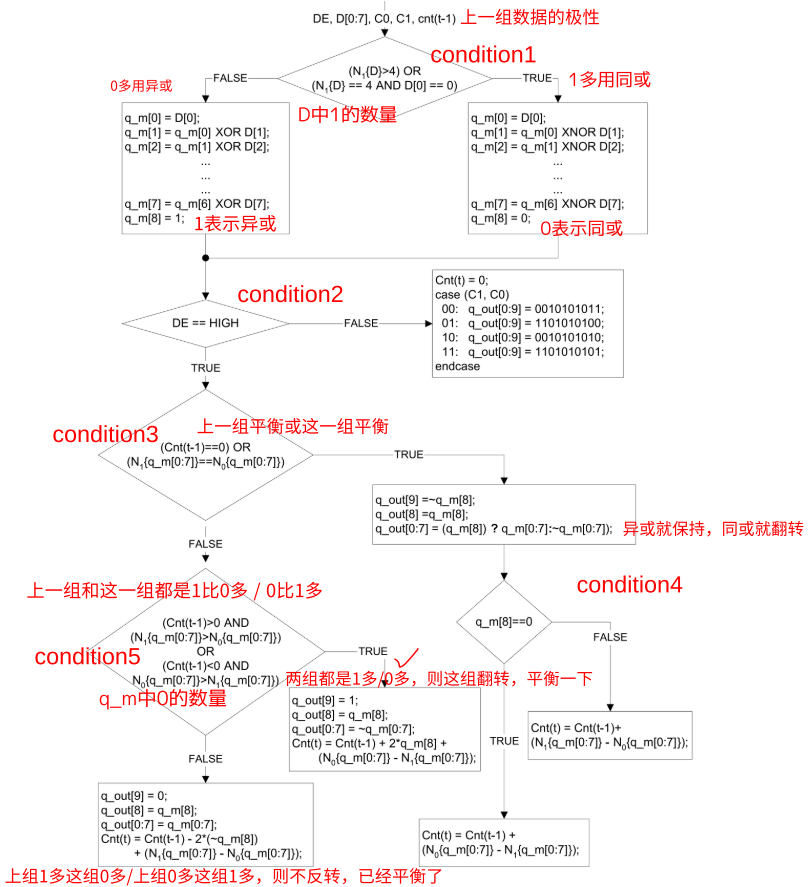
基本方法:取第一位数据为初值,接下来输入的每一位与前一导出的位(根据判断条件)进行异或XOR或者同或XNOR(最小化传输,减少0/1翻转);最后选择性反转这9bit数据(DC平衡处理,平衡0和1的个数)。
①DE为高电平时,对8位RGB数据编码,第9bit表示采用了XOR / XNOR ,第10bit表示是否翻转。
②DE为低电平时,根据2bit的控制位(4种情况)输出10bit数据(固定4个值)。(直接使用查找表)。
知识点:一组数据中0的个数多,用异或可减少翻转次数
一组数据中1的个数多,用同或可减少翻转次数
例子如下:

二.编码流程:
三.代码设计
抛开流程图设计思想,只看图设计代码,这种类型的代码编码一般有一下流程:
①.先把输入的数据用寄存器打x拍,实现流水线对齐。
②.单独拎出所有三角形,用组合逻辑语句设计判决条件:
condition1 = ( 三角形内部语句 ) ? 1 : 0 ;
同理......
③.用时序逻辑按顺序根据条件编写输出。
//根据流程图写代码 //啥时候用组合啥时候用时序?判决条件用组合,打拍,输出用时序。输入经过打拍之后,后面其实可以根据需要使用组合逻辑 module TMDS_coder ( input clk , input resetn , input d_e , input [7:0]d_in , input c0 , input c1 , output reg[9:0]d_out ); reg [4:0]cnt ;//极性寄存器,计数器差距统计:统计 1 和 0 是否过量发送,最高位(cnt[4])是符号位 reg [7:0]d_in_reg ;//输入数据寄存器 wire [8:0]d_m ;//9bit寄存器 reg [3:0]numd1 ;//计数8bit中1的个数 reg [3:0]numd0 ;//计数8bit中0的个数 reg [3:0]numd_m1 ;//计数8bit中1的个数 reg [3:0]numd_m0 ;//计数8bit中0的个数 //控制信号输出查找表 parameter c1c0_00 = 10'b1101010100; parameter c1c0_01 = 10'b0010101011; parameter c1c0_10 = 10'b0101010100; parameter c1c0_11 = 10'b1010101011; //输入数据打一拍,统计输入的数据0和1的个数 always@(posedge clk) begin d_in_reg <= d_in ; numd1 <= d_in_reg[0] + d_in_reg[1] + d_in_reg[2] + d_in_reg[3] + d_in_reg[4] + d_in_reg[5] + d_in_reg[6] + d_in_reg[7] ; numd0 = 'd8 - ( d_in_reg[0] + d_in_reg[1] + d_in_reg[2] + d_in_reg[3] + d_in_reg[4] + d_in_reg[5] + d_in_reg[6] + d_in_reg[7] ) ; end //判定条件设计: //知识点(经验):把流程图的判定条件用组合逻辑定义成一个变量(是/否 --> 1/0 ) (之前显示屏取范围亦是如此) //状态机用的是时序逻辑,区别 wire condition1 ;//条件1 assign condition1 = (numd1 > 4 ) || ( (numd1 == 4 ) && ( d_in[0] == 0 ) ) ; //这里用了组合逻辑赋值 assign d_m[0] = d_in_reg[0] ; assign d_m[1] = (condition1) ? ~( d_m[0]^d_in_reg[1] ) : ( d_m[0]^d_in_reg[1] ) ; assign d_m[2] = (condition1) ? ~( d_m[1]^d_in_reg[2] ) : ( d_m[1]^d_in_reg[2] ) ; assign d_m[3] = (condition1) ? ~( d_m[2]^d_in_reg[3] ) : ( d_m[2]^d_in_reg[3] ) ; assign d_m[4] = (condition1) ? ~( d_m[3]^d_in_reg[4] ) : ( d_m[3]^d_in_reg[4] ) ; assign d_m[5] = (condition1) ? ~( d_m[4]^d_in_reg[5] ) : ( d_m[4]^d_in_reg[5] ) ; assign d_m[6] = (condition1) ? ~( d_m[5]^d_in_reg[6] ) : ( d_m[5]^d_in_reg[6] ) ; assign d_m[7] = (condition1) ? ~( d_m[6]^d_in_reg[7] ) : ( d_m[6]^d_in_reg[7] ) ; assign d_m[8] = (condition1) ? 0 : 1 ; //统计9bit寄存器中数据位0/1个数 always@(posedge clk) begin numd_m1 = d_m[0] + d_m[1] + d_m[2] + d_m[3] + d_m[4] + d_m[5] + d_m[6] + d_m[7] ; numd_m0 = 'd8 - ( d_m[0] + d_m[1] + d_m[2] + d_m[3] + d_m[4] + d_m[5] + d_m[6] + d_m[7] ) ; end wire condition2 ;//条件2 assign condition2 = d_e ; wire condition3 ;//条件3 assign condition3 = ( (cnt == 0 ) || ( (numd_m1) == ( numd_m0) ) ) ; wire condition4 ; assign condition4 = (d_m[8] == 0) ? 1 : 0 ; wire condition5 ;//大于零小于零的问题怎么解决?教程用符号位解决,不知道cnt是怎么能算出来的。 assign condition5 = ( ((~cnt[4]) && (numd_m1 > numd_m0) ) || ( (cnt[4] ) && ( numd_m0 > numd_m1 ))) ; /*如何统计1/0个数的多/少了几个,是设计角度的问题。为了D/C平衡(直流均衡),才做统计,流程处理,如果不做均衡可以不处理。 从代码的角度看,只需要知道cnt[4]是符号位就可以判断了。 */ /*怎么样设计关联多次输入的变量cnt啊? 想法:设计一个输入一个输出,输出接到输入... 教程方法:本来就能存cnt值,只要不去刷新他 */ reg [1:0]c0_reg ; reg [1:0]c1_reg ; reg [1:0]d_e_reg ; reg [8:0]d_m_reg ; //流水线对齐,打2拍,d_m输入时已经打一拍了,这里打一拍 always@(posedge clk) begin c0_reg <= {c0_reg[0],c0}; c1_reg <= {c1_reg[0],c1}; d_e_reg <= {d_e_reg[0] , d_e } ; d_m_reg <= d_m ; end //设计输出 always@(posedge clk or negedge resetn ) if(!resetn) begin cnt <= 0 ; d_out <= 0 ; end else begin if ( condition2 ) begin if (condition3) begin d_out[9] <= ~d_m_reg[8] ; d_out[8] <= d_m_reg[8] ; d_out[7:0] <= (d_m_reg[8]) ? d_m_reg[7:0] : ~d_m_reg[7:0] ; if(condition4) begin cnt <= cnt + ( numd_m0 - numd_m1 ) ; end else begin cnt <= cnt + ( numd_m1 - numd_m0 ) ; end end else begin if(condition5) begin d_out[9] <= 1 ; d_out[8] <= d_m_reg[8] ; d_out[7:0] <= ~d_m_reg[7:0] ; cnt <= cnt + ( d_m_reg[8] << 1 ) + ( numd_m0 - numd_m1 ) ; end else begin d_out[9] <= 0 ; d_out[8] <= d_m_reg[8] ; d_out[7:0] <= d_m_reg[7:0] ; cnt <= cnt - ( d_m_reg[8] << 1 ) + ( numd_m1 - numd_m0 ) ; end end end else begin cnt <= 0 ; case({c1_reg[0],c0_reg[0]}) 2'b00 : d_out <= c1c0_00 ; 2'b01 : d_out <= c1c0_01 ; 2'b10 : d_out <= c1c0_10 ; 2'b11 : d_out <= c1c0_11 ; endcase end end endmodule
仿真结果:



 浙公网安备 33010602011771号
浙公网安备 33010602011771号