KMP算法学习

参考： https://www.zhihu.com/question/21923021

1.kmp

字符串m,需要查询存在m中的字符串p

m长度为 len1 p长度len2

解决方法

1.暴力法

直接遍历m，判断p中的第一个字母是否相同，然后继续往后判断，如果失败，继续从当前字符开始，遍历p，判断是否相同，时间复杂度需要O(m*n)

2.Kmp法

• KMP算法的核心，是一个被称为部分匹配表(Partial Match Table)的数组

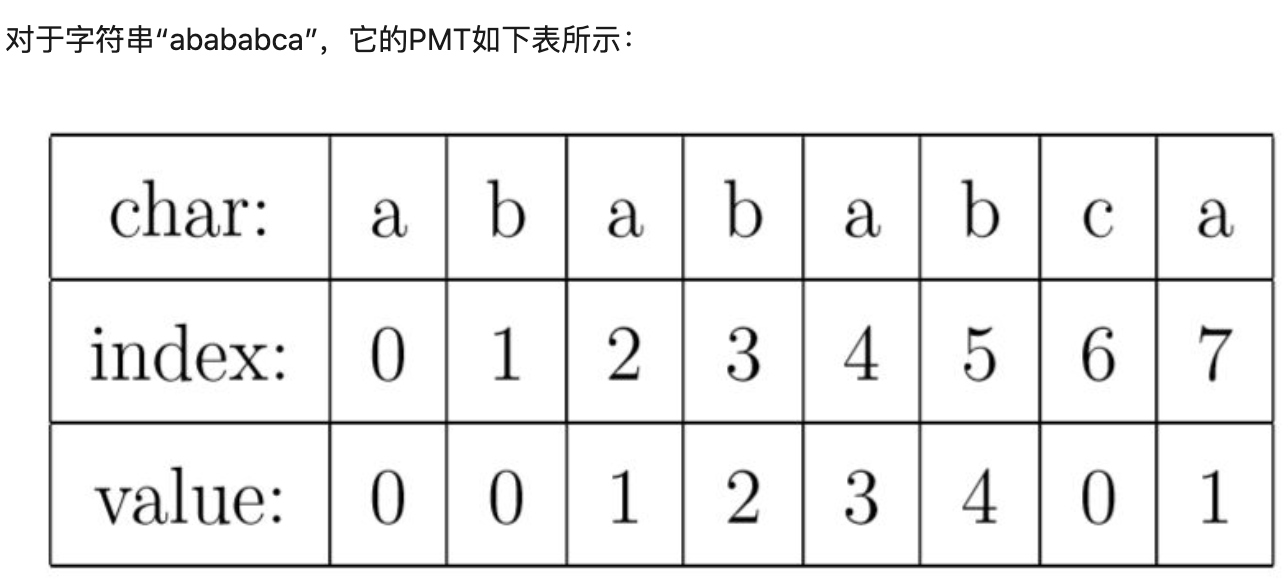
• 前缀与后缀

如果字符串A=sb,则称s为字符串A的前缀，b为A的后缀。要注意的是，字符串本身并不是自己的后缀

PMT中的值是字符串的前缀集合与后缀集合的交集中最长元素的长度

• 这个最长前后缀元素表示含义：

如果当前字符串为ababab，记为S1,长度为Slen,则

前缀：{a,ab,aba,abab,ababa}

后缀：{b,ba,bab,abab,babab}

交集最长元素为：abab,记为C1 ，该长度为4

该长度的意义是什么？

参考暴力法可知：当匹配失败的时候，我们需要从字符串开头开始比对，但是C1可以代表从0开始到长度4，即[0,4)不用匹配，因为本身他与从S1的[slen-1-4,slen-1]相等。

所以对于字符串m，p来说，当匹配到m[i]、p[j]处，如果m[i]!=p[j],则p应该从p[PMT[j-1]]处开始匹配，对于p[0-PMT[j-1])字符子串来说，已经算是匹配过了。

KMP实际对比流程

• 创建PMT表，计算出每个字符对应的PMT值，第一个字符为0
• i，j从0开始：当m遍历到i，p遍历到j时(j>0),此时 m[i]==p[j] 可知从p[0,j]与m[i-j-1,i]相等，继续向后遍历
• 如果m[i+1]!=p[j+1],此时我们知道对于p[0,j]==m[i-j-1,i]相等，因此可以通过pmt[j]=k,快速从p[0]处跳到p[k]处进行匹配。

next

对于PMT表我们通常使用next表来进行表示，对于PMT表来说，每次计算需要考虑PMT[j-1],所以next数组为了计算方便，将PMT数组整体向右移动一位，则每次计算只考虑next[j]即可。 计算方式如下：

//使用p的前缀匹配p
static int[] generate(String p){
		int[] next=new int[p.length()];
		//从-1开始，前缀，从0开始匹配，后缀
		int j=-1,int i=0;
		while(i<p.length()-1){
			if(j==-1 || p.charAt(i)==p.charAt(j)){
			  //相等（符合前后缀公共子串）即更新PMT值，或者第一次，直接赋值为0
				i++;
				j++;
				next[i]=j;
			}else{
			  //无法匹配，继续寻找前一个可以匹配位置。
				j=next[j];
			}
		}
		return next;
}

KMP

    String a="helloabacs123",p="abac";
		int[] next = generate(p);
		int j=0,i=0;
		while(i<a.length() && j<p.length()){
			if(j==-1 || a.charAt(i)==p.charAt(j)){
				j++;
				i++;
			}else{
				j= next[j];
			}
		}
		if(j>=p.length()) System.out.println(i-j);
		System.out.println(-1);