【淘汰9成NLP工程师的常识题】LSTM的前向计算如何进行加速？
【淘汰9成NLP工程师的常识题】LSTM的前向计算如何进行加速？
重要性：★★★ 💯
这是我常用的一个面试题。看似简单的基础题，但在面试中能准确回答的不足10% ，常识题的错误反而会让人印象深刻。
此题的关键主要是考察面试者对大矩阵运算和MapRrduce思想的理解。
NLP Github 项目：
-
NLP 项目实践：fasterai/nlp-project-practice
介绍：该仓库围绕着 NLP 任务模型的设计、训练、优化、部署和应用，分享大模型算法工程师的日常工作和实战经验
-
AI 藏经阁：https://gitee.com/fasterai/ai-e-book
介绍：该仓库主要分享了数百本 AI 领域电子书
-
AI 算法面经：fasterai/nlp-interview-handbook#面经
介绍：该仓库一网打尽互联网大厂NLP算法面经，算法求职必备神器
-
NLP 剑指Offer：https://gitee.com/fasterai/nlp-interview-handbook
介绍：该仓库汇总了 NLP 算法工程师高频面题
核心思想：将小矩阵合并成大矩阵再进行梯度分块（Reduce → Map）。
- 合并计算遗忘门、输入门、输出门和新增信息的仿射变换，使用“大矩阵”加速运算
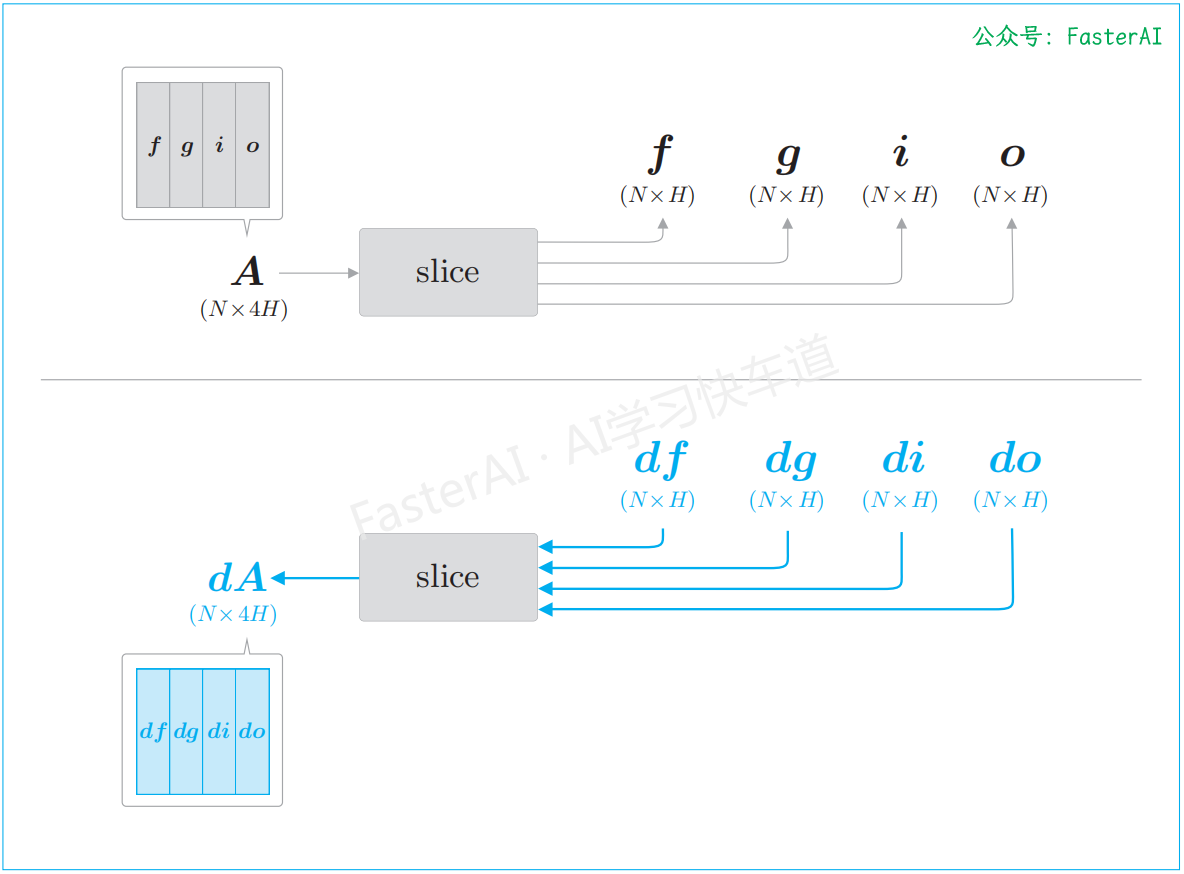
- 通过slice 节点将矩阵分成了 4 份，因此它的反向传播需要整合 4 个梯度
现在我们先来整理一下 LSTM 中进行的计算，如下所示：
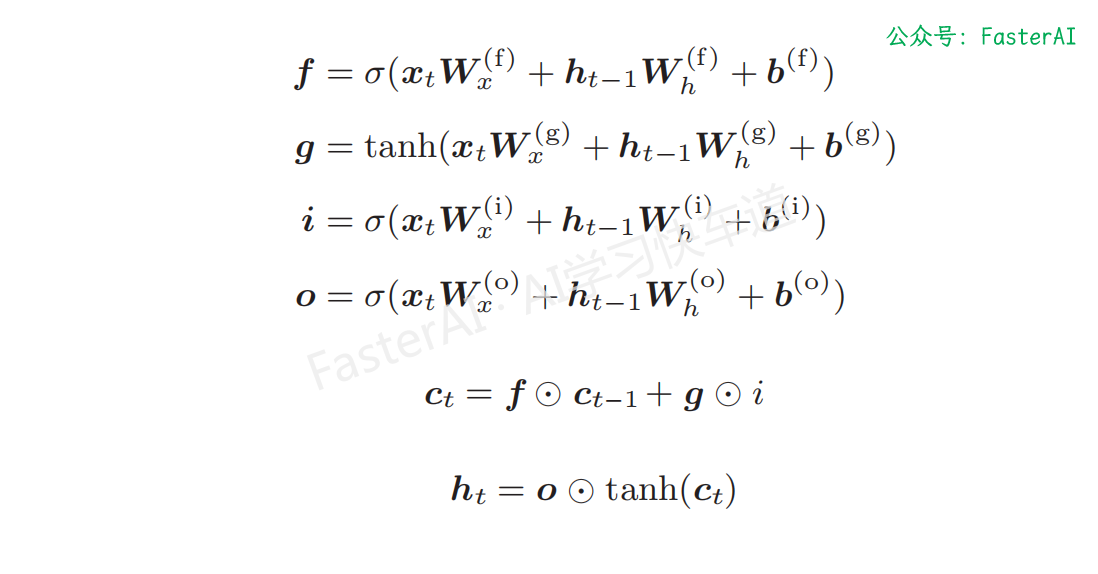
这里需要注意式中的 4 个仿射变换。这里的仿射变换是指 $xW_x + hW_h + b$ 这样的式子。4 个仿射变换，其实可以整合为通过 1 个式子进行，如下图所示。
整合4个权重，通过1次仿射变换进行4个计算：
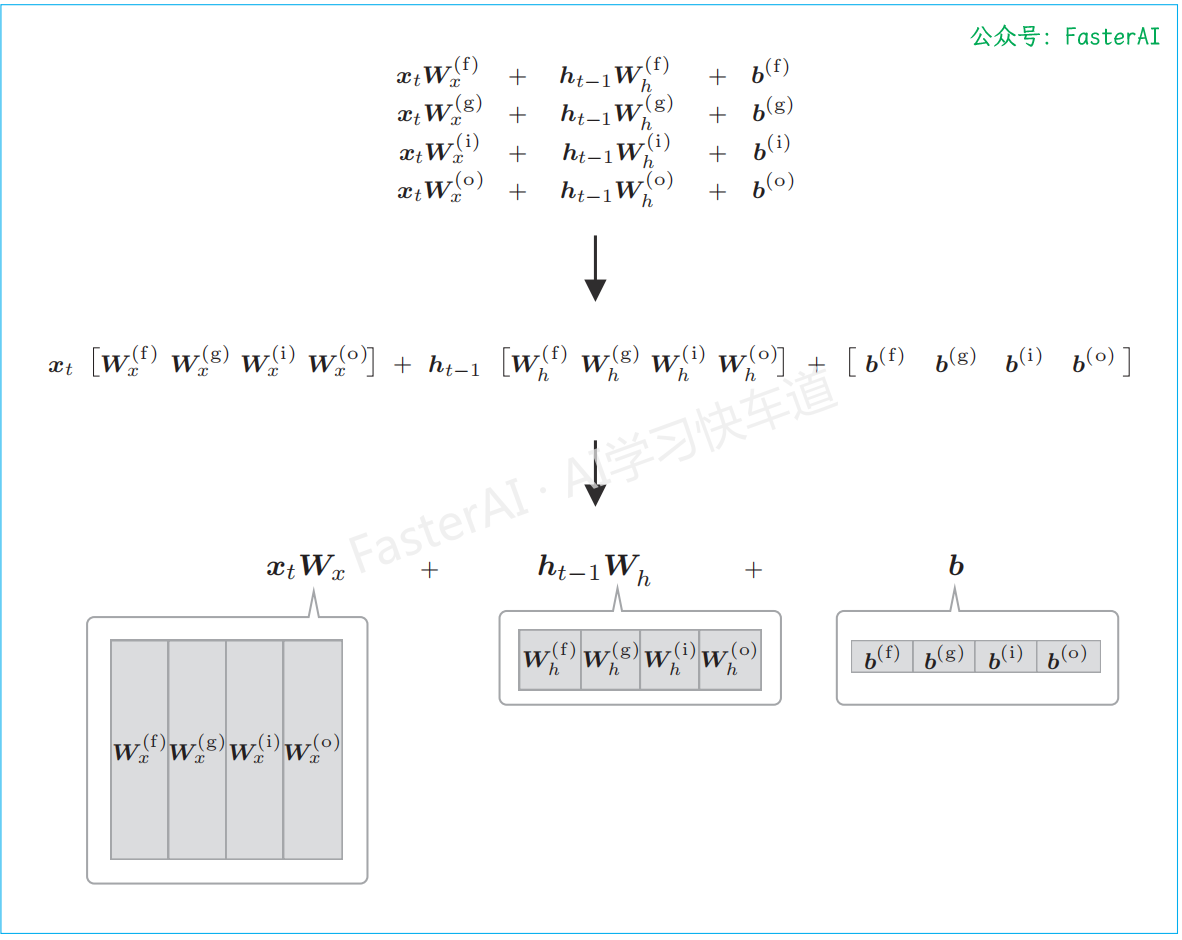
如此，原本单独执行 4 次的仿射变换通过 1 次计算即可完成，可以加快计算速度。这是因为矩阵库计算“大矩阵”时通常会更快。
整合4个权重进行仿射变换的LSTM的计算图：
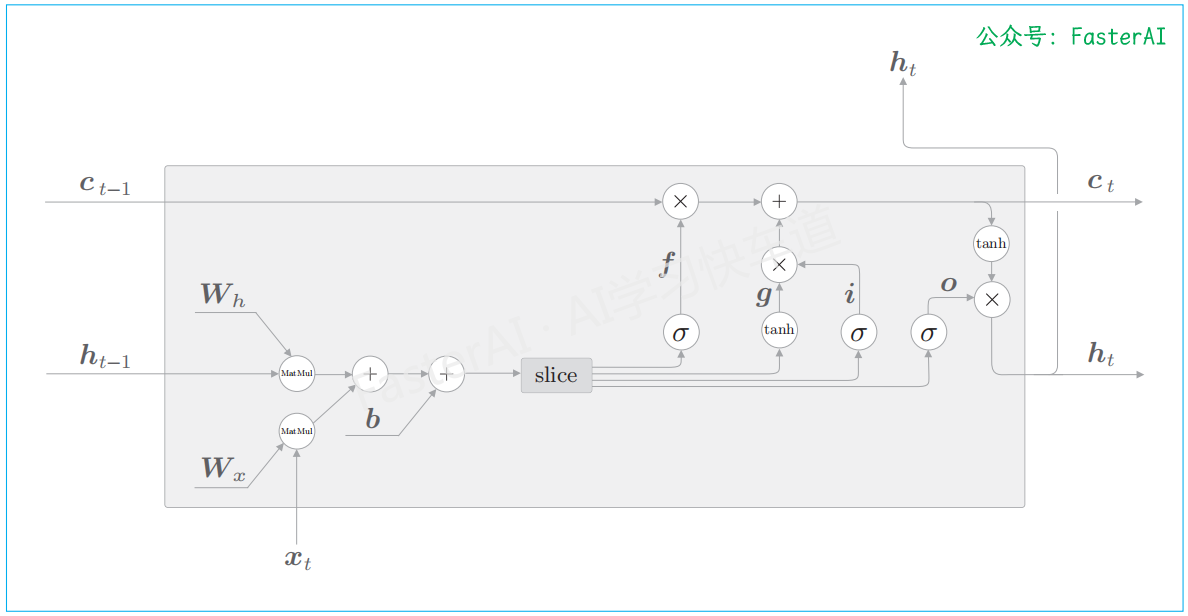
仿射变换的形状的改变：
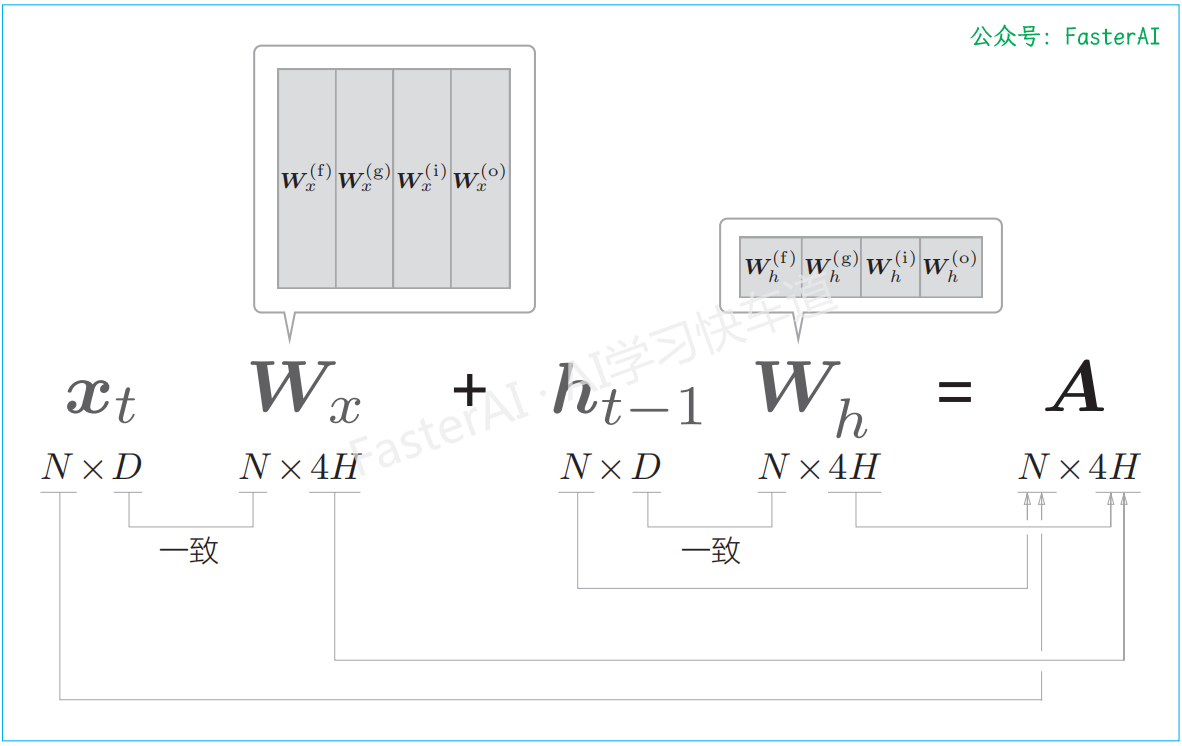
批大小是 N，输入数据的维数是 D，记忆单元和隐藏状态的维数都是 H。另外，计算结果 A 中保存了 4 个仿射变换的结果。因此，通过 A[:, :H]、A[:, H:2H] 这样的切片取出数据，并分配给之后的运算节点。
slice节点的正向传播（上）和反向传播（下）：
本文由mdnice多平台发布
