Federated Learning with Matched Averaging

本文提出了联邦匹配平均（FedMA）算法。FedMA通过对提取到的具有相似特征的隐元素（即卷积层的通道，LSTM的隐状态，全连接层的神经元）进行匹配和平均，按层构建共享全局模型。FedMA训练的CNN和LSTM模型在数据集MNIST,CIFAR-10,Shakespeare上优于最新联邦学习算法FedProx，同时提高了通信效率。

按我的理解，由于模型可辨识性（model identifiability）问题，神经网络和任意具有多个等

效参数化潜变量的模型都会具有多个局部极小值。如果一个足够大的训练集可以唯一确定一组模型参数，那么该模型被称为可辨认的。带有潜变量的模型通常是不可辨认的，因为通过相互交换潜变量我们能得到等价的模型。例如，考虑神经网络的第一层，我们可以交换单元 i 和单元 j 的传入权重向量、传出权重向量而得到等价的模型。如果神经网络有 m 层，每层有 n 个单元，那么会有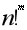种排列隐藏单元的方式。这种不可辨认性被称为权重空间对称性（weight space symmetry）。根据这种对称性任何给定的神经网络，它的许多变化只在参数的顺序上不同，构成了实际等价的局部最优。概率联邦神经匹配（PFNM）通过在对神经网络的参数求平均值之前找到其参数的排列来解决这个问题。本文在PFNM的基础上提出了FedMA算法。

本文讨论了为什么FedAvg中对所有客户端的模型参数直接平均是不合理的，例如：在最简单的单隐藏层全连接神经网络中，FC神经网络可以表示为：

根据对称性可以写为：

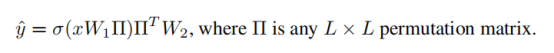
L是隐含层的节点数目，置换矩阵∏将W1的L列与W2的L行进行置换。

假设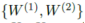是最佳权重，在同质数据集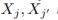上训练的权重为

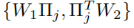
找不到任何置换矩阵使得

成立

所以不能在一开始就做

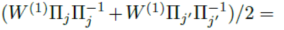
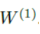
（即两个模型参数直接平均就可以得到最优模型）

联邦匹配平均优化公式：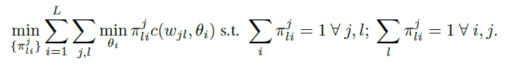

 

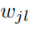 表示从数据集j中学习得到的第l个神经元表示全局模型中的第i个神经元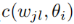，是这一对神经元的相似函数

 

给定J个客户端提供的权重计算得到联邦神经网络权重：

 

 

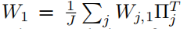
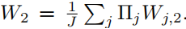
基于优化公式与最大二分匹配问题的关系，所以本文将此方法称为匹配平均。

在每次迭代中，先根据给定的权值矩阵估计找到对应的全局模型，然后根据匈牙利算法将全局模型和数据集j'上的局部神经元进行匹配，得到新的拓展全局模型，由于数据异质性，局部模型j'可能存在部分神经元，它们不存在于由其他局部模型构成的全局模型中。因此，我们希望避免“差”匹配，即如果最优匹配的代价大于某个阈值，从相应的局部神经元创建一个新的全局神经元。还需要一个中等大小的全局模型，因此用一些递增函数f(L')来惩罚它的大小。其中，全局模型大小记为L。

FedMA算法：

首先，中央服务器只从客户端收集第一层的权重，并执行前面描述的单层匹配以获得联邦模型的第一层权重。然后中央服务器将这些权重广播给客户端，客户端继续训练其数据集上的所有连续层，同时保持已经匹配的联邦层冻结。然后，将此过程重复到最后一层，根据每个客户端数据的类比例对其进行加权平均。FedMA 方法要求通信轮数等于网络中的层数。

 

实验分析 

数据集：MNIST,CIFAR-10,Shakespeare

模型：VGG-9,LSTM

下图展示了层匹配 FedMA 在更深的 VGG-9和 LSTM 上的性能。在异构环境中，FedMA 优于 FedAvg、FedProx和其他基线模型（即客户端 CNN模型及其集成）训练得到的 FedProx。

 

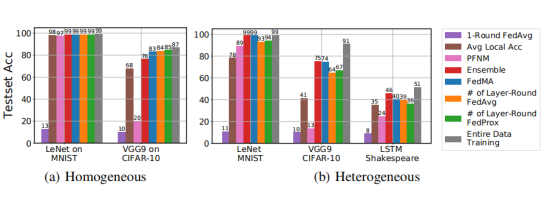
FedMA 的优点之一是它比 FedAvg 更有效地利用了通信轮次，即 FedMA 不是直接按元素平均权重，而是识别匹配的卷积滤波器组，然后将它们平均到全局卷积滤波器中。

最后，作者研究了 FedMA 的通信性能。通过将 FedMA 与 FedAvg、FedProx 进行比较，FedMA 在所有情况下都优于 FedAvg 和 FedProx。

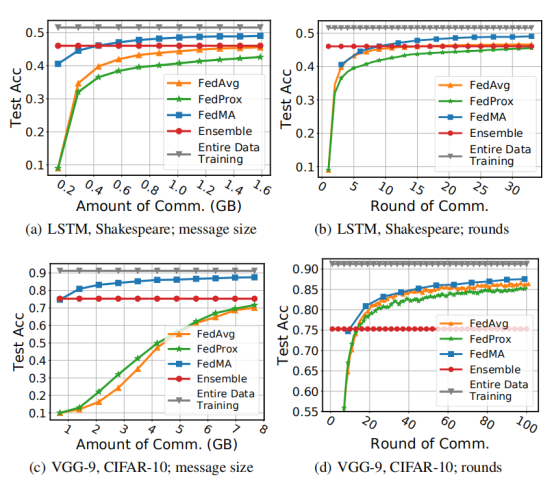
总结：

本文提出了一种利用概率匹配和模型大小自适应的分层联邦学习算法FedMA，通过实验验证了FedMA的收敛速度和通信效率。本文证明了 FedMA 可以有效地利用训练后的局部模型。在后续工作中，作者考虑利用近似二次分配解（Approximate Quadratic Assignment Solutions）的方法引入其他的神经网络层，例如残差连接和批量归一化层，从而进一步改进LSTM的联邦学习效果。此外，探索 FedMA 的容错性并研究其在更大数据集上的性能非常重要，特别是针对那些即使在数据可以聚合的情况下也无法进行有效训练的数据集。