二分求幂/快速幂取模运算——root(N,k)

二分求幂

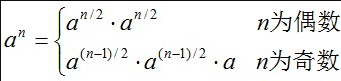
int getMi(int a,int b)
{
    int ans = 1;
    while (b != 0)
    {
        //当二进制位k位为1时，需要累乘a的2^k次方，然后用ans保存
        if (b % 2 == 1)
        {
            ans *= a;
        }
        a *= a;
        b /= 2;
    }
    return ans;
}

快速幂取模运算

公式：

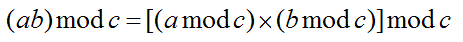
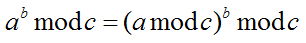
最终版算法：

int PowerMod(int a, int b, int c)  
{  
　　int ans = 1;  
　　a = a % c;  
　　while(b>0)  
　　{  
　　　　if(b % 2 = = 1)ans = (ans * a) % c;  
　　　　b = b/2;  
　　　　a = (a * a) % c;  
　　}  
　　return ans;  
}  

求Root(N,k)

题目描述

       N<k时，root(N,k) = N，否则，root(N,k) = root(N',k)。N'为N的k进制表示的各位数字之和。输入x,y,k，输出root(x^y,k)的值 (这里^为乘方，不是异或)，2=<k<=16，0<x,y<2000000000，有一半的测试点里 x^y 会溢出int的范围(>=2000000000) 

输入描述

      每组测试数据包括一行，x(0<x<2000000000), y(0<y<2000000000), k(2<=k<=16)

输出描述    

 输入可能有多组数据，对于每一组数据，root(x^y, k)的值
输入

4 4 10
输出

4

 代码：

#include <cstdio>
#include <math.h>
#include <cstring>
#include <algorithm>

//root(x*y,k) = root(root(x,k)*root(y,k),k)

int Root(int N,int k)
{
    if(N<k)return N;
    int ans = 0;
    //N大于k， 求N为k进制时各位之和
    while(N != 0){
        ans += N%k;
        N /= k;
    }
    return Root(ans,k);
}

int getAns(int x,int y,int k)
{
    int num = Root(x,k);
    int ans = 1;
    while(y > 0){
        if(y%2){//y为奇数
            ans = Root(ans*num, k);
        }
        y /= 2;
        num = Root(num*num, k);
    }
    return ans;
}


int main()
{
    int x,y,k;

    while(~scanf("%d %d %d",&x,&y,&k)){
        printf("%d\n",getAns(x,y,k));

    }

    return 0;
}