软件工程第三次作业（最大子段和）

最大连续子数组和（最大子段和）

本项目托管在coding上：传送门

1. 问题

给定n个整数（可能为负数）组成的序列a1,a2,a[3],…,a[n],求该序列如a[i]+a[i+1]+…+a[j]的子段和的最大值。当所给的整数均为负数时定义子段和为0，依此定义，所求的最优值为： Max{0,a[i]+a[i+1]+…+a[j]},1<=i<=j<=n
例如，当（a[1],a[2],a[3],a[4],a[5],a[6]）=(-2,11,-4,13,-5,-2)时，最大子段和为20。
-- 引用自《百度百科》

2. 分析

这是一个经典问题，容易想到一种时空复杂度为 O(n) 做法：

遍历一遍，一边遍历一边维护一个连续子段的和sm，如果sm加上当前的遍历值小于等于0，则说明前面的子段对于后面的子段不再有正贡献，则可以舍弃前面的子段，sm值置为0，继续遍历。在这个过程中不断更新sm的最大值mx。
这个过程可以被简单表示为：

for i = 1 to n : $$sm = \begin{cases} 0, & \text {if \(sm+aa[i]\) <= 0} \sm+aa[i], & \text{if \(sm+aa[i]\) >0} \end{cases}$$ ,mx = max(mx,sm）

很显然，这个动态规划的过程是正确的。

3. 设计

Sometimes you can see a problem in a different way, and rewrite it so that a special case goes away and becomes a normal case. And that's good code.
——Linus Torvalds

这段引用有点班门弄斧。我只是不想看起来在应付了事，而是经过认真的思考才决定写下下面这种精简的代码，理由如下：

• 测试是为了验证程序的正确性，覆盖程度越高越好。但是不能为了让测试有更加直观的高级别覆盖，而故意增加代码的分支跟条件。这样就失去本来的目的了。比如，系统函数max(a,b)（只要能够胜任需要的功能），可以保证较高的效率，也能将测试变的简单，你只需要关心这个函数的接口就可以了。一般没有改写成形如 (a>b)?a:b 这种代码的必要性。

• 对于一个软件来说，如果代码分支在设计上可以做到更少，则就能够更轻易在可能的扩展中的达到更高级别的覆盖。

• 如果对于每个判定，条件只有一个，在这个情况下 判定覆盖 = 条件覆盖 = 判定/条件覆盖 = 条件组合覆盖，如果能做到这样，我们没有必要为了让各种覆盖看起来不一样，而选择更加复杂的逻辑。

（参考资料：《软件测试的艺术》The Art of Software Testing）

在这种想法的指导下，我的程序流程如下：

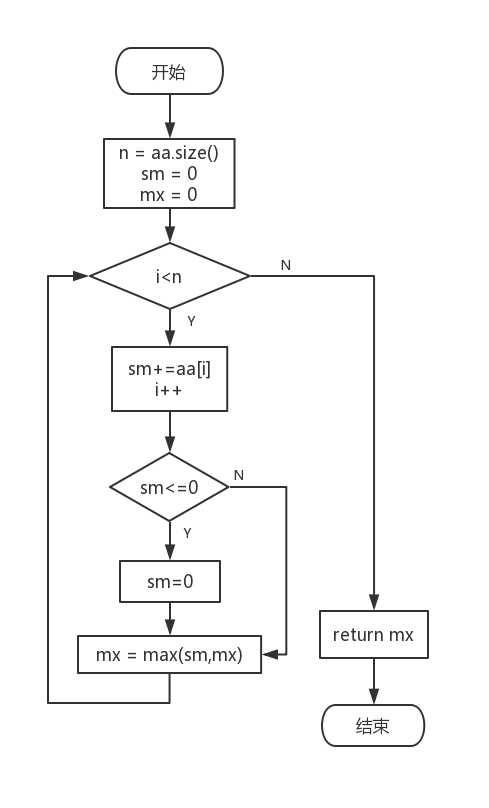
代码如下：

int InterSum(vector<int> &aa)
{
	int n = aa.size();
	int sm = 0, mx = 0;
	for (int i = 0; i < n; ++i) {
		sm += aa[i];
		if (sm <= 0) sm = 0;
		mx = max(sm, mx);
	}
	return mx;
}

4. 测试
白盒测试达到了 条件组合覆盖 ，测试用例如下：

namespace UnitTest1
{		
	TEST_CLASS(UnitTest1)
	{
	public:
		
		TEST_METHOD(NormalCase1)
		{
			std::vector<int> vec = {1,2,-4,2,6,-5,9};
			Assert::AreEqual(InterSum(vec),12);
		}
		TEST_METHOD(NormalCase2)
		{
			std::vector<int> vec = { -7,1,100,2,-101,99,21,0,32,-1 };//55+99=154
			Assert::AreEqual(InterSum(vec), 154);
		}
		TEST_METHOD(AllNegi)
		{
			std::vector<int> vec = { -1,-3,-7,-111 };
			Assert::AreEqual(InterSum(vec), 0);
		}
		TEST_METHOD(AllZero)
		{
			std::vector<int> vec(5,0);
			Assert::AreEqual(InterSum(vec), 0);
		}
		TEST_METHOD(Empty)
		{
			std::vector<int> vec(0);
			Assert::AreEqual(InterSum(vec), 0);
		}
	};
}

测试结果：

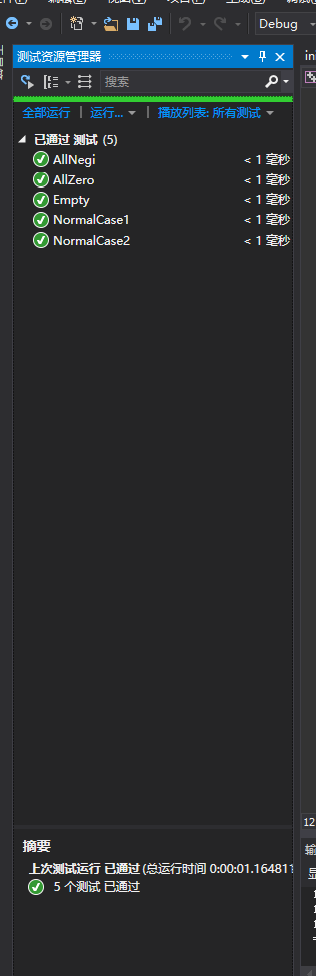
PEACE!