【论文笔记】SNIP:An Analysis of Scale Invariance in Object Detection
&论文概述
论文题目:An Analysis of Scale Invariance in Object Detection–SNIP
作者&出处:Bharat Singh,Larry S.Davis || University of Marvland. College Park
获取地址:https://arxiv.org/pdf/1711.08189.pdf
&总结与个人观点
通过对极限尺度(太大或太小)多样性下的识别与检测目标的不同技巧的分析,引出当前目标检测训练管道的缺点。提出SNIP以解决参与训练的较宽尺度的目标实例以及减少预训练分类网络的domain shift。在COCO数据集上的实验体现了目标检测中的尺度以及图像金字塔的重要性。因为不需要对高分辨率图像中的大目标进行梯度后向传播,可能减少图像中相当大的部分的计算量。
SNIP相当于在图像金字塔中的每一层设定了固定的范围,只有满足该范围的anchor或者IoU满足一定范围才能进行下一步。
&贡献
1) 使用详尽的实验来验证分辨率、尺度、数据多样性以及域偏移对整个检测结构的性能的影响;
2) 提出SNIP对多尺度训练进行改进,在每种分辨率中只有符合相应条件的anchor才会被选中,既保存了面部与姿势的多样性,又能将需要的结果统一化到需要的尺度中。
&拟解决的问题
问题:在目标实例中较大的尺度变化,尤其是检测非常小的目标是影响性能的因素之一
分析:相对于ImageNet(分类)与COCO数据集中的图片的中间尺度由下图可知,分别是0.106与0.556。其中纵轴CDF表示累计分布函数,到当前相对尺度为止的所有占比。
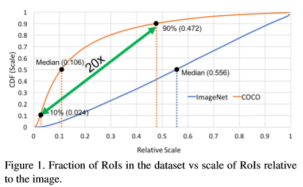
- 也就是说COCO数据集中大多数的目标实例均小于图片区域的1%;
- 且10%与90%的尺度占比分别为0.024与0.472,即尺度的变化相差了20倍左右,这个尺度范围很大而且对CNN中尺度不变性造成了冲击;
- 在分类与检测数据集中目标实例的尺度不一致也导致了在对预训练的分类网络的精调时的domain-shift。
为了解决由尺度多样性以及小目标实例引起的问题,提出了很多方法,如将浅层特征与深层特征结合来检测小目标、使用空洞/可变形卷积来增强感受野以识别大目标、在不同分辨率的层级中的独立预测以捕获不同尺度的目标实例、使用上下文消除歧义、多尺度训练或测试、预测时结合NMS等。即便这些方法改进了目标检测的性能,但仍有一些重要的问题没有处理:
- 通过上采样来获得更好的检测性能是否必要?在检测数据集中典型的图片size为480×640,为什么要将其上采样到800×1200?是否能够在ImageNet中的低分辨率图像中预训练更小的strides的CNNs,之后再检测数据集中精调以检测小目标实例?
- 当对预训练的图像分类模型进行精调时,训练目标实例的分辨率在rescale输入图像后是否应当限制在窄的范围(64×64到256×256)?或者对输入图像的所有上采样目标分辨率(从16×16到800×1000)应当参与到训练中?

对于特征金字塔来说,如果目标的size为25×25,即便在训练时使用stride为2的上采样,也只能将其扩展到50×50,而预训练的网络一般在图像分辨率为224×224进行训练。因此,即便是通过特征金字塔生成的高层级语义特征对小目标分类也没有用处。故将其与浅层特征结合对检测小目标也没有作用。即便特征金字塔利用了网络中所有层级的特征,在检测小/大目标时也不会优于图像金字塔。
&框架及主要研究方法
1、domain shift的影响:
在训练和测试中输入不同分辨率的图像引起的域偏移。提出对该问题的分析主要是因为当前最优的检测器使用800×1200的分辨率进行训练,而推断时却在图像金字塔上进行,包括更高的分辨率1400×2000以检测小目标。
实验1:通过对原始的ImageNet数据集中的图像进行下采样获得48×48,64×64,80×80,96×96以及128×128的图像,然后将其上采样到224×224作为在224×224图像上训练的CNN结构的输入(CNN-B)。下图为其对应的top-1精度:
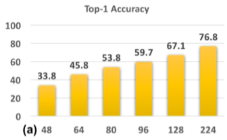
从中可以看出当训练与测试的图片在分辨率上的差距增大时,性能上也会出现相应的下降。因此,至少对于图像分类来说,使用没有训练过的对应分辨率的图像进行测试时,结果不会达到最优。
实验2:通过实验1的结论可知,在ImageNet上预训练使用不同的stride的网络有助于提高检测精度。对48×48的图像使用stride=1,3×3卷积核放在ResNet-101的第一层进行训练(CNN-S),同样的对96×96的图像,使用stride=2,5×5卷积。此外使用标准的数据增强方法,如随机裁取、色彩增强等。对应的结果如下:


可见对地分辨图像使用不同结构的分类网络继续预训练对低分辨率目标的识别精度增强有效。
实验3:同样,通过实验1,在对上采样的低分辨率图像上对CNN-B进行精调也利于小目标检测(CNN-B-FT)。结果参见实验2的对比图。
实验结果表明,在高分辨率图像上学到的filter对识别低分辨率图像仍然有效。因此,相比于使用strde为2的下采样,将图像上采样2次,之后再对在高分辨率图像上进行预训练的网络进行精调会更有效。
在训练目标检测器时,可以对不同分辨率的目标使用不同的的网络结构进行分类,或者使用单独的结构对所有分辨率进行分类。由于在ImageNet或其他分类数据集中的预训练是有益的,同时在较大的目标实例中的filter对较小的目标实例的分类有帮助,因此对图像进行上采样及使用在高分辨率图像中预训练的网络优于特定的用于对小目标进行分类的网络。
2、图像的分辨率、目标实例的尺度以及数据多样性在检测中的影响:

检测器在1400×2000的分辨率上进行训练。
图像的分辨率影响:使用所有的800×1400与1400×2000图像进行训练,即800all与1400all。从表中数据可知,1400all的性能更好,因为检测器是在与之相同的分辨率进行训练,但是仍旧提升的有限,根据对中大目标实例分析可得,它们太大以至于不能正确分类。

因此,在高分辨率中训练能够更好地分类小目标,对于中大目标反而会降低性能。
特定尺度的检测器:使用1400×2000的分辨率来训练检测器,忽略所有的中大目标(80px),结果是上表中的1400<80px,用来消除大目标的有害影响,然而结果反而更差。

通过忽略中大目标(大约占所有实例的30%)损失了面部和姿势多样性的重要来源,以至于损害的性能高于通过消除大尺度目标提升的性能。
为什么一定认为消除大尺度目标能够提升检测器性能?
多尺度训练(MST):在训练过程中,使用在多分辨率中随机取样的图像来训练尺度不变的检测器。确保训练实例可以在不同的尺度中进行观测,但仍旧优于过小或过大的目标降低了性能。

因此,使用近似scaled的目标来训练检测器同时尽可能多地捕获目标中的多样性非常重要。
3、SNIP
SNIP是MST的改进版,只使用面部和姿势最多的多样性进行训练同时将尺度限制在合适的范围内。
在MST中每张图像在不同的分辨率下被检测,因此,在高分辨率中的大目标和在低分辨率中的小目标很难被分类。但是,每个目标实例都出现在多个尺度中,其中一些也出现在需要的尺度范围中。为了消除极限尺度(太大或太小)的目标,在训练时,只对处于给定范围内的尺度进行反向传播。

SNIP在训练过程中利用了所有的目标实例,有利于捕获面部以及姿势的所有的多样性,同时削弱了与训练网络的尺度空间上的域偏移。
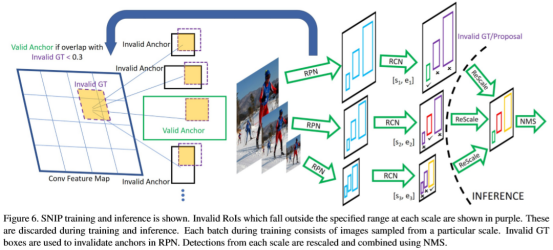
在训练过程中,仅当候选区域以及ground truth boxes在每种分辨率中的一个特定的size范围内才会标记为valid,否则为invalid。如,在分辨率i中,只有当RoI在[sic, eic]。同时RPN也使用所有的ground truth boxes来对anchor分配标签。最后,所有的与invalid的ground truth boxes间IoU>0.3的anchor被剔除(如,将其梯度设置为0)。在推断过程中,使用RPN为每个分辨率提取候选区域同时在各个分辨率下独立分类。在分类与bbox回归后,使用soft-NMS来对多分辨率的检测结果进行整合获得最终的bbox。
由于在池化后的RoIs的分辨率与预训练网络相匹配,因此在精调过程总网络更容易学习。

4、随机裁剪
主要为了迎合GPU的内存计算,对超过1000×1000分辨率的图像随机裁剪1000×1000的子图放进网络中进行计算,对结果的影响不大,或几乎毫无影响。
&思考与启发
1、既然在与训练的时候使用的分辨率相同的图像的结果最好,那么是否可以将CNN网络中的每一个层级提取出的特征图作为其采样得到的图像,因为通过更大的上下文信息比起仅通过下采样后的图像的信息特征更丰富。
2、图像金字塔中直接训练一个检测器,针对bbox,只有对应的bbox的尺度的anchor才放入检测器中。可以将图片进行上下采样,每个图像中使用同样范围的anchor;或者直接使用RPN找到原图中的anchor,然后进行金字塔中的缩放,然后将对应部分输入到检测器中。





