我用Awesome-Graphs看论文：解读Pregel

Pregel论文：《Pregel: A System for Large-Scale Graph Processing》

上次向大家分享了论文图谱项目Awesome-Graphs的介绍文章《论文图谱当如是：Awesome-Graphs用200篇图系统论文打个样》，这次我们就拿图计算系统的奠基文章Pregel开篇，沿着论文图谱的主线，对图计算系统的论文内容进行解读，下篇预报Differential dataflow。

对图计算技术感兴趣的同学可以多做了解，也非常欢迎大家关注和参与论文图谱的开源项目：

Awesome-Graphs：https://github.com/TuGraph-family/Awesome-Graphs
OSGraph：https://github.com/TuGraph-family/OSGraph

提前感谢给项目点Star的小伙伴，接下来我们直接进入正文！

摘要

使用Pregel计算模型编写的程序，包含一系列的迭代。在每个迭代中，图的点可以接收上一个迭代发送的消息，也可以给其他的点发送消息，同时可以更新自身和出边的状态，甚至可以修改图的拓扑结构。这种以点为中心的计算方式可以灵活的表示大量的图算法。

1. 介绍

大规模图处理面临的挑战：

图算法的内存访问局部性较差。
单个点上的计算量较少。
执行过程中并行度改变带来的问题。
分布式计算过程的机器故障问题。

大规模图算法的常见实现方式：

为特定的图定制的分布式实现【通用型差】
基于现有的分布式计算平台【如MR，性能、易用性不足】
使用单机图算法库【如BGL、LEDA、NetworkX、JDSL、GraphBase、FGL，限制了图的规模】
使用已有的图计算系统【如Parallel BGL、CGMgraph，缺少容错机制】

Pregel计算系统的设计灵感来源于Valiant的BSP模型：

计算是由一系列的迭代组成，这些迭代被称为超步（Superstep）。
每次超步框架都会并行地在点上执行用户的UDF，描述了点V在超步S的行为。
UDF内可以读取S-1超步发送给点V的消息，并将新的消息发送给S+1超步的点。
UDF内可以修改点V以及其出边的状态。
通常消息是沿着点的出边方向进行发送的，但也可以发送给指定ID对应的点。

2. 模型

输入

Pregel计算模型的输入是一个有向图：

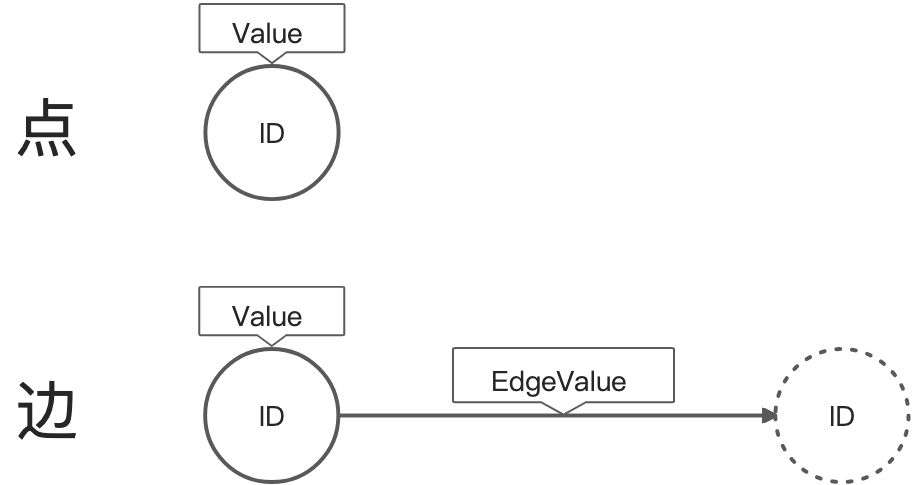
点使用string类型的ID进行区分，并有一个可修改的用户自定义类型value。
有向边与源点关联，包含可修改的用户自定义类型value和目标点ID。

计算

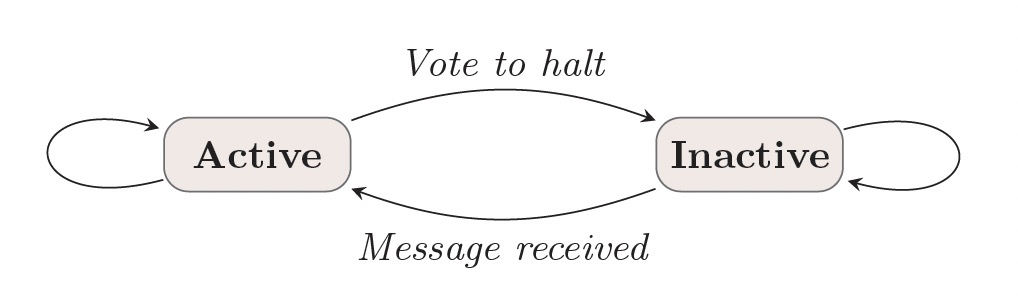
Pregel计算模型运行一系列超步直到计算结束，超步之间通过全部同步点（Barrier）进行分割。每个超步中点上的计算都是并行的，当所有的点都是inactive状态且没有消息传递时，计算终止。

输出

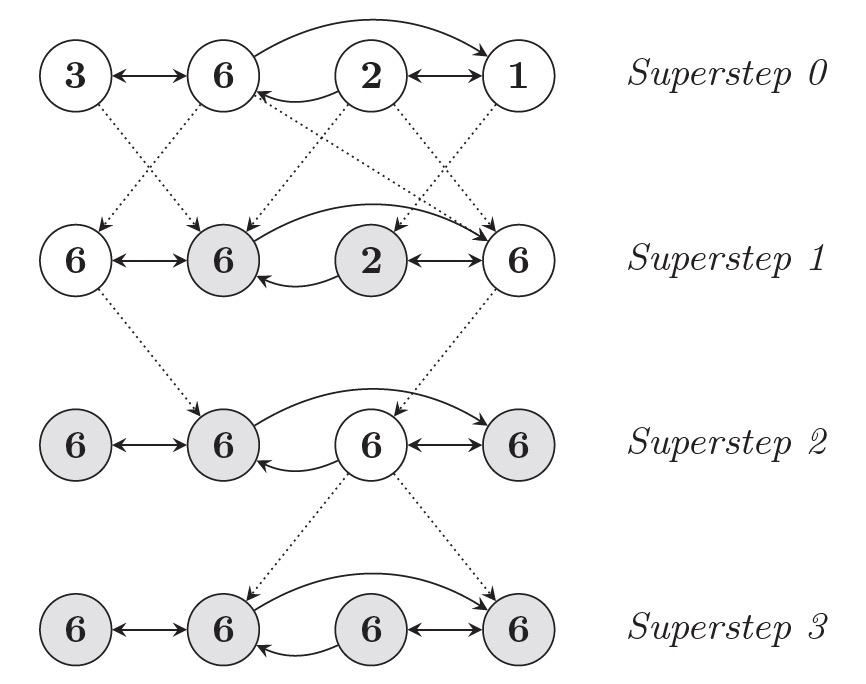
Pregel计算模型的输出是所有点输出值的集合，通常是和输入图同构的有向图。但这不是绝对的，因为计算过程中可以对点/边进行新增和删除操作。

讨论

Pregel使用消息传递模型，而非远程读取或者其他类似共享内存的方案：

消息传递具备足够的表达能力，而不必非要使用远程读取的方式。
远程读取的延迟很高，使用异步+批量的消息传递方式，可以降低这个延迟。（蕴含push语义）

使用链式MR实现图算法的性能问题：

Pregel将点/边保存在执行计算的机器上，仅使用网络传递信息。MR的实现方式需要将图状态从一个stage转换到另一个stage，提高了通信和序列化的开销。
一连串的MR作业的协调增加了图计算任务的复杂度，而使用Pregel的超步可以避免该问题。

3. API

template <typename VertexValue, typename EdgeValue, typename MessageValue>
class Vertex {
  public:
    virtual void Compute(MessageIterator* msgs) = 0;
    
    const string& vertex_id() const;
    int64 superstep() const;
    
    const VertexValue& GetValue();
    VertexValue* MutableValue();
    OutEdgeIterator GetOutEdgeIterator();
    
    void SendMessageTo(const string& dest_vertex, const MessageValue& message);
    void VoteToHalt();
};

Vertex：Pregel程序继承于Vertex类，模版参数对应点值、边值和消息的类型。
Compute：每次超步在每个点上执行的UDF。
GetValue：获取点的值。
MutableValue：修改点的值。
GetOutEdgeIterator：获取出边的迭代器，可以对出边的值进行读取和修改。
点的值和出边是跨超步持久化的。

3.1 消息传递

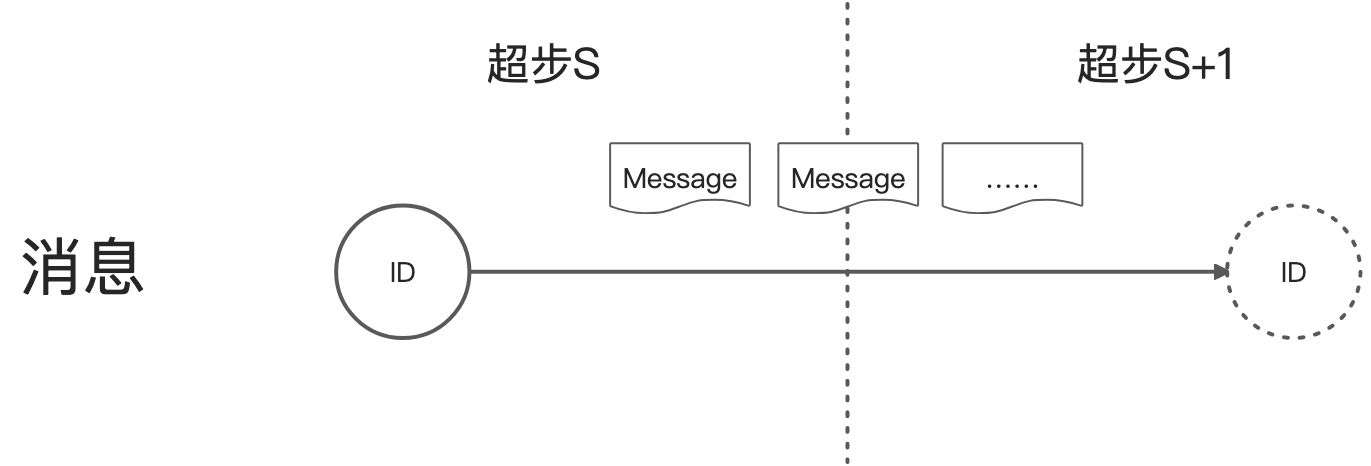
点可以发送任意多的消息。
所有在超步S发送给点V的消息，可以在超步S+1时使用迭代器获取。
消息顺序不做保证，但能保证一点会被传输且不会去重。
接收消息的点不一定是邻居点，即消息不一定沿着出边发送。

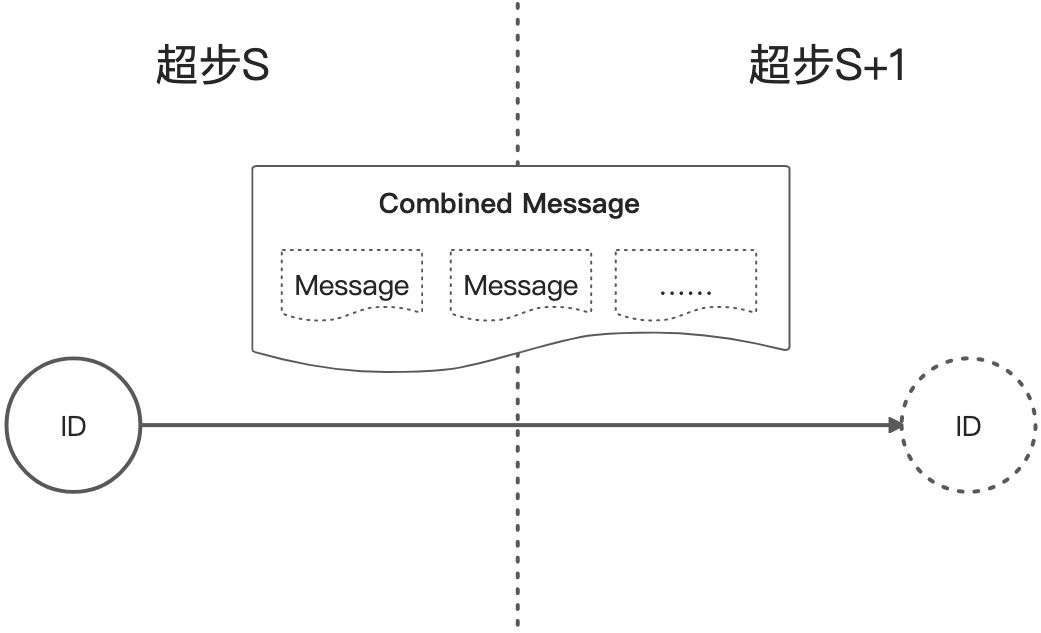
3.2 连接器（Combiner）

当给点发送消息，尤其是目标点在其他的机器上时，会产生一定的开销，通过用户层面自定义Combiner可以降低这样的开销。比如发送给同一个点的消息的合并逻辑是求和，那么系统在发送消息给目标点之前就预先求和，将多个消息合并为一个消息，降低网络的和内存的开销。

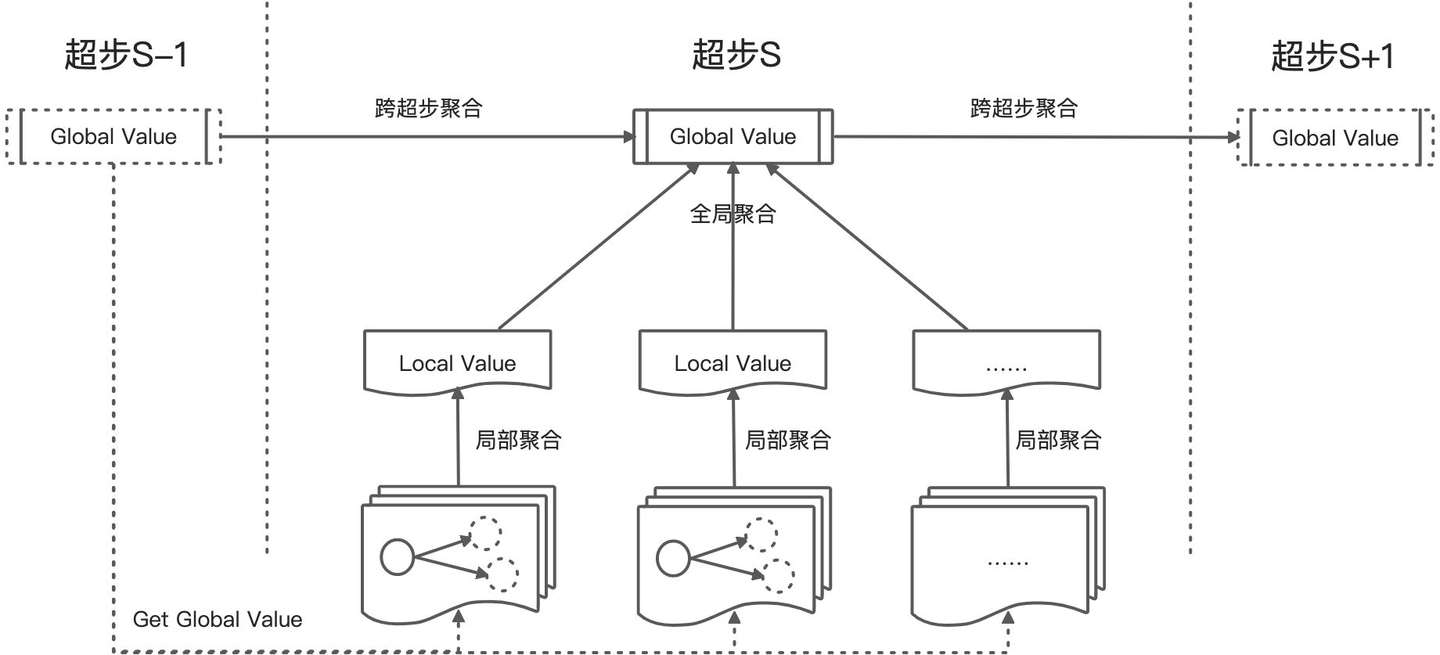
3.3 聚合器（Aggregator）

Pregel的聚合器提供了一种全局通信的机制：

每个超步S中的点都可以提供一个值。
系统使用reduce算子将所有的值规约为一个全局值，如max、min、sum。
这个全局值对超步S+1中的所有点可见。
聚合器可以提供跨超步的聚合能力。

使用场景：

统计特征：对点的出度求和可以计算图的边数。
全局协调：超步中等待所有的点满足一定条件再继续计算；算法中选举一个点作为特殊角色。
跨超步聚合：根据超步中对边的新增/删除自动维护全局边数量；Δ-stepping最短路径算法。

3.4 修改拓扑

修改冲突解决策略：

删除边优先于删除点。
删除操作优先于新增操作。
新增点优先于新增边。
用户自定义冲突策略。
最后执行compute函数。

3.5 输入输出

构图与图计算分离。
自定义Reader/Writer。

4. 实现

4.1 基本架构

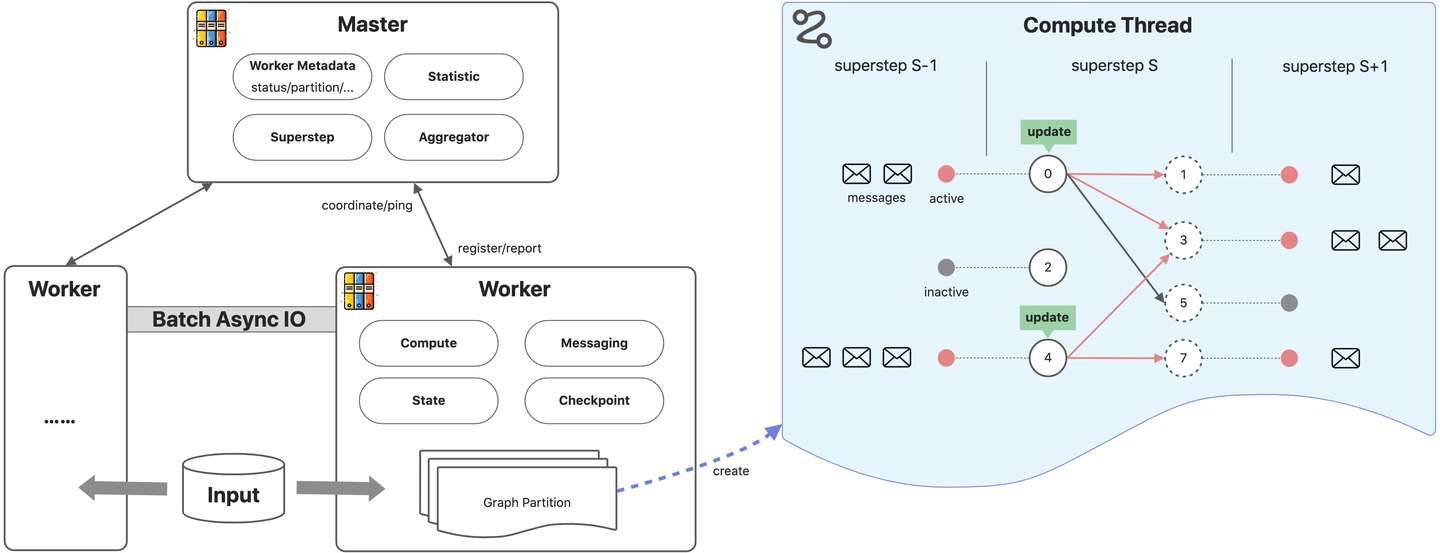
Pregel程序执行流程：

用户程序被拷贝到master和worker节点上。master用于协调worker节点，worker节点通过名字服务向master注册信息。
master决定图的分区，默认hash(点ID)%分区数。worker负责维护图分区的状态、执行compute函数、收发其他worker的消息。
master为worker分配用户输入，输入的划分和图切分是独立的。如果输入和图分片刚好在一个worker上则立即更新对应数据结构，否则shuffle到其他worker。输入加载完成后，点被初始化为active状态。
master指导worker执行超步，worker为每个分区启动一个线程，在active状态的点上执行compute函数，接收上个超步传递的消息。worker执行结束后，会向master汇报下次超步active的点数。
超步会不断的执行，直到没有active的点以及消息为止。计算结束后，master通知worker保存图分片上的计算结果。

4.2 错误容忍

容错机制通过checkpoint方式实现：

超步开始之前，master通知woker将图状态保存到持久化存储。
图状态包含：点值、边值、输入消息，以及master上的aggregator的值。
master通过ping消息检测worker的状态，一旦失联worker计算终止，master将worker标记为failed状态。
master将失败的worker上对应的分区分配到其他存活的worker，其他worker从checkpoint加载图状态。
checkpoint可能比出错时的上次超步领先多个超步（不一定每次超步都会checkpoint）。
Confined Recovery会将发出的消息持久化，以节省恢复时的计算资源，但要求计算是确定的。

4.3 Worker实现

worker维护了图分片上每个点的状态，状态包含：当前点值、出边列表（边值+目标点）、输入消息队列、active标记。
考虑性能，点active标记和输入消息队列独立存储。
点/边的值只有一份，点active标记和输入消息队列有两份（当前超步和下一超步）。
发送给其他worker点上的消息先buffer再异步发送，发给本地的点的消息直接存放到目标点的输入消息队列。
消息被加入到输出队列或者到达输入队列时，会执行combiner函数。后一种情况并不会节省网络开销，但是会节省用于消息存储的空间（compute内蕴含combine语义）。

4.4 Master实现

协调worker，在worker注册到master分配id。保存worker的id、存活状态、地址信息、分区信息等。
master的操作包括输入、输出、计算、保存/恢复checkpoint。
维护计算过程中的统计数据和图的状态数据，如图大小、出度分布、active点数、超步的耗时和消息传输量、aggregator值等。

4.5 聚合器

worker先进行分片的部分聚合。
全局聚合使用tree方式规约，而不是pipeline方式，提高CPU并行效率。
全局聚合值在下个超步被发送给所有worker。

5. 应用

5.1 PageRank

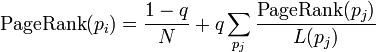
class PageRankVertex : public Vertex<double, void, double> {
  public:
    virtual void Compute(MessageIterator* msgs) {
      if (superstep() >= 1) {
        double sum = 0;
        for (; !msgs->Done(); msgs->Next())
        sum += msgs->Value();
        *MutableValue() = 0.15 / NumVertices() + 0.85 * sum;
    }
    if (superstep() < 30) {
      const int64 n = GetOutEdgeIterator().size();
      SendMessageToAllNeighbors(GetValue() / n);
    } else {
      VoteToHalt();
    }
  }
};

5.2 最短路径

class ShortestPathVertex: public Vertex<int, int, int> {
  void Compute(MessageIterator* msgs) {
    int mindist = IsSource(vertex_id()) ? 0 : INF;
    for (; !msgs->Done(); msgs->Next())
      mindist = min(mindist, msgs->Value());
      if (mindist < GetValue()) {
        *MutableValue() = mindist;
        OutEdgeIterator iter = GetOutEdgeIterator();
        for (; !iter.Done(); iter.Next())
          SendMessageTo(iter.Target(), mindist + iter.GetValue());
    }
    VoteToHalt();
  }
};

class MinIntCombiner : public Combiner<int> {
  virtual void Combine(MessageIterator* msgs) {
    int mindist = INF;
    for (; !msgs->Done(); msgs->Next())
      mindist = min(mindist, msgs->Value());
    Output("combined_source", mindist);
  }
};

5.3 二分图匹配

计算流程：

阶段0：左边集合中那些还未被匹配的顶点会发送消息给它的每个邻居请求匹配，然后会无条件的VoteToHalt。如果它没有发送消息(可能是因为它已经找到了匹配，或者没有出边)，或者是所有的消息接收者都已经被匹配，该顶点就不会再变为active状态。
阶段1：右边集合中那些还未被匹配的顶点随机选择它接收到的消息中的其中一个，并发送消息表示接受该请求，然后给其他请求者发送拒绝消息。然后，它也无条件的VoteToHalt。
阶段2：左边集合中那些还未被匹配的顶点选择它所收到右边集合发送过来的接受请求中的其中一个，并发送一个确认消息。左边集合中那些已经匹配好的顶点永远都不会执行这个阶段，因为它们不会在阶段0发送消息。
阶段3：右边集合中还未被匹配的顶点最多会收到一个确认消息。它会通知匹配顶点，然后无条件的VoteToHalt，它的工作已经完成。
重复以上过程，直到所有的节点匹配完成。

5.4 半聚类

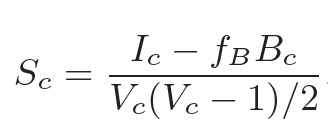
【算法实现要补充一下资料】

6. 实验

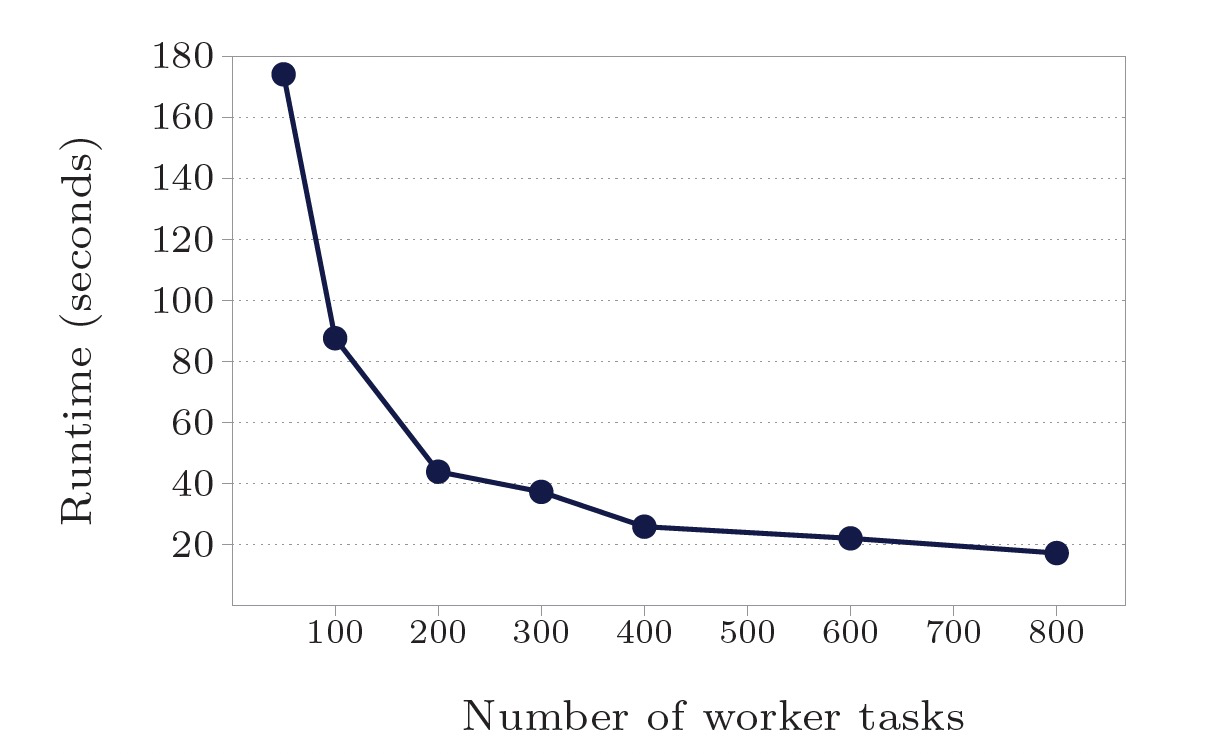
使用最短路径算法测试：

点/边规模10亿：worker数50-800，计算时间174s-17.3s，16x worker加速10x。
worker数800：点/边规模10亿-500亿，计算时间17.3s-702s，计算时间线性增长。

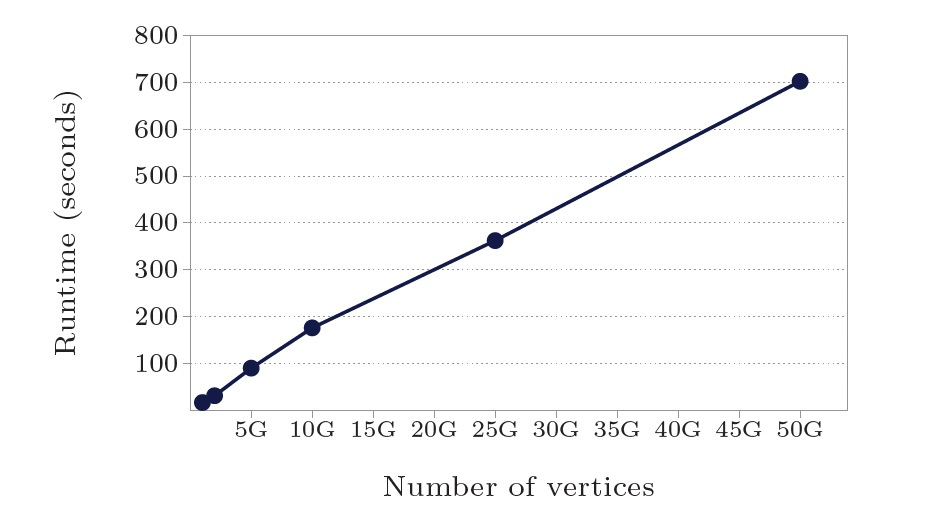
总结

Pregel受BSP计算模型启发，采用了“think like a vertex”方式的编程API。
Pregel可以满足10亿规模的图计算的性能、扩展性和容错能力。
Pregel被设计于稀疏图上的计算，通信主要发生在边上，稠密图中的热点会导致性能问题。

posted @ 2024-07-29 16:32 Florian 阅读(147) 评论(0) 编辑收藏举报

刷新页面返回顶部