poj 2559Largest Rectangle in a Histogram（单调栈简单模板题）

Largest Rectangle in a Histogram

Time Limit: 1000MS		Memory Limit: 65536K
Total Submissions: 34844		Accepted: 11339

Description

A histogram is a polygon composed of a sequence of rectangles aligned at a common base line. The rectangles have equal widths but may have different heights. For example, the figure on the left shows the histogram that consists of rectangles with the heights 2, 1, 4, 5, 1, 3, 3, measured in units where 1 is the width of the rectangles:

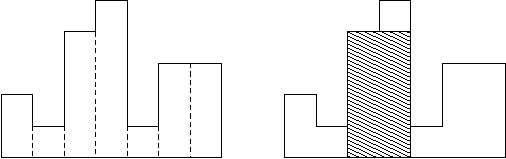
Usually, histograms are used to represent discrete distributions, e.g., the frequencies of characters in texts. Note that the order of the rectangles, i.e., their heights, is important. Calculate the area of the largest rectangle in a histogram that is aligned at the common base line, too. The figure on the right shows the largest aligned rectangle for the depicted histogram.

Input

The input contains several test cases. Each test case describes a histogram and starts with an integer n, denoting the number of rectangles it is composed of. You may assume that 1<=n<=100000. Then follow n integers h₁,...,h_n, where 0<=h_i<=1000000000. These numbers denote the heights of the rectangles of the histogram in left-to-right order. The width of each rectangle is 1. A zero follows the input for the last test case.

Output

For each test case output on a single line the area of the largest rectangle in the specified histogram. Remember that this rectangle must be aligned at the common base line.

Sample Input

7 2 1 4 5 1 3 3
4 1000 1000 1000 1000
0

Sample Output

8
4000

Hint

Huge input, scanf is recommended.

Source

Ulm Local 2003

 

给出一串柱的高度，求最大矩形面积；

以2，1，4，5，1，3，3为例

设栈内的元素为一个二元组(x,y),x表示矩形的高，y表示宽；

建立一个单调递增栈，所有元素各进栈和出栈一次即可。每个元素出栈的时候更新最大的矩形面积。

（2，1）：进栈，

（1，1）：因为x1<2    (2,1)出栈，y++；此时矩形（1，2）；

（4，1）：进栈；

（5，1）：进栈；

（1，1）：准备进栈，（5，1）出栈；y++；此时矩形（4，2）；

                  （4，2）出栈y++；此时矩形（1，3）；（1，3）出栈；y+=2（之前矩形（1，2）的高），此时矩形（1，5）

（3，1）：进栈，

（3，1）：准备进栈（3，1）出栈；y++；此时矩阵（3，2）；

  输入结束

 （3，2）出栈；y+=5；此时矩阵（1，5）；

 

 

代码：

#include <iostream>
#include <cstdio>
using namespace std;

const int N = 100005;

struct Elem
{
int height;
int count;
};

Elem stack[N];
int top;

int main()
{
int height, n;
long long ans, tot, tmp;
while (~scanf("%d", &n) && n)
{
top = 0;
ans = 0;
for (int i = 0; i < n; ++i)
{
scanf("%d", &height);
tmp = 0;
while (top > 0 && stack[top - 1].height >= height)
{
tot = stack[top - 1].height * (stack[top - 1].count + tmp);
if (tot > ans) ans = tot;
tmp += stack[top - 1].count;
--top;
}
stack[top].height = height;
stack[top].count = 1 + tmp;
++top;
}
tmp = 0;
while (top > 0)
{
tot = stack[top - 1].height * (stack[top - 1].count + tmp);
if (tot > ans) ans = tot;
tmp += stack[top - 1].count;
--top;
}
printf("%lld\n", ans);
}
}