图说线性表-搞懂链表从这篇文章开始
上篇文章是数据结构的基础部分,主要介绍了一些注意事项。
今天开始线性表部分的梳理,线性表主要分为了基础概念和基本操作两大部分,由于某些过程或概念比较抽象,我添加了部分图示,希望能够把这些抽象的东西直观的表达出来。
基本操作模块重点主要在单链表和顺序表两部分,本文着重梳理了线性表插入、删除、查询等基础方法并搭配了部分实例供参考。
1 基本概念
对于线性表来说,它是一组相同元素的有限序列,元素的个数就是线性表的长度,当元素个数为 0 时,线性表就是空表。
数据结构包括逻辑结构、存储结构和算法。线性表的基本概念这里主要看线性表的逻辑结构和存储结构就可以了。
1.1 线性表的逻辑结构
线性表的逻辑特性很好理解,由于是相同元素的有限序列,可以类比生活中的排队场景:
-
只有一个表头元素,表头元素没有前驱
-
只有一个表尾元素,表尾元素没有后继
-
除表头表尾元素外,其他元素都只有一个前驱和一个后继
1.2 线性表的存储结构
线性表的存储结构有两类:顺序表和链表。
特性:占用一块连续的存储空间,随机读取,插入(删除)时需要移动多个元素
-
链表
链表包含指针域与数值域两部分,因此存储不需要占用连续空间,由指针来连接记录结点位置信息,通过前驱节点的指针找到后继结点。
特性:动态分配空间,顺序读取,插入(删除)时不需要移动元素。
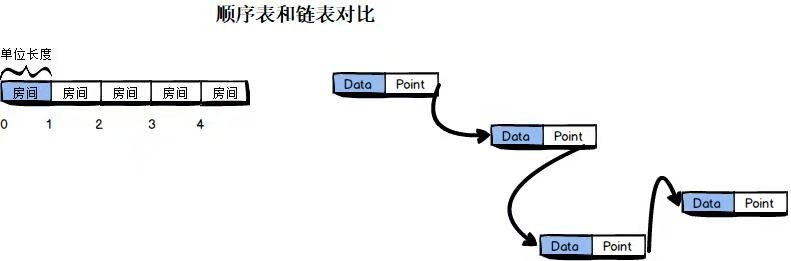
链表的分类如下:
-
单链表
每个节点包含数据域与指针域,单链表分为带头节点的和不带头结点的。
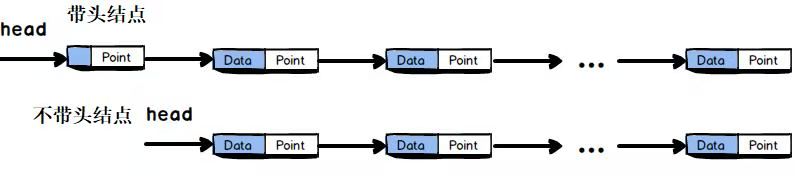
-
带头结点的链表中,头结点的值域不含任何储存数据的信息,从头结点的下一个结点开始存储数据信息,头结点的指针 head 始终不等于 NULL,当 head -> next 等于 NULL 时,此时链表为空
-
不带头结点的链表中,头指针直接指向第一个结点,第一个结点就开始存储数据信息,当 head 等于 NULL 时链表为空。
注意区分头结点和头指针:
-
头指针: 指向链表的第一个结点,无论带不带头结点都有头指针
-
头结点:只有带头结点的链表才有,值域只存描述链表属性的信息,此时头指针指向头结点始终不为 NULL 。
-
双链表
双链表在单链表的基础上添加一个指针域指向前驱结点,可以通过不同的指针域找到其前驱结点或后继节点。
-
带头结点的双链表,类似单链表,当 head -> next 为空链表为空
-
不带头结点的双链表 当 head 为空时链表为空
-
循环单链表
在单链表的基础上,将最后一个结点的指针域指向表头结点即可。
-
带头结点的循环单链表,当 head 等于 head -> next 时 链表为空
-
不带头结点的循环单链表,当 head 为 空时链表为空
-
循环双链表
在双链表的基础上,将最后一个结点的尾指针指向第一个结点,将第一个结点的头指针指向最后一个结点。
-
不带头结点的循环双链表 当 head 为空时 链表为空
-
带头结点循环双链表 当 head -> next (尾指针) 和 head -> prior (头指针) 任一一个等于 head 时 ,链表为空,事实上满足以下任一条件,链表都为空:
head -> next = head head ->prior = head head -> next = head && head ->prior = head head -> next = head || head ->prior = head
-
静态链表
静态链表与一般链表不同,它一般来自于数组,数组中每个节点包含两个分量,一个是数据元素,一个是指针分量。
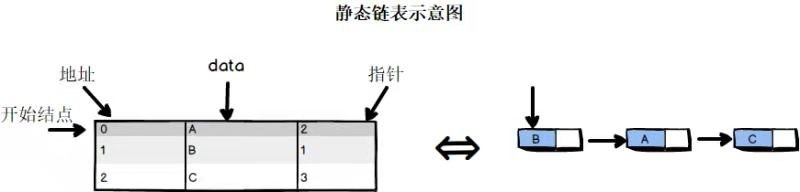
链表分类可以理解成公路的分类,单链表像单行道,只能由表头走向表尾;双链表像双行道可以从表头走向表尾,也可以反过来;循环单链表像环形道,表头表尾链接在一起;循环双链表像环形立交桥,表头表尾连接在一起,而且正向反向都可以。
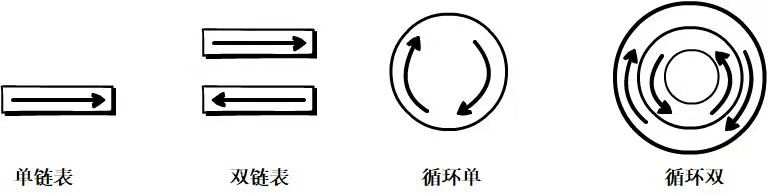
1.3 顺序表和链表的比较
顺序表和链表的比较也算是面试中的经典题目了,这里主要分为时间角度和空间角度进行对比:
-
时间角度-存取方式的区别
-
顺序表支持随机读取(查询快),时间复杂度为 O(1);
-
链表只能顺序读取(查询慢),时间复杂度为 O(n)
-
时间角度-插入(删除)时需要移动元素的个数区别
-
顺序表需要平均需要移动近一般的元素,时间复杂度为 O(n),增删慢
-
链表不需要移动元素,时间复杂度为 O(1),增删快
-
空间角度-存储分配方式的区别
-
顺序表内存一次性分配完,占用连续存储空间
-
链表存储空间需要多次分配,动态分配,来一个分配一个
-
空间角度-存储密度区别 (存储密度=结点值域所占存储量/结点结构所占存储量)
2 线性表的基本操作
操作模块主要为单链表和顺序表两部分,着重梳理它们插入、删除、查询等基础方法。
2.1 结构体定义
-
顺序表定义
#define maxSize 100; struct typedef { int data [maxSize];//定义顺序表存放元素的数据 int length; //定义顺序表的长度 }Sqlist; // 顺序表类型定义
-
单链表定义
struct typedef ListNode { int data, // 值域 struct ListNode *next;//指针域 }ListNode; //定义链表的结点类型
-
双链表定义
struct typedef DLNode { int data; //值域 struct DLNode *prior;//前驱结点指针 struct DLNode *next;//后继结点指针 }DLNode;//定义双链表结点类型
2.2 顺序表的操作
操作部分就要结合例题来看了,顺序表部分的操作类似 Java 中 数组的操作十分类似。
-
顺序表的插入操作
例1:已知一个顺序表 L,其中元素递增有序,设计一个算法,插入一个元素 m (int 型),后保持该顺序表仍然递增有序排列。(假设每次插入都是成功的)
分析题目可以看出两点:
1 原顺序表 L 已经排序,递增有序
2 插入 m 元素后仍然递增有序,递增排序不变
需要进行的步骤如下:
1 找出插入元素的位置
2 移动位置后面的元素 (从大下标的开始移动)
3 插入元素
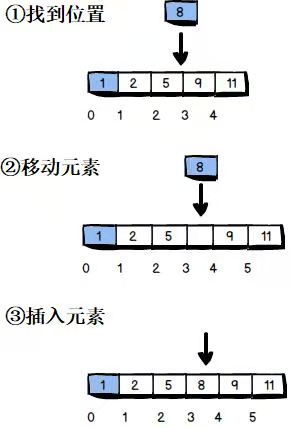
代码:
/** * 查找元素的方法 * l 顺序表 * m 需要查找的元素 */ int findElement(SqList l,int m) { int i; for(i=0;i<l.length;++i) { if(m < l.data[i]) { return i; // 找到第一个比 m 大的元素的位置返回 } } return i;//如果整个顺序表都不大于m,则返回最后的位置 } /** * 新增元素的方法 * l 顺序表 * m 需要新增的元素 */ void insertElement(SqList &l,int m) // 顺序表本身需要发生变化所以传入的是引用型 { int p,i; p = findElement(l,m); for(i=l.length-1;i>=p;--i) // 条件为 i>=p ,p位置的元素也需要移动 { l.data[i+1] = l.data[i];//从顺序表的最后开始向右移动 } l.data[p] = m; ++(l.length); }
-
顺序表的删除操作
删除操作与插入操作相反,删除掉元素后,将后续元素都前移即可。
例2:删除顺序表L中下标为 p (0<=p<=l.length-1)的元素,成功返回 1,否则返回0,并将删除的数值赋值给 e。
分析题目可知:
1 需要删除的元素位置为 p
2 删除元素前需要将值赋值给 e
需要进行的步骤如下:
1 找到需要删除的元素的位置,题目已提供 p (如果没有提供位置,需要循环查找)
2 将删除元素 p 赋值给元素 e
3 将P后的元素左移 (与插入不同,删除要从小下标的开始移动)
代码:
/** * 删除元素的方法 * l 顺序表 * p 需要删除元素的位置 * e 删除元素赋值的变量 */ int deleteElement(SqList &l,int p,int &e)//需要改变的元素用引用变量 { int i; if( p < 0 || p > l.length -1) return 0; e = l.data[p]; for(i=p;i < l.length-1;++i){//判断条件应为 i < l.length-1 ,如果为 i < l.length i+1 会下标越界 l.data[i] = l.data[i+1]; } --(l.length) return 1; }
2.3 单链表的操作
链表的相关操作是数据结构中比较常用的,这部分需要划重点。
-
单链表的插入操作
单链表的插入主要有尾插法、头插法两种。
尾插法比较常规就是将新加的结点依次链接到链表最后一个结点。
尾插法: /** * C 准备要插入的链表 * a 数组,要插入到链表中的元素 * n 将要插入的节点数 * * *&C 指针型变量在函数体中需要改变的写法 * 顺序表 &L ( 普通变量 &m )引用型变量需要改变的写法 * */ void createListR(ListNode *&C,int a[],int n) // 要改变的变量传引用型 { ListNode *s,*r; // 指针r 准备指向 C,s准备指向要插入的节点 int i; // 循环使用的变量 C = (ListNode*) malloc (sizeof(ListNode)); //申请 C 的头结点空间 C -> next = NULL; // 申请头结点空间时一定不要忘记将头结点指针指向NULL r = C; //r 指向头节点 for(i=0;i<n,++i) { s = (ListNode*)malloc(sizeof(ListNode));//s 指向新申请的节点 s -> data = a[i]; // 值域赋值 r->next = s; // 插入新的结点 r = r->next;// 指针移动到终端结点,准备在终端插入新结点 } r ->next = NULL;//插入完成后将 ,终端结点的指针域设置为NULL,C 建立完成 }
头插法则是将新加的结点始终插入在头结点的后面,因此越早插入的结点在链表中的位置实际上越靠后。
图示:
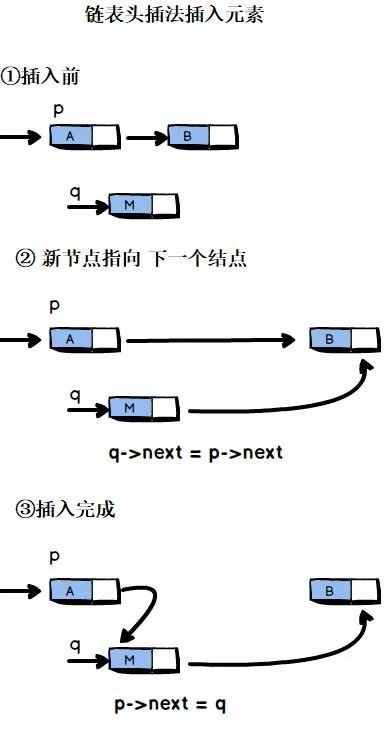
头插法: /** * C 准备要插入的链表 * a 数组,要插入到链表中的元素 * n 将要插入的节点数 * * *&C 指针型变量在函数体中需要改变的写法 * 顺序表 &L ( 普通变量 &m )引用型变量需要改变的写法 * */ void createlistF(ListNode *&C,int a[],int n) { ListNode *s; int i ; C = (ListNode *)malloc( sizeof(ListNode)); C -> next = NULL; for(i=0;i<n;++i) { s = (ListNode*)malloc(sizeof(ListNode)); s->data = a[i]; //头插法 s->next = C->next;//图中第二步 C->next = s;//图中第三步 } }
-
单链表的删除操作
链表的删除操作就比较简单了,要删除第m个结点,需要找到第 m-1 个结点,将第 m-1个结点的指针指向 m+1 个结点就可以了。
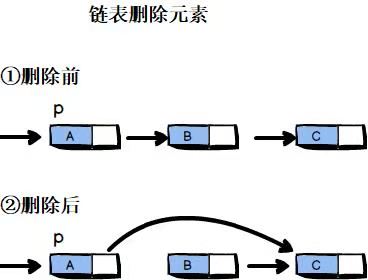
相关操作:
q = p->next;//先将要删除的结点赋值给q
p->next = p->next->next; //第二步操作
free(q);
-
单链表的查找操作
例 3: 查找链表 L(带头结点) 中是否有一个值为 m 的节点,如果有则删除该节点,返回1,否则返回0.
/** * L 查找的链表 * m 链表值域查找的值 */ int deleteElement(ListNode *L,int m ) { ListNode *p,*q; // 定义一个指针 p,在链表中一直往下找 , q作为删除节点的 p = L; while(p->next != NULL) { if(p->next->data == x){ // 注意此处是 p->next->data ==x,而不是 p->next == x break; } p = p -> next; } if(p -> next == NULL) { return 0; } else { q = p->next; // 要删除的节点是 p->next ,q p->next = p->next->next; free(q); return 1; } }
-
单链表的合并操作
链表的基本的查询 、插入、 删除操作的重点部分已经回顾完了,下面来看看 leetCode 的例题---合并链表:
题目如下:
将两个升序链表合并为一个新的 升序 链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。
示例:
输入:1->2->4, 1->3->4 输出:1->1->2->3->4->4
思路:
1 升序的两个链表,合并成一个升序新链表
2 创建头指针,使用尾插法循环比较 两个链表的值,把值小的插入到头结点后,移动指针
3 如果循环结束后某一个链表指针没有移动到末尾,将新链表末尾指向这个指针的结点
图解:
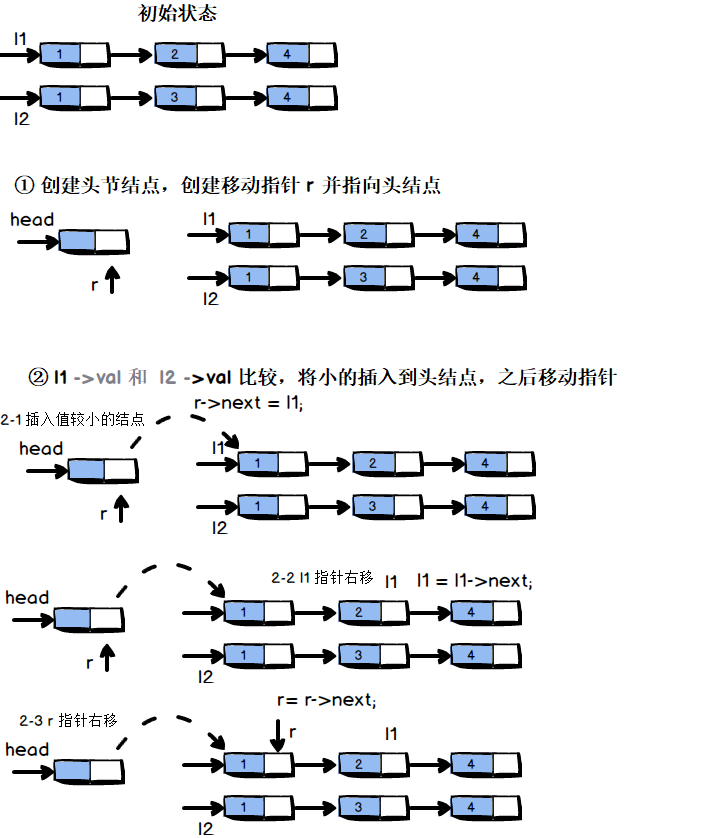
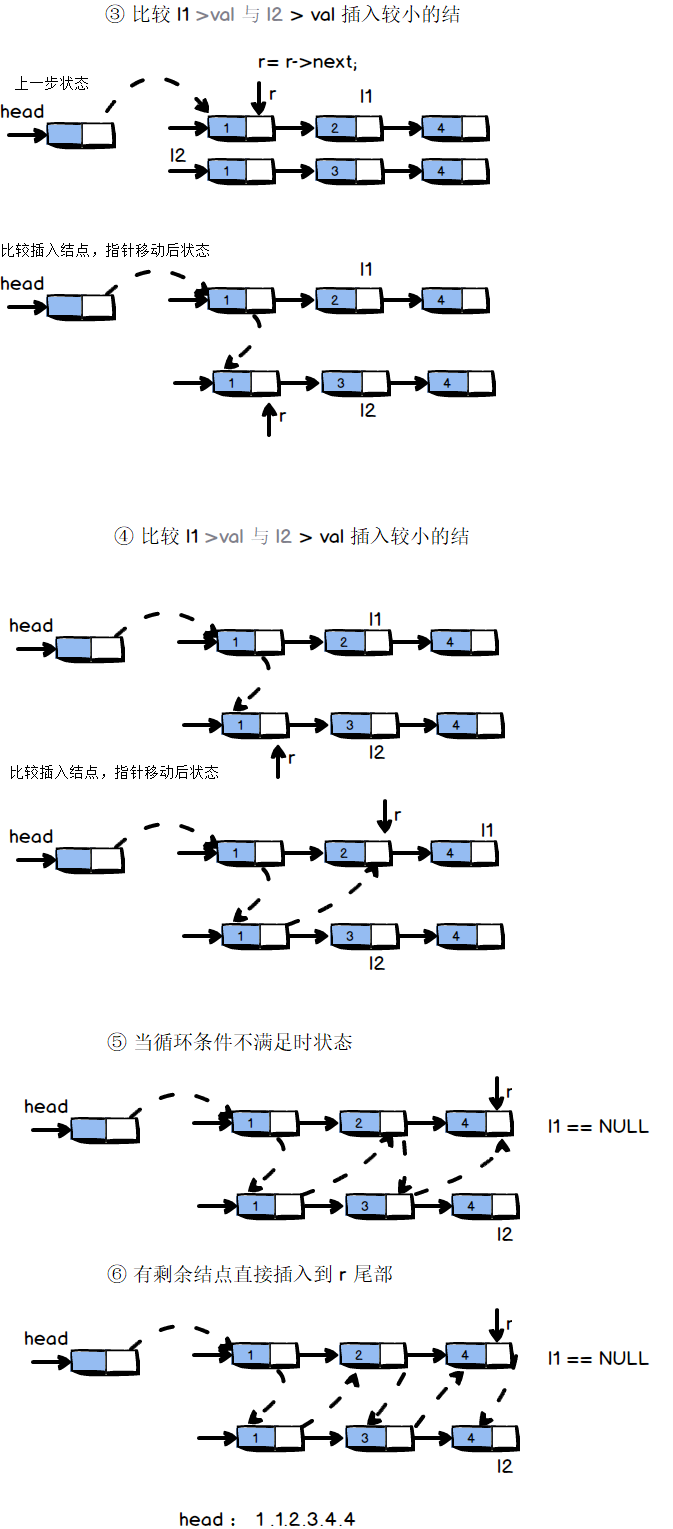
题解:
常规解法: /** * Definition for singly-linked list. * struct ListNode { * int val; * struct ListNode *next; * }; */ struct ListNode* mergeTwoLists(struct ListNode* l1, struct ListNode* l2){ struct ListNode *head = (struct ListNode*)malloc(sizeof(struct ListNode));//申请头结点空间 struct ListNode *r = head;//定义移动指针 r ,r始终指向终端结点 while( l1 !=NULL && l2 != NULL){ if(l1 -> val <= l2 -> val){ r -> next = l1;//将 r->next指向 l1 l1 = l1->next; //l1 指针前移 r = r->next; //r 指针前移 }else{ r -> next = l2; l2=l2 -> next; r = r-> next; } } r->next = NULL; if(l1 != NULL){ // 如果循环插入结束后仍有剩余结点,直接插入到末尾 r -> next = l1; } if(l2 != NULL){// 如果循环插入结束后仍有剩余结点,直接插入到末尾 r -> next = l2; } return head ->next;//不用返回头结点 }
上面的解法结果没什么问题,就是我们新创建了一个头结点,如果置之不理的话,可能会导致内存泄漏。
下面是不创建头结点的解法,只是再开始的时候巧妙的使用两个链表中最小表头为新链表的头结点,后面操作类似
不申请头结点解法: /** * Definition for singly-linked list. * struct ListNode { * int val; * struct ListNode *next; * }; */ struct ListNode* mergeTwoLists(struct ListNode* l1, struct ListNode* l2){ if(l1 == NULL) return l2; if(l2 == NULL) return l1; struct ListNode *head;//定义头指针 if (l1->val < l2->val){ head = l1; //如果 l1 表头元素值较小 ,将头指针指向l1 l1 = l1->next;// l1 指针右移 }else{ head = l2; //如果 l2 表头元素值较小 ,将头指针指向l1 l2 = l2->next;//l2 指针右移 } struct ListNode *r = head; // l1,l2一直向后遍历元素,向head中按序插入,直至l1或l2为NULL while(l1 && l2){ if(l1->val < l2->val){ r->next = l1; l1 = l1->next; r = r->next; }else{ r->next = l2; l2 = l2->next; r = r->next; } } // l1或l2为NULL,此时将不会空的链表接到最后即可 r->next = l1 ? l1 : l2; return head; }
以上不同的解法都是使用了链表的尾插法,因为尾插法正好符合题目的要求,新插入的结点也是依次递增的。
如果题目要求变成要求 将两个升序链表合并为一个新的 降序 链表并返回,这时使用头插法就比较合适了。
合并为一个新的 降序 链表,头插法: /** * Definition for singly-linked list. * struct ListNode { * int val; * struct ListNode *next; * }; */ struct ListNode* mergeTwoLists(struct ListNode* l1, struct ListNode* l2){ struct ListNode *head = (struct ListNode*)malloc(sizeof(struct ListNode));//申请头结点空间 head ->next =NULL; struct ListNode *r;//定义移动指针 r ,r始终指向终端结点 while( l1 !=NULL && l2 != NULL){ if(l1 -> val <= l2 -> val){ r = l1; // r 指针指向 l1 结点 l1 = l1->next;//l1 结点右移 r->next = head -> next ;//r->next 指向头结点的下一个结点,见头插法图 head ->next = r; // 将 r 赋值给头结点的下一个结点 }else{ r = l2; l2 = l2->next; r->next = head->next; head->next = r; } } while(l1){ // 如果循环插入结束后仍有剩余结点,循环插入到头结点后 r = l1; l1 = l1->next; r->next = head -> next ; head ->next = r; } while(l2){// 如果循环插入结束后仍有剩余结点,循环插入到头结点后 r = l2; l2 = l2->next; r->next = head->next; head->next = r; } return head ->next;//不用返回头结点 }
以上就是本文的所有内容了,最后的例题只是抛砖引玉,单链表的好多复杂的操作,有兴趣的可以去找题刷刷~
最后,顺序表和单链表的操作还是比较重要的,后续双链表、循环链表的操作基本都是在单链表的基础上演变而来的,搞懂以上基础部分,其他的演变自然也就迎刃而解了。
PS: 关注“大数据江湖”公众号, 后台回复 "链表合并",查看更多精彩内容。
— THE END —



