入门学算法_堆排序、树遍历、生产消费模型
程序员的基本功包括数据结构与算法、操作系统、数据库原理、网络等等,这些提升内功的东西是需要花费长时间去练习的,也只有这些东西才是阻碍发展的瓶颈。
工作了几年就会发现,技术框架更新迭代非常快,框架是学不完的,但是框架的底层原理都是相同的,都是由基础衍生出来的,今天我继续之前的学习算法之路来看看基本功中排序算法的堆排序、二叉树的遍历与生产者消费者模型。
-
堆排序
堆积排序(Heapsort)是指利用堆积树(堆)这种数据结构所设计的一种排序算法,可以利用数组的特点快速定位指定索引的元素。
堆排序是不稳定的排序方法,辅助空间为O(1), 最坏时间复杂度为O(nlog2n) ,堆排序的堆序的平均性能较接近于最坏性能。
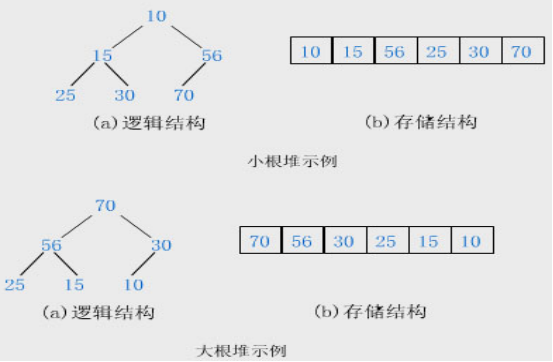
堆排序利用了大根堆(或小根堆)堆顶记录的关键字最大(或最小)这一特征,使得在当前无序区中选取最大(或最小)关键字的记录变得简单。
-
用大根堆排序的基本思想
-
先将初始文件 R[1..n] 建成一个大根堆,此堆为初始的无序区
-
再将关键字最大的记录 R[1] (即堆顶)和无序区的最后一个记录 R[n] 交换,由此得到新的无序区 R[1..n-1] 和有序区 R[n] ,且满足 R[1..n-1].keys≤R[n].key
-
由于交换后新的根 R[1] 可能违反堆性质,故应将当前无序区 R[1..n-1] 调整为堆。然后再次将 R[1..n-1] 中关键字最大的记录 R[1] 和该区间的最后一个记录 R[n-1] 交换,由此得到新的无序区 R[1..n-2] 和有序区 R[n-1..n],且仍满足关系 R[1..n-2].keys ≤ R[n-1..n].keys,同样要将R[1..n-2]调整为堆。如此循环……
-
直到无序区只有一个元素为止。
-
大根堆排序算法的基本操作:
-
初始化操作:将 R[1..n] 构造为初始堆;
-
每一趟排序的基本操作:将当前无序区的堆顶记录 R[1] 和该区间的最后一个记录交换,然后将新的无序区调整为堆(亦称重建堆)。
注意:
-
只需做n-1趟排序,选出较大的 n-1 个关键字即可以使得文件递增有序。
-
用小根堆排序与利用大根堆类似,只不过其排序结果是递减有序的。堆排序和直接选择排序相反:在任何时刻堆排序中无序区总是在有序区之前,且有序区是在原向量的尾部由后往前逐步扩大至整个向量为止。
public class HeapSortTest { public static void main(String[] args) { int[] data5 = new int[] { 5, 3, 6, 2, 1, 9, 4, 8, 7 }; print(data5); heapSort(data5); System.out.println("排序后的数组:"); print(data5); } //交换数组位置 public static void swap(int[] data, int i, int j) { if (i == j) { return; } data[i] = data[i] + data[j]; data[j] = data[i] - data[j]; data[i] = data[i] - data[j]; } //堆排序调用 public static void heapSort(int[] data) { for (int i = 0; i < data.length; i++) { createMaxdHeap(data, data.length - 1 - i); swap(data, 0, data.length - 1 - i); print(data); } } //创建最大堆 public static void createMaxdHeap(int[] data, int lastIndex) { for (int i = (lastIndex - 1) / 2; i >= 0; i--) { // 保存当前正在判断的节点 int k = i; // 若当前节点的子节点存在 while (2 * k + 1 <= lastIndex) { // biggerIndex总是记录较大节点的值,先赋值为当前判断节点的左子节点 int biggerIndex = 2 * k + 1; if (biggerIndex < lastIndex) { // 若右子节点存在,否则此时biggerIndex应该等于 lastIndex if (data[biggerIndex] < data[biggerIndex + 1]) { // 若右子节点值比左子节点值大,则biggerIndex记录的是右子节点的值 biggerIndex++; } } if (data[k] < data[biggerIndex]) { // 若当前节点值比子节点最大值小,则交换2者得值,交换后将biggerIndex值赋值给k swap(data, k, biggerIndex); k = biggerIndex; } else { break; } } } } public static void print(int[] data) { for (int i = 0; i < data.length; i++) { System.out.print(data[i] + "\t"); } System.out.println(); } }
public class HeapSortTest {public static void main(String[] args) {int[] data5 = new int[] { 5, 3, 6, 2, 1, 9, 4, 8, 7 };print(data5);heapSort(data5);System.out.println("排序后的数组:");print(data5);}//交换数组位置public static void swap(int[] data, int i, int j) {if (i == j) {return;}data[i] = data[i] + data[j];data[j] = data[i] - data[j];data[i] = data[i] - data[j];}//堆排序调用public static void heapSort(int[] data) {for (int i = 0; i < data.length; i++) {createMaxdHeap(data, data.length - 1 - i);swap(data, 0, data.length - 1 - i);print(data);}}//创建最大堆public static void createMaxdHeap(int[] data, int lastIndex) {for (int i = (lastIndex - 1) / 2; i >= 0; i--) {// 保存当前正在判断的节点int k = i;// 若当前节点的子节点存在while (2 * k + 1 <= lastIndex) {// biggerIndex总是记录较大节点的值,先赋值为当前判断节点的左子节点int biggerIndex = 2 * k + 1;if (biggerIndex < lastIndex) {// 若右子节点存在,否则此时biggerIndex应该等于 lastIndexif (data[biggerIndex] < data[biggerIndex + 1]) {// 若右子节点值比左子节点值大,则biggerIndex记录的是右子节点的值biggerIndex++;}}if (data[k] < data[biggerIndex]) {// 若当前节点值比子节点最大值小,则交换2者得值,交换后将biggerIndex值赋值给kswap(data, k, biggerIndex);k = biggerIndex;} else {break;}}}}public static void print(int[] data) {for (int i = 0; i < data.length; i++) {System.out.print(data[i] + "\t");}System.out.println();}}
-
树的遍历(深度优先、广度优先)
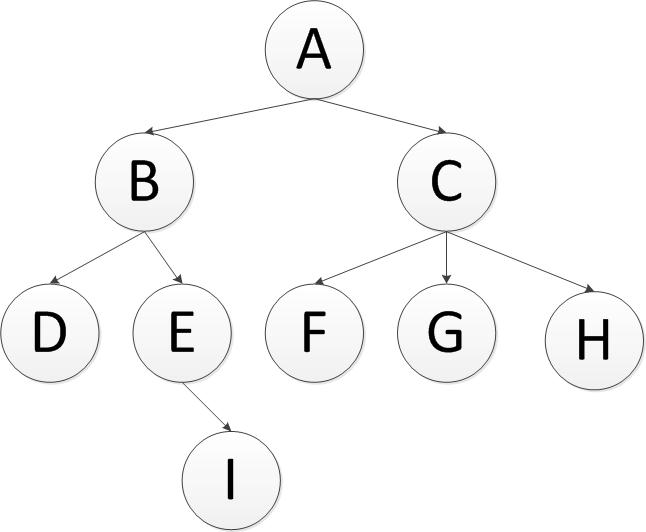
在编程生活中,我们总会遇见树性结构,这几天刚好需要对树形结构操作,就记录下自己的操作方式以及过程。现在假设有一颗这样树,(是不是二叉树都没关系,原理都是一样的)
深度优先
英文缩写为 DFS 即 Depth First Search.其过程简要来说是对每一个可能的分支路径深入到不能再深入为止,而且每个节点只能访问一次。对于上面的例子来说深度优先遍历的结果就是:A,B,D,E,I,C,F,G,H.(假设先走子节点的的左侧)。
深度优先遍历各个节点,需要使用到堆(Stack)这种数据结构。Stack的特点是是先进后出。
整个遍历过程如下:
-
首先将A节点压入堆中,stack(A);
-
将A节点弹出,同时将A的子节点C,B压入堆中,此时B在堆的顶部,stack(B,C);
-
将B节点弹出,同时将B的子节点E,D压入堆中,此时D在堆的顶部,stack(D,E,C);
-
将D节点弹出,没有子节点压入,此时E在堆的顶部,stack(E,C);
-
将E节点弹出,同时将E的子节点I压入,stack(I,C);
-
...依次往下,最终遍历完成。Java 代码如下:
public void depthFirst() { Stack<Map<String, Object>> nodeStack = new Stack<Map<String, Object>>(); //节点使用Map存放 Map<String, Object> node = new HashMap<String, Object>(); nodeStack.add(node); while (!nodeStack.isEmpty()) { node = nodeStack.pop(); System.out.println(node); //获得节点的子节点,对于二叉树就是获得节点的左子结点和右子节点 List<Map<String, Object>> children = getChildren(node); if (children != null && !children.isEmpty()) { for (Map child : children) { nodeStack.push(child); } } } }
广度优先
英文缩写为 BFS 即 Breadth FirstSearch。其过程检验来说是对每一层节点依次访问,访问完一层进入下一层,而且每个节点只能访问一次。对于上面的例子来说,广度优先遍历的 结果是:A,B,C,D,E,F,G,H,I(假设每层节点从左到右访问)。
广度优先遍历各个节点,需要使用到队列(Queue)这种数据结构,
Queue 的特点是先进先出,其实也可以使用双端队列,区别就是双端队列首位都可以插入和弹出节点。整个遍历过程如下:
-
首先将A节点插入队列中,queue(A);
-
将A节点弹出,同时将A的子节点B,C插入队列中,此时B在队列首,C在队列尾部,queue(B,C);
-
将B节点弹出,同时将B的子节点D,E插入队列中,此时C在队列首,E在队列尾部,queue(C,D,E);
-
将C节点弹出,同时将C的子节点F,G,H插入队列中,此时D在队列首,H在队列尾部,queue(D,E,F,G,H);
-
将D节点弹出,D没有子节点,此时E在队列首,H在队列尾部,queue(E,F,G,H);
-
...依次往下,最终遍历完成,Java 代码如下:
public void breadthFirst() { //这里使用的是双端队列,和使用queue是一样的 Deque<Map<String, Object>> nodeDeque = new ArrayDeque<Map<String, Object>>(); Map<String, Object> node = new HashMap<String, Object>(); nodeDeque.add(node); while (!nodeDeque.isEmpty()) { node = nodeDeque.peekFirst(); System.out.println(node); //获得节点的子节点,对于二叉树就是获得节点的左子结点和右子节点 List<Map<String, Object>> children = getChildren(node); if (children != null && !children.isEmpty()) { for (Map child : children) { nodeDeque.add(child); } } } }
-
生产者消费者模型
重点使用 BlockingQueue,它也是 java.util.concurrent 下的主要用来控制线程同步的工具。
BlockingQueue 有四个具体的实现类,根据不同需求,选择不同的实现类
1)ArrayBlockingQueue:一个由数组支持的有界阻塞队列,规定大小的 BlockingQueue,其构造函数必须带一个 int 参数来指明其大小.其所含的对象是以 FIFO (先入先出)顺序排序的。
2)LinkedBlockingQueue:大小不定的 BlockingQueue,若其构造函数带一个规定大小的参数,生成的BlockingQueue有大小限制,若不带大小参数,所生成的 BlockingQueue 的大小由Integer.MAX_VALUE来决定.其所含的对象是以 FIFO (先入先出)顺序排序的。
LinkedBlockingQueue 可以指定容量,也可以不指定,不指定的话,默认最大是Integer.MAX_VALUE,其中主要用到 put 和take方法,put 方法在队列满的时候会阻塞直到有队列成员被消费,take 方法在队列空的时候会阻塞,直到有队列成员被放进来。
3)PriorityBlockingQueue:类似于LinkedBlockQueue,但其所含对象的排序不是FIFO,而是依据对象的自然排序顺序或者是构造函数的Comparator 决定的顺序。
4)SynchronousQueue:特殊的 BlockingQueue,对其的操作必须是放和取交替完成的。
//生产者: import java.util.concurrent.BlockingQueue; public class Producer implements Runnable { BlockingQueue<String> queue; public Producer(BlockingQueue<String> queue) { this.queue = queue; } @Override public void run() { try { String temp = "A Product, 生产线程:" + Thread.currentThread().getName(); System.out.println("I have made a product:" + Thread.currentThread().getName()); //如果队列是满的话,会阻塞当前线程 queue.put(temp); } catch (InterruptedException e) { e.printStackTrace(); } } } //消费者: import java.util.concurrent.BlockingQueue; public class Consumer implements Runnable{ BlockingQueue<String> queue; public Consumer(BlockingQueue<String> queue){ this.queue = queue; } @Override public void run() { try { //如果队列为空,会阻塞当前线程 String temp = queue.take(); System.out.println(temp); } catch (InterruptedException e) { e.printStackTrace(); } } } //测试类: import java.util.concurrent.ArrayBlockingQueue; import java.util.concurrent.BlockingQueue; import java.util.concurrent.LinkedBlockingQueue; public class Test3 { public static void main(String[] args) { BlockingQueue<String> queue = new LinkedBlockingQueue<String>(2); // BlockingQueue<String> queue = new LinkedBlockingQueue<String>(); //不设置的话,LinkedBlockingQueue默认大小为Integer.MAX_VALUE // BlockingQueue<String> queue = new ArrayBlockingQueue<String>(2); Consumer consumer = new Consumer(queue); Producer producer = new Producer(queue); for (int i = 0; i < 5; i++) { new Thread(producer, "Producer" + (i + 1)).start(); new Thread(consumer, "Consumer" + (i + 1)).start(); } } }
由于队列的大小限定成了 2,所以最多只有两个产品被加入到队列当中,而且消费者取到产品的顺序也是按照生产的先后顺序,原因就是LinkedBlockingQueue 和 ArrayBlockingQueue 都是按照 FIFO 的顺序存取元素的。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号