求pi方法总结

 

 

 

古今中外，求Pi的方法主要有三类主要的方法：

1，正多边形逼近法

2，迭代法（级数法）

3，蒙特卡洛法（随机模拟）

方法一不便用程序实现，方法二和三均可用程序语言实现，实现方法如下：

方法二（迭代法）：

//求pi 使用迭代法 pi/4=1-1/3+1/5-1/7+1/9-。。。
#include<stdio.h>
#include<math.h>
int main(int argc, char const *argv[])
{
    double PI=0,term=1,n=1;
    int sign=1;
    while(fabs(term)>=pow(10,-6)){
        PI+=term;
        n=n+2;
        sign=-sign;
        term=sign/n;
    }
    printf("PI=%10.8f\n",PI*4);
    return 0;
}

//求pi，使用迭代法 pi/2=1+1/3+(1/3)*(2/5)+(1/3)*(2/5)*(3/7)+...
//An=An-1*((n-1)/(2*n-1))
#include<stdio.h>
#include<math.h>
int main(int argc, char const *argv[])
{
    double PI=0,term=1,n=1;
    while(fabs(term)>=pow(10,-6)){
        PI+=term;
        n++;
        term=term*((n-1)/(2*n-1));
    }
    PI=PI*2;
    printf("PI=%10.8f\n",PI);
    return 0;
}

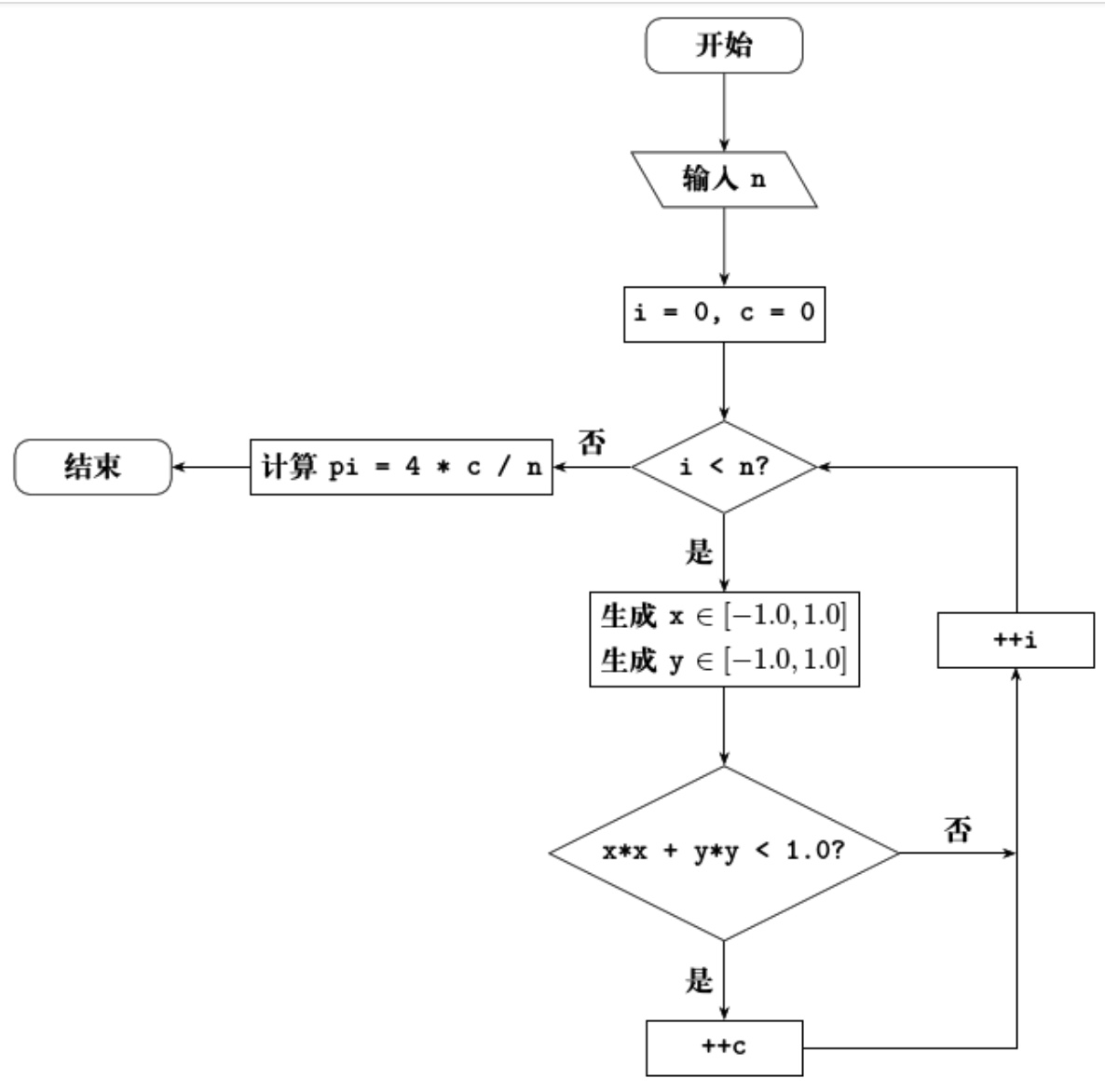
方法三（蒙特卡洛方法）【参考《算法与程序设计》一书】：

//求pi，使用蒙特卡洛法，使用随机模拟结果统计来求得pi的近似值
#include<stdio.h>
#include<stdlib.h>
#include<time.h>
int main(int argc, char const *argv[])
{
    double n,c=0;
    //srand声明在stdlib.h，time声明在time.h
    //srand作用使用当前时间作为随机数发生器的种子值
    srand(time(0));
    scanf("%lf",&n);
    for (int i = 0; i <=n; ++i)
    {
      //RAND_MAX定义在stdlib.h中，代表rand函数返回的最大值
      //rand函数定义在stdlib.h中
        double x=-1.0+2.0*rand()/RAND_MAX;
        double y=-1.0+2.0*rand()/RAND_MAX;
        if (x*x+y*y<1.0)
        {
            ++c;
        }
    }
    double PI=(4*c)/n;
    printf("%f\n",PI);
    return 0;
}