[摘抄]读懂MTF曲线(How to Read MTF Curves)
前言
光学的规则是复杂且令人讨厌的。
这句话来源于一场互联网上关于 “如何阅读 MTF 曲线” 的讨论。这个句子很好地,并坦诚地告诉了我们:对于摄影师来说,理解这个充满数字的世界是如何的困难。
不过,我将在接下来的内容里向您展示,其实事情并没有这么糟糕。您并不需要学习傅立叶光学中的高等数学即可理解其中的基本关系。
读完这篇文章后,您将能够通过阅读一个镜头制造商或者测试机构所提供的 MTF 数据来总结一枚镜头的特性。但与此同时,您也将了解到 MTF 的局限性,以便您批判性地阅读镜头的评测。
对于一些认为摄影主要是基于经验的人来说,看完这篇文章可能会更加确信:如此繁多的数字和曲线并非优秀的摄影所需的。但更好地了解您的工具这件事情本身是充满着极大乐趣的,这也是我希望的您在阅读这第一部分的过程所能收获的东西。而在第二个部分中,我们将向您展示一些说明图像。
点扩散函数(Point Spread Function)
当摄影师想要对一个对象拍摄一张看起来非常自然的图片的时候,他们会希望相机上有一个“理想的镜头”。理想的镜头拥有这样的特征:让从物体某个点发出的所有的光线再次在图像的一个点上再次相遇。然而我们现在知道,使用真实的镜头时,只能部分实现这一理想的目标。现实中并不存在几何学意义上的“图像点”。(译者注:在几何学上,一个点是没有大小的。)
源自物体一个点的光会始终分布在围绕那个理想的 “图像点” 周围的区域内,这是因为透镜系统的像差,制造工差,以及光呈现出来的波的特性等因素共同决定的。
某种程度上来说,这一区域就是 “最小的弥散圆(Circle of Confusion)”。不过由于汇聚的光在这个区域内并非均匀分布的——一般来说光的强度从内向外减小,并且这一区域的形状很少呈现圆形。
这种效应被称为 点扩散函数”(Point Spread Function),它的形状和大小就代表了这个镜头所成图像质量的特征。
如果将摄影比作绘画,那么点扩散函数就是笔迹,即镜头的笔触。就像绘画中有宽的、扁平的、尖头的、或者毛刷一样,镜头也有不同的笔迹风格。

但为什么它仍然没有被用作描述图像质量的量化标准呢?
主要有以下的三点原因:
首先,点扩散函数的形状往往是非常复杂的,无法简单地用一个数字来描述。在以下这些照片里,我们将使用一台显微镜拍摄的照片来说明这一点。图像 1-6 中的点扩散都是可用,但质量一般的范例,这类点扩散是非常典型的,它们往往出现在高速镜头(译者注:大光圈镜头)光圈全开时,或者是出现在广角镜头的图像边缘,或者是出现在轻微失焦的时候。
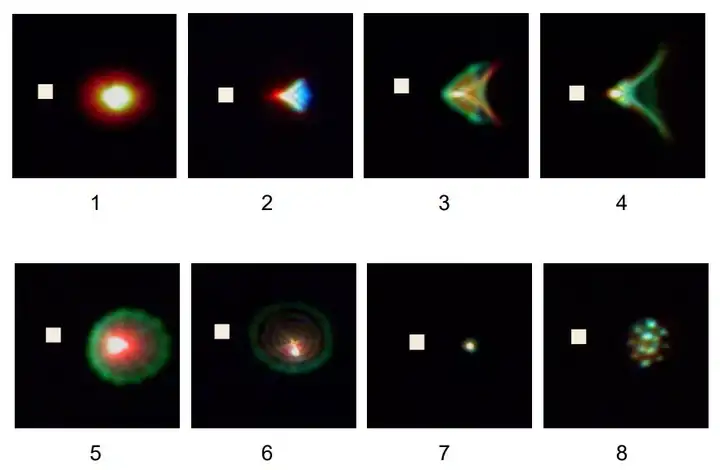 点扩散函数的范例
点扩散函数的范例
为了方便比对大小,我们在图片里粘贴了一个白色的正方形,它代表一个边长 8.5μm 的像素,和全画幅 1200 万像素相机的像素一样大。很明显,这些点扩散都明显地比这个像素尺寸大。
上图第二行中的 7 号图像所展示的点扩散是一个代表出色成像性能的例子。然而,数字传感器(因为低通滤波器的存在)通常不会看到如此小的点扩散。最右侧的 8 号图像显示了低通滤波器后面的同一个点。低通滤波器旨在抑制摩尔效应,通常位于传感器前方。因此,低通滤波器后的图像质量会被人为地恶化。通过数个双折射碟后点扩散的大小会显著地增加。
第二个原因是你几乎永远不会看到这样一个孤立的点扩散。例如:只有在漆黑的夜晚拍摄星星时,才能达到与实验室相同的效果。大多数图像是在相机中以复杂的方式去组合无数独立的点扩散而生成的。
这是因为物体的一小部分也由许多密集的点组成,这些点对应于镜头后面图像中的许多密集的理想图像点。由于实际点扩散并不是无限小的,这就意味着独立的点扩散会重叠:图像的一个点处的强度(甚至可以说在一个像素中)是通过对许多的点扩散进行二维积分(求和)生成的。因此,在镜头的“笔画”和我们所见的最终图像之间有一个并不那么容易归纳的数学关系。
第三个原因是从镜头到肉眼的成像链(imaging chain)可以被一个更加优雅的方式所描述,我现在将对这个方法进行解释。
调制传递(Modulation Transfer)
与星星不同,一个连续的物体(Extended Object)包含无限多的点。由于我们主要关注连续的物体是如何进行成像的,因此我们必须找到另一种定量描述图像质量的方法。我们使用正弦亮度分布(sinusoidal brightness distribution)来测试一个看起来尽可能简单的对象是如何被成像的。
一个正弦亮度分布是亮条纹和暗条纹相间的图案,其中亮和暗之间的过渡逐渐且连续地发生,在此处,我们使用正弦的关系,就像我们的插座中的电功率随时间变化而变化那样。我们使用正弦条纹图案是因为无论点扩散的形状有多复杂,它所成的像依旧是正弦图案。
它的一些属性也仍然保持稳定——或至少与成像质量无关:条纹的方向不会改变、而且条纹的频率 - 即每单位长度条纹的数量 - 仅根据成像的放大率(imaging scale)变化。
然而,暗条纹和亮条纹之间的亮度差异不再与原始正弦图像相同。这是因为连续的点扩展确保部分光线落在实际上完全黑暗的位置,而不是落在明亮的位置。
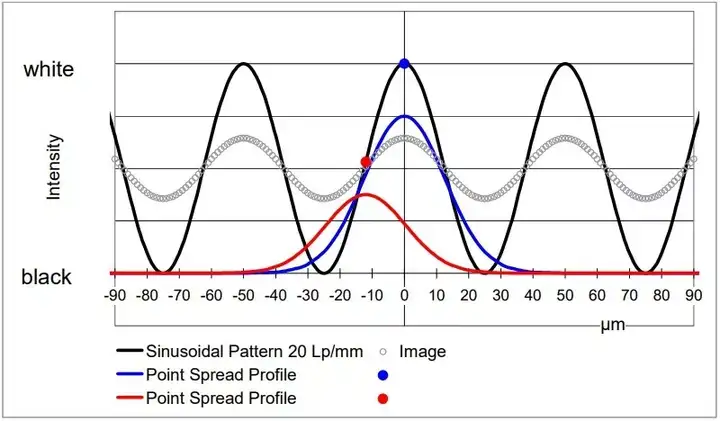
该图显示了一个亮度(垂直于条纹的方向上的截面)随正弦波规律变化的条纹图案(黑色曲线)。它每毫米有 20 个周期,因此一个周期为 50 微米长。红色和蓝色曲线是一个点扩散中亮度分布的横截面。在蓝点处,理想的成像点周围的亮度分布将会遵循蓝色曲线。因此,您可以看到一些光线落入蓝点旁边 25μm 处暗处的波谷中(译者注:在 ±25μm 处,黑色曲线处于波谷,亮度为 0,即纯黑)。
这个波谷同时也会接收到来自旁边红点标记处的光。虽然红点处的的正弦图案较暗,但由于红点离波谷较蓝点更近,所以会有较多一部分的光达到 -25μm 的波谷处。因此,图案的暗区域中的亮度是来自相邻区域的许多相似贡献的总和。这一现象的结果就是标记为“图像”的、起伏较小的调制曲线(modulation curve,图像调制曲线在图中用白点标注)。图像中暗条纹的亮度由像差提高,而亮条纹变暗。
在光学中,亮与暗之间的差异被称为“对比度”(Contrast)。从更通用的角度来看,所有遵循正弦规律,周期性变化量的最大值和最小值之间的差异都可以被称为“调制”(Modulation)。如果我们简单地将图像的调制除以物体的调制,我们就能得到一个描述镜头成像性质的一个数字:调制传递(Modulation Transfer)。到此,我们已经理解了术语 “MTF” 的前两个字母。它是一个 0 到 1 之间,或者说 0 到 100% 之间的数字(译者注:由于图像的调制小于等于物体的调制,所以两者的商始终处于 0 到 1 之间)。
摄影师们习惯于用光圈档位描述明暗差异,这也是非常合理的,因为人眼对亮度的感知是遵循对数尺度的。但,如果我们的亮暗区别是 6 档(最暗和最亮的地方比例是 1:2^6,也就是 1:64),而调制传递是 50%,这代表了什么呢?是说图像的调制最亮和最暗的地方差别是 3 档,还是说 1:64/2,也就是 1:32 (也就是 5 档)呢?其实这两个答案都是错误的,现实中,我们大概会有 1.5 档光圈的差距。这是因为在光学里,对比度被定义为 “最大值与最小值的差除以最大值和最小值的和”。
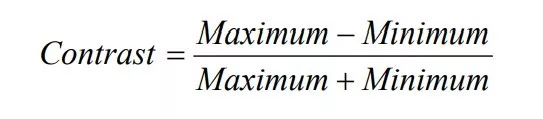
因此,在上面的例子里,物体的对比度是 63/65,约等于 0.97,而成像后,由于调制传递是 50%,对比度只有一半,约 0.48,最小值和最大值的比例大约是 1:2.9(1.9/3.9=0.48)。
下图展示了如果使用光圈档位测量的话,物体对比度与图像对比度在不同的调制传输下的关系。
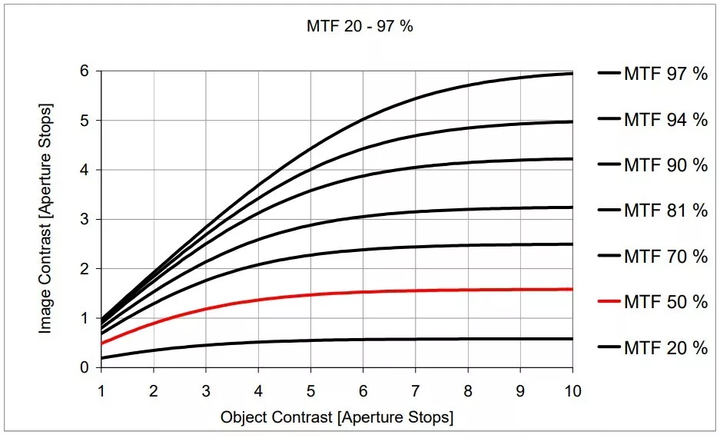
我们可以认识到 MTF 的三个重要性质,这也是我们在阅读 MTF 曲线时需要注意的:
其一,当物体对比度高时,较高 MTF 数值的微小差异也是非常显著的。(译者注:当 Object Contrast 较高时,MTF 94% 到 97% 的差异也是显著的,尽管 MTF 值只提高了 3 个百分点,可从图右侧看出)
其二,小于一档光圈的弱影调差异变化,并不需要较高的 MTF 值,高于 MTF 70-80% 的区别几乎是无关的。(译者注:当 Object Contrast 为 1 时,MTF 70% - 97% 的值差异很小,可从图左侧密集的曲线看出)
其三,在非常低的 MTF 值下,物体的对比度高低并不重要,无论物体对比度多高,图像的对比度一直是很低的。(译者注:这可以从平坦的 MTF 20% 曲线看出,Image Contrast 的变化并不显著)
顺便一提,这就是为什么胶片的数据表总是给出在 1∶1.6 的低对比度下的分辨力的原因。在 1∶1000 对比度下的分辨力只能由接触式曝光(Contact Exposure)测得。对于最精细的细节(例如非常高的空间频率),世界上没有任何镜头能够产生十挡光圈的对比度。因此,基于较高分辨力数值去估计图像的信息量是过于乐观的。(译者注:即 1∶1000 的对比度下,以富士 Provia 100F Professional 胶片为例,官方给出 1∶1.6 下分辨力为 60 线每毫米,而 1∶1000 下为 140 线每毫米)
附:富士 Provia 100F Professional 的参数表
调制传递函数,分辨力(Modulation transfer function, resolving power)
很明显,单个条纹图案很显然不足以反映一个镜头的素质。一个非常粗糙的、明暗间隔非常大的图像显然也可以被一个点扩散函数非常松散的镜头所很好的呈现。但如果我们缩小条纹之间的距离,使其接近于点扩散的大小,那么大量来自于较亮区域的光就会落在图案的较暗的区域,图像的对比度也随之下降。
我们可以再次用笔刷做类比:不那么精细的画面,用较粗的画笔就可以绘制得很好,但是那些很细的画笔,是为了画面的细节所准备的。
因此,我们需要探寻镜头如何呈现不同精细程度的条纹图案,例如,对于这些不同的图案,我们需要确定每一个的调制传递(Modulation Transfer)。我们会获得一系列的值,如果我们将其作为因变量,以某一形容条纹图案精细度的参数为自变量,那么会得到一个函数——调制传递函数(Modulation Transfer Function)。
条纹图案的精细程度可以用图像中一毫米内包含多少个周期来形容。一个周期就是指相邻的两个两条纹或者暗条纹之间的片段,或者包含一个暗条纹和一个亮条纹的线对的宽度。在像平面上每毫米之中包含的周期数称为空间频率(Spatial Frequency),单位是线对每毫米,缩写为 lp/mm。
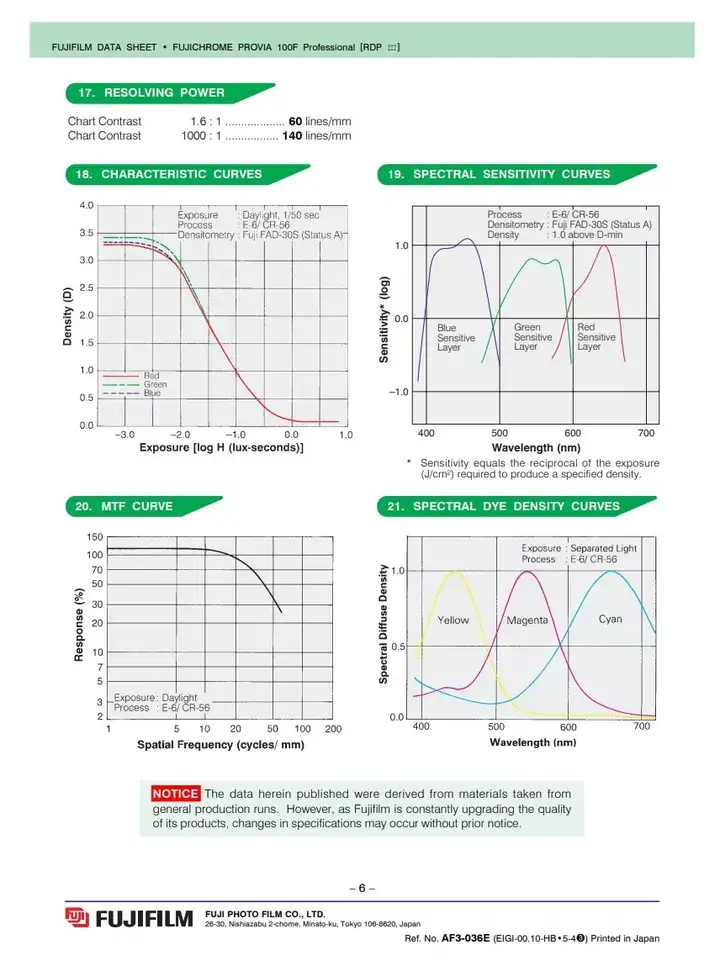
图片展示了一个 35mm 格式(全画幅)的 50mm 镜头中心的调制传递函数,两组数据分别是在光圈为 f/2 和 f/5.6 时测得的。为了便于比较,衍射极限所限制的调制传递函数(diffraction-limited transfer functions)用没有圆点的实线画出。衍射极限代表着最理想的图像。而在横轴上,我们使用 lp/mm 来测量空间频率。
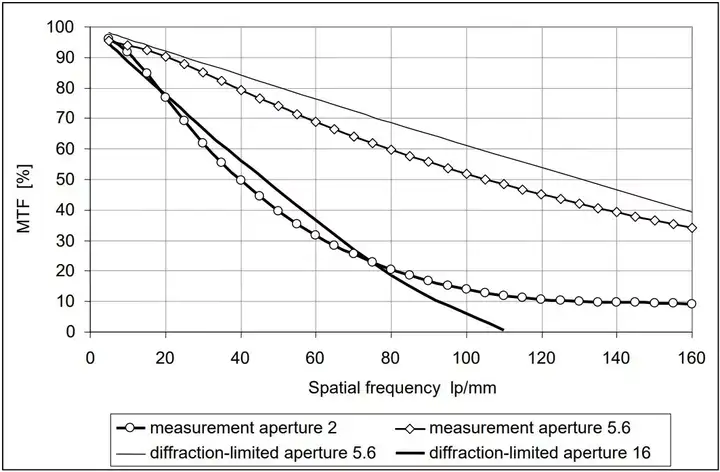
一个衍射极限的图像有一条几乎是直线的 MTF 曲线,随着空间频率的增加而按比例减少。MTF 0 的值在所谓的“截止频率”(limit frequency)出现,截止频率由光圈大小(f number)和光的波长共同决定。
一个对中等波长的可见光的估测是:点扩散的宽度(μm)和 f number 数值上一致,而截止频率约等于 1500 除以 f number。
对于真实的镜头而言,其 MTF 曲线会在一开始快速下降,而后非常缓慢地趋近于零,因此曲线会出现下垂。这一点在图中光圈值为 f/2 的曲线上十分明显,而光圈值为 f/5.6 的镜头则与物理上的最佳的理想镜头相差不会太远。
当 MTF 值为零或低于一个阈值(例如10%)时,对应的空间频率就是镜头在空气中的分辨力。低于这个频率的条纹图案可以被很好地呈现,而不是变成失去细节的一片灰色。
分辨力的极限是难以测量的,图中光圈值为二的 MTF 曲线可以很典型地说明这一问题:在高空间频率下,其曲线非常平坦,很小的 MTF 值范围对应着很大的空间频率范围,这意味着最终的结果会高度敏感地依赖于你所要求的最小对比度。因此,测量结果将会非常不精确的。由于这一原因,在空气中的分辨力并不能作为一个合格的镜头质量指标。
注意请不要把上面所说的分辨力与经由感光元件所获得的分辨力混淆。这就引出了我们上面提到的要使用调制函数(modulation function)描述图像质量的第三个原因:
我们要想观察图像从来不只依赖于镜头,而是需要其他更多的设备加入成像链(imaging chain):我们总是需要一个图像传感器,无论是数码的还是银盐的,此外还可能是一个扫描仪,一个印刷机或者是一个投影镜头。
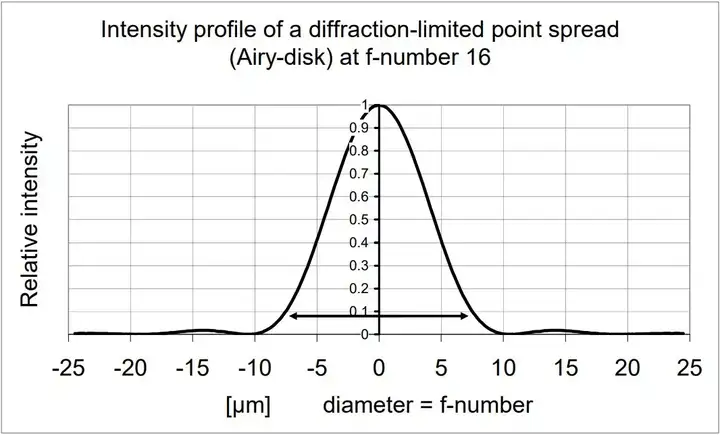
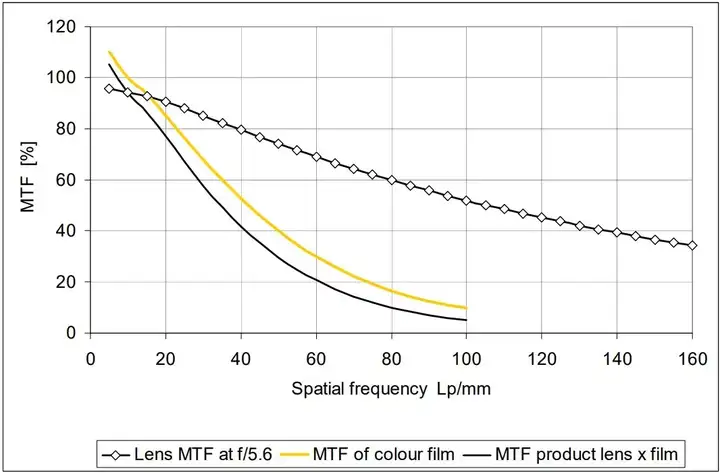
所有这些元件,甚至我们的肉眼,都有其自己的成像特性,也都可以用传递函数描述。而 MTF 的优点在于,这一串元件构成的成像链的总 MTF 值,约等于每一个独立元件 MTF 值的乘积。下面让我们来看一看一些典型的例子:
两个 MTF 的乘积:非常好的 135 镜头和彩负胶片。两者的乘积总是小于最小的那个因子。
在这个例子中,总的调制函数被基本上是被胶片所限制。如果选定 10% 为最低值,那么我们应该预期得到 80-100lp/mm 的分辨力。如果同时把投影设备或者我们的肉眼加入计算,那么最终的乘积还会略低一些。
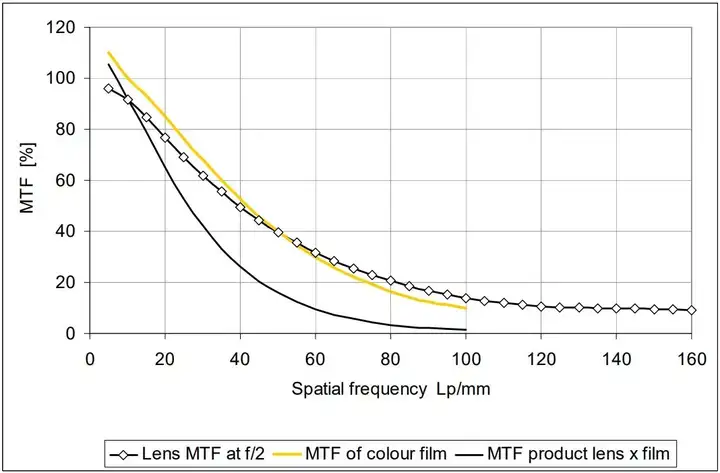
两个 MTF 的乘积:135 镜头和中等性能的彩负胶片。二者对乘积的贡献几乎完全相同。
在只计算两个调制函数的乘积时,我们就能清楚的看到,去考查完整的高空间频率的 MTF 并不是必要的。更不必说实际情况下会有更多的元件参与这一过程,从而使得 MTF 值愈发的低。
2400 万像素的全画幅数码传感器或是 1500 万像素的 APS-C 画幅传感器,对应了大约 90lp/mm 的奈奎斯特频率。因此在理论上它们具有与彩负胶片相当的分辨力。也就是考察 40lp/mm 的空间频率就足够了。而对于更高像素的传感器来说,40lp/mm 的指标会显得更加重要。
从另一个角度考虑,这个限制(指 40lp/mm)也是合理的:如果一个人在 25m 的 “明视最短距离” 上观看一张 A4 大小的印刷物,这张印刷物大约会占据 60° 的视角,在这个距离上人眼上最高的解析力为 8lp/mm,所以对图像的解析力为 1600lp/图像。对于一个高度为 24mm 全画幅的格式来说,这对应 66lp/mm,因此,对人眼来说有意义的空间频率也就大概在 40lp/mm 这个范围。
如果一个人将图像显著放大,而还在较短的距离上观看它的话,眼睛就能利用整个系统中最高的空间频率看到在普通情况下看不到的图像缺陷。这和人们在大尺寸屏幕上以 100% 的模式观看数字图像时发生的事情是一致的,在这种情况下,一张 1200 万像素的照片会超过 1 米长。
顺带一提,低感光度的黑白胶片能够利用镜头在高频的性能表现。
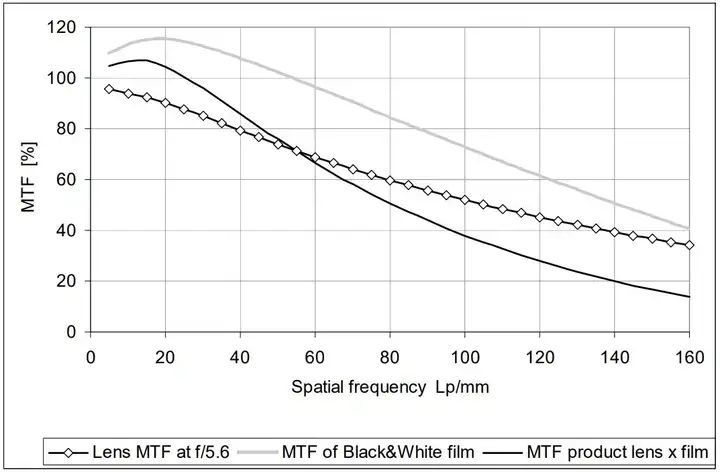
好镜头搭配高分辨率黑白胶片(数据来源于 T-Max 100)
下图展示了对于全画幅格式来说,40lp/mm 已经是一个挺高的空间频率了。

这里展示了著名的西门子星(Siemens Star)图案,这一图案被广泛应用于相机测试中。完整的图片里展示了全画幅相机拍摄的 1200 万像素的图片里有着 9 颗星。

一个大比例放大的局部图片里展示了 40lp/mm 离西门子星的中心有多近。
原文:2008 年 12 月,蔡司相机镜头分部,H. H. Nasse 的文章 How to Read MTF Curves
首发于公众号:字节社。
翻译:字节君,同时感谢 ProcrastinatorC 的大力相助。

 浙公网安备 33010602011771号
浙公网安备 33010602011771号