[摘抄]浅析鱼眼镜头

1 从针孔到凸透镜

从几万年前的原始人类开始，人们就一直想要把看到的景象记录下来。最开始在岩石上用矿物粉末作画，后来在纸、布上用笔墨作画。在很长一段时间内，人们总是在追求描摹得更真实，在这个过程中，人们逐渐学习到了各种光学现象，总结出很多光学的规律，并将之应用于实践，于是制造出了最早的相机——针孔相机。

针孔相机是利用小孔成像原理，将外部的景物经由小孔，成像在相机的成像平面上（有关针孔相机的一些详细计算和有趣讨论，参见之前的专栏文章《针孔相机与昆虫复眼》）。在一开始甚至没有用于记录影像的材料，人们便在这个成像平面上依照影像来作画，来描摹出更真实的场景。（图片来自 WiKi Camera obscura）

（使用针孔相机进行描摹）

针孔相机的针孔，就可以看做最早的镜头了，可惜这个「镜头」性能实在不能满足要求。针孔相机若要成像清晰，针孔的大小就必然不大（参见之前文章中的计算和讨论），经由针孔进入相机的光线也是少的可怜；即使如此，在成像平面上的像也不是那么清晰。直到后来，人类发明了凸透镜，利用凸透镜成像，取代小孔，成为相机真正意义上的镜头。凸透镜做镜头有着显而易见的好处。凸透镜可以做得比小孔大的多，从而进入相机的光线也多的多，落在相机成像平面上的像自然也明亮的多了。此外凸透镜成像的清晰度可比小孔要高多了，而且不会明显受到透镜大小的影响。（图片来自 WiKi Camera obscura）

（使用凸透镜（镜头）进行描摹）

用凸透镜做镜头，尽管形式改了，但是成像投影的方式并没有变化，都可以用同样的数学来进行描述。所以，现在很多计算机图形学中，对相机的简单建模，仍然用针孔相机来表示。在这个简单的「针孔相机」模型中，像与物之间是「相似」的，或者更严格地用数学语言来说，像与物之间是经过了「射影变换（Perspective Transform）」（在以前的专栏文章《移轴摄影、沙姆定律与射影几何》和《星野摄影降噪（2）：对齐叠加》中都有提到射影变换），在射影变换下，像与物之间保持了某些相似的特性，比如直线经过变换仍然是直线，圆锥曲线（比如椭圆）经过变换仍然是圆锥曲线，两直线的交点经过变换仍然是两直线相交的点，直线的交比经过变换保持不变，等等。正因为射影变换保持了很多几何性质不变，所以我们看照片，是能够与原场景联系起来的，照片与原场景之间存在某些相似性。

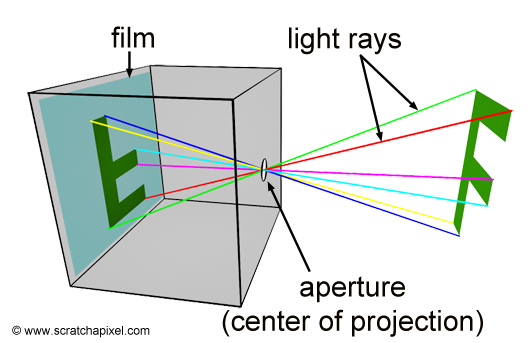
（针孔相机模型）

从这个角度来看，相机镜头起的作用，就是做了一个数学变换，把物空间变换成了像空间，然后成像平面在这个像空间内切了一刀，截取了一个平面，成为拍下的照片。在不同场合下，许多称呼包括普通镜头（Normal lens）、射影镜头（Perspective lens）、线性镜头（Linear lens）、针孔相机模型（Pinhole camera model）等，均指代这种，遵从射影变换的相机 / 镜头模型。（图片来自 Scratchapixel）

2 鱼眼与鱼眼镜头

对日常生活、甚至一些艺术创作、科学研究来说，保持像与物的相似是一件好事。偏离相似性，我们就说镜头有了畸变，大多数时候，我们并不希望镜头有畸变，甚至在设计镜头的时候，专门针对「偏离相似性」——也就是镜头畸变进行校正。不过在一些特殊的场合，我们也需要特意偏离物像的相似性，以求得其他方面的便利。

一个极好的例子是气象科学中，对天空云量的测量。在这个场景中，人们希望能够获得尽可能大的视野范围，最好是直接把整个天空一次性拍摄下来——这就要求镜头能够达到 180° 的视场角。容易想到，我们可以把天空和云看做分布于一个半径无穷大的球面上，也就是说，我们要把一个（半）球面的场景尽可能全地记录、拍摄下来。普通的超广角镜头难以完成这样的任务。

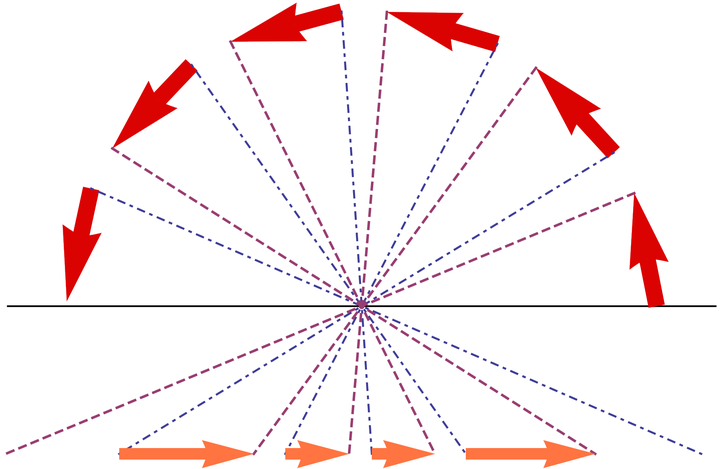
（普通镜头无法记录完整的半球场景）

如图所示，面对半球场景，普通的超广角镜头只能记录中间的部分，越靠近边缘，透视变形越大。图中同样长度的红色箭头，靠近边缘的话，经过镜头成像之后就变得更长；对于极端接近边缘的物体，普通的广角镜头是无法成像记录的。这种情况下，追求「相似性」反而成为了障碍。

既然追求「相似性」的普通镜头难以胜任这样的任务场景，那么我们放弃相似性是不是就可以完成任务了呢？比如，对于靠近边缘的光线，我们不再要求他继续保持出射角与入射角相等，而是弯折一些，这样不就可以记录更大的视角范围了吗？而且物体的长度也不至于被拉伸得很厉害。

人们想到了水下的鱼。由于水的折射率比空气大，光线从空气进入水中，折射角比入射角更小，并且入射角越大，这个变小的程度也越大。这正好是我们所需要的特性。由于这个特性，使得水下的鱼在向上看的时候，能一眼看到整个水面上的这个半球形空间；这整个空间的影像，都被「扭曲」、「压缩」到了一个半顶角约为 48° 的锥形内。

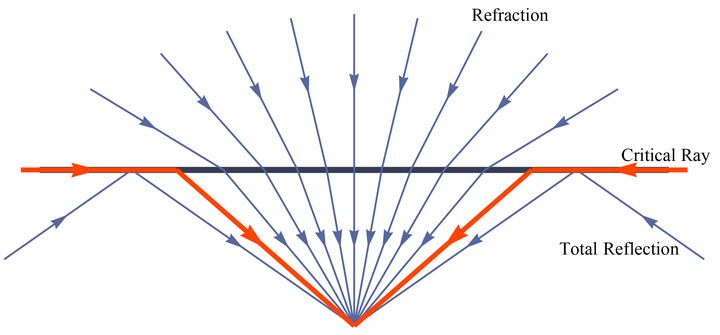
（空气-水界面处的光线折射与全反射）

在这个锥形空间内部，是来自水面上的空间的光线，在这个锥形外部，是来自水面下景色的反射。也就是说，在水下向上看，在一个圈之外，只能看到水底的景色；所有水面上的景色，都被压缩在一个圈内。这个圈，也叫「斯涅耳窗口（Snell's window）」（图片来自 Snell's window）。

（斯涅耳窗口现象）

上图就是典型的斯涅耳窗口现象，从水下向上看，只有一个圈内是亮的（来自水面上方的光线），在圈外是暗色的水底的反射。我们可以想象，如果水面平静没有涟漪，那么这个圈内是可以看到水面上空间的景物的。如果这样拍一张照片，就可以在一个合理的照片大小范围内，记录整个水面上的半球空间内的景象。有效的视角范围接近 180°，远远超过普通超广角镜头记录的范围。

正因为从水中向上看有这样奇妙的特性，人们受此启发，制造了鱼眼镜头。鱼眼镜头与这个场景类似，也是把很大角度范围内的光线进行「压缩」和「扭曲」，压进一个相对较小的空间内，从而可以被相机所记录下来。从这个角度可以说，鱼眼镜头是受到鱼眼看到的景象的启发而发明的，这也是鱼眼镜头这个名字的来历。当然，鱼眼镜头的前镜组大多具有一个极凸的镜片表面，看起来外形上也让人联想到鱼的眼睛，鱼眼镜头这个名字可以说也是非常贴切了。

3 鱼眼镜头的投影方式

我们已经知道，从数学上来说，普通的镜头成像相当于进行了一次射影变换。那么鱼眼镜头是一个什么变换呢？我们来看看，鱼眼镜头的变换，需要有什么样的特性。

首先当然是视角要大。或者说，对于某一个入射角，经过镜头之后射向成像面的出射角，一定是要小于入射角的。否则没办法在一个相对较小的范围内记录极大的视角。

第二，最好这个变换有比较良好的性质。这一点比较模糊，什么叫「良好的性质」？比如说普通镜头对应的射影变换，就有良好的性质，经过射影变换后，很多几何特征能保持不变，直线还是直线、圆锥曲线还是圆锥曲线。我们希望鱼眼镜头对应的这个变换，也能够保持一些几何特征不变。比如，变换前后，圆还是圆；比如，变换前后，一块空间所占的立体角不变。

第三，最好这个变换的形式比较简单。简单的形式方便让人从成像中直接观测、推断，而不用经过复杂的运算才能看出拍的是个什么东西。

我们来看看，满足这三个条件的情况下，鱼眼镜头可以有什么样的变换形式（我们把这种变换叫做投影，Projection）。为了直观地感受不同投影方式带来的差异，我写了一个简单的图形渲染器。受到 WiKi Fisheye lens 中的场景启发，我设置了一个差不多的场景，是一个直筒型的管道，管道壁上有规则的颜色格子。在这个场景中用不同的投影方式去模拟鱼眼镜头拍摄的图像，以便让大家有一个直观的感受。

（模拟场景管道内，普通 14mm 超广角不同视角拍摄的效果，没看明白这个场景的可以看文末彩蛋的动画演示）

斯涅耳窗投影，也就是真的去模仿水下鱼类向上看的时候的场景，我把这个投影方式叫做斯涅耳窗投影。用公式表达出射角和入射角之间的关系是 θ′=sin−1⁡(sin⁡θ/n)，其中 θ 是入射角，θ′ 是出射角，n 是水的折射率。很显然，这种投影方式最大的视角不会超过 180°。这种投影方式没什么特别的用处，在这里也只是作为最初的起点。现实中我从来没见哪个鱼眼镜头是用这种投影方式的。

（斯涅耳窗投影效果）

等积投影（Equisolid angle，equal area），也叫等立体角投影。用公式表达物体成像后与画面中心的距离 r 与入射角 θ 之间的关系就是 r=2fsin⁡(θ/2)。这种投影方式的特征在于，能保持变换前后，物体所占的立体角大小不变。或者说，在半球形空间中，半球面上两个「面积」相同的图案，成像后，在成像平面上的两个图案的面积仍然相同（虽然两者形状不一定相似）。这正是这个投影方式名字的由来。这种特性使得这个投影方式被广泛应用，其中一种场合就是测量全天云量覆盖情况。整个天空中云量覆盖多少，是由云所占的空间立体角的比例决定的。用这种投影方式的镜头，直接对着天空拍一张，在照片中测量一下云所占的像素面积比例，就得到了全天云量覆盖情况。在下图的模拟场景中，圆筒壁上每一列的各个小方格的面积都是相等的。

（等积投影效果）

等距投影（Equidistance，linear scaled）。这种投影方式的特点是，物体在成像面上离开画面中心的距离，与物体在空间中离开光轴的角度成正比，这个比例系数就是镜头焦距。用公式表达这个距离与角度的关系就是 r=fθ，其中 r 就是物体的像到画面中心的距离，就是入射角，也等于物体在空间中离开光轴的角度。在这种投影变换下，物体离开中心的距离（角度）就是一个重要的几何性质，物体的空间角距离与物体的像在像平面上的平面距离，是成正比的。这也是这个投影方式名称的来源。这种方式的镜头较少，然而更多地用在军事领域。想像一下武器瞄准系统，使用这种投影方式的镜头，不仅监测的视野范围大，而且对于目标的方位角度，只要直接在画面里测量平面距离就可以了，非常方便。在下图的模拟场景中，中间一列的各个小方格的高度都是一样的。

（等距投影效果）

体视投影（Stereographic，conform）。用公式表达就是 r=2ftan⁡(θ/2)，其中各个符号含义同前。这种投影方式的特点是能保持角度不变，这在数学上是一个非常良好的性质，叫做「保角变换（Conform）」，数学中有关保角变换的研究，可以整整写出好几本书，这里就不再展开更多了。保持角度不变，意思是任何直线相交的角度，在变换之后是保持不变的（虽然直线本身可能变弯曲）。在保角变换下，一个圆仍然还是一个圆（直线可以看做直径无穷大的圆），所以在某种程度上，保角变换也是保持了「形状」不变的。在下面的模拟场景中，圆筒壁上的所有边界线，全部都变成了圆弧；所有线的交角，也都保持了 90° 不变。