[摘抄]信号调制简述
带宽
带宽指信号所占据的频带宽度。由信号频谱图可以观察到一个信号所包含的频率成分。把一个信号所包含谐波的最高频率与最低频率之差，即该信号所拥有的频率范围，定义为该信号的带宽，又称为频宽，以赫兹（Hz）为单位。因此可以说，信号的频率变化范围越大，信号的带宽就越宽。
信号带宽远小于中心频率的是窄带信号，带宽能和中心频率相比拟或着是远大于中心频率的信号是宽带信号。窄带信号的功率集中在中心频率附近，两者的功率谱密度和频谱密度图有很大的差距。处理方法也有很大差距 一般认为宽带信号与窄带信号是相对的，不满足窄带条件的信号就称为宽带信号。若信号带宽为B ，时宽为T，中心频率为f_0，则窄带信号的定义有：
定义1： B << f_0，即相对带宽B/f_0<< 1 ,一般B/f_0< 0.1。
定义2： 2v/c<<1/TB,其中v是阵列与目标的相对径向运动速度，c 是信号在介质中的传播速度。
定义3：( N－1) d/c<<1/B，其中N 是阵元数目，d 是阵元间距。
定义4：2 Bτθ +1≈1 ,其中τθ是整个阵列以及延迟线的延时之和。
定义5：该信号空间协方差矩阵在没有噪声时的第二个特征值小于噪声功率。
“定义1”是对窄带信号的直观理解,同时也是窄带实信号可有效表示为其复解析形式的充分条件,在很多文献中均以该定义来区分信号是宽带信号还是窄带信号。
“定义2”是指在存在相对运动的系统中,在信号的持续时间T内,相对于信号的距离分辨率,目标没有明显的位移,此时信号可视为窄带信号,否则信号就是宽带信号。
“定义3”是指在阵列信号处理中,如果信号带宽的倒数远远大于信号掠过阵列孔径的最大传播时间,就称为窄带信号,否则为宽带信号。
“定义4”和“定义5”是从阵列采样数据自相关矩阵特征值的角度来定义窄带信号的,窄带情况下,阵列采样数据自相关矩阵的大特征值个数等于信号个数。
什么是时宽？
时宽一般更多指脉冲信号的持续时间，就是脉冲宽度，雷达发射信号是脉冲，一般认为是方波，那这个方波的迷之凸起的长度就是时宽。信号时宽越宽，即持续时间越长，其频带宽度越窄；时宽越窄，频宽越宽。至极限情况的话，时域上无限长的信号频域上有限，时域有限长则频域无限。
脉冲信号
是一种离散信号，形状多种多样，与普通模拟信号（如正弦波）相比，波形之间在Y轴不连续（波形与波形之间有明显的间隔）但具有一定的周期性是它的特点。最常见的脉冲波是矩形波（也就是方波）。脉冲信号之间的时间间隔称为周期；而将在单位时间（如1秒）内所产生的脉冲个数称为频率。
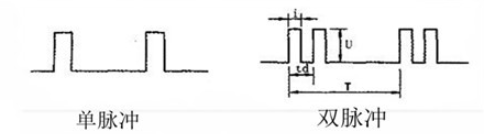
CW信号
CW：可以说有两种意义，一种是连续波信号，实际上就是正弦波做载波，CW可以包含线性调制（AM，DSB，SSB，VSB等）、非线性调制（FM、PM）、数字调制（ASK、FSK等）。
AM（调幅）、FM（调频）、PM（调相）
另一种cw就是等幅度连续波：
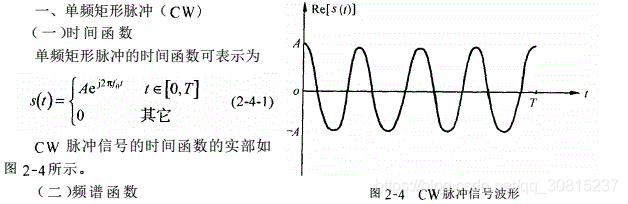
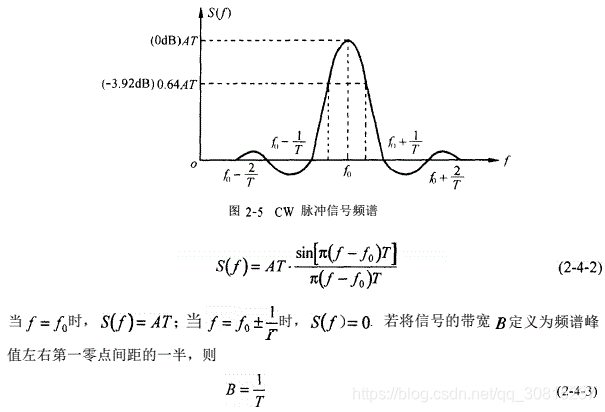
线性调频信号
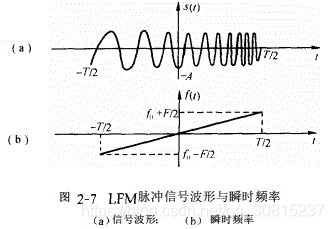
线性调频信号是一种脉冲压缩信号，具有作用距离远，分辨率高的特点，由于发送LFM信号时声音类似鸟叫，又被称为chirp信号（鸟鸣信号）。
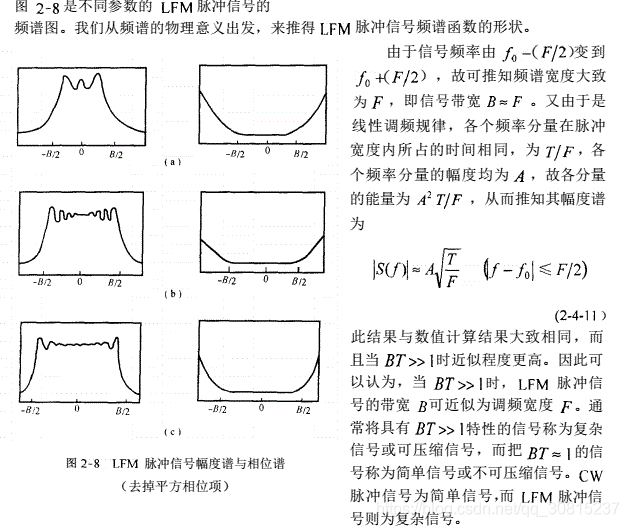
线性调频信号是一种大时宽带宽积信号。线性调频信号的相位谱具有平方律特性，在脉冲压缩过程中可以获得较大的压缩比，其最大优点是所用的匹配滤波器对回波信号的多普勒频移不敏感，即可以用一个匹配滤波器处理具有不同多普勒频移的回波信号，而且线性调频信号有着良好的距离分辨率和径向速度分辨率。因此线性调频信号是现代高性能雷达体制中经常采用的信号波形之一，因而可在工程中得到广泛的应用。
线性调频信号的复数表达式为：
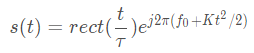
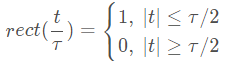
信号的瞬时频率f(t)：
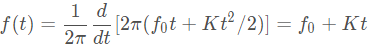
线性调频信号MATLAB代码：
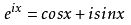
%线性调频信号的产生
clear all;
clc;
%%信号的参数设置
T=10e-6; %脉冲持续时间，10us
B=30e6; %线性调频带宽 30MHz
K=B/T; %斜率
Fs=2*B;Ts=1/Fs; %采样频率，采样周期
N=T/Ts; %采样点数
f0 = 5e6; %发射信号时的瞬时频率，也就是中心频率
t=linspace(-T/2,T/2,N);
A0 = 1; %发射信号的振幅
Phi0 = 0; %发射信号的随机初相
%%产生线性调频信号
St1=exp(1j*pi*K*t.^2); %generate chirp signal
%St1=exp(j*(2*pi*f0*t-pi*K*t.^2)) %线性调频信号复数表达式
St2=cos(pi*K*t.^2);
%St2=cos(2*pi*f0*t+pi*K*t.^2) %线性调频信号的余弦表达式,即St1的实部
figure,subplot(311)
plot(t*1e6,real(St1));
xlabel('Time（us）');
ylabel('Amplitude(Watts)')
title('线性调频信号的实部');
grid on;axis tight;
subplot(312),plot(t*1e6,imag(St1));
xlabel('Time（us）');ylabel('Amplitude(Watts)')
title('线性调频信号的虚部');
grid on;axis tight;
subplot(313)
freq=linspace(-Fs/2,Fs/2,N);
plot(freq*1e-6,fftshift(abs(fft(St1)))); %先对St1做傅里叶变换得到频谱，在取幅度值，然后将其移动到频谱中心
xlabel('Frequency（MHz）');ylabel('Amplitude(Watts)')
title('线性调频信号的频谱');
grid on;axis tight;
figure,subplot(211)
plot(t*1e6,real(St2));
xlabel('Time（us）');
ylabel('Amplitude(Watts)')
title('线性调频信号的实部');
grid on;axis tight;
subplot(212)
freq=linspace(-Fs/2,Fs/2,N);
plot(freq*1e-6,fftshift(abs(fft(St2))));
xlabel('Frequency（MHz）');
ylabel('Amplitude(Watts)')
title('线性调频信号的频谱');
grid on;
axis tight;
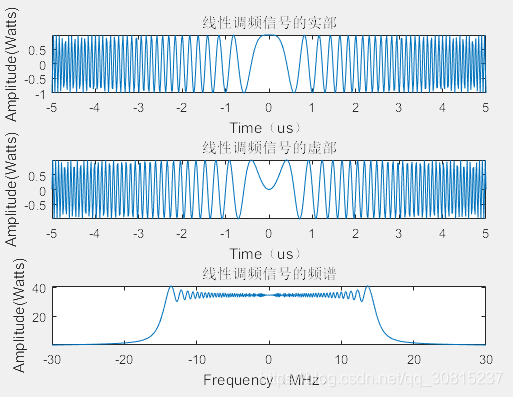
还有一点不得不强调，LFM脉冲信号的带宽和时宽都是可以自己选择的，不像矩形脉冲信号那样带宽和时宽相互制约。
————————————————
版权声明：本文为CSDN博主「菜鸟知识搬运工」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/qq_30815237/article/details/106722823
