[摘抄]LTspice基础教程-025.电路容差分析，蒙特卡罗分析(Monte Carlo)

容差分析技术是一种预测电路性能参数稳定性的方法。它主要研究电路组成部分参数偏差，在规定的使用条件范围内，对电路性能容差的影响。
　　电路容差分析包括如下几种方法：

最坏情况实验法
最坏情况分析法（包括线性展开法、直接代入法）
蒙特卡罗法
伴随网络法
矩阵法
  LTspice中有三个函数和容差分析有关，分别是：

mc(x,y)
官方解释：A random number between x*(1+y) and x*(1-y) with uniform distribution.
mc应该是Monte Carlo的缩写。
该函数返回x * ( 1 + y ) 和 x * ( 1 - y ) 之间具有均匀分布的随机数。

flat(x)
官方解释：Random number between -x and x with uniform distribution.
该函数返回 - x 和 x 之间具有均匀分布的随机数。
m c ( x , y ) 作 用 等 同 于 x ∗ ( 1 + f l a t ( y ) ) 。 \color{red}{ mc(x,y)作用等同于{ x * ( 1 + flat( y ) ) }。 }mc(x,y)作用等同于x∗(1+flat(y))。

gauss(x)
官方解释：Random number from Gaussian distribution with sigma of x.
该函数返回标准差σ为 x 的高斯随机数。

 

  使用LTspice进行蒙特卡罗分析大概流程如下：

修改元器件标称值为随机数；
进行指定次数仿真
  如下图搭建一简单电路演示具体如何操作：

 

 

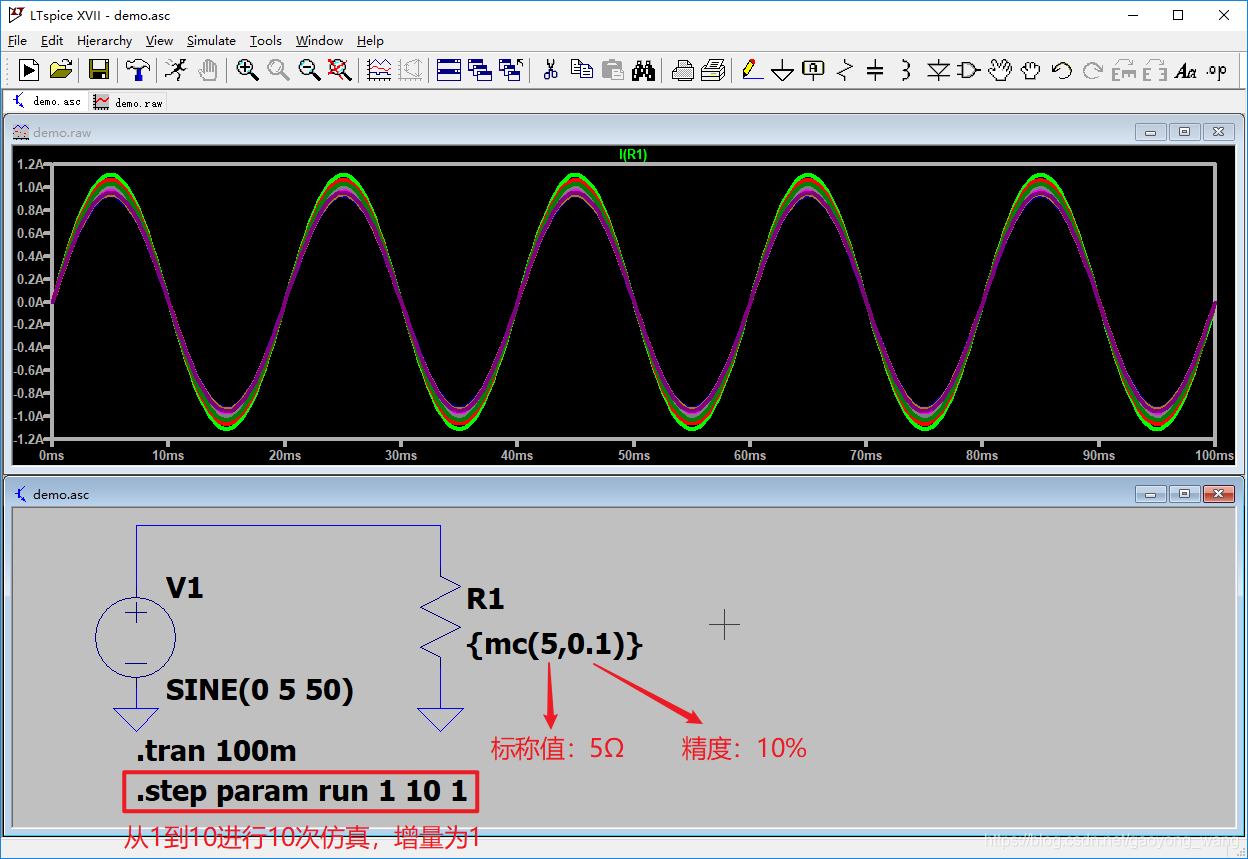
  上图中的step指令参数名“run”可以随便取名，实验发现LTspice的step指令中参数名只要原理图中未声明，LTspice就会理解成计算次数。
　　在原理图中添加meas指令，测量电流的最大值：
　　.meas MaxOfCurrent MAX I(R1)　　

 

 

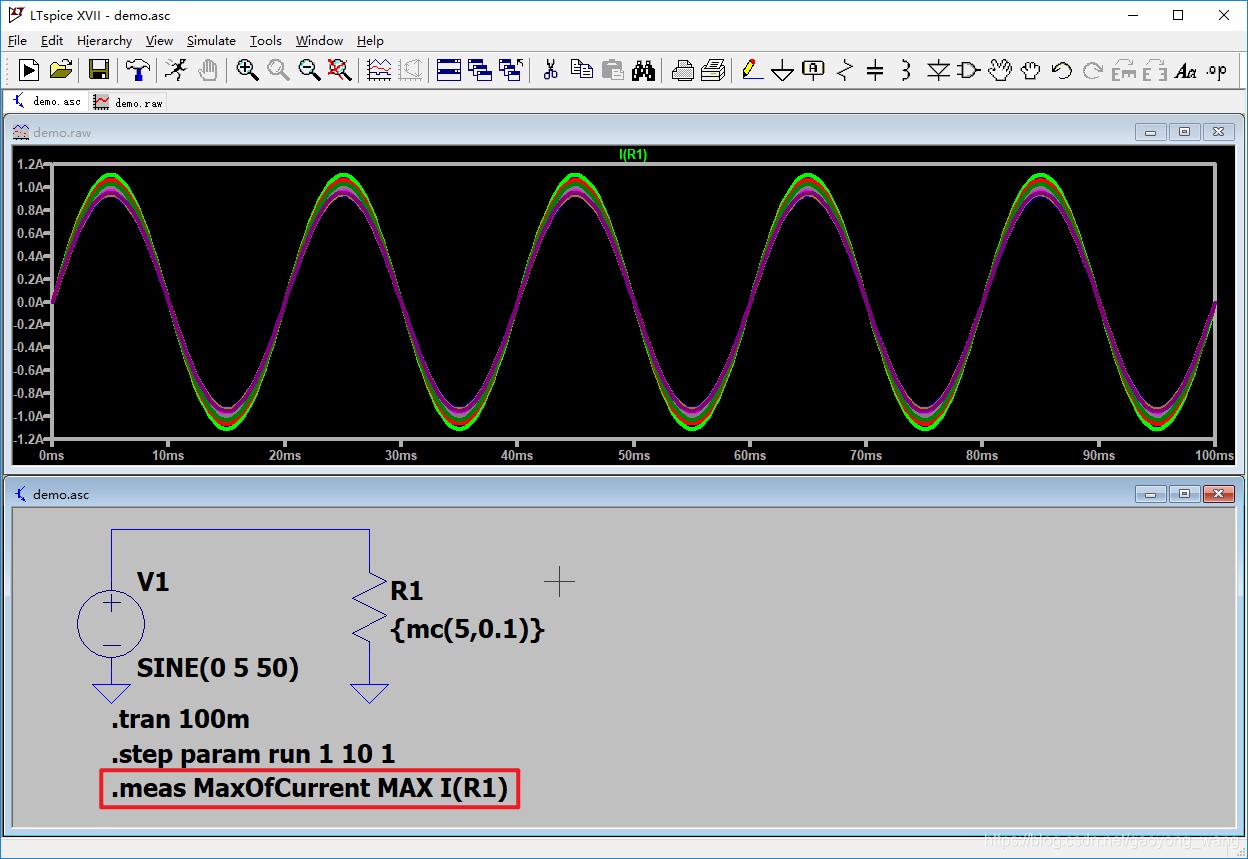
　　运行完仿真，可以将10次仿真的最大值进行绘图，具体操作如下：

 

 

　　当然这个绘图没啥实际意义，这里只是提一下有这么个功能。
　　

  另有资料表明，使随机数生成器种子取决于PC的实时时钟，产生的随机数更加真实。设置如下：

 

 

 

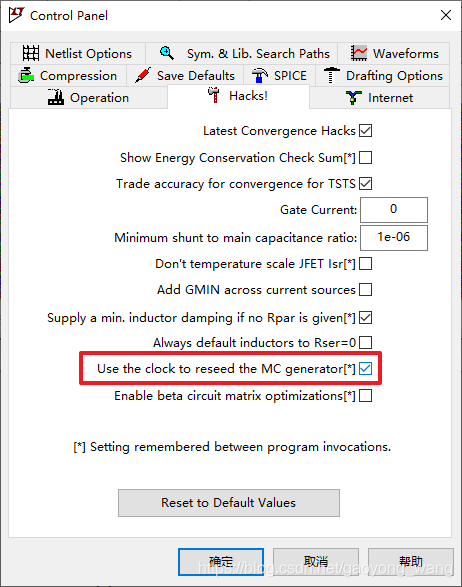
  特殊说明：注意MC函数是均匀分布的。
————————————————
版权声明：本文为CSDN博主「gaoyong_wang」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/gaoyong_wang/article/details/105185576