字符串匹配算法 BF & KMP 算法
1. 定义
-
主串(
S): 匹配的目标串,这里用S来表示 -
模式串(
T): 需要匹配的字符串,这里用T来表示 -
BF算法: BF算法,即暴风(Brute Force)算法,是普通的模式匹配算法,BF算法的思想就是将目标串S的第一个字符与模式串T的第一个字符进行匹配,若相等,则继续比较S的第二个字符和 T的第二个字符;若不相等,则比较S的第二个字符和T的第一个字符,依次比较下去,直到得出最后的匹配结果。BF算法是一种蛮力算法。 BF算法的时间复杂度O(MN)*。
-
KMP算法: KMP算法是一种改进的字符串匹配算法,由D.E.Knuth,J.H.Morris和V.R.Pratt提出的,因此人们称它为克努特—莫里斯—普拉特操作(简称KMP算法)。KMP算法的核心是利用匹配失败后的信息,尽量减少模式串与主串的匹配次数以达到快速匹配的目的。具体实现就是通过一个
next()函数实现,函数本身包含了模式串的局部匹配信息。KMP算法的时间复杂度O(m+n)。 -
字符串匹配算法:用来查找
S串在T串中是否存在及所处位置,本文将使用BF算法和KMP算法进行讲解字符串匹配算法。
2. BF算法
本算法使用暴力破解的方式进行匹配,当模式串T从目标串S的i位开始匹配,到i+n位失配时,目标串S回溯到i+1位,模式串T回溯到0位
如下图,主串从第2位匹配到第8位时失配
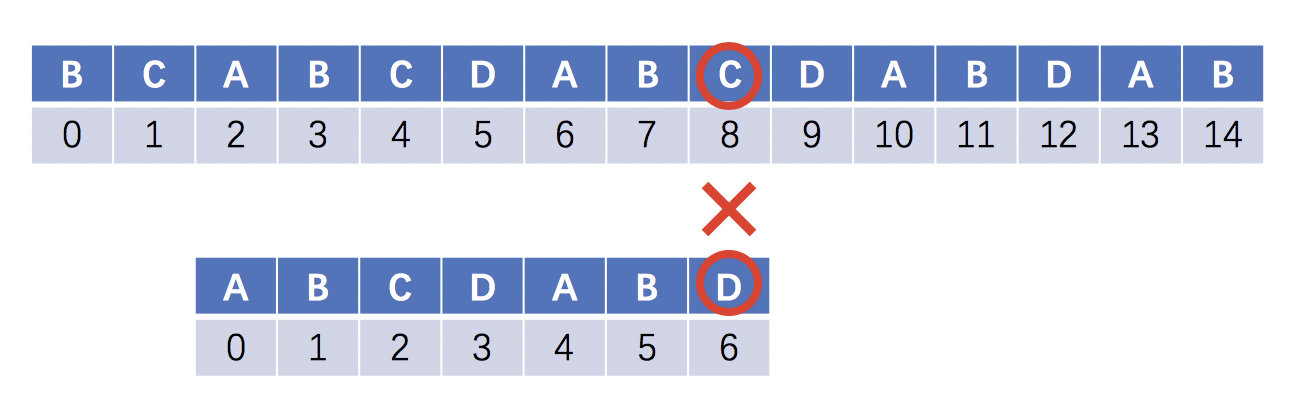
匹配位置i回溯,主串回溯到(2+1)位,模式串回溯到0位重新开始匹配
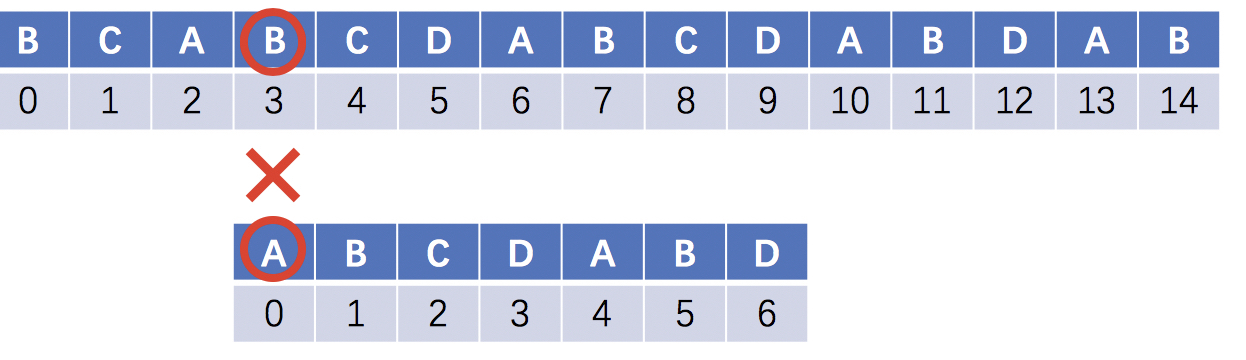
缺点:相比于KMP算法,BF算法包含了很多不必要的回溯
算法实现
public class BFExample {
public static void main(String[] args) {
String S = "ABCBABCDEF";
String T = "ABCD";
int pos = 0;
BFExample test = new BFExample();
// 递归匹配
System.out.println(">>>>>>>>>>>>> 递归匹配T串在S串中的位置");
int begin1 = test.indexOfBFRecursion(S, T, pos);
if (begin1 >= 0) {
// 匹配到了
int end1 = begin1 + T.length() - 1;
System.out.println(String.format("%s 位于 %s 的%d-%d位", T, S, begin1, end1));
} else {
// 没匹配到
System.out.println(String.format("%s 不在 %s 中", T, S));
}
// 非递归匹配
System.out.println(">>>>>>>>>>>>> 非递归匹配T串在S串中的位置");
int begin2 = test.indexOfBF(S, T, pos);
if (begin2 >= 0) {
// 匹配到了
int end2 = begin2 + T.length() - 1;
System.out.println(String.format("%s 位于 %s 的%d-%d位", T, S, begin2, end2));
} else {
// 没匹配到
System.out.println(String.format("%s 不在 %s 中", T, S));
}
}
/**
* 使用递归方法,查询字符串T在S中的起始位置,从pos位置开始
* @param S 主串
* @param T 模式串
* @param pos 起始匹配位置
* @return
*/
public int indexOfBFRecursion(String S, String T, int pos) {
// 当起始匹配位置+模式串长度大于主串长度,说明模式串在主串中不存在
if (pos + T.length() > S.length()) {
return -1;
}
for (int i = 0; i < T.length(); i++) {
if (S.charAt(pos + i) != T.charAt(i)) {
// 出现不匹配的结果,递归且起始匹配位置pos+1
return indexOfBFRecursion(S, T, ++pos);
}
}
// 匹配到了,返回pos
return pos;
}
/**
* 使用非递归方法,查询字符串T在S中的起始位置,从pos位置开始
* @param S 主串
* @param T 模式串
* @param pos 起始匹配位置
* @return
*/
public int indexOfBF(String S, String T, int pos) {
// 当起始匹配位置+模式串长度大于主串长度,说明模式串在主串中不存在
if (pos + T.length() > S.length()) {
return -1;
}
// 遍历S串
for (int i = pos; i < S.length(); i++) {
int j;
// 循环匹配T串
for (j = 0; j < T.length(); j++) {
if (S.charAt(i + j) != T.charAt(j)) {
break;
}
}
// j == T.length(), 所有字符匹配成功,返回S的索引i
if (j == T.length()) {
return i;
}
}
// 没匹配到
return -1;
}
}
3. KMP算法
KMP算法的基本思路是先将模式串自我匹配,得到一个记录了回溯索引的数组next
这个数组产生的规则如下
- 前缀指的是从0位开始往后的子串
- 后缀指的是从当前位往前的子串
- 使用前缀和后缀相等的最大长度作为当前位的回溯索引
- 如ABCABX,当前位为X,前缀为AB,后缀为AB时相等且长度最长,那么X的回溯索引为2
3.1. next数组的生成算法
假设现在模式串T前缀匹配到 i 位置,后缀匹配到 j 位置
- 如果i = -1,或者当前字符匹配成功(即T[i] == T[j]),都令i++,j++,next[j] = i;后缀索引j的后一位对应的回溯索引是前缀索引+1(因为i和j都自增了,所以这里直接使用next[j] = i)
- 如果i != -1,且当前字符匹配失败(即T[i] != T[j]),则令 j 不变,i = next[i]。此举意味着失配时,前缀索引i移动到模式串的next[i]位
算法实现如下:
/**
* 生成next数组
* @param T
* @return
*/
public int[] getNext(String T) {
int len = T.length();
int[] next = new int[len];
int i = -1; // 前缀
int j = 0; // 后缀
next[0] = -1; // next[0]既数组第0个元素设置初始值-1,用作回溯判断
// 遍历T串
while (j < len - 1) {
/**
* -1 == i : 前缀没匹配到,从0开始重新匹配
* T.charAt(i) == T.charAt(j) : 匹配到了
* i和j都往后移一位
*/
if ( (-1 == i) || (T.charAt(i) == T.charAt(j)) ) {
i++;
j++;
next[j] = i;
} else {
// 根据已匹配到的next数组回溯i
i = next[i];
}
}
return next;
}
根据以上的规则能生成next数组
3.2. KMP算法匹配
上面生成next算法的规则和KMP匹配基本类似,
可以理解为回溯的next数组中记录的回溯的长度就是目标串S与模式串T匹配中T向右移可以复用的子串长度
如图,目标串S在索引8失配,模式串T在索引6失配,此时AB子串可以复用,所以可以将模式串T回溯到2位,再与目标串S的当前位匹配
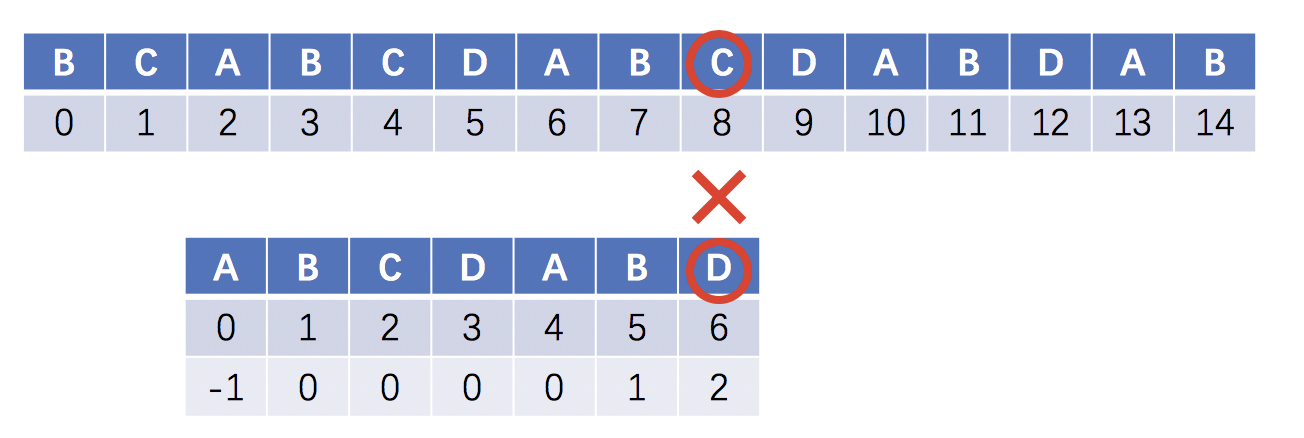
模式串T向右移动6-2位
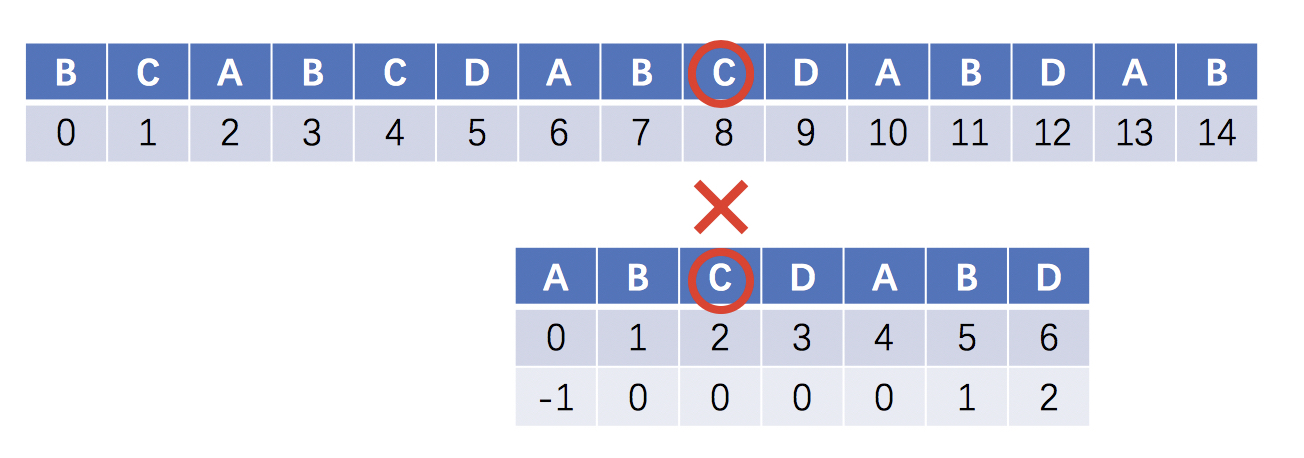
算法实现
public int indexOfKMP(String S, String T, int pos) {
int[] next = getNext(T);
int i = pos;
int j = 0;
while (i < S.length() && j < T.length()) {
/**
* -1 == j : j没匹配到,从0开始重新匹配
* S.charAt(i) == T.charAt(j) : 匹配到了
* i和j都往后移一位
*/
if ( (-1 == j) || S.charAt(i) == T.charAt(j)) {
i++;
j++;
} else {
// 根据next数组回溯j的位置
j = next[j];
}
}
// 模式串T匹配完成
if (j == T.length()) {
return i - T.length();
}
return -1;
}
3.3. next算法优化
next算法中计算了最长的前缀和后缀,但是在一下场景中存在优化点
当模式串T的第3位A失配时,按照前面的逻辑是回溯到第2位的A,但是由于A在目标串S的第3位失配,所以这里的回溯是多余的操作
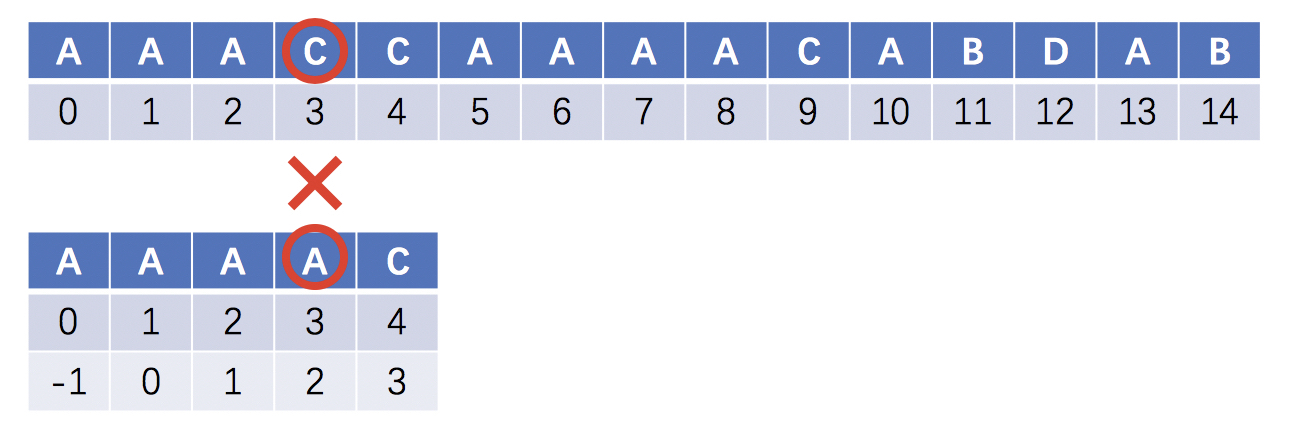
优化后的next在匹配到i和j位的字符相同时,直接在j位复用i位的索引,得到如下的next结构
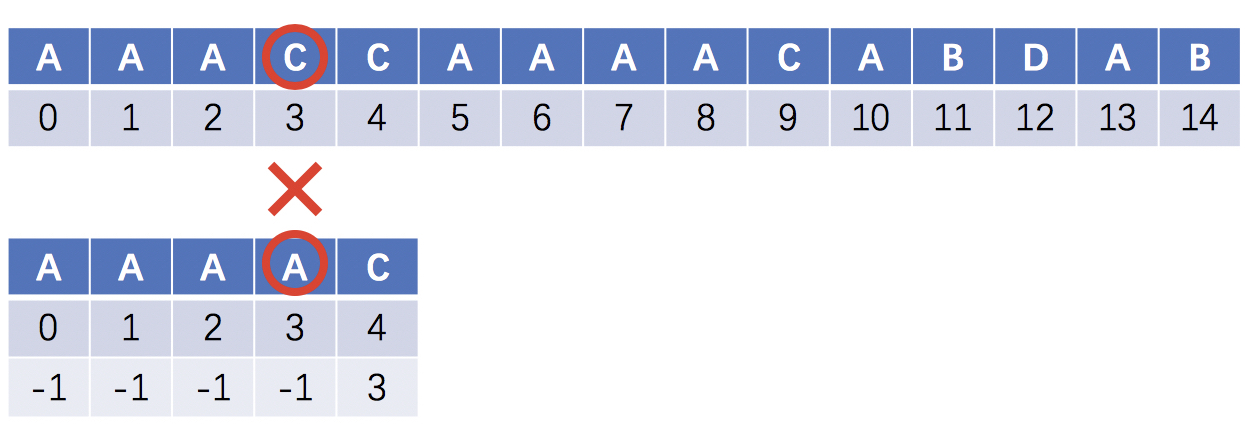
代码实现:
/**
* 生成next数组
* @param T
* @return
*/
public int[] getNext(String T) {
int len = T.length();
int[] next = new int[len];
int i = -1; // 前缀
int j = 0; // 后缀
next[0] = -1; // next[0]既数组第0个元素设置初始值-1,用作回溯判断
// 遍历T串
while (j < len - 1) {
/**
* -1 == i : 前缀没匹配到,从0开始重新匹配
* T.charAt(i) == T.charAt(j) : 匹配到了
* i和j都往后移一位
*/
if ( (-1 == i) || (T.charAt(i) == T.charAt(j)) ) {
i++;
j++;
/**
* 当前缀相等时,如果失配可以直接回溯到第一个之前的位置
* 如:T = XAAAAAX
* 当在T[5]处失配时,则证明T[1-4]也会失配,所以直接回溯到T[1]的值所指向的索引0
*/
// next[j] = i;
/******** 改进 ********/
if (T.charAt(i) != T.charAt(j)) {
next[j] = i;
} else {
next[j] = next[i];
}
/******** 改进 ********/
} else {
// 根据已匹配到的next数组回溯i
i = next[i];
}
}
return next;
}
END
以上算法就是KMP算法的大致讲解


 浙公网安备 33010602011771号
浙公网安备 33010602011771号