牛客编程巅峰赛S2第4场
牛客编程巅峰赛S2第4场
牛牛摆玩偶
题目描述
牛牛有\(n(2 \leq n \leq 10^5)(2≤n≤105)\)个玩偶,牛牛打算把这n个玩偶摆在桌子上,桌子的形状的长条形的,可以看做一维数轴。 桌子上有 \(M\) 个互不相交的区间\((1≤M≤10^5)\),这些区间上面可以放玩偶。一个位置只能放一个玩偶,玩偶之间的距离越大越美观,牛牛想最大化 D 的值,其中 D 为最近的两个玩偶之间的距离。请帮牛牛求出 D 的最大可能值。
示例1
输入
5,3,[[0,2],[4,7],[9,9]]
返回值
2
备注:
区间长度\(\leq 2^{31} -1\)
思路:
最大最小值,最小最大值,一看就是二分。比赛中就是过不了(\(90\%\)的数据), 肯定思路没错,以为是数据错了(*^▽^*)。
思路数据没错,应该首先想到是不是时间复杂度太高,应该是judge函数的时间复杂度高了。下次一定注意。
代码
/**
* struct Interval {
* int start;
* int end;
* Interval(int s, int e) : start(start), end(e) {}
* };
*/
#define ll long long
const int maxn = 2e5+10;
class Solution {
public:
/**
* 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可
*
* @param n int整型 玩偶数
* @param m int整型 区间数
* @param intervals Interval类vector 表示区间
* @return int整型
*/
bool judge(ll x, vector<pair<ll, ll> > inv, int n){
//n--;
ll pos = -2e10;
/* 复杂度太高?
for(auto ine : inv){
if(pos + x <= ine.first){
pos = ine.first;
n--;
}
if(n <= 0) return true;
while(pos + x <= ine.second){
pos += x;
n--;
if(n <= 0) return true;
}
}
*/
for(auto in : inv){
ll l = max(pos+x, in.first);
if(l > in.second) continue;
ll t = (in.second - l) / x;
n -= (t+1);
if(n <= 0) return true;
pos = l + t*x;
}
return n <= 0;
}
int doll(int n, int m, vector<Interval>& intervals) {
// write code here
vector<pair<ll, ll> > inv;
for(auto ine : intervals) {
inv.push_back({1ll * ine.start, 1ll * ine.end});
}
sort(inv.begin(), inv.end(), [](const pair<ll, ll> &a, const pair<ll, ll> &b)->bool{
return a.first < b.first;
});
ll l = 0, r = inv.back().second - inv[0].first;
ll ans = -1;
while(l <= r){
ll mid = l + (r - l) / 2;
if(judge(mid, inv, n)){
ans = mid;
l = mid + 1;
}else r = mid - 1;
}
return ans;
}
};
交叉乘
题目描述
上小学二年级的牛牛已经精通整数的加法和乘法。现在你要考考他。你先给出一个整数数组\(a_1,a_2,...,a_n\),然后每次你会给一对整数\(l,r(l≤r)\),牛牛需要算出\(\sum_{i=l}^{r} \sum_{j=i+1}^{r} a_i*a_j\)的值。但是牛牛算完之后你不能不确定他算得对不对,为了验证他的答案,你决定自己算一遍。
为了不输出过大的答案,假设答案为\(ans\),请输出\(ans \% 1,000,000,007\)。
提示:
在\(\%1,000,000,007\)的意义下\(/2\)相当于\(*500,000,004\)
示例1
输入
[1,2,5,3,4],[1,4,2,5,2,2]
返回值
[41,71,0]
说明
第一个询问,l=1,r=4,ans=1*2+1*5+1*3+2*5+2*3+5*3=41;
第二个询问,l=2,r=5,ans=2*5+2*3+2*4+5*3+5*4+3*4=71;
第三个询问,l=2,r=2,ans=0。
备注:
参数\(a\)为\(vector<int>\),依次为\(a_1,a_2,...,a_n\);
参数\(query\)为\(vector<int>\),依次为\(l_1,r_1,l_2,r_2,...,l_q,r_q\);
\(n\)为数组\(a\)长度,\(q\)为询问次数。
\(30\%\) 数据满足 \(1<=n,q<=1000\)
\(100\%\) 数据满足 \(1<=n,q<=100000,1<=a_i<=100000,1<=l_i<=r_i<=n\)
思路
没想出来,思路是听直播学的。
九九乘法表,划掉对角线,前缀和优化。
就是主对角线下面的等式之和,矩阵里对角线上面的元素和下面的元素和相同,故可以总体相加,如下图:
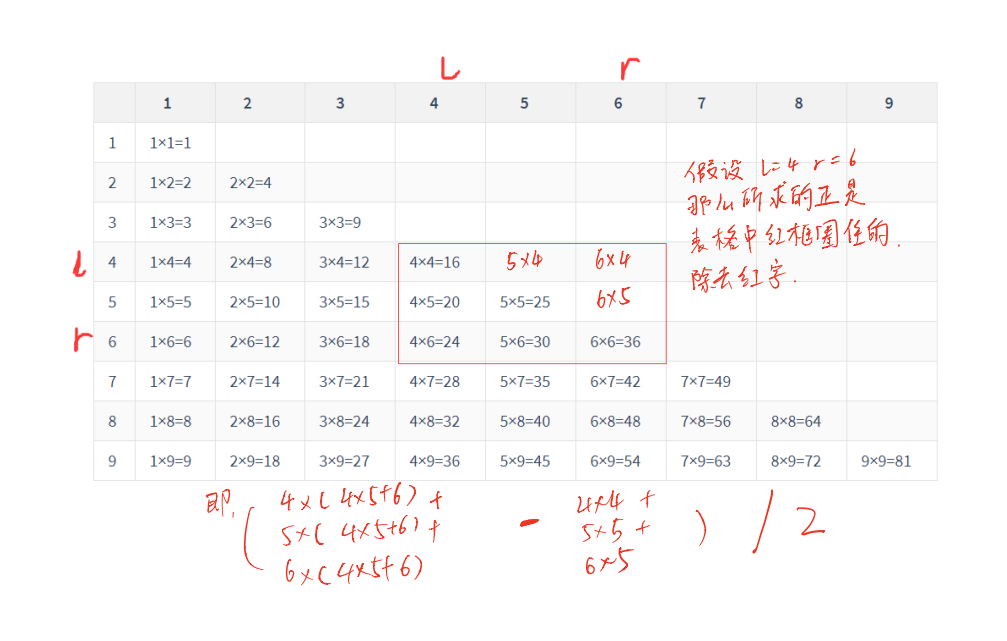
求和公式:\(\sum_{i=l}^{r} \sum_{j=i+1}^{r} a_{i} * a_{j}=\frac{\left(\sum_{i=l}^{r} a_{i}\right)^{2}-\sum_{i=l}^{r} a_{i}^{2}}{2}\)
另外:题目中数较大。需要开long long。用到了逆元的知识。
代码
#define ll long long
const int mod = 1e9+7;
const int maxn = 2e5+10;
ll sum[maxn], mul[maxn];
class Solution {
public:
/**
* 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可
* 多次求交叉乘
* @param a int整型vector a1,a2,...,an
* @param query int整型vector l1,r1,l2,r2,...,lq,rq
* @return int整型vector
*/
vector<int> getSum(vector<int>& a, vector<int>& query) {
// write code here
sum[0] = mul[0] = 0;
for(int i = 1; i <= a.size(); i++){
sum[i] = (sum[i-1] + a[i-1]) % mod;
mul[i] = (mul[i-1] + 1ll * a[i-1]*a[i-1] % mod) % mod;
}
vector<int> ans;
for(int i = 0; i < query.size(); i+=2){
int l = query[i], r = query[i+1];
ll t = (sum[r] - sum[l-1]) % mod;
ll res = (t * t % mod - (mul[r]-mul[l-1])% mod + mod)% mod ;
res = (res * 500000004 % mod + mod) % mod;
ans.push_back(res);
}
return ans;
}
};


