codeforces 1325 F. Ehab's Last Theorem
codeforces 1325 F. Ehab's Last Theorem
题意:
给一个\(n\)个点的无向图(无重边、自环),要找出包含不少于\(⌈n⌉\)个点的简单环或独立集。
题解:
性质:如果无向图中不存在不少于\(⌈n⌉\)个点的简单环,则必然存在不少于\(⌈n⌉\)个点的独立集。
证明:令\(sq=\lceil \sqrt{n} \ \rceil\), 先找一个dfs树\(\ ^①\) ,标记节点深度,如果一条非树边(back-edges)连接的两个点的深度的差大于等于\(sq-1\),那么就找到一个至少包含\(⌈n⌉\)个顶点的环了,输出。
如果所有的非树边都不满足上述条件的话,那么每个节点最多只会有\(sq-2\)个非树边,因为如果有\(sq-1\)个非树边的话,那么两点之间深度差至少为\(sq-1\),于是一定可以找到一个含有\(sq\)个节点的点最大独立集。
因为每个点最多有\(sq - 2\)条非树边,说明选择一个点最多导致\(sq - 2\)个点不能被选择,所以可以选出大小至少为\(sq\)的独立集。
AC代码:
#include<bits/stdc++.h>
using namespace std;
#define pb push_back
const int maxn = 2e5 + 10;
int n, m, sq;
vector<int> G[maxn];
vector<int> ans1, ans2;
int dep[maxn], vis[maxn];
void dfs(int u){
ans2.pb(u);
dep[u] = ans2.size();
for (int i = 0; i < G[u].size(); i++){
int v = G[u][i];
if(!dep[v])
dfs(v);
else if(dep[u] - dep[v] >= sq-1){
cout << 2 << endl;
cout << dep[u] - dep[v] + 1 << endl;
for (int i = dep[v] - 1; i < dep[u]; i++){
cout << ans2[i] << " ";
}
cout << endl;
exit(0);
}
}
if(!vis[u]){
ans1.pb(u);
for (int i = 0; i < G[u].size(); i++){
int v = G[u][i];
vis[v] = 1;
}
}
ans2.pop_back();
}
int main(){
ios_base::sync_with_stdio(0);
memset(vis, 0, sizeof(vis));
memset(dep, 0, sizeof(vis));
cin >> n >> m;
sq = sqrt(n - 1) + 1;
for (int i = 0; i < m; i++){
int x, y;
cin >> x >> y;
G[x].pb(y); G[y].pb(x);
}
dfs(1);
cout << 1 << endl;
for (int i = 0; i < sq; i++){
cout << ans1[i] << " ";
}
cout << endl;
return 0;
}
① dfs树:
[不想看英文解释可以往下拉。]
The DFS tree
Consider an undirected connected graph \(G\). Let's run a depth-first traversal of the graph. It can be implemented by a recursive function, perhaps something like this:
1 function visit(u):
2 mark u as visited
3 for each vertex v among the neighbours of u:
4 if v is not visited:
5 mark the edge uv
6 call visit(v)
Here is an animation of what calling visit(1) looks like.
Let's look at the edges that were marked in line 5. They form a spanning tree of \(G\), rooted at the vertex 1. We'll call these edges span-edges; all other edges are called back-edges.
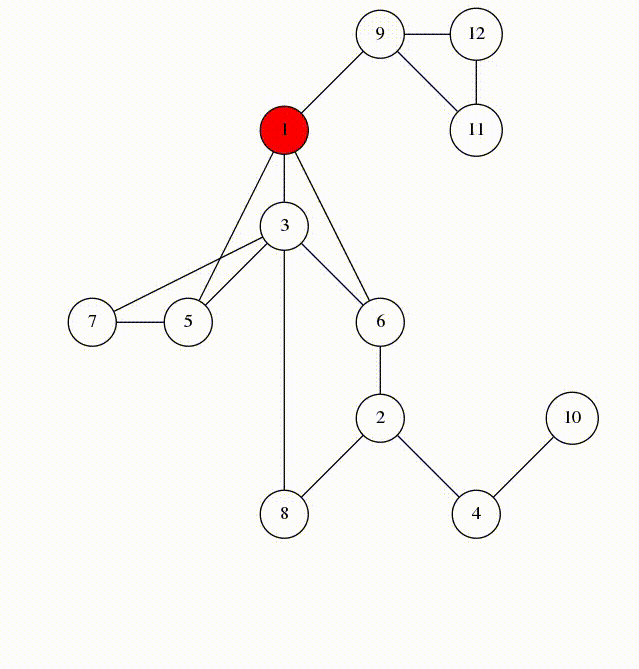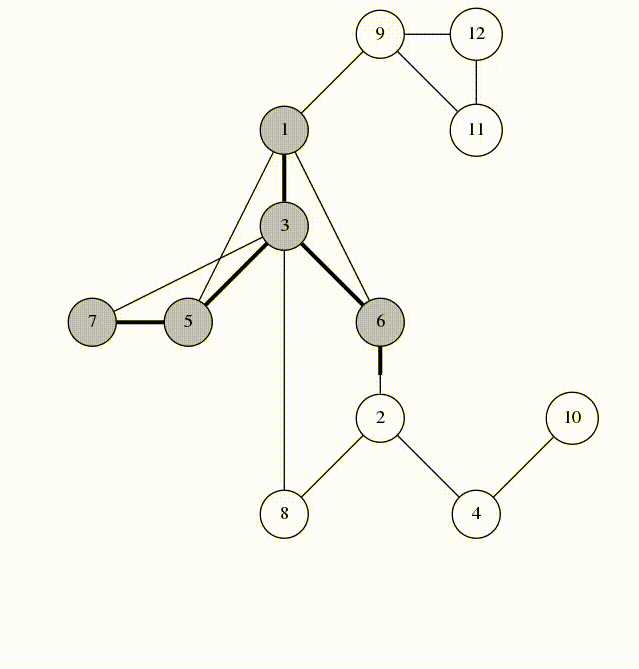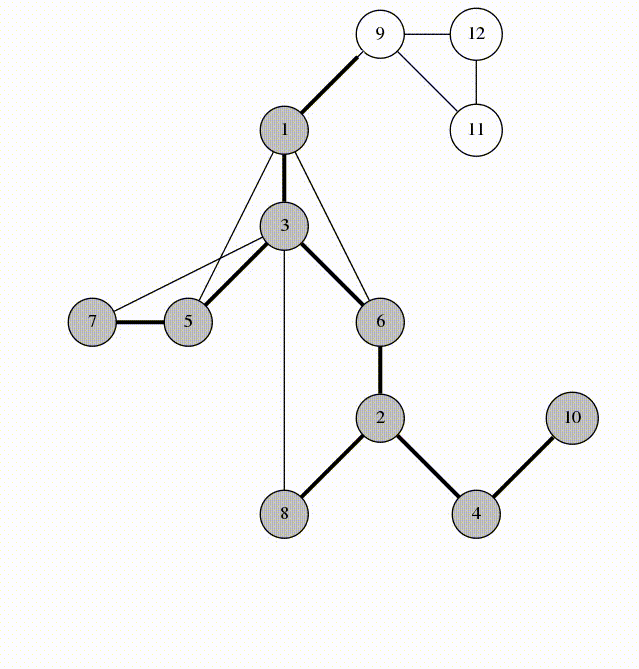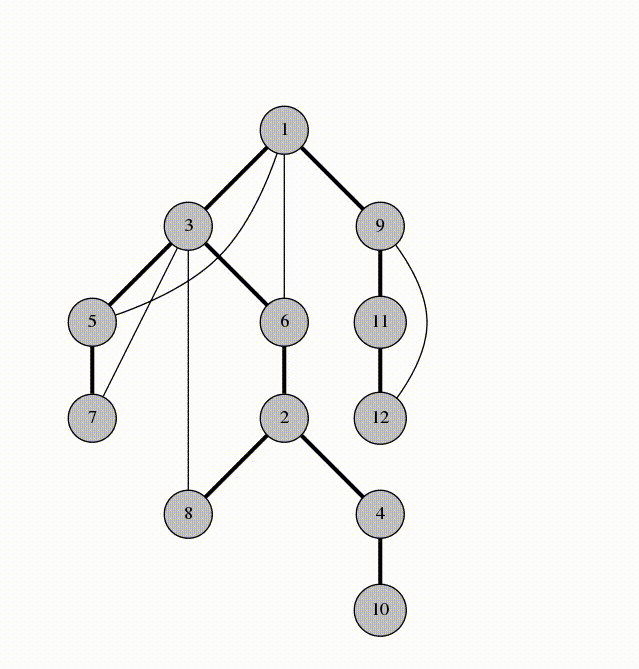
This is the DFS tree of our graph:
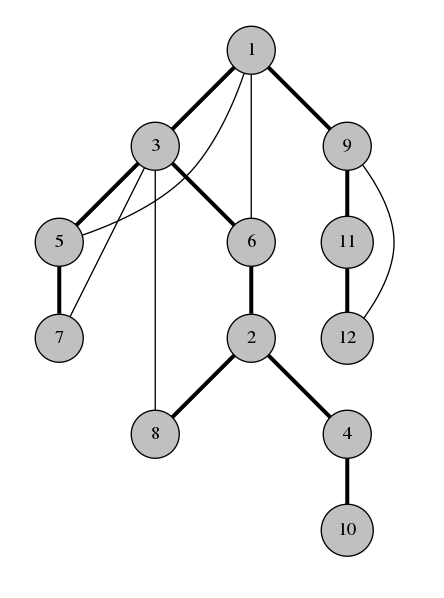
Observation 1. The back-edges of the graph all connect a vertex with its descendant in the spanning tree. This is why DFS tree is so useful.
Why?
Suppose that there is an edge \(uv\), and without loss of generality the depth-first traversal reaches \(u\) while \(v\) is still unexplored. Then:
if the depth-first traversal goes to \(v\) from \(u\) using \(uv\), then \(uv\) is a span-edge;
if the depth-first traversal doesn't go to \(v\) from \(u\) using \(uv\), then \(v\) was already visited when the traversal looked at it at step 4. Thus it was explored while exploring one of the other neighbours of \(u\), which means that \(v\) is a descendant of \(u\) in the DFS tree.
For example in the graph above, vertices 4 and 8 couldn't possibly have a back-edge connecting them because neither of them is an ancestor of the other. If there was an edge between 4 and 8, the traversal would have gone to 8 from 4 instead of going back to 2.
This is the most important observation about about the DFS tree. The DFS tree is so useful because it simplifies the structure of a graph. Instead of having to worry about all kinds of edges, we only need to care about a tree and some additional ancestor-descendant edges. This structure is so much easier to think and write algorithms about.
性质:
一条非树边连接了一个点和它在生成树中的一个后代
证明:假设我们有一条边\((u,v)\),并且现在我们dfs到了u。
1.如果v没有被访问,那么(u,v)就是一条树边
2.如果v已经被访问了,就说明要么v是u的祖先,要么v在u的一个儿子的一个子树中(因为v已经被访问了),也就是说v是u的后代。
证毕。
附:
- 原dfs树链接:dfs树,列举了dfs树的各个应用,讲得很详细。

