【题解】杂题选讲
杂题选讲
AT_abc350_g [ABC350G] Mediator
先考虑没有加边操作，如何回答询问？
设 \(fa_x\) 表示 \(x\) 的父亲，那么对 \((x,y)\) 的询问有解只有三种情况。
\(fa_x=fa_y\ne 0, fa_{fa_x}=y, fa_{fa_y}=x\)。
只需要维护 \(fa\) 数组即可回答所有询问，如何维护？使用启发式合并，当两个快合并的时候，暴力修改小块的 \(fa\) ，这样没个点每次被暴力修改，所在联通块大小至少翻倍，最多被暴力修改 \(\log n\) 次。
连通性可以使用并查集维护。时间复杂度 \(\mathcal{O}(n\log n)\)。
#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N = 1e5+5,mod = 998244353;
int n,q,f[N],sz[N],ff[N];
vector<int> g[N];
void dfs(int u,int fa){
f[u] = fa;
for(auto v:g[u]){
if(v==fa) continue;
dfs(v,u);
}
}
int find(int x){
if(x==ff[x]) return x;
return ff[x] = find(ff[x]);
}
inline void merge(int x,int y){
int fx = find(x),fy = find(y);
if(sz[fx]>sz[fy])
swap(x, y), swap(fx, fy);
dfs(x, y);
sz[fy] += sz[fx], ff[fx] = fy;
g[x].push_back(y), g[y].push_back(x);
}
signed main(){
cin >> n >> q;
for (int i = 1; i <= n; i++)
sz[i] = 1, ff[i] = i;
int las = 0;
while (q--){
int op, u, v;
cin >> op >> u >> v;
op = (op * (1 + las)) % mod % 2 + 1, u = (u * (1 + las)) % mod % n + 1, v = (v * (1 + las)) % mod % n + 1;
if (op == 1)
merge(u, v);
else{
las = 0;
if (f[u] == f[v] && f[u] != 0)
las = f[u];
else if (f[f[u]] == v)
las = f[u];
else if (f[f[v]] == u)
las = f[v];
cout << las << endl;
}
}
return 0;
}
CF1898D Absolute Beauty
首先考虑转换成区间。
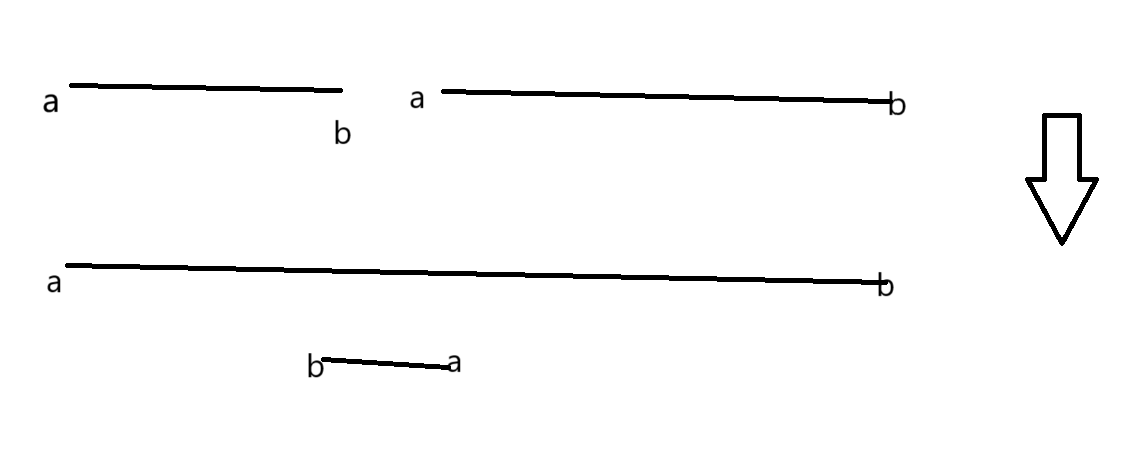
如图，进行一次操作后，可以增加一个区间的两倍。考虑 \(l_i=\min(a_i,b_i),r_i=\max(a_i,b_i)\)，此时对于任意 \(1\le i,j\le n\)，可以交换 \(b_i,b_j\) 使得绝对值总和增加 \(2\times(l_i-r_j)\)。当然，当 \(l_i\le r_j\) 时，由贪心思路，此时不交换，因为交换增加不了收益。
所以，按照贪心，我们选择最大的一个 \(l_i\) 和最小的一个 \(r_j\)，进行操作。当然要与 \(0\) 取最大，以免造成负面收益。
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int N = 2e5+9;
int t,n,a[N],b[N];
signed main()
{
cin >> t;
while (t--)
{
cin >> n;
for (int i = 1; i <= n; ++i) cin >> a[i];
for (int i = 1; i <= n; ++i) cin >> b[i];
int minn = 1e+9,maxx = 0,sum = 0;
for (int i = 1; i <= n; ++i)
{
minn = min(minn, max(a[i], b[i]));
maxx = max(maxx, min(a[i], b[i]));
sum += abs(a[i] - b[i]);
}
cout << sum + max(0LL, (maxx - minn) * 2) << endl;
}
return 0;
}
CF1949B Charming Meals
题意：有两个数组 \(a\) 和 \(b\)，可以任意交换进行匹配，最大化\(\min_{i=1}^{n} |a_i-b_i|\)。
首先看到最小值最大，可以考虑二分。
结论性的，把所有配对分为 \(a<b\) 和 \(a>b\) 两类，那么每一类内部肯定都是顺次匹配。换句话说，最优解就是将 \(a\) 的一个前缀和 \(b\) 等长的后缀顺次匹配，再将 \(a\) 剩余的后缀和 \(b\) 剩余的前缀顺次匹配。关键就是要寻找这个断点，暴力枚举取答案即可做到 \(\mathcal{O}(n^2)\)。
考虑优化，二分答案，再二分前缀长度看这个前缀是否可以满足答案的需求，找出满足需求的最长前缀，在此基础上再看后缀是否合法，即可判定答案是否合法，从而加速到 \(\mathcal{O}(n\log^2V)\)。
- 二分做法 \(\mathcal{O}(n\log^2V)\)
#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define ull unsigned long long
#define debug(...) fprintf(stderr,__VA_ARGS__)
inline ll read() {
ll x(0),f(1);
char c=getchar();
while(!isdigit(c)) {
if(c=='-')f=-1;
c=getchar();
}
while(isdigit(c)) {
x=(x<<1)+(x<<3)+c-'0';
c=getchar();
}
return x*f;
}
const int N=5050;
const int M=8e6+100;
const int mod=1e9+7;
int n;
int a[N],b[N];
bool calc1(int p,int w){//判断p对红色合法
for(int i=1;i<=p;i++){
if(b[n-p+i]-a[i]<w) return false;
}
return true;
}
bool calc2(int p,int w){//判断p对蓝色是否合法
for(int i=p+1;i<=n;i++){
if(a[i]-b[i-p]<w) return false;
}
return true;
}
bool check(int w){
int st=0,ed=n;
while(st<ed){
int mid=(st+ed+1)>>1;
if(calc1(mid,w)) st=mid;
else ed=mid-1;
}//二分找到一个最大的让红色合法的位置p
return calc2(st,w);//判断是否能让蓝色合法
}
signed main() {
int T=read();
while(T--){
n=read();
for(int i=1;i<=n;i++) a[i]=read();
for(int i=1;i<=n;i++) b[i]=read();
sort(a+1,a+1+n);
sort(b+1,b+1+n);
int st=0,ed=1e9;
while(st<ed){//二分答案
int mid=(st+ed+1)>>1;
if(check(mid)) st=mid;
else ed=mid-1;
}
printf("%d\n",st);
}
}
- 贪心做法 \(\mathcal{O}(n^2)\)
#include<bits/stdc++.h>
using namespace std;
int t,n,a[100010],b[100010];
void solve(){
cin>>n;
for(int i=1;i<=n;i++) cin>>a[i];
for(int i=1;i<=n;i++) cin>>b[i];
sort(a+1,a+n+1);
sort(b+1,b+n+1); // 排序
int ans=0;
for(int i=1;i<=n;i++){ // 枚举折点
int tmp=INT_MAX;
for(int j=1;j<=i;j++)
tmp=min(tmp,abs(a[j]-b[n-i+j]));
for(int j=i+1;j<=n;j++)
tmp=min(tmp,abs(a[j]-b[j-i]));
ans=max(ans,tmp);
}
cout<<ans<<endl;
}
signed main(){
cin>>t;
while(t--)
solve();
return 0;
}
CF2018B Speedbreaker
策略 \(\text{X}\)：按 \(a_i\) 排序，每次选择 \(a_i\) 最小的并向它扩展。（CSP-S2023 种树）
这个策略一定是正确的，证明可以考虑交换论证。
解一定是一段区间。
证明：
假设 \(x < y < z\) 且 \(x,\,z\) 满足条件而 \(y\) 不满足条件。不妨设 \(u\) 是那个 \(y\) 走不到的点。若 \(u < y\) 则等到 \(z\) 扩展到 \(y\) 的时候显然走不到 \(u\) 了，否则 \(x\) 走不到 \(u\)。
接下来我们给出断言：如果有解，则答案就是 \([i - a_i + 1,\,i + a_i - 1]\) 区间的交。
必要性显然，充分性考虑对其施策略 \(\text{X}\)，失效当且仅当对于 \(a_i\) 相同的点它们的最远距离大于 \(a_i\) 了。（这种情况显然无解）
于是无解的情况和答案就讨论好了。
#include <bits/stdc++.h>
#define X first
#define Y second
#define rep(i, a, b) for (int i = a; i <= b; i++)
#define per(i, a, b) for (int i = a; i >= b; i--)
#define pb push_back
using namespace std;
typedef long long int ll;
using pii = pair<int, int>;
const int maxn = 5e5 + 10, mod = 1e9 + 7;
int T, n; vector<int> e[maxn];
int main() {
scanf("%d", &T);
while (T--) {
scanf("%d", &n); int l = 1, r = n, L = n + 1, R = 0, fg = 1;
for (int i = 1, x; i <= n; i++) scanf("%d", &x), l = max(l, i - x + 1), r = min(r, i + x - 1), e[x].pb(i);
for (int i = 1; i <= n; i++) {
for (int x : e[i]) L = min(L, x), R = max(R, x); e[i].clear();
if (R - L + 1 > i) fg = 0;
}
if (fg && l <= r) printf("%d\n", r - l + 1);
else puts("0");
}
return 0;
}
CF1875D Jellyfish and Mex
首先求出原有的 \(\text {mex}\)，高于 \(\text{mex}\) 的数一定不用考虑。先分析一下：如果把 \(0\) 删完，那么 \(\text{mex}\) 就一直是 \(0\) 了。但在删 \(0\) 之前可能需要先删一些更大的数使得 \(\text{mex}\) 暂时更小一点。删数一定是要么不删要么删空，且一定是从大到小删。
设计 \(f_i\) 表示把 \(i\) 删空时代价的最小值，枚举上一个删除的数字 \(j\)，则有转移 \(f_i ←f_j + (\text{cnt}_i − 1) \times j + i\)。
暴力转移即可，时间复杂度 \(\mathcal{O}(n^2)\) 。
#include<bits/stdc++.h>
#define int long long
using namespace std;
int T, n;
map<int,int> cnt;
int dp[5005];
signed main() {
ios :: sync_with_stdio(false);
cin >> T;
while (T--) {
cin >> n;
cnt.clear();
memset(dp, 0x3f, sizeof(dp));
for (int i = 1, tmp; i <= n; i++) {
cin >> tmp;
cnt[tmp]++;
}
int mex = 0;
while (cnt[mex]) mex++;
dp[mex] = 0;
for (int i = mex; i >= 1; i--) {
for (int j = 0; j < i; j++) {
dp[j] = min(dp[j], dp[i] + (cnt[j] - 1) * i + j);
}
}
cout << dp[0] << endl;
}
return 0;
}
CF2057D Gifts Order
注意到，最优的区间一定会使最大值和最小值分别取在区间的两个端点，否则缩小区间一定更优。
因此可以看成选择 \(l,r\)，最大化 \(a_r − a_l − (r − l),\ a_l − a_r − (r − l)\)。
建立线段树，维护区间内最大的 \(a_r − r, −a_r − r, a_l + l, −a_l + l\)，合并两个区间时，答案可能在两个区间内部（直接从左右儿子取 \(\max\) 即可），或者来自跨过区间的 \(l，r\)。对于跨过区间的 \(l,r\)，尝试将左区间最大的 \(a_l + l\) 和右区间最大的 \(−a_r − r\) 拼在一起向答案作贡献即可；另一种情况则是将左区间最大的 \(−a_l + l\) 和右区间最大的 \(a_r − r\) 拼在一起向答案作贡献。
单点修改自然就很简单了。时间复杂度 \(\mathcal{O}(n \log n)\)。
#include<bits/stdc++.h>
#define int long long
#define lr (ro*2)
#define rr (ro*2+1)
#define mid ((l+r)/2)
using namespace std;
const int N=1e6;
int a[N];
int n,q;
// 线段树节点结构体，包含最大值、最小值和答案
struct node
{
int max1,min1; // max1和min1分别表示a[i]+i的最大值和最小值
int max2,min2; // max2和min2分别表示a[i]-i的最大值和最小值
int ans1,ans2; // ans1和ans2分别表示两种情况下的最大便利值
};
node tr[N*4];
// 线段树的push_up操作，用于更新父节点的值
void push_up(int ro){
// 更新当前节点的max1和min1
tr[ro].max1=max(tr[lr].max1,tr[rr].max1);
tr[ro].min1=min(tr[lr].min1,tr[rr].min1);
// 更新当前节点的max2和min2
tr[ro].max2=max(tr[lr].max2,tr[rr].max2);
tr[ro].min2=min(tr[lr].min2,tr[rr].min2);
// 更新当前节点的ans1和ans2
tr[ro].ans1=max({tr[lr].ans1,tr[rr].ans1,tr[lr].max1-tr[rr].min1});
tr[ro].ans2=max({tr[lr].ans2,tr[rr].ans2,tr[rr].max2-tr[lr].min2});
}
// 线段树的build操作，用于构建线段树
void build(int ro=1,int l=1,int r=n){
if(l==r){
// 叶子节点初始化
tr[ro].max1=tr[ro].min1=a[l]+l;
tr[ro].max2=tr[ro].min2=a[l]-l;
tr[ro].ans1=tr[ro].ans2=0;
return;
}
// 递归构建左右子树
build(lr,l,mid);
build(rr,mid+1,r);
// 更新当前节点
push_up(ro);
}
// 线段树的update操作，用于更新节点值
void update(int x,int d,int ro=1,int l=1,int r=n){
if(l==r){
// 更新叶子节点
tr[ro].max1=tr[ro].min1=d+x;
tr[ro].max2=tr[ro].min2=d-x;
tr[ro].ans1=tr[ro].ans2=0;
return;
}
// 递归更新左右子树
if(x<=mid)
update(x,d,lr,l,mid);
else
update(x,d,rr,mid+1,r);
// 更新当前节点
push_up(ro);
}
// 主函数，处理多个测试用例
signed main(){
int T;
cin>>T;
while (T--)
{
cin>>n>>q;
for(int i=1;i<=n;i++){
cin>>a[i];
}
// 构建线段树
build();
// 输出初始的最大便利值
cout<<max(tr[1].ans1,tr[1].ans2)<<endl;
while (q--)
{
int p,x;
cin>>p>>x;
// 更新线段树
update(p,x);
// 输出更新后的最大便利值
cout<<max(tr[1].ans1,tr[1].ans2)<<endl;
}
}
}
浙公网安备 33010602011771号