【知识】四边形不等式

大佬博客

四边形不等式

定义：

对于二维函数 \(W\) 中满足 \(a \leq b \leq c \leq d \ \ a,b,c,d \in Z\) 都有 \(W_{a,d} + W_{b, c} \geq W_{a, c} + W_{b, d}\)，则称 \(W\) 满足足四边形不等式。

性质：

满足 \(\forall i < i + 1 \leq j < j + 1 \ \ i,j\in Z\)， \(W_{i, j + 1} + W_{i + 1, j} \geq W_{i, j} + W_{i + 1, j+1} \ \ ①\)，那么 \(W\) 满足四边形不等式。

证明：

  • 取 \(i + 1 < i + 2 \leq j < j + 1\)

    令 \(i^{'} = i + 1\)，则有

    \(W_{{i^{'}},j+1} + W_{{i^{'}+1},j} \geq W_{{i^{'},j}} + W_{{i^{'}+1,j+1}}\)

    即 \(W_{i+1, j + 1} + W_{i + 2, j} \geq W_{i + 1, j} + W_{i + 2, j + 1} \ \ ②\)

    \(①+② \ \ W_{i,j+1} + W_{i + 1, j} + W_{i+1,j+1} + W_{i+2, j} \geq W_{i,j}+W_{i+1,j+1}+W_{i+1,j}+W_{i+2,j+1}\)

    整理可得，\(W_{i, j+1} + W_{i + 2, j} \geq W_{i, j} + W_{i + 2, j + 1}\)

  • 取 \(i+2<i+3 \leq j < j + 1\)

    同理可得， \(W_{i, j + 1} + W_{i + 3, j} \geq W_{i, j} + W_{i + 3, j + 1}\)

所以 ：\(\forall a \leq b \leq c < c + 1,\ \ a,b,c \in Z\)，都有 \(W_{a, c+1} + W_{b, c} \geq W_{a, c} + W_{b, c + 1} \ \ ③\)

  • 取 \(a \leq b \leq c + 1 < c + 2\)

    则 \(W_{a, c+2} + W_{b, c+1} \geq W_{a, c+1} + W_{b, c + 2} \ \ ④\)

    \(③+④ \ \ W_{a, c+1} + W_{b, c} + W_{a, c+2} + W_{b, c+1} \geq W_{a, c} + W_{b, c + 1} + W_{a, c+1} + W_{b, c + 2}\)

    整理可得， \(W_{b, c} + W_{a, c+2} \geq W_{a, c} + W_{b, c + 2}\)

  • 取 \(a \leq b \leq c + 2 < c + 3\)

    同理可得， \(W_{b, c} + W_{a, c + 3} \geq W_{a, c} + W_{b, c + 3}\)

所以：\(\forall a \leq b \leq c \leq d\)，都有 \(W_{a, d} + W_{b, c} \geq W_{a, c} + W_{b, d}\)

证毕！

为啥叫四边形不等式呢？如下图
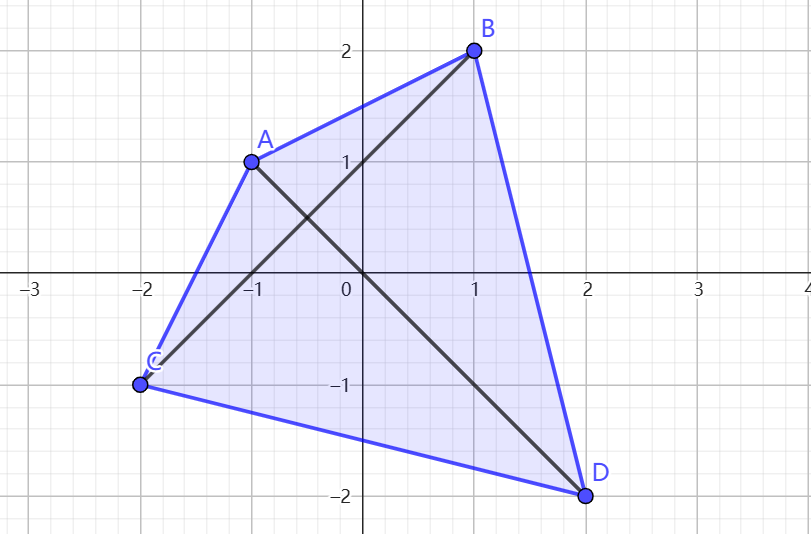
image

易证 \(AD + BC \ge AC + BD\)

DP 优化：

考虑一种决策型动态规划问题，其状态转移方程如下：

\[f_i = \min \limits _{0 \leq j < i} \left\{ f_j + v_{j,i} \right\}. \]

这种形式的转移方程通常出现在以下类型的问题中：给定 \(n\) 个数，需要将它们分成若干连续的区间，并且每个区间都有一个特定的价值，目标是最小化所有区间价值之和。我们令 \(f_i\) 表示将前 \(i\) 个数分成若干段后的最小总价值，枚举 \(j\) 就是决定第 \(i\) 个数属于哪一段，而 \(v_{j,i}\) 则表示这一段的总价值。

为了优化这个问题，引入决策点的概念。我们定义 \(p_i\) 为一个决策点，它是对于每个 \(i\)，在 \(0 \leq j < i\) 的范围内，使得 \(f_j + v_{j,i}\) 达到最小值的 \(j\)。因此，\(p_i\) 就是 \(i\) 的决策点。

对于这类问题，一般的做法是直接采用朴素的 \(\mathcal{O}(n^2)\) 时间复杂度算法。然而，若 \(v\) 满足四边形不等式，我们可以通过以下方法来优化计算过程。

Property 1：

如果 \(v\) 满足四边形不等式，那么每个 \(i\) 的决策点是单调递增的。

Property 2：

如果存在一个 \(x < j\)，使得对于某个 \(i > j\)，选取 \(j\) 的转移比选取 \(x\) 更优，那么对于所有 \(i' > i\)，选择 \(j\) 也将比选择 \(x\) 更优。实际上，\(j\) 作为 \(i\) 的决策点与性质 1 是等价的，而性质 1 实际上是性质 2 的一个特殊情况。

特别要注意的是，\(x\) 必须满足 \(x < j\)。

证明：

由于 \(j\) 比 \(x\) 对 \(i\) 的贡献更优，所以我们有：

\[f_j + v_{j, i} \leq f_x + v_{x, i}. \]

同时，由于 \(v\) 满足四边形不等式，意味着：

\[v_{x, i'} + v_{j, i} \geq v_{x, i} + v_{j, i'}, \]

这可以推导出：

\[v_{j, i'} - v_{j, i} \leq v_{x, i'} - v_{x, i}. \]

将上述不等式与原不等式相加，得到：

\[f_j + v_{j, i'} \leq f_x + v_{x, i'}. \]

如何优化 DP ？

首先，我们设定初始时每个 \(i\) 的决策点都为 \(0\)，然后从前往后依次计算每个 \(f_i\)，并尝试用当前的 \(i\) 作为新的决策点来更新其他的状态。

基于性质 2，如果某个 \(f_i\) 能更新 \(f_x\)，那么它同样能够更新从 \(f_{x+1}\) 到 \(f_n\)。也就是说，\(f_i\) 能更新的点总是处于一个连续的尾段。我们可以通过二分法来高效地找到这个更新区间。

为了进一步优化，我们可以维护一个单调队列，其中每个元素表示一个三元组 \((l, r, c)\)，其中 \(l \sim r\) 表示在区间 \([l, r]\) 内，每个点的最优决策都是 \(c\)。我们通过这个队列可以高效地找到 \(p\) 的位置。对于每个 \(i\)，我们先从队列中找到该位置 \(p\) 的区间，然后在 \([l, r]\) 区间内二分查找更新的决策点，并相应更新队列。

另外，也可以采用分治法来进行优化，这样的时间复杂度同样是 \(\mathcal{O}(n \log n)\)。

题目梳理：

  • P3195 [HNOI2008]玩具装箱

    考虑一个 \(\mathcal{O}(n^2)\) 的 dp。

    设 \(f_i\) 表示前 \(i\) 个玩具的最小总费用，\(s_i\) 表示前 \(i\) 个玩具的长度和，即前缀和。

    有转移方程：\(f_i = \min \limits_{0 \leq j < i} \{f_j + (s_i-s_j+i-j-1-l)^2\}\)。在这题中前文的 \(v\) 即后面的 \((s_i-s_j+i-j-1-l)^2\)，我们只需要证明 v 满足四边形不等式即可。

    \(证明：设\) \(Q=S[i]-S[j]-1-L\)

    \(\therefore w(i,j)=(S[i]-S[j]-1-L)^2=Q^2\)

    $\therefore w(i+1,j+1)=(S[i+1]-S[j+1]-1-L)^2\ =((S[i]+C[i+1]+1)-(S[j]+C[j+1]+1)-1-L)^2\ =(Q+C[i+1]-C[j+1])^2 $

    \(w(i,j+1)=(S[i]-S[j+1]-1-L)^2\\ =(S[i]-(S[j]+C[j+1]+1)-1-L)^2\\ =(Q-C[j+1]-1)^2\)

    \(w(i+1,j)=(S[i+1]-S[j]-1-L)^2\\ =((S[i]+C[i+1]+1)-S[j]-1-L)^2\\ =(Q+C[i+1]+1)^2\)

    \(\therefore w(i,j)+w(i+1,j+1)=2Q^2+2C[i+1]Q-2C[j+1]Q+C[i+1]^2-2C[i+1]C[j+1]+C[j+1]^2\)

    \(\therefore w(i+1,j)+w(i,j+1)=2Q^2+2C[i+1]Q-2C[j+1]Q+C[i+1]^2+2C[i+1]+2C[j+1]+C[j+1]^2+2\) $\therefore w(i,j)+w(i+1,j+1)-w(i+1,j)+w(i,j+1)=-2(C[i+1]+1)(C[j+1]+1) $

    \(\text{又} \because C[i],C[j] \geqslant 1 \therefore -2(C[i+1]+1)(C[j+1]+1) \leqslant -8\)

    $ \therefore w(i,j)+w(i+1,j+1) \leqslant w(i+1,j)+w(i,j+1)$

    Code 
    #include <bits/stdc++.h>
using namespace std;
#define int long long
const int MAXN = 50050;
int N, L, dp[MAXN], sum[MAXN], f[MAXN], g[MAXN], h, t, Q[MAXN];
inline double calc(int j1, int j2){
	return (double) (dp[j2] + g[j2] - dp[j1] - g[j1]) / (f[j2] - f[j1]);
}
#undef int
int main(){
	cin >> N >> L;
	for(int i = 1; i <= N; i++)
	{
		cin >> sum[i];
		sum[i] += sum[i - 1];
		f[i] = sum[i] + i;
		g[i] = (f[i] + L + 1) * (f[i] + L + 1);
	}
	g[0] = (L + 1) * (L + 1); 
	for(int i = 1; i <= N; i++){
		while(h < t && calc(Q[h], Q[h + 1]) <= 2 * f[i]) h++;
		dp[i] = dp[Q[h]] + (f[i] - f[Q[h]] - L - 1) * (f[i] - f[Q[h]] - L - 1); 
		while(h < t && calc(Q[t], i) < calc(Q[t - 1], Q[t])) t--;
		Q[++t] = i;

	}
	cout << dp[N];
	return 0;
}

  • P1912 [NOI2009] 诗人小G

    很显然的 dp 方程：

    \[f_i=\min(f_j+|\text{sum}_i-\text{sum}_j+i-j-1-L|^P) \]

    其中

    \[\text{sum}_x=\sum_{i=1}^xa_i \]

    如果这个状态转移方程是决策单调的，那么可以直接上单调队列。

    但是怎么证明呢？

    我们只需证明函数\(G_j(i)=|\text{sum}_i+i-(\text{sum}_j+j)-(1+L)|^P\)满足四边形不等式。

    \[\Leftrightarrow\ G_j(i+1)+G_{j+1}(i)\geq G_{j}(i)+G_{j+1}(i+1) \]

    尝试把左右两边统一化，简化式子，表示 \(G_{j},G_{j+1}\)

    设

    \[u=\text{sum}_i+i-(\text{sum}_j+j)-(1+L),v=\text{sum}_i+i-(\text{sum}_j+a[j]+j+1)-(1+L) \]

    则

    \[\Leftrightarrow |u+1+a_{i+1}|^P+|v|^P\geq |u|^P+|v+1+a_{i+1}|^P \]

    \[\Leftrightarrow |v|^P-|v+a_{i+1}+1|^P\geq |u|^P-|u+a_{i+1}+1|^P \]

    \[\because\ u>v \]

    所以原问题等价于证明 \(h(x)=|x|^P-|x+z|^P(z\in [0,\infty))\) 非严格单调递减。

    注意到有绝对值，我们分类讨论。

    当 \(x\in[0,\infty):\)

    \[h(x)=x^P-(x+z)^P \]

    \[h'(x) =Px^{P-1}-P(x+z)^{P-1} \]

    \[=Px^{P-1}-P\sum_{i=0}^{P-1}C_{P-1}^ix^{P-i-1}z^i $$=-P\sum_{i=1}^{P-1}C_{P-1}^ix^{P-i-1}z^i\]

    由于 \(z\geq 0,x\in[0,\infty),\therefore h'(x)\leq0,\text{Q.E.D.}\)

    当 $x\in(-\infty,0),P\equiv0\pmod 2: $

    \[h(x)=x^P-(x+z)^P \]

    证明过程同第一种情况，此处省略。

    当 \(x\in[-z,0),P\equiv1\pmod 2:\)

    \[h(x)=-x^P-(x+z)^P \]

    \[h'(x)=-Px^{P-1}-P(x+z)^{P-1} \]

    由于 \(x^{P-1}\) 恒大于 \(0\)，$$\therefore h'(x)\leq0,\text{Q.E.D.}$$

    当 \(x\in(-\infty,-z),P\equiv1\pmod 2:\)

    \[h(x)=-x^P+(x+z)^P \]

    \[h'(x)=-Px^{P-1}+P(x+z)^{P-1} \]

    \[h'(x)=-P(x^{P-1}-(x+z)^{P-1}) \]

    显然 \(x^{P-1}>(x+z)^{P-1}\)，因为这是一个偶函数。

    所以 \(h'(x)\leq 0,\text{Q.E.D.}\)

    Code 
    #include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

typedef long double LD;
const int N = 100010;

int n, L, P;
LD f[N];
char str[N][31];
int s[N], opt[N];
struct Node
{
	int j, l, r;
}q[N];
int hh, tt;

LD val(int j, int i)
{
	LD res = 1, a = abs(s[i] - s[j] + i - j - 1 - L);
	for (int i = 0; i < P; i ++ ) res *= a;
	return res + f[j];
}

void insert(int i)
{
	int pos = n + 1;
	while (hh <= tt && val(q[tt].j, q[tt].l) >= val(i, q[tt].l)) pos = q[tt -- ].l;
	if (hh <= tt && val(q[tt].j, q[tt].r) >= val(i, q[tt].r))
	{
		int l = q[tt].l, r = q[tt].r;
		while (l < r)
		{
			int mid = l + r >> 1;
			if (val(q[tt].j, mid) >= val(i, mid)) r = mid;
			else l = mid + 1;
		}
		q[tt].r = r - 1;
		pos = r;
	}
	if (pos != n + 1) q[ ++ tt] = {i, pos, n};
}

int main()
{
	int T;
	scanf("%d", &T);
	while (T -- )
	{
		scanf("%d%d%d", &n, &L, &P);
		for (int i = n; i >= 1; i -- ) scanf("%s", str[i]);
		for (int i = 1; i <= n; i ++ ) s[i] = s[i - 1] + strlen(str[i]);
		hh = tt = 0;
		q[0] = {0, 1, n};
		for (int i = 1; i <= n; i ++ )
		{
			f[i] = val(q[hh].j, i), opt[i] = q[hh].j;
			if (q[hh].r == i) hh ++ ;
			q[hh].l = i + 1;
			insert(i);
		}

		if (f[n] > 1e18) puts("Too hard to arrange");
		else
		{
			printf("%lld\n", (long long)f[n]);
			for (int i = n; i; i = opt[i])
			{
				for (int j = i; j > opt[i]; j -- )
				{
					printf("%s", str[j]);
					if (j != opt[i] + 1) printf(" ");
				}
				puts("");
			}
		}
		puts("--------------------");
	}

	return 0;
}
posted @ 2024-12-07 14:52  Star_F  阅读(23)  评论(0)  编辑  收藏  举报