Dijkstra（迪杰斯特拉）算法的演示与理解证明

图片来自《我的第一本算法书》（书中 Dijkstra 译作狄克斯特拉）

1、Dijkstra 算法的演示

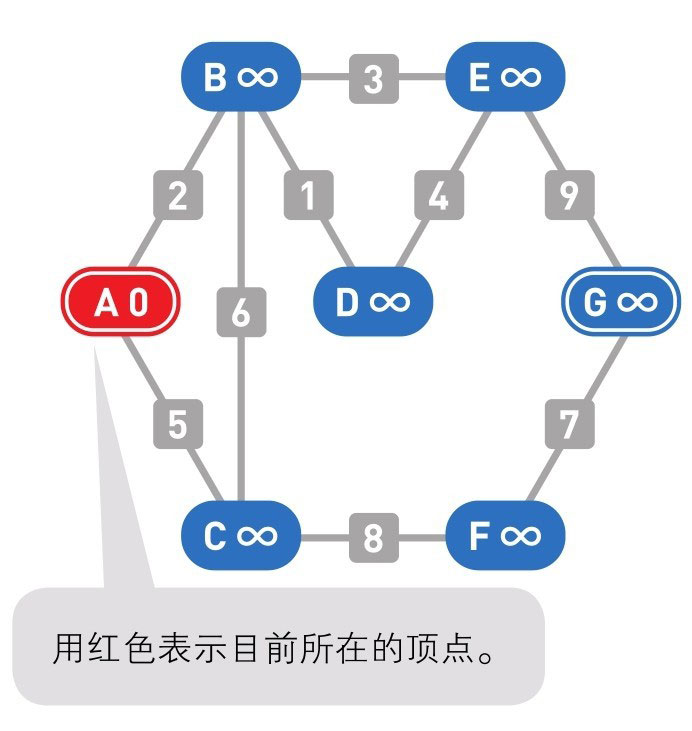
我们设 A 为起点，G 为终点。演示用的图是无向带权图。

然后设置各个顶点的初始权重：起点为 0，其他顶点为无穷大（∞）。（注：这里的每个点的权重，即从 A 点到该点的最短距离）

下面的颜色中，红色表示目前所在的顶点，绿色表示候补顶点，橙色表示已经确定了最小权重的顶点（红色的顶点当然也确定了最小权重，它将在下一步变更为橙色）

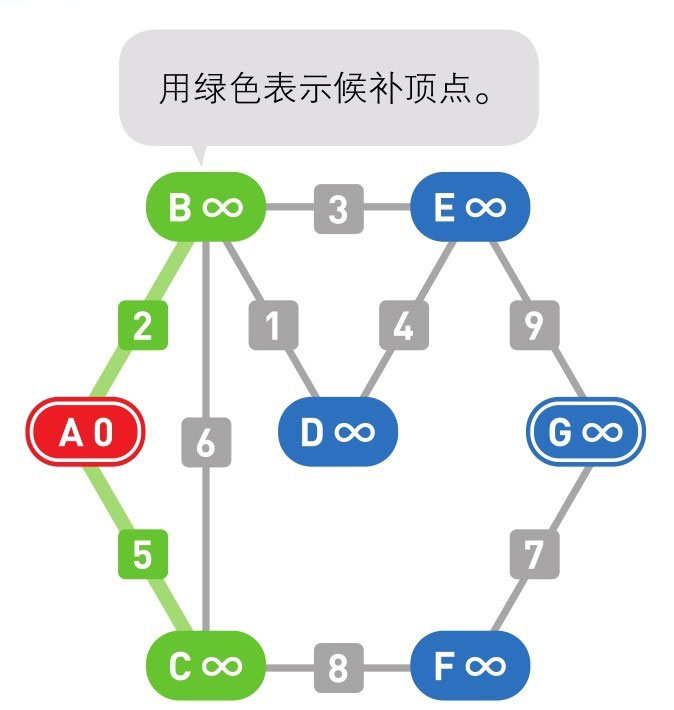
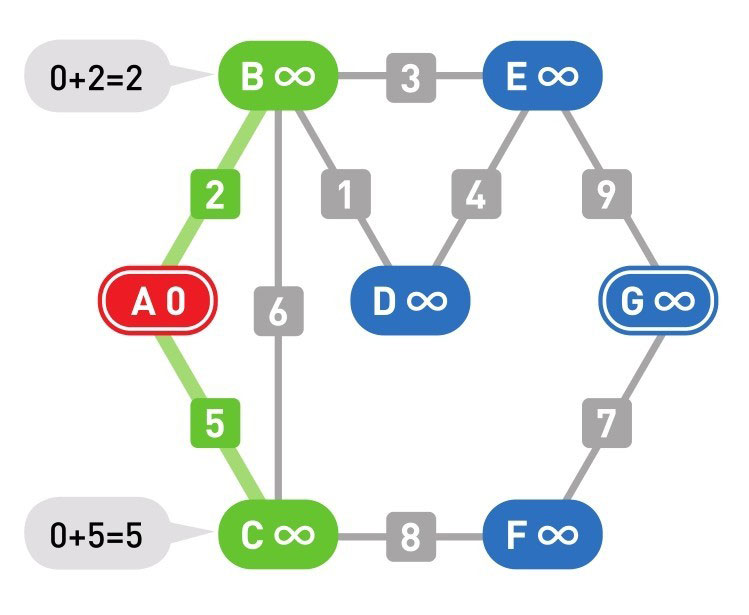
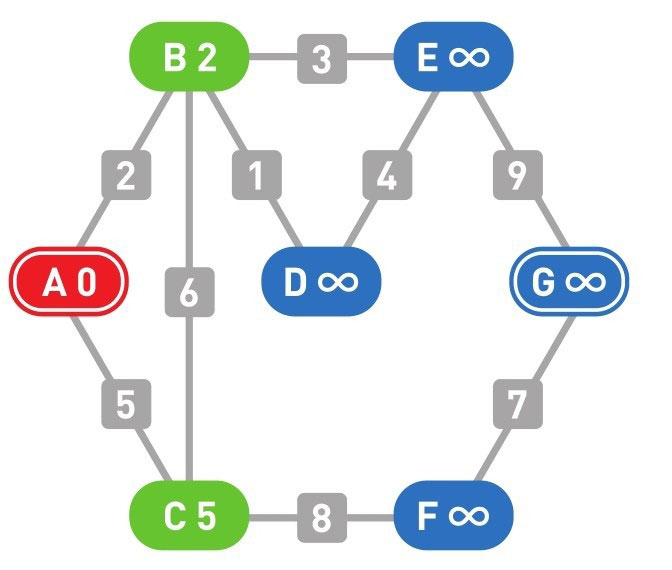
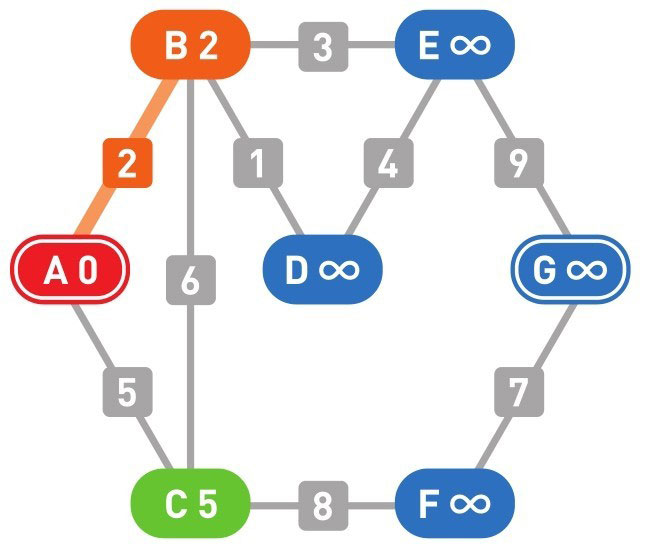
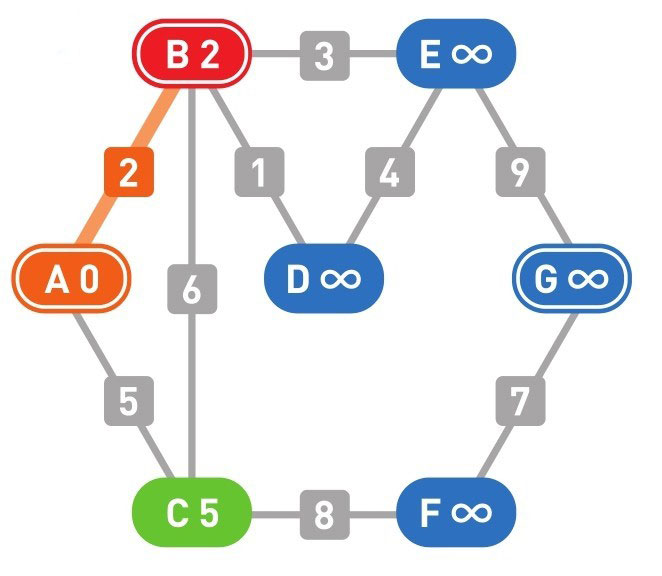
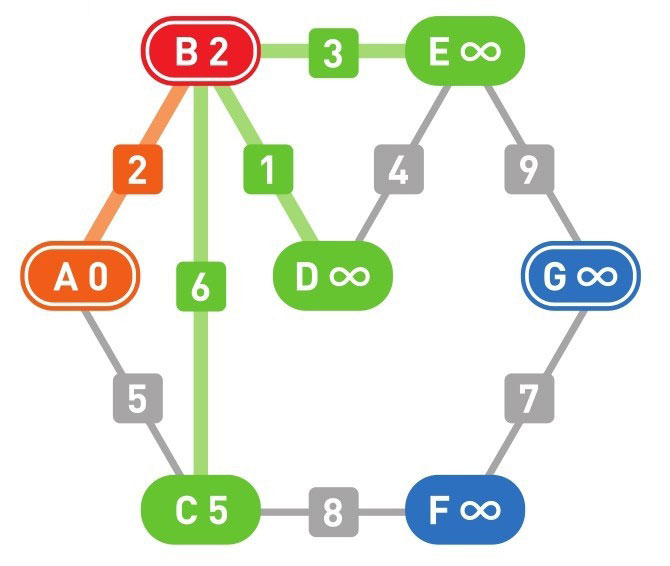
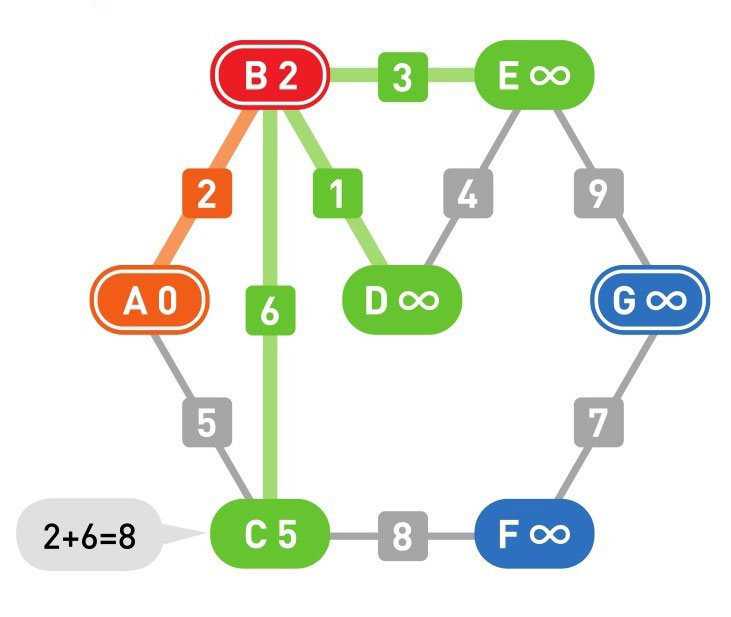
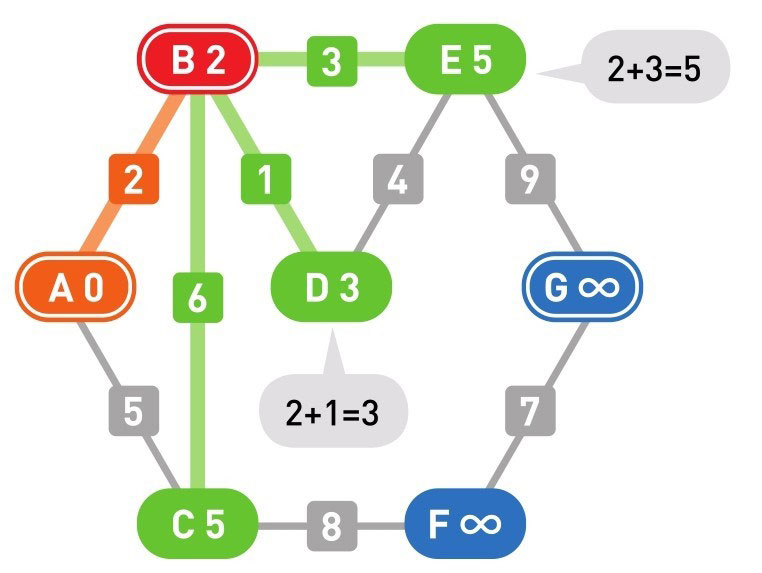
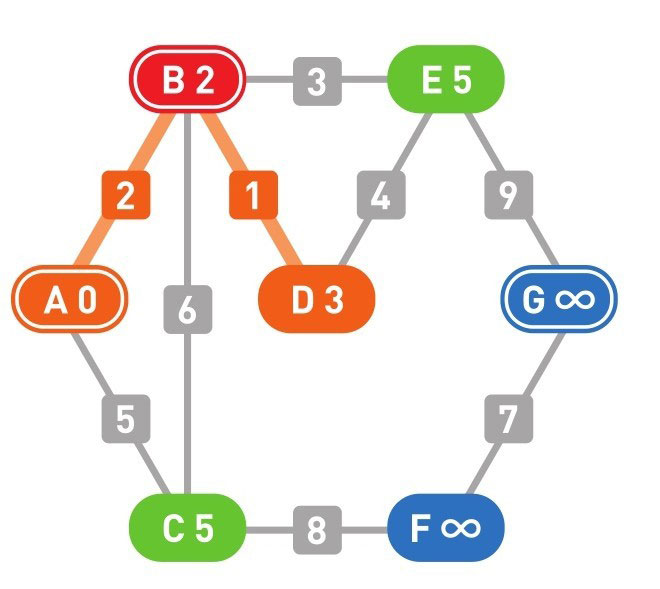
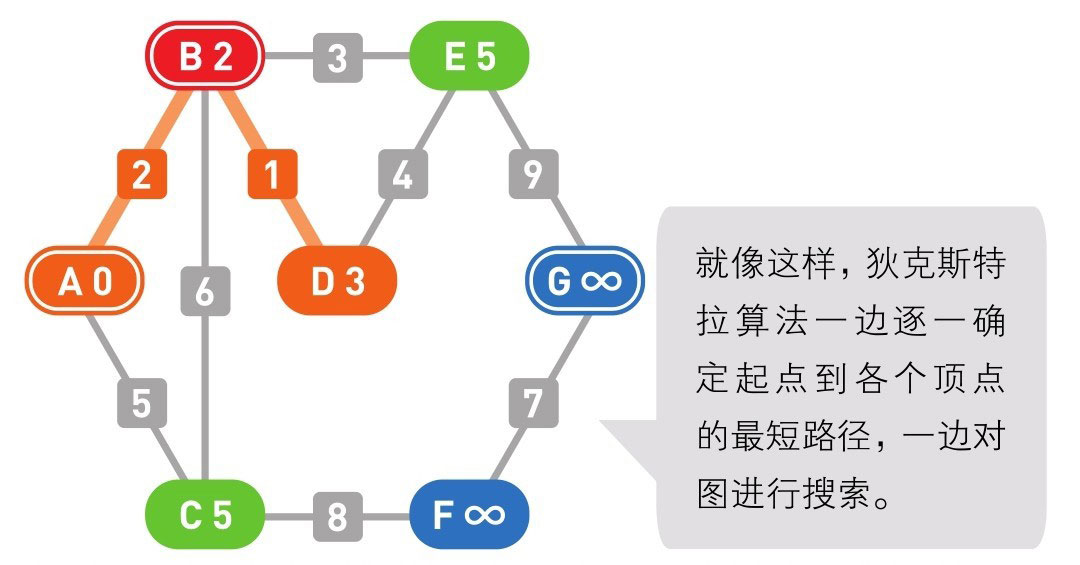
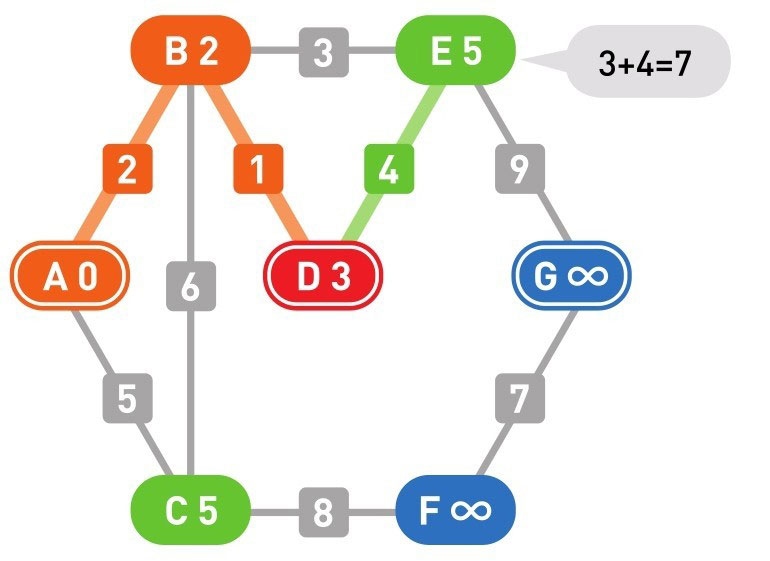
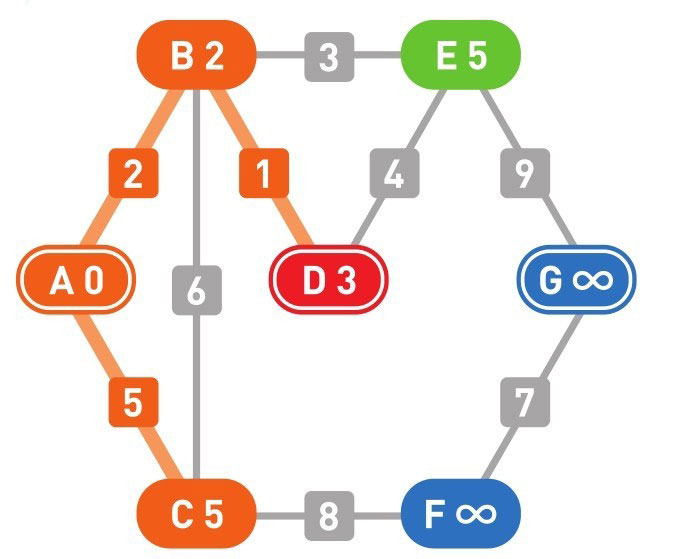
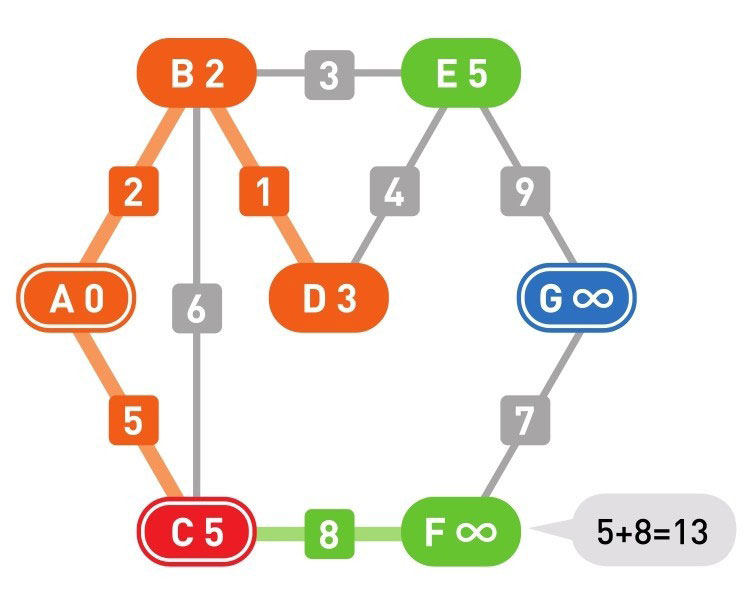
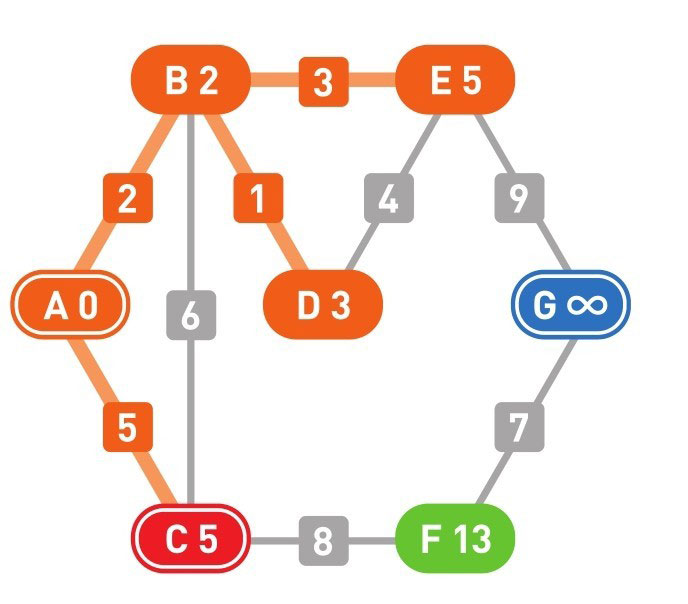
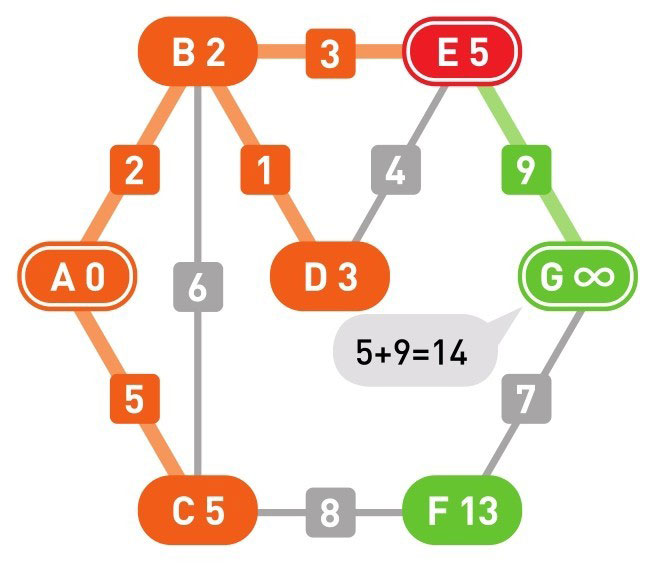
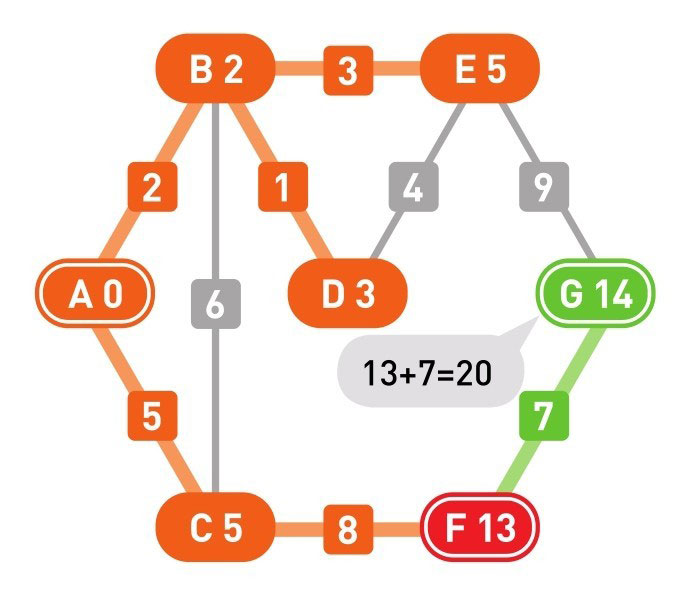
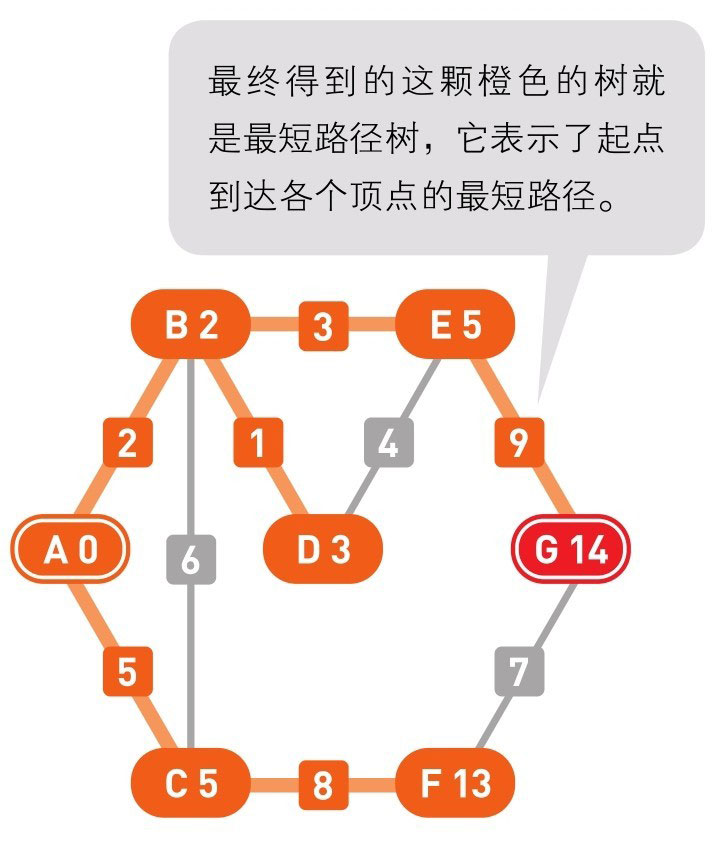
到这里（上面的最后一幅图），已经到达了终点 G，搜索结束。

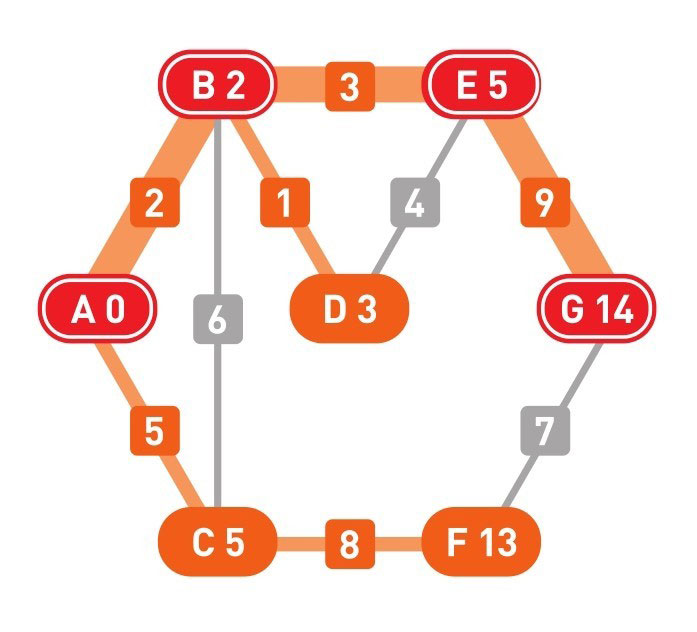
上面的用红色的节点表示从 A 点到达 G 点的最短路径经过的节点。

2、证明

先给出浙江大学陈越教授编写的教材上（《数据结构 第 2 版》）给的证明。

书中用的图是这样的：

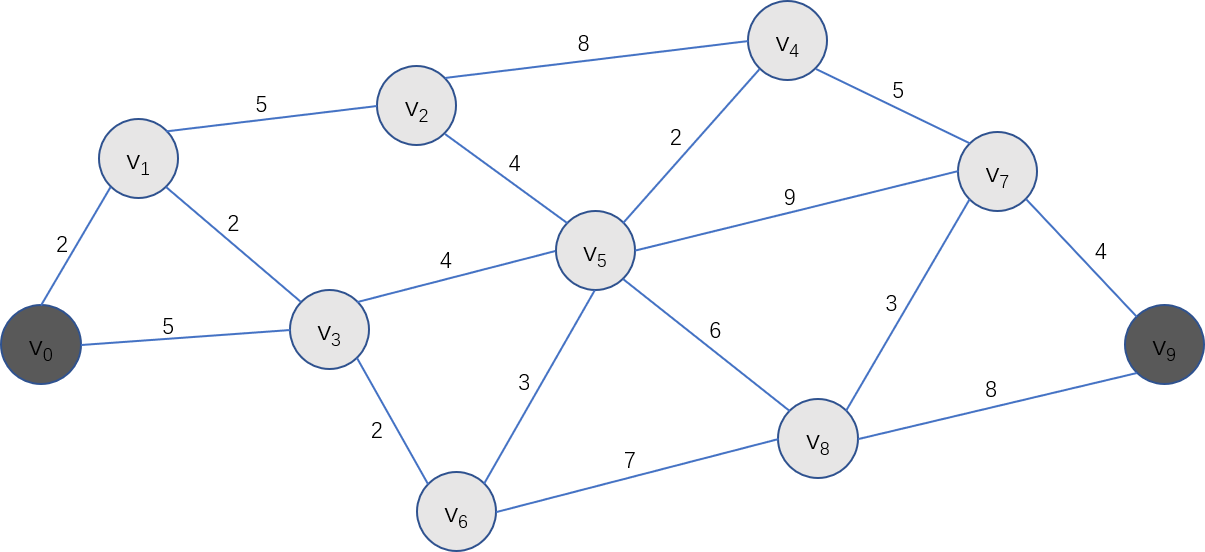
其实只是把之前演示的图中的 A、B、C、D... 节点换成了 \(v_0, v_1, v_2, v_3...\)，其效果是一样的。

原书对于 Dijkstra 算法的描述：

假设有向图 \(G = \{ V, E \}\)（无向图可以看成所有边都是双向边的有向图），设置两个顶点的集合 \(S\) 和 \(T\)（\(T = V - S\)），集合 \(S\) 中存放已找到最短路径的顶点，集合 \(T\) 存放当前还未找到最短路径的顶点。初始状态时，集合 \(S\) 中只包含源点 \(v_0\)，然后不断从集合 \(T\) 中选取到顶点 \(v_0\) 路径长度最短的顶点 \(u\) 加入到集合 \(S\) 中（① 见下方注释）。集合 \(S\) 每加入一个新的顶点 \(u\)，都要修改剩余顶点的最短路径长度值（这对应上面图解的例子中的权重），集合 \(T\) 中各顶点新的最短路径长度值为原来的最短路径长度值与顶点 \(u\) 的最短路径长度值加上 \(u\) 到该顶点的路径长度值中的较小值。此过程不断重复，直到集合 \(T\) 的顶点全部加入到 \(S\) 中为止。

书中给的证明：

Dijkstra 算法的正确性可以用反证法加以证明。假设下一条最短路径的终点是 v，那么该路径必然或者是弧 \((v_0, v)\)，或者是中间只经过集合 \(S\) 中的顶点而到达顶点 \(v\) 的路径。因此假若此路径上（终点为 \(v\) 的最短路径）除 \(v\) 之外还有一个或一个以上的顶点不在集合 \(S\) 中，那么必然存在另外的终点不在 \(S\) 中而该终点的路径长度比此路径还短的路径，这与我们按路径长度递增的顺序产生最短路径的前提相矛盾，所以此假设不成立。（② 见下方注释）

① 我们选取的时候是这样的，假设我们刚找到从顶点 \(v_0\) 到顶点 \(u\) 的最短路径长度，并把 \(u\) 加入到集合 \(S\) 中，然后我们在从集合 \(T\) 中选取下一个到顶点 \(v_0\) 路径长度最短的顶点之前，我们要先更新 \(T\) 中与 \(u\) 相邻的各个顶点的最短路径长度（最小权重），更新完之后，我们在从所有的 \(T\) 集合中的元素中选取最短路径长度（最小权重）最小的那一个，这便是下一个将加入 \(S\) 中的元素。

② 给这个证明稍微加一点注释。可以很明显地看出来的是，第一个结点（设为 \(p\)）是很容易找到的，只要选取 \(v_0\) 的相邻的结点中到 \(v_0\) 的权重最小的点，弧 \((v_0, p)\) 即 \(v_0\) 到 \(p\) 的最短路径，可以用反证法验证，因为无法找到从 \(v_0\) 开始绕行其他点使得其路径比弧 \((v_0, p)\) 还要短的路径。然后，我们再开始找第二个结点，这个是关键。此时，我们已经将 \(p\) 加入了 \(S\) 中，假设我们可以找到的第二个结点是 \(q\)，我们先更新 \(p\) 的邻接点的最短路径长度（最小权重），那么点 \(q\) 就是 \(T\) 中最短路径距离最小的那一个。这个也是要用反证法来证明。从 \(v_0\) 到 \(p\) 的最短路径，无非有两种情况，一种是假设弧 \((p, v_0)\) 的路径长度比当前寻找到的路径要短，这个与我们之前选取的策略相矛盾，因为如果弧 \((p, v_0)\) 要更小的话，那么在之前的更新中，\(p\) 就不会被更新，也就是说，它的父节点还是 \(v_0\)。另一种就是可以找到不在 \(S\) 中的顶点，那么这个也可以根据上面引用的书中的假设法直接推翻。所以 \(p\) 点的最短路径就找到了，然后顺理成章加入 \(S\)，之后再一步一步地添加相应的节点到 \(S\) 中即可。

其实，关键是要从第二个点就开始仔细想，想一想就明白了其中的原理。

按：我在理解这个算法的证明时，到微信读书上找过许多数据结构的教材来参考，其中，很多国人编写的教材采用的证明竟然和陈越这一版书上的这一小段一模一样，令人惊讶。当然，上下文肯定是不一样的。究竟是谁先谁后呢？不敢妄自揣度。最后只好灰溜溜地回来继续认真阅读陈越这一版的书籍。

3、C 语言实现

本实现来自浙江大学陈越教授编写的《数据结构第 2 版》

#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>
#include <string.h>

/* ******************************************************************************* */
#define MaxVertexNum 100 // 最大顶点数设为 100
#define INFINITY 65535 // 无穷大设为双字节无符号整数的最大值 65535
#define ERROR -1 // 定义错误标记
typedef int Vertex; // 用顶点下标表示顶点, 为整型
typedef int WeightType; // 边的权值设为整型
typedef char DataType; // 顶点存的数据类型设为字符型

// 图节点的定义
typedef struct GNode * PtrToGNode;
struct GNode {
    int Nv; // 顶点数
    int Ne; // 边数
    WeightType G[MaxVertexNum][MaxVertexNum]; // 邻接矩阵
    DataType Data[MaxVertexNum]; // 存顶点的数据
    /* 注意: 若顶点无数据, 此时 Data[] 可以不用出现 */
};
typedef PtrToGNode MGraph;
// 边的定义
typedef struct ENode * PtrToENode;
struct ENode {
    Vertex V1, V2; // 有向边 <v1, V2>
    WeightType Weight; // 权重
};
typedef PtrToENode Edge;

MGraph CreateGraph(int VertexNum)
{
    // 初始化一个有 VertexNum 个顶点但没有边的图
    Vertex V, W;
    MGraph Graph;

    Graph = (MGraph) malloc(sizeof(struct GNode)); // 建立图
    Graph->Nv = VertexNum;
    Graph->Ne = 0;
    // 初始化邻接矩阵
    // 注意: 这里默认顶点编号是从 0 开始, 到 (Graph->Nv - 1)
    for (V = 0; V < Graph->Nv; V++)
        for (W = 0; W < Graph->Nv; W++)
            Graph->G[V][W] = INFINITY;

    return Graph;
}

void InsertEdge(MGraph Graph, Edge E)
{
    // 插入边 <V1, V2>
    Graph->G[E->V1][E->V2] = E->Weight;
    // 若是无向图, 还要插入边 <V2, V1>
    Graph->G[E->V2][E->V1] = E->Weight; // 把无向图的封印给解开
}

MGraph BuildGraph()
{
    MGraph Graph;
    Edge E;
    // Vertex V;
    int Nv, i;

    scanf("%d", &Nv); // 读入顶点个数
    Graph = CreateGraph(Nv); // 初始化有 Nv 个顶点但没有边的图

    scanf("%d", &(Graph->Ne)); // 读入边数
    if (Graph->Ne != 0) // 如果有边
    {
        E = (Edge)malloc(sizeof(struct ENode)); // 建立边节点
        // 读入边, 格式为 "起点 终点 权重", 插入邻接矩阵
        for (i = 0; i < Graph->Ne; i++) {
            scanf("%d %d %d", &E->V1, &E->V2, &E->Weight);
            // 注意: 如果权重不是整型, Weight 的读入格式要改
            InsertEdge(Graph, E);
        }
    }
    // 如果顶点有数据的话, 读入数据
    /*for (V = 0; V < Graph->Nv; V++)
        scanf("%c", &(Graph->Data[V]));*/

    return Graph;
}

// 简单遍历图
void PrintGraph(MGraph G)
{
    int i, j;

    for (i = 0; i < G->Nv; i++)
    {
        for (j = 0; j < G->Nv; j++)
        {
            if (G->G[i][j] == INFINITY)
            {
                printf("∞ ");
                continue;
            }
            printf("%d ", G->G[i][j]);
        }
        printf("\n");
    }
}
/* ******************************************************************************* */
// 上面是使用邻接矩阵表示的图的定义

// Dijkstra 算法
/**
 * 辅助函数，用来寻找未被收录的顶点中的 dist 最小者
 * @param Graph 图
 * @param dist
 * @param collected
 * @return 未被收录顶点中 dist 最小者
 */
Vertex FindMinDist(MGraph Graph, int dist[], bool collected[])
{
    Vertex MinV, V;
    int MinDist = INFINITY;

    for (int V = 0; V < Graph->Nv; V++)
    {
        if (collected[V] == false && dist[V] < MinDist)
        {
            // 若 V 未被收录，且 dist[V] 更小
            MinDist = dist[V]; // 更新最小距离
            MinV = V; // 更新对应顶点
        }
    }
    if (MinDist < INFINITY) // 若找到最小 dist
        return MinV; // 返回对应的顶点下标
    else
        return ERROR; // 若这样的顶点不存在，返回错误标记
}

/**
 * 核心算法
 * @param Graph 待处理的图
 * @param dist 存储最短路径
 * @param path 存储父节点
 * @param S 源点
 * @return true 表示找到，反之则未找到
 */
bool Dijkstra(MGraph Graph, int dist[], int path[], Vertex S)
{
    bool collected[MaxVertexNum]; // true 表示顶点已经求得最短路径
    Vertex V, W;

    // 初始化：此处默认邻接矩阵中不存在的边用 INFINITY 表示
    for (V = 0; V < Graph->Nv; V++)
    {
        dist[V] = Graph->G[S][V];
        if (dist[V] < INFINITY)
            path[V] = S; // 更新父节点
        else
            path[V] = -1; // -1 表示不存在父节点
        collected[V] = false; // 初始时将所有点设为未收集状态
    }
    // 先将起点收入集合
    dist[S] = 0;
    collected[S] = true;

    while (1)
    {
        // V = 未被收录顶点中 dist 最小者
        V = FindMinDist(Graph, dist, collected);
        if (V == ERROR) // 若这样的 V 不存在
            break;
        collected[V] = true; // 收录 V
        // 更新新收录的 V 的邻接点
        for (W = 0; W < Graph->Nv; W++)
            // 若 W 是 V 的邻接点并且未被收录
            if (collected[W] == false && Graph->G[V][W] < INFINITY)
            {
                if (Graph->G[V][W] < 0) // 若有负边。（实际上，这种情况应该是不存在的，因为我们使用 Dijkstra 算法的前提就是假设无负权边）
                    return false; // 不能正确解决，返回错误标记
                // 若收录 V 使得 dist[W] 变小
                if (dist[V] + Graph->G[V][W] < dist[W])
                {
                    dist[W] = dist[V] + Graph->G[V][W]; // 更新 dist[W]
                    path[W] = V;
                }
            }
    } // while 结束
    return true; // 算法执行结束，返回正确标记
}

// 测试一组数据, 测试的图有 5 个顶点, 8 条有向边
// <1, 0, 9> <0, 2, 6> <2, 4, 7> <4, 3, 6> <3, 1, 5> <1, 2, 4> <0, 3, 3> <3, 4, 8>
int dist[MaxVertexNum]; // 这里稍微多申请一些
int path[MaxVertexNum]; // 其实起名叫做 parentNode 或许更合适一些
int main()
{
    MGraph G = BuildGraph();
    // 打印图的邻接矩阵
    PrintGraph(G);
    
    // 给数组分配空间
    memset(dist, 0, sizeof(int) * MaxVertexNum);
    memset(path, 0, sizeof(int) * MaxVertexNum);
    Vertex S = 0; // 源点为 0
    Dijkstra(G, dist, path, S);
    for (int i = 0; i < G->Nv; i++)
    {
        printf("0 号节点到 %d 号节点的最短距离为：%d\n", i, dist[i]);
        printf("%d 号节点的父节点为：%d 号节点\n", i, path[i]);
        printf("*****************\n");
    }

    return 0;
}

// 测试数据
/*
10
17
0 1 2
1 2 5
1 3 2
0 3 5
2 4 8
2 5 4
3 5 4
3 6 2
4 5 2
5 6 3
4 7 5
5 7 9
5 8 6
6 8 7
7 8 3
7 9 4
8 9 8
*/

测试结果：

D:\Users\19833\CLionProjects\Dijkstra\cmake-build-debug\Dijkstra.exe
10
17
0 1 2
1 2 5
1 3 2
0 3 5
2 4 8
2 5 4
3 5 4
3 6 2
4 5 2
5 6 3
4 7 5
5 7 9
5 8 6
6 8 7
7 8 3
7 9 4
8 9 8
∞ 2 ∞ 5 ∞ ∞ ∞ ∞ ∞ ∞ 
2 ∞ 5 2 ∞ ∞ ∞ ∞ ∞ ∞ 
∞ 5 ∞ ∞ 8 4 ∞ ∞ ∞ ∞ 
5 2 ∞ ∞ ∞ 4 2 ∞ ∞ ∞ 
∞ ∞ 8 ∞ ∞ 2 ∞ 5 ∞ ∞ 
∞ ∞ 4 4 2 ∞ 3 9 6 ∞ 
∞ ∞ ∞ 2 ∞ 3 ∞ ∞ 7 ∞ 
∞ ∞ ∞ ∞ 5 9 ∞ ∞ 3 4 
∞ ∞ ∞ ∞ ∞ 6 7 3 ∞ 8 
∞ ∞ ∞ ∞ ∞ ∞ ∞ 4 8 ∞ 
0 号节点到 0 号节点的最短距离为：0
0 号节点的父节点为：-1 号节点
*****************
0 号节点到 1 号节点的最短距离为：2
1 号节点的父节点为：0 号节点
*****************
0 号节点到 2 号节点的最短距离为：7
2 号节点的父节点为：1 号节点
*****************
0 号节点到 3 号节点的最短距离为：4
3 号节点的父节点为：1 号节点
*****************
0 号节点到 4 号节点的最短距离为：10
4 号节点的父节点为：5 号节点
*****************
0 号节点到 5 号节点的最短距离为：8
5 号节点的父节点为：3 号节点
*****************
0 号节点到 6 号节点的最短距离为：6
6 号节点的父节点为：3 号节点
*****************
0 号节点到 7 号节点的最短距离为：15
7 号节点的父节点为：4 号节点
*****************
0 号节点到 8 号节点的最短距离为：13
8 号节点的父节点为：6 号节点
*****************
0 号节点到 9 号节点的最短距离为：19
9 号节点的父节点为：7 号节点
*****************

Process finished with exit code 0

参考：
1、《我的第一本算法书》（宫崎修一 石田保辉）
2、《数据结构 第 2 版》（陈越）