八皇后问题
问题描述
问题描述:在棋盘上放置 8 个皇后,使得它们互不攻击,此时每个皇后的攻击范围为同行同列同对角线,要求找出所有解。
LeetCode上面的描述:
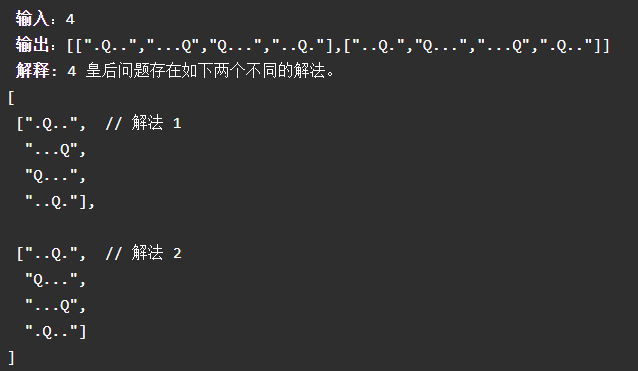
解决方法
这里使用经典的回溯法。
代码:
下面的程序简洁地求解了八皇后问题。在主程序中读入 n,并为 tot 清零,然后调用 search(0),即可得到解的个数 tot。
void search(int cur) { // cur 代表当前行
if (cur == n)
tot++; // 递归边界, 只要走到了这里, 所有皇后必然不冲突, 因为这是从第 8 行(也就是最后一行)递归进来的
else {
for (int i = 0; i < n; i++) { // 对列进行遍历
int ok = 1; // 记录当前的摆放位置是否会和之前已经放好的皇后发生冲突
C[cur] = i;
for (int j = 0; j < cur; j++) { // 检查是否和前面的皇后冲突
if (C[cur] == C[j] || cur - C[cur] == j - C[j] || cur + C[cur] == j + C[j]) {
ok = 0;
break;
}
}
if (ok)
search(cur + 1);
}
}
}
这里的测试结果是 92,答案正确。
这个程序还可以改进,如下
int total = 0;
int vis[3][N * 2] = {0}; // vis[0] 表示列被占据的情况, vis[1] 表示主对角线(从左上到右下)被占据的情况, vis[2] 表示副对角线被占据的情况
void searchV2(int cur) {
if (cur == n) {
total++;
} else {
for (int i = 0; i < n; i++) {
if (!vis[0][i] && !vis[1][cur + i] && !vis[2][cur - i + n]) { // 利用二维数组直接判断
C[cur] = i;
vis[0][i] = vis[1][cur + i] = vis[2][cur - i + n] = 1; // 修改全局变量
searchV2(cur + 1);
vis[0][i] = vis[1][cur + i] = vis[2][cur - i + n] = 0; // 切记! 一定要改回来
}
}
}
}
关于 vis 数组的说明:它表示已经放置的皇后占据了那些列、主对角线和副对角线。上面的注释也详细说明了这一点。经测试,这个代码跑出来的结果是正确的。
完整代码
#include <iostream>
#include <ctime>
#define N 8
int n = 8;
int tot = 0; // total, 用于记录可能的种数
int C[N] = {-1, -1, -1, -1, -1, -1, -1, -1};
void search(int cur) { // cur 代表当前行
if (cur == n)
tot++; // 递归边界, 只要走到了这里, 所有皇后必然不冲突, 因为这是从第 8 行(也就是最后一行)递归进来的
else {
for (int i = 0; i < n; i++) { // 对列进行遍历
int ok = 1; // 记录当前的摆放位置是否会和之前已经放好的皇后发生冲突
C[cur] = i;
for (int j = 0; j < cur; j++) { // 检查是否和前面的皇后冲突
if (C[cur] == C[j] || cur - C[cur] == j - C[j] || cur + C[cur] == j + C[j]) {
ok = 0;
break;
}
}
if (ok)
search(cur + 1);
}
}
}
int total = 0;
int vis[3][N * 2] = {0}; // vis[0] 表示列被占据的情况, vis[1] 表示主对角线(从左上到右下)被占据的情况, vis[2] 表示副对角线被占据的情况
void searchV2(int cur) {
if (cur == n) {
total++;
} else {
for (int i = 0; i < n; i++) {
if (!vis[0][i] && !vis[1][cur + i] && !vis[2][cur - i + n]) { // 利用二维数组直接判断
C[cur] = i;
vis[0][i] = vis[1][cur + i] = vis[2][cur - i + n] = 1; // 修改全局变量
searchV2(cur + 1);
vis[0][i] = vis[1][cur + i] = vis[2][cur - i + n] = 0; // 切记! 一定要改回来
}
}
}
}
int main() {
clock_t start_time, end_time;
start_time = clock();
for (int i = 0; i < 10000; i++) {
tot = 0;
search(0);
}
end_time = clock();
std::cout<<end_time - start_time<<std::endl;
std::cout<<"一共有"<<tot<<"种解法"<<std::endl;
start_time = clock();
for (int i = 0; i < 10000; i++) {
total = 0;
searchV2(0);
}
end_time = clock();
std::cout<<end_time - start_time<<std::endl;
std::cout<<"一共有"<<total<<"种解法"<<std::endl;
return 0;
}
测试结果:
2897
一共有92种解法
1020
一共有92种解法




