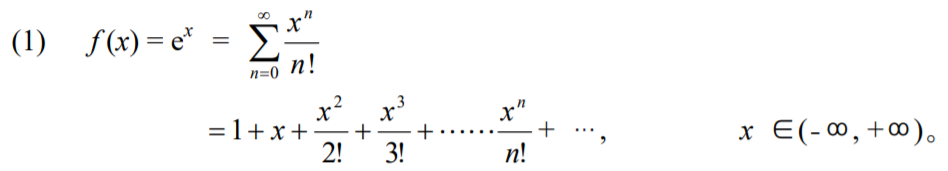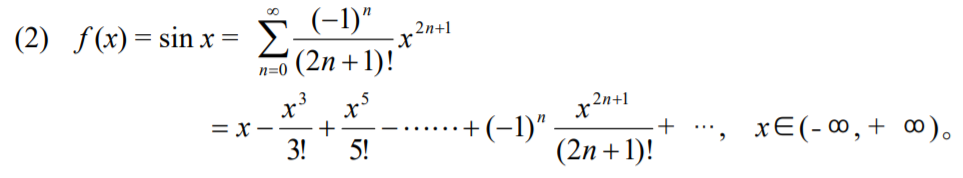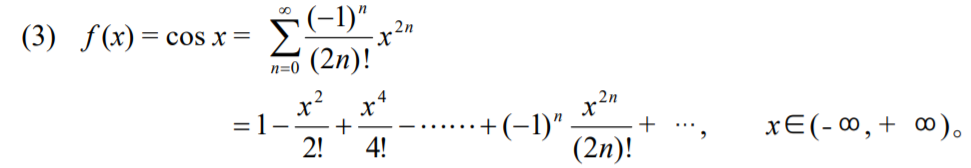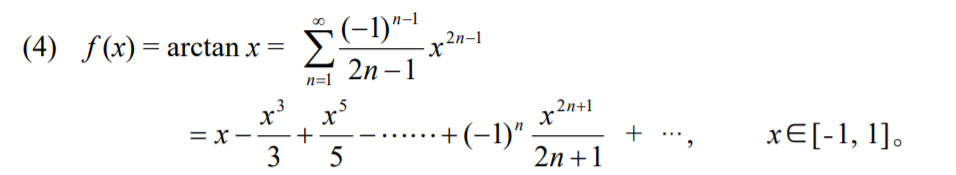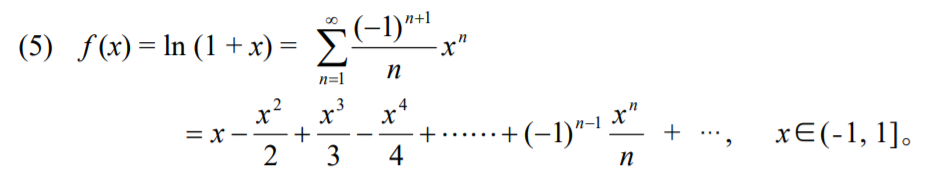一些常用的幂级数展开式
首先回顾一下泰勒展开式: 设函数 \(f(x)\) 在 \(x_0\) 的某个邻域 \(O(x_0, r)\) 中能展开幂级数, 则它的幂级数展开就是 \(f(x)\) 在 \(x_0\) 的 \(Taylor\) 级数:
\[f(x) = \sum_{0}^{\infty}\displaystyle \frac{f^{(n)}(x_0)}{n!}(x - x_0)^n, \quad x \in O(x_0, r).
\]
另外就是一些基本的幂级数展开式:
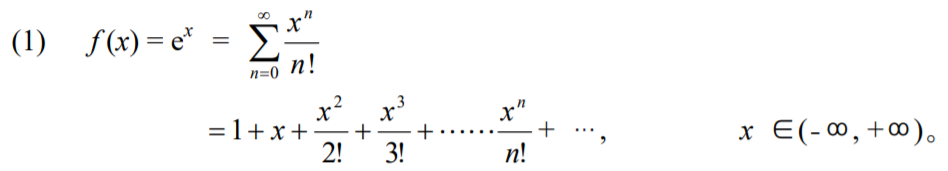
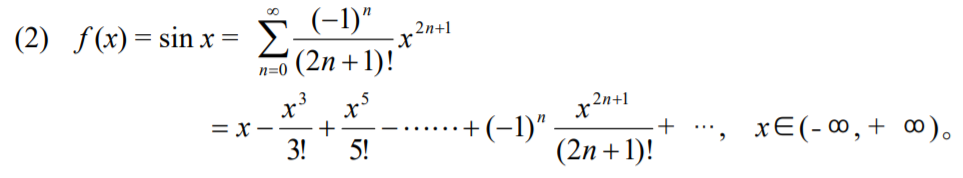
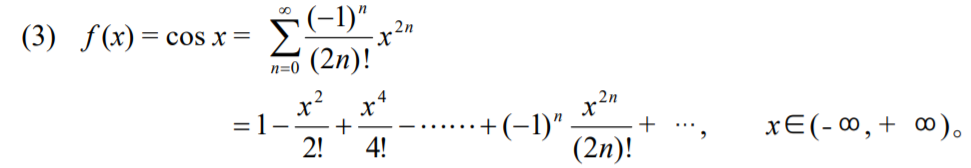
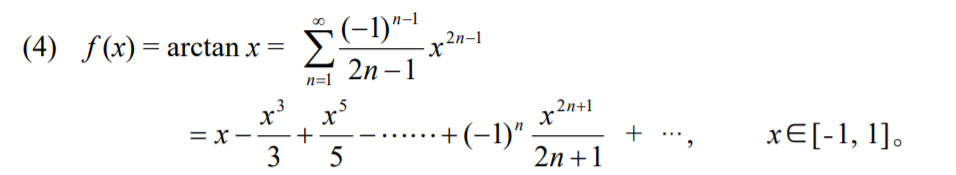
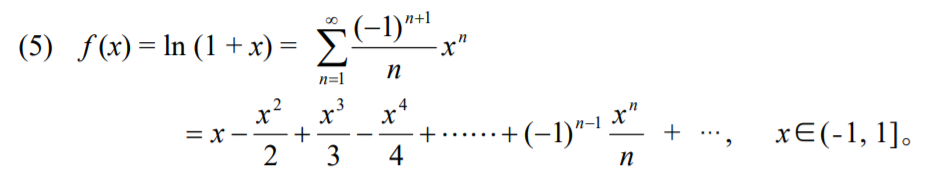

首先回顾一下泰勒展开式: 设函数 \(f(x)\) 在 \(x_0\) 的某个邻域 \(O(x_0, r)\) 中能展开幂级数, 则它的幂级数展开就是 \(f(x)\) 在 \(x_0\) 的 \(Taylor\) 级数:
另外就是一些基本的幂级数展开式: