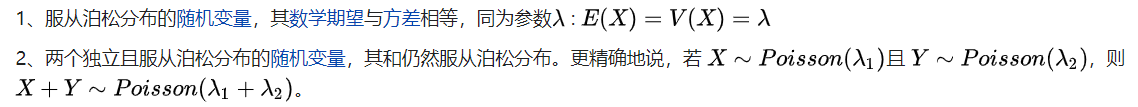泊松分布
定义

泊松分布的期望和方差
期望
\[EX = \lambda
\]
证明 --> 课本 P52 例题
例 4.2 设随机变量 \(X \sim P(\lambda)\), 求 \(EX\).
解
\[EX = \sum_{k = 0}^{\infty}x_kp_k = \sum_{k = 0}^{\infty} k \frac{\lambda ^ k}{k!}e^{-\lambda} = e^{-\lambda}\lambda \sum_{k = 1}^{\infty}\frac{\lambda ^ {k - 1}}{(k - 1)!} = \lambda e^{-\lambda}e^{\lambda } = \lambda
\]
即 \(EX = \lambda\).
模糊计算士按: 上面的计算用到了一个幂级数展开式 -->
\[f(x) = e^x = \sum_{n = 0}^{\infty}\frac{x^n}{n!} = 1 + x + \frac{x^2}{2!} + \frac{x^3}{3!} + ...... \frac{x^n}{n!} + ..., \quad x \in (-\infty, +\infty)
\]
即 -->
\[\sum_{k = 1}^{\infty}\frac{\lambda ^ {k - 1}}{(k - 1)!} = e^\lambda
\]
方差
\[DX = \lambda
\]
证明 --> 课本 P57 例题
例 4.18 设随机变量 \(X \sim P(\lambda)\), 求 \(DX\).
解
\[EX^2 = \sum_{k = 0}^{\infty} k^2 \frac{\lambda ^ k}{k!}e^{-\lambda} = \lambda \sum_{k = 1}^{\infty}ke^{-\lambda}\frac{\lambda ^ {k - 1}}{(k - 1)!} = \lambda\sum_{k = 0}^{\infty} (k + 1) e^{-\lambda}\frac{\lambda ^ k}{k!} = \lambda (\lambda + 1)
\]
则:
\[DX = EX^2 - (EX)^2 = \lambda (\lambda + 1) - \lambda^2 = \lambda.
\]
模糊计算士按: 上面的计算用到了一个幂级数展开式 -->
\[f(x) = e^x = \sum_{n = 0}^{\infty}\frac{x^n}{n!} = 1 + x + \frac{x^2}{2!} + \frac{x^3}{3!} + ...... \frac{x^n}{n!} + ..., \quad x \in (-\infty, +\infty)
\]
将
\[\sum_{k = 0}^{\infty} (k + 1) e^{-\lambda}\frac{\lambda ^ k}{k!}
\]
拆成
\[\sum_{k = 0}^{\infty} ke^{-\lambda}\frac{\lambda ^ k}{k!} + \sum_{k = 0}^{\infty}e^{-\lambda}\frac{\lambda ^ k}{k!}
\]
然后左式可以利用上面的求期望的结果, 右式直接用 \(e^x\) 的幂级数展开就完成了.
泊松分布的重要性质