数据结构实验三 约瑟夫环和多项式乘法问题

一、约瑟夫问题的求解

1、问题描述

N people form a circle, eliminate a person every k people, who is the final survivor?

本次实验内容是用游标方式的循环链表实现对此约瑟夫问题的求解。

2、问题分析与算法设计

• 将人的顺序按照从 1 到 N 的方式进行编号
• 设计节点，将每个人的序号存入相应的节点中
• 构造一个循环链表，将最后一个人的指针指向第一个人，即形成一个环
• 报数，根据条件进行删除，直至人数只剩下一个人时，此时，该节点所存的序号就是最后的幸存者编号

3、实验方案

1. 实现一个用游标实现的循环链表
2. 定义并实现一个可以生成指定节点数的循环链表的函数 CreateList()
3. 定义并实现一个求解约瑟夫问题的函数 JoseSur()，该函数返回最后的幸存者编号
4. 在 main() 函数中进行测试

4、算法实现

/**
 * 求解最后的幸存者编号
 * @param m 间隔的人数
 * @return 幸存者编号
 */
int JosephusRes(int m, List list)
{
    List L = list;

    // 打印循环链表
    // PrintList(L);

    Position prev, tmp;
    int i;

    if (CursorSpace[L].Next == NULL)
    {
        printf("empty list! \n");
        return FAILURE;
    }

    if (CursorSpace[L].Next == CursorSpace[CursorSpace[L].Next].Next)
    {
        printf("survivor is %d \n", CursorSpace[CursorSpace[L].Next].Element);
        return SUCCESS;
    }

    while (!(CursorSpace[L].Next == CursorSpace[CursorSpace[L].Next].Next))
    {
        for (i = 1, tmp = CursorSpace[L].Next, prev = L; i < m; i++) // tmp 初始值为第一个节点(即头节点指向的节点)，prev 初始值为头节点 L
        {
            prev = tmp;
            tmp = CursorSpace[tmp].Next;
        }
        CursorSpace[L].Next = CursorSpace[tmp].Next;
        CursorSpace[prev].Next = CursorSpace[tmp].Next;
        printf("%d is to be deleted \n", CursorSpace[tmp].Element);
        CursorFree(tmp);
    }

    return CursorSpace[CursorSpace[L].Next].Element;
}

5、实验结果

测试用例与实验结果：

a = 8, b = 3

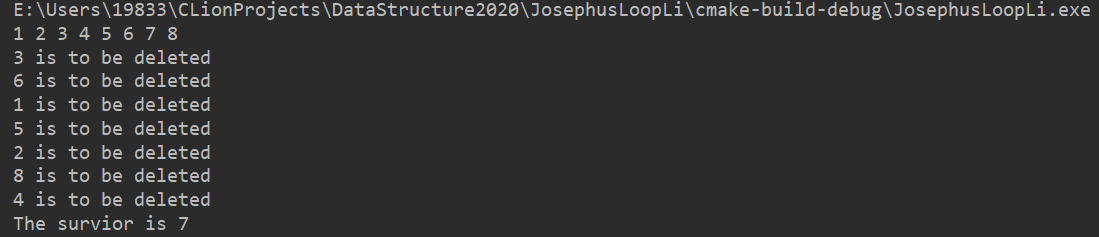
a = 10, b = 2

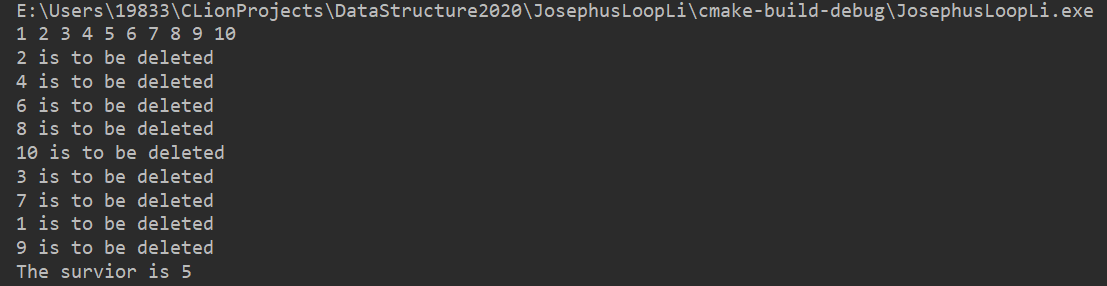
a = 11, b = 3

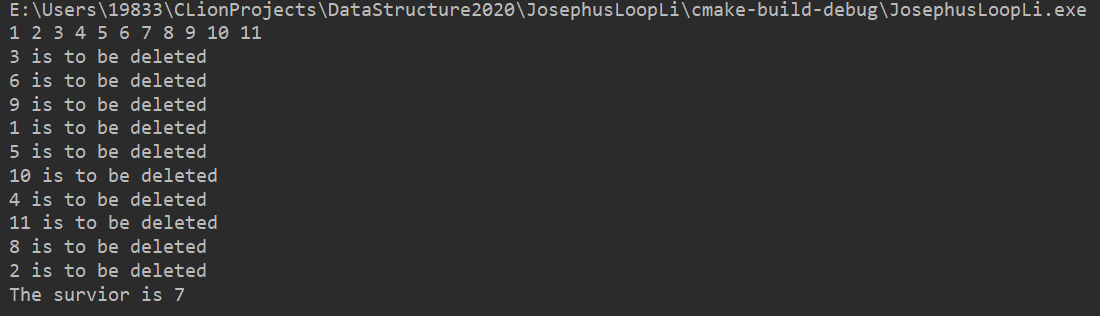
实验结果正确。

6、复杂度分析

容易分析，该算法中主要有一个二重循环，其它的语句执行时间都是常数级别，因此，总体时间复杂度为 \(O(a * b)\)

二、多项式乘法问题

1、问题描述

用链表表示多项式，分别在对指数排序和不排序的情况下，写出两个给定多项式的乘法的函数，并计算其复杂程度。

2、问题分析与算法设计

构造两个链表p1、p2，每个链表节点中存放多项式其中一项的系数和次数，以及下一节点的地址。再构造一个总链表p，代表p1、p2相乘后得到的多项式。总链表每一项的系数为对应p1、p2节点系数之积，每一项的次数为对应p1、p2节点次数之和。用两重循环遍历p1、p2,按照规定的计算方法将相乘所得的指数和次数存入总链表p中。更新总链表时先遍历以及建立的总链表p，看看其中是否以及存在同次项，若存在，更改同次项的系数；若不存在重新开辟一个节点表示该项。

3、代码实现

// 多项式的乘法(sorted)
Polynomial PolyMult(Polynomial P1, Polynomial P2)
{
    Polynomial P, Rear, t1, t2, t;
    int c, e;

    if (!P1 || !P2) return NULL;

    t1 = P1;
    P = (Polynomial)malloc(sizeof(struct PolyNode));
    P->link = NULL;
    while (t1)
    {
        t2 = P2; // 每次循环之后要把 t2 归位到链表的开头
        Rear = P; // 每一次循环都要重新初始化 Rear，使 Rear 的初始值指向链表头
        while (t2)
        {
            c = t1->coef * t2->coef;
            e = t1->expon + t2->expon;
            while (Rear->link && Rear->link->expon > e) // 注意，这里和 e 作比较的是 Rear 的下一个节点中的值
                Rear = Rear->link;
            if (Rear->link && Rear->link->expon == e) {
                if (Rear->link->coef + c)
                    Rear->link->coef += c;
                else { // 系数相加等于 0 的情况，要把该节点删掉
                    t = Rear->link;
                    Rear->link = t->link;
                    free(t);
                }
            } else { // 指数相加啊小于尾节点指数的情况，直接附加到结尾就成
                t = (Polynomial)malloc(sizeof(struct PolyNode));
                t->coef = c;
                t->expon = e;
                t->link = Rear->link;
                Rear->link = t; // 直接将 t2 的值附加到结尾
                Rear = Rear->link;
            }
            t2 = t2->link; // 指针往后移动
        }
        t1 = t1->link;
    }
    t2 = P;
    P = P->link;
    free(t2); // 释放第一个没有存储数据得节点

    return P;
}

// 多项式的乘法(unsorted)
Polynomial PolyMultNotSorted(Polynomial P1, Polynomial P2)
{
    Polynomial P, Rear, t1, t2, t;
    int c, e;

    if (!P1 || !P2) return NULL;

    t1 = P1;
    P = (Polynomial)malloc(sizeof(struct PolyNode));
    P->link = NULL;
    while (t1)
    {
        t2 = P2; // 每次循环之后要把 t2 归位到链表的开头
        Rear = P; // 每一次循环都要重新初始化 Rear，使 Rear 的初始值指向链表头
        while (t2)
        {
            c = t1->coef * t2->coef;
            e = t1->expon + t2->expon;

            if (!P->link || e > P->link->expon) {
                t = (Polynomial)malloc(sizeof(struct PolyNode));
                t->coef = c;
                t->expon = e;
                t->link = P->link;
                P->link = t; // 在表头插入
            } else {
                while (Rear->link && Rear->link->expon > e) // 注意，这里和 e 作比较的是 Rear 的下一个节点中的值
                    Rear = Rear->link;
                if (Rear->link && Rear->link->expon == e) {
                    if (Rear->link->coef + c)
                        Rear->link->coef += c;
                    else { // 系数相加等于 0 的情况，要把该节点删掉
                        t = Rear->link;
                        Rear->link = t->link;
                        free(t);
                    }
                } else { // 指数相加啊小于尾节点指数的情况，直接附加到结尾就成
                    t = (Polynomial)malloc(sizeof(struct PolyNode));
                    t->coef = c;
                    t->expon = e;
                    t->link = Rear->link;
                    Rear->link = t; // 直接将 t2 的值附加到结尾
                    Rear = Rear->link;
                }
            }
                t2 = t2->link; // 指针往后移动
                Rear = P;
        }
        t1 = t1->link;
    }
    t2 = P;
    P = P->link;
    free(t2); // 释放第一个没有存储数据得节点

    return P;
}

4、实验结果

测试用例及运行结果：

sorted：

• Poly1: \(3x^5 + 4x^4 + (-1)x^3 + 2x\)
• Poly2: \(2x^4 + x^3 + (-7)x^2 + x\)

unsorted：

• Poly1: \(4x^4 + (-1)x^3 + 3x^5 + 2x\)
• Poly2: \(2x^4 + (-7)x^2 + x^3 + x\)

结果正确

5、时间复杂度分析

不妨假设两个相乘的多项式的项数都是 \(n\)，在排序的情况下，我们可以得到这样一个递推的公式：\(T(n) = T(n - 1) + O(n)\)，因此其时间复杂度为 \(O(n^2)\)；对于未排序的情况，算法在第二层循环里每一次都要重新对 Rear 进行归位到头节点的操作，因此，可以得到递推公式：\(T(n) = T(n - 1) + O(n^2)\)，因此，其时间复杂度为 \(O(n^3)\)

附：完整代码

1. 约瑟夫问题代码

Josephus.h

typedef int ElementType;
#define SpaceSize 100 // 内存的最大值
#define SUCCESS 0
#define FAILURE -1

#ifndef JOSEPHUSLOOPLI_JOSHPHUS_H
#define JOSEPHUSLOOPLI_JOSHPHUS_H

typedef int PtrToNode;
typedef PtrToNode List;
typedef PtrToNode Position;

void InitializeCursorSpace( void );

List MakeEmpty( List L );
int IsEmpty( const List L );
int IsLast( const Position P, const List L );
Position Find( ElementType X, const List L );
void Delete( ElementType X, List L );
Position FindPrevious( ElementType X, const List L );
void Insert( ElementType X, List L, Position P );
void DeleteList( List L );
Position Header( const List L );
Position First( const List L );
Position Advance( const Position P );
ElementType Retrieve( const Position P );
List CreateList(int n);
int JosephusRes(int m, List list);
void PrintList(const List L);

#endif //JOSEPHUSLOOPLI_JOSHPHUS_H

Josephus.c

#include "Josephus.h"
#include <stdlib.h>
#include "fatal.h"

// 元素的结构体
struct Node
{
    ElementType Element; // int
    Position Next; // PtrToNode
};

struct Node CursorSpace[SpaceSize]; // SpaceSize 100

static Position
CursorAlloc(void) // 从下面可以推断出，这里是分配空间给新的元素，并且取内存的地方是下面初始化的那块有100个元素大小的区域
{
    Position P; // 这里的Position是int类型的别名

    P = CursorSpace[0].Next; // 最开始时这里是1，也就是第一次取出的内存是0后面的那一块
    CursorSpace[0].Next = CursorSpace[P].Next; // 然后管理内存的头节点就要往后挪一位，当所有的内存被分配完了之后，CursorSpace[ 0 ]会指向它自身，即其Next值为0

    return P; // 返回取出的那一块内存
}

// 释放一个节点的内存
static void
CursorFree(Position P) // P就代表了索引，根据这个索引可以找到其元素
{
    // 下面这两行代码就是根据内存的头节点0，将归还的内存放到freelist的最前面
    CursorSpace[P].Next = CursorSpace[0].Next;
    CursorSpace[0].Next = P; // 释放并归还内存，从放到CursorSpace[0]这一处可以看出，但是问题是如何使用这块归还的内存是一个问题，有一点模糊！！！--> 在测试函数中添加了几个测试部分，分析内存的摆放情况之后就清晰多了！
}

// cursorSpace的初始化
// 这里相当于是取出一块内存，所以并没有往里面存数据
// cursorSpace数组里面存放的是Node节点，里面有Element和Next两个成员
// 这里只是初始化Next这一个成员，取内存的时候则是根据数组的索引来
void
InitializeCursorSpace(void)
{
    int i;

    for (i = 0; i < SpaceSize; i++)
        CursorSpace[i].Next = i + 1;
    CursorSpace[SpaceSize - 1].Next = 0;
}

List
MakeEmpty(List L)
{
    if (L)
        DeleteList(L);
    L = CursorAlloc();
    if (L == 0)
        FatalError("Out of memory!");
    CursorSpace[L].Next = 0; // 空链表的头节点指向0，同样指向0的还有内存的最后一块，还有非空链表的最后一个元素
    return L;
}

/* Return true if L is empty */
// 判断链表是否为空，判断的方法是看链表的头节点是否指向0
int
IsEmpty(List L)
{
    return CursorSpace[L].Next == 0;
}

/* Return true if P is the last position in list L */
/* Parameter L is unused in this implementation */
// 判断是否到了表的尽头
int IsLast(Position P, List L)
{
    return CursorSpace[P].Next == CursorSpace[L].Next; // Next指向了0代表遍历到了表的尽头
}

/* Return Position of X in L; 0 if not found */
/* Uses a header node */
// 返回表L中的X的位置
Position
Find(ElementType X, List L)
{
    Position P;

      P = CursorSpace[L].Next;
      while (P && CursorSpace[P].Element != X)
          P = CursorSpace[P].Next;

      return P; // 返回的Position P有何用处？其用处就是作为索引，它本身也是通过上一个元素的Next找到的
}

/* Assume that the position is legal */
/* Assume use of a header node */
void
Delete(ElementType X, List L)
{
    Position P, TmpCell;

    P = FindPrevious(X, L);

    if (!IsLast(P, L))  /* Assumption of header use */
    {                      /* X is found; delete it */
        TmpCell = CursorSpace[P].Next;
        CursorSpace[P].Next = CursorSpace[TmpCell].Next;
        CursorFree(TmpCell); // 删除，和普通的链表类似，这里释放内存的方式有些区别
    }
}


/* If X is not found, then Next field of returned value is 0 */
/* Assumes a header */

Position
FindPrevious(ElementType X, List L) // 这里根据ElementType来找前一个元素，那么，如果有重复的现象，那么就返回第一次找到的结果
{
    Position P;

     P = L;
     while (CursorSpace[P].Next &&
            CursorSpace[CursorSpace[P].Next].Element != X)
         P = CursorSpace[P].Next;

     return P;
}


/* Insert (after legal position P) */
/* Header implementation assumed */
/* Parameter L is unused in this implementation */
/**
 * 插入操作
 * @param X 要插入的元素值
 * @param L 表的头节点
 * @param P 表示现存的表中的一个节点的位置，这里就是将新插入的值插在P的后面
 */
void
Insert(ElementType X, List L, Position P)
{
    Position TmpCell;

    // 先取出一块内存，也就是分配空间
      TmpCell = CursorAlloc();
      if (TmpCell == 0) // 如果TemCell为0，则意味着当初分配的空间为SpaceSize用到了尽头
          FatalError("Out of space!!!");

      CursorSpace[TmpCell].Element = X;
      CursorSpace[TmpCell].Next = CursorSpace[P].Next;
      CursorSpace[P].Next = TmpCell;
}



/* Correct DeleteList algorithm */
// 删除整个表，删除之后头节点变成了空头，头节点里本身的Element的是是没有赋的
void
DeleteList(List L)
{
    Position P, Tmp;

      P = CursorSpace[L].Next;  /* Header assumed */ // 先将第一个节点取出来
      CursorSpace[L].Next = 0; // 然后将链表头归零
    // 循环，把整个表给删除
      while (P != 0)
    {
          Tmp = CursorSpace[P].Next; // 这里并没有把Element给清零，虽然最后并没有什么影响
          CursorFree(P);
          P = Tmp;
    }
}

// 返回头节点，即L这个节点本身
Position
Header(List L)
{
    return L;
}

// 返回第一个节点，即头节点指向的第一个节点
Position
First(List L)
{
    return CursorSpace[L].Next;
}

// 相当于指针往后移动一位
Position
Advance(Position P) // 这里P是任意节点，这个函数的作用就是取出节点的下一个节点，相当于游标往后移动一位，例如，P是L的情况下，CursorSpace[ P ].Next就是取出第一个元素的Position
{
    return CursorSpace[P].Next;
}

// 取出数据
ElementType
Retrieve(Position P)
{
    return CursorSpace[P].Element;
}

List CreateList(int n)
{
    List L; // List如果只是声明而不赋值就是NULL
    /*if (L == NULL)
    {
        printf("List为空\n");
    }*/
    Position P;
    int i;

    InitializeCursorSpace(); // 初始化内存池
    L = MakeEmpty(NULL); // 不传参也代表NULL
    P = Header(L);

    for (i = 1; i <= n; i++)
    {
        Insert(i, L, P); // L是头节点
        P = Advance(P);
    }

    CursorSpace[P].Next = CursorSpace[L].Next;

    return L;
}


/**
 * 求解最后的幸存者编号
 * @param m 间隔的人数
 * @return 幸存者编号
 */
int JosephusRes(int m, List list)
{
    List L = list;

    // 打印循环链表
    // PrintList(L);

    Position prev, tmp;
    int i;

    if (CursorSpace[L].Next == NULL)
    {
        printf("empty list! \n");
        return FAILURE;
    }

    if (CursorSpace[L].Next == CursorSpace[CursorSpace[L].Next].Next)
    {
        printf("survivor is %d \n", CursorSpace[CursorSpace[L].Next].Element);
        return SUCCESS;
    }

    while (!(CursorSpace[L].Next == CursorSpace[CursorSpace[L].Next].Next))
    {
        for (i = 1, tmp = CursorSpace[L].Next, prev = L; i < m; i++) // tmp 初始值为第一个节点(即头节点指向的节点)，prev 初始值为头节点 L
        {
            prev = tmp;
            tmp = CursorSpace[tmp].Next;
        }
        CursorSpace[L].Next = CursorSpace[tmp].Next;
        CursorSpace[prev].Next = CursorSpace[tmp].Next;
        printf("%d is to be deleted \n", CursorSpace[tmp].Element);
        CursorFree(tmp);
    }

    return CursorSpace[CursorSpace[L].Next].Element;
}

// 打印表
void
PrintList(const List L)
{
    Position P = Header(L);

    if (IsEmpty(L))
        printf("Empty list\n");
    else
    {
        do
        {
            P = Advance(P);
            printf("%d ", Retrieve(P));
        } while (!IsLast(P, L));
        printf("\n");
    }
}

main.c

#include <stdio.h>
#include "Josephus.h"

int main()
{
    List list = CreateList(8); // 创建一个大小为 n 的循环链表

    // 打印生成的链表
    PrintList(list);

    int res = JosephusRes(3, list);

    printf("The survior is %d \n", res);
    return 0;
}

fatal.h

#include <stdio.h>
#include <stdlib.h>

#define Error( Str )        FatalError( Str )
#define FatalError( Str )   fprintf( stderr, "%s\n", Str ), exit( 1 )

多项式相乘问题

Poly.h

#ifndef POLYNOMIALCOMPUTE_POLY_H
#define POLYNOMIALCOMPUTE_POLY_H

struct PolyNode;
typedef struct PolyNode *Polynomial;

void Attach(int c, int e, Polynomial *pRear);
Polynomial PolyMult(Polynomial P1, Polynomial P2);
Polynomial PolyMultNotSorted(Polynomial P1, Polynomial P2);
Polynomial ReadPoly();
void PrintPoly(Polynomial P);
Polynomial ReadPolyFromArray(int a[], int n);

#endif //POLYNOMIALCOMPUTE_POLY_H

Poly.c

#include "poly.h"
#include <malloc.h>
#include <stdlib.h>
#include <stdio.h>

struct PolyNode {
    Polynomial link; // 指向下一个节点的位置
    int expon; // 指数，英文是 exponent
    int coef; // 系数，英文是 coefficient
};

// 新增一个节点
void Attach(int c, int e, Polynomial *pRear)
{
    Polynomial P;

    P = (Polynomial)malloc(sizeof(struct PolyNode)); // 分配空间
    P->coef = c; // 对新节点赋值
    P->expon = e;
    P->link = NULL;
    (*pRear)->link = P; // 尾节点指向P
    *pRear = P; // 修改 pRear 值
}

// 多项式的乘法(sorted)
Polynomial PolyMult(Polynomial P1, Polynomial P2)
{
    Polynomial P, Rear, t1, t2, t;
    int c, e;

    if (!P1 || !P2) return NULL;

    t1 = P1;
    P = (Polynomial)malloc(sizeof(struct PolyNode));
    P->link = NULL;
    while (t1)
    {
        t2 = P2; // 每次循环之后要把 t2 归位到链表的开头
        Rear = P; // 每一次循环都要重新初始化 Rear，使 Rear 的初始值指向链表头
        while (t2)
        {
            c = t1->coef * t2->coef;
            e = t1->expon + t2->expon;
            while (Rear->link && Rear->link->expon > e) // 注意，这里和 e 作比较的是 Rear 的下一个节点中的值，这样下面的插入操作才解释得通
                Rear = Rear->link;
            if (Rear->link && Rear->link->expon == e) {
                if (Rear->link->coef + c)
                    Rear->link->coef += c;
                else { // 系数相加等于 0 的情况，要把该节点删掉
                    t = Rear->link;
                    Rear->link = t->link;
                    free(t);
                }
            } else { // 指数相加啊小于尾节点指数的情况，直接附加到结尾就成
                t = (Polynomial)malloc(sizeof(struct PolyNode));
                t->coef = c;
                t->expon = e;
                t->link = Rear->link;
                Rear->link = t; // 直接将 t2 的值附加到结尾
                Rear = Rear->link;
            }
            t2 = t2->link; // 指针往后移动
        }
        t1 = t1->link;
    }
    t2 = P;
    P = P->link;
    free(t2); // 释放第一个没有存储数据得节点

    return P;
}

// 多项式的乘法(unsorted)
Polynomial PolyMultNotSorted(Polynomial P1, Polynomial P2)
{
    Polynomial P, Rear, t1, t2, t;
    int c, e;

    if (!P1 || !P2) return NULL;

    t1 = P1;
    P = (Polynomial)malloc(sizeof(struct PolyNode));
    P->link = NULL;
    while (t1)
    {
        t2 = P2; // 每次循环之后要把 t2 归位到链表的开头
        Rear = P; // 每一次循环都要重新初始化 Rear，使 Rear 的初始值指向链表头
        while (t2)
        {
            c = t1->coef * t2->coef;
            e = t1->expon + t2->expon;

            if (!P->link || e > P->link->expon) {
                t = (Polynomial)malloc(sizeof(struct PolyNode));
                t->coef = c;
                t->expon = e;
                t->link = P->link;
                P->link = t; // 在表头插入
            } else {
                while (Rear->link && Rear->link->expon > e) // 注意，这里和 e 作比较的是 Rear 的下一个节点中的值，这样下面的插入操作才解释得通
                    Rear = Rear->link;
                if (Rear->link && Rear->link->expon == e) {
                    if (Rear->link->coef + c)
                        Rear->link->coef += c;
                    else { // 系数相加等于 0 的情况，要把该节点删掉
                        t = Rear->link;
                        Rear->link = t->link;
                        free(t);
                    }
                } else { // 指数相加啊小于尾节点指数的情况，直接附加到结尾就成
                    t = (Polynomial)malloc(sizeof(struct PolyNode));
                    t->coef = c;
                    t->expon = e;
                    t->link = Rear->link;
                    Rear->link = t; // 直接将 t2 的值附加到结尾
                    Rear = Rear->link;
                }
            }
                t2 = t2->link; // 指针往后移动
                Rear = P;
        }
        t1 = t1->link;
    }
    t2 = P;
    P = P->link;
    free(t2); // 释放第一个没有存储数据得节点

    return P;
}

// 输出多项式
void PrintPoly(Polynomial P)
{
    int flag = 0; // 辅助调整输出格式用

    if (!P) {
        printf("0 0\n");
        return;
    }

    while (P) {
        if (!flag)
            flag = 1;
        else
            printf(" 🔺 ");
        printf("%d %d", P->coef, P->expon);
        P = P->link;
    }
    printf("\n");
}

// 读入多项式-->控制台输入
Polynomial ReadPoly()
{
    Polynomial P, Rear, t;
    int c, e, N;

    scanf("%d", &N);
    P = (Polynomial)malloc(sizeof(struct PolyNode)); // 链表头空姐点
    P->link = NULL;
    Rear = P; // 复制 P 到 Rear，这样就可以不修改 P
    while (N--) {
        scanf("%d %d", &c, &e);
        Attach(c, e, &Rear); // 将当前项插入多项式尾部
    }
    t = P;
    P = P->link;
    free(t); // 删除临时生成头节点（因为里面也没存储数据）
    return P;
}

// 从数组读入多项式
/**
 *
 * @param a 多项式数组
 * @param n 多项式的项数
 * @return
 */
Polynomial ReadPolyFromArray(int a[], int n)
{
    Polynomial P, Rear, t;
    int c, e;

    P = (Polynomial)malloc(sizeof(struct PolyNode)); // 链表头空姐点
    P->link = NULL;
    Rear = P; // 复制 P 到 Rear，这样就可以不修改 P
    for (int i = 0, j = 0; i < n; i++)
    {
        c = a[j];
        e = a[j + 1];
        Attach(c, e, &Rear);
        j += 2;
    }
    t = P;
    P = P->link;
    free(t); // 删除临时生成头节点（因为里面也没存储数据）
    return P;
}

main.c

#include "poly.h"

// 测试函数
int main()
{
    // 测试数据
    int a1[4 * 2] = {3, 5, 4, 4, -1, 3, 2, 1};
    int b1[4 * 2] = {2, 4, 1, 3, -7, 2, 1, 1};

    int a2[4 * 2] = { 4, 4, -1, 3, 3, 5, 2, 1};
    int b2[4 * 2] = {2, 4, -7, 2, 1, 3, 1, 1};

    Polynomial P1, P2, PP; // PP 表示多项式乘积 Product

    P1 = ReadPolyFromArray(a2, 4);
    PrintPoly(P1);
    P2 = ReadPolyFromArray(b2, 4);
    PrintPoly(P2);

    PP = PolyMultNotSorted(P1, P2);
    PrintPoly(PP);

    return 0;
}